A rectangular cake is transported via a truck to a restaurant. On the way to the destination, the truck hits a pothole, which shatters the cake in $N$ perfectly rectangular pieces of width $w_i$ and length $l_i$, for $1 \le i \le N$.

At the destination, the damage is assessed, and the customer decides to order a replacement cake of the same dimensions. Unfortunately, the original order form was incompletely filled and only the width $W$ of the cake is known. The restaurant asks for your help to find out the length $L$ of the cake.

Fortunately, all pieces of the cake have been kept.

Input🔗

The input consists of the following integers:

• on the first line, the width $W$ of the cake;
• on the second line, the number $N$ of shattered pieces;
• on each of the next $N$ lines, the width $w_i$ and length $l_i$ of each piece.

$1 \le N \le 5000000$ $1 \le W, L \le 10000$ $1 \le w_i, l_i \le 10000$

Output🔗

The output should be the integer $L$.

Sample Input🔗

4
7
2 3
1 4
1 2
1 2
2 2
2 2
2 1

Sample Output🔗

6

Spike is a bounty hunter and he is currently tracking a criminal! To investigate he uses his spaceship, the Swordfish II, and travels to $N$ different places on 2D Euclidean space before returning to his crew at the starting location with all the information he has gathered. The starting location is the leftmost place (with the lowest $x$-coordinate) and Spike wants to travel to every other place before returning. However space fuel costs a lot of Woolongs and Spike would rather spend his money on special beef with bell peppers. Therefore he wants to travel the minimum possible distance.

On top of that he is being chased by the Red Dragon crime syndicate. To make sure they don’t catch him he can only visit places in increasing order of their $x$-coordinate until he reaches the rightmost place (with the largest $x$-coordinate), then he can turn around and visit places in decreasing order of their $x$-coordinate until he reaches his starting location again.

Input🔗

The input starts with an integer $T$ ($1 \le T \le 100$) specifying the number of test cases that follow.

Each test case consists of an integer $N$ ($2 \le N \le 512$) specifying the number of places in the tour. The coordinates of these places are given as integers in the next $N$ lines, $x$-coordinate first, $y$-coordinate second ($0 \le x, y \le 5000$). The places are given in ascending order of the $x$-coordinate.

Every place has a unique $x$-coordinate.

Output🔗

For each test case, output on a single line the minimum travel distance needed to complete the tour. Your output should have an absolute or relative error of at most $10^{-2}$.

Sample Input🔗

2
5
0 1
1 2
2 0
3 2
4 1
3
100 1
200 1
300 1

Sample Output🔗

9.300563079746
400

To guard the art jewelry exhibition at night, the security agency has decided to use a new laser beam system, consisting of sender-receiver pairs. Each pair generates a strip of light of one unit width and guards all objects located inside the strip. Your task is to help the agency and to compute for each exhibition room the minimum number of sender-receiver pairs which are sufficient to protect all exhibits inside the room.

Any room has a rectangle shape, so we describe it as an $[0, N] × [0, M]$ rectangle in the plane. The objects we need to guard are represented as points inside that rectangle. Each sender is mounted on a wall and the corresponding receiver on the opposite wall in such a way that the generated strip is a rectangle of unit width and length either $N$ or $M$. Since the new laser beam system is still not perfect, each sender-receiver pair can only be mounted to generate strips the corners of which have integer coordinates. An additional drawback is that the sender-receiver pairs can protect only items inside the strips, but not those lying on their borders. Thus, the security agency arranged the exhibits in such a way that both coordinates of any point representing an exhibit are non-integers.

The figure below (left) illustrates eight items arranged in $[0, 4] × [0, 4]$ (the second sample input). In the room, up to eight sender-receiver pairs can be mounted. The figure to the right shows an area protected by three sender-receiver pairs.

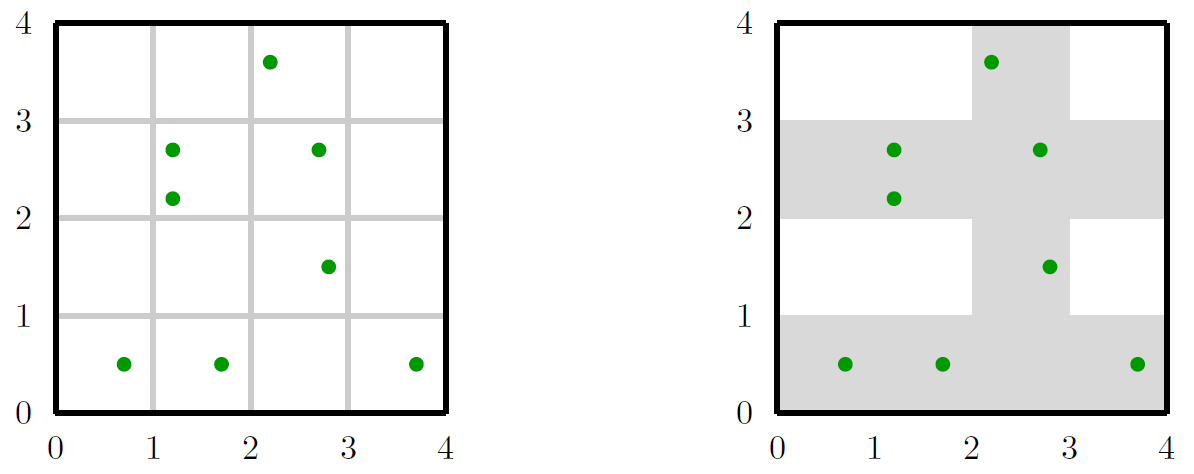
Input🔗

The input starts with the number of exhibition rooms $R \le 10$. Then the descriptions of the $R$ rooms follow. A single description starts with a single line, containing three integers: $0 < N \le 100$, $0 < M \le 100$, specifying the size of the current room and $0 < K \le 104$, for the number of exhibits.

Next $K$ lines follow, each of which consists of two real numbers $x, y$ describing the exhibit coordinates. You can assume that $0 < x < N$, $0 < y < M$ and that $x$ and $y$ are non-integer.

Output🔗

For every room output one line containing one integer, that is the minimum number of sender-receiver pairs sufficient to protect all exhibits inside the room.

Sample Input🔗

2
1 5 3
0.2 1.5
0.3 4.8
0.4 3.5
4 4 8
0.7 0.5
1.7 0.5
2.8 1.5
3.7 0.5
2.2 3.6
2.7 2.7
1.2 2.2
1.2 2.7

Sample Output🔗

1
3

Gunnar and Emma play a lot of board games at home, so they own many dice that are not normal 6-sided dice. For example they own a die that has $10$ sides with numbers $47, 48, ..., 56$ on it.

There has been a big storm in Stockholm, so Gunnar and Emma have been stuck at home without electricity for a couple of hours. They have finished playing all the games they have, so they came up with a new one.

Each player has $2$ dice which he or she rolls. The player with a bigger sum wins. If both sums are the same, the game ends in a tie.

Given the description of Gunnar’s and Emma’s dice, which player has higher chances of winning?

All of their dice have the following property: each die contains numbers $a, a + 1, ..., b$, where $a$ and $b$ are the lowest and highest numbers respectively on the die. Each number appears exactly on one side, so the die has $b - a + 1$ sides.

Input🔗

The first line contains four integers $a_1, b_1, a_2, b_2$ that describe Gunnar’s dice. Dice number $i$ contains numbers $a_i, a_i + 1, ..., b_i$ on its sides. You may assume that $1 \le ai \le bi \le 100$ . You can further assume that each die has at least four sides, so $a_i + 3 \le b_i$ .

The second line contains the description of Emma’s dice in the same format.

Output🔗

Output the name of the player that has higher probability of winning. Output "Tie" if both players have same probability of winning.

Sample Input 1🔗

1 4 1 4
1 6 1 6

Sample Output 1🔗

Emma

Sample Input 2🔗

1 8 1 8
1 10 2 5

Sample Output 2🔗

Tie

Sample Input 3🔗

2 5 2 7
1 5 2 5

Sample Output 3🔗

Gunnar

Per is repairing roads. The job is concentrated on roads with one lane in each direction. Thus, when Per closes down the lane in one direction, all traffic has to go through the other lane. This is done by allowing only one direction of travel at any time. Per is often assigned the task of directing the traffic through this lane.

No car drives before being given a “go” signal from Per, and all the cars drive through the maintained segment at the same speed. Because there is only one lane, cars in one direction must leave the segment before cars in the other direction can enter. For safety reasons, cars driving in the same direction have to keep a distance of at least $3$ seconds between each other.

For example, if cars $A$ and $B$ arrive at the west endpoint at second $10$, Per can let them go at earliest second $10$ and $13$ in the order they arrived. If it, in this example, takes $8$ seconds to pass and car $C$ arrives at the east endpoint at second $17$, then car $C$ has to wait $4$ seconds until Per lets it go at second $21$.

There is a problem of drivers getting irritated with Per; they think they have to stop for too long. Per has been logging how long they can bear to wait before they get irritated. One day, to be able to evaluate his work, Per noted down when the cars arrived at the two endpoints of the segment. Per’s question is the following: what is the least number of drivers that can be irritated? We assume that a driver gets irritated if the time between the moment he arrives at the maintained segment and the moment he is actually given the “go” exceeds his irritation time limit.

Input🔗

The first line of the input contains two integers $t$ and $n$ ($4 \le t \le 180, 1 \le n \le 250$), where $t$ is the time in seconds needed for a car to pass the segment under maintenance, and $n$ is the total number of cars arriving at the segment. The following $n$ lines describe the cars. The $i$-th line contains the description of the $i$-th car in the following format:

• one character $d$, being $W$ for cars arriving at the west endpoint of the segment, and $E$ for the ones that arrive at the east endpoint;
• two integers $a$ and $r$ ($0 \le a < 86 400, 0 \le r \le 3 600$), where $a$ denotes the arrival time in seconds after midnight, and $r$ denotes the time in seconds it takes for the driver to get irritated.

The cars arrive in the order specified in the input and they cannot overtake each other. In particular, a car whose driver is already irritated has to stay in the queue until eventually receiving the “go” and passing the maintained segment.

Output🔗

Output one line with the least possible number of irritated drivers.

Sample Input 1🔗

8 3
W 10 0
W 10 3
E 17 4

Sample Output 1🔗

0

Sample Input 2🔗

100 5
W 0 200
W 5 201
E 95 1111
E 95 1
E 95 11

Sample Output 2🔗

1

André Claude Marzipan is the head chef at the French restaurant Le Chaud Chien. He owns a vast number of baking trays, which come in two sizes: $1$ foot by $1$ foot, and $1$ foot by $2$ feet. He stores them along $3$-foot deep shelves of various lengths. For example, on a shelf that is $5$ feet long, he might store baking trays in either of the two ways shown below:

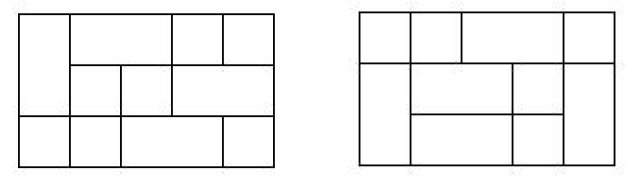
Of course, there are many more than just these two ways, and in his off hours André often wonders how many different ways he can place trays on a given shelf. André is a bit of un maniaque du rangement (neat freak), so he insists that the trays are always aligned along the two axes defined by the shelf edges, that the edges of the trays are always $1$ foot multiples away from any edge, and that no portion of a tray extends beyond the shelf. The matter is complicated by the fact that often there are locations on the shelf where he does not want to put any baking trays, due to leaks above the shelf, dents in the shelf’s surface, etc. Since André is more adept at cuisine than counting, he needs a little help.

Input🔗

The input consists of two lines: the first line will contain two integers $m, n$, where $1 \le m \le 24$ indicates the length of the shelf (which is always $3$-feet deep) and $n$ indicates the number of bad locations on the shelf. The next line will contain $n$ coordinate pairs $x y$ indicating the locations where trays should not be placed, where $0 < x < m$ and $0 < y < 3$. No location will have integer coordinates and coordinates are specified to the nearest hundredth. If $n = 0$, this second line will be blank.

Output🔗

Output the number of ways that trays could be placed on the shelf.

Sample Input 1🔗

4 0

Sample Output 1🔗

823

Sample Input 2🔗

4 2
0.29 2.44 2.73 1.8

Sample Output 2🔗

149

In the wizarding world of security, there are two kinds of researcher: the idealist arranging hat and the mercenary deranging hat.

As we learned last year, an arranging hat carefully sorts out any list of letters given to it into ascending order. However, a deranging hat performs the exact opposite function: putting a sorted string of letters back into its original order.

The tool of choice for today’s discerning headwear is a sorting network: a sequence of instructions represented by a list of pairs of numbers $A_i$ and $B_i$, meaning that if at step $i$ the $A$-th item in the string is not already smaller than the $B$-th item, they should be swapped immediately.

Given a specific word $W$, output a sorting network that the deranging hat can use to form the word from its original sorted letters.

Input🔗

One line containing one string of lowercase Latin letters (‘a’-‘z’), $S$, containing at most $1000$ characters.

Output🔗

Output at most 10000 lines, each containing two integers $A_i$ and $B_i$ ($1 \le A_i, B_i \le |S|$ ) giving the $i$-th operation to perform.

Sample Input 1🔗

bab

Sample Output 1🔗

2 1

Sample Input 2🔗

dude

Sample Output 2🔗

4 3
3 2

Times are hard at the Association of Chartered Mountaineers.

The growth of their pedestrian sport has slowed to a crawl. Instead of taking up mountaineering, younger potentials are gravitating towards warmer indoor activities such as snooker, musical chairs, and programming contests.

To win over more members, the Association is going to organise a series of new time trial orienteering events next year. The route for the first race will be a short run through the Cairngorms, with every contestant following the same route designated by marker points but all starting at different times.

Because hiking can be dangerous, and many of the contestants will be inexperienced, the competition committee drew up two rules:

• Every contestant needs to keep a specific maximum distance away from the next-closest contestant, in either direction, at all times.
• Every contestant should be given personal space. If a contestant needs a personal space of $D$ metres, nobody else should ever come closer than that at any time. This distance varies according to level of experience.

The hardest part of orienteering is the pathfinding; once a contestant knows where to go next, they can get there in almost no time (for the purposes of this problem, instantaneously).

In fact, while the inaugural ACM "Icy-Cold Peak Contest" is already underway, pathfinding is turning out to be a problem: nobody is sure whether they can move next without breaking any of the conditions on minimum and maximum distance.

Help the runners reach the end of their route by computing a list of who should move to the next goal point, and at what time.

Input🔗

• One line containing an integer $B$ ($1 \le B \le 50000$), the maximum separation allowed between any two runners.
• One line containing an integer $P$ ($3 \le P \le 1000$), the number of marker points along the route.
• One line containing $P$ unique space-separated integers $d_1 ... d_P$ ($0 \le d_i \le 10^6$), with $d_i$ being the distance of the $i$-th vertex from the starting point $d_1 = 0$.
• One line containing an integer $K$ ($2 \le K \le 1000$), the number of hikers on the landscape.
• $K$ further lines, each containing the pair of space-separated integers $A_i$ and $V_i$ ($1 \le A_i \le 10^6; 1 \le V_i \le P$), the minimum separation distance and current marker position respectively for the $i$-th person.

The initial configuration of hikers will be legal according to the minimum and maximum distance rules. The hikers will be given in increasing order of distance from the start.

Output🔗

If it is not possible to get everyone to the end of the route without breaking minimum or maximum distance requirements, output impossible.

Otherwise, output a space-separated list of moves on one line, each describing which person should make the next move.

If anyone falls off the landscape, your answer will not be judged as correct. However, once someone has arrived at the end of their journey they cease to count towards any rule violations.

Sample Input 1🔗

3
8
0 1 2 3 4 5 6 7
2
2 1
2 4

Sample Output 1🔗

1 2 1 2 1 2 1 2 1 1 1

Sample Input 2🔗

10
10
0 1 3 6 10 14 17 19 20 21
3
3 1
1 3
3 5

Sample Output 2🔗

2 1 1 3 2 1 3 2 1 3 3 2 1 3 2 2 1 2 1 1 1

Sample Input 3🔗

5
5
0 2 5 9 14
2
2 1
2 2

Sample Output 3🔗

impossible

Following tremendous advances in space flight control software and equally impressive innovations in reality TV crowdfunding, humans have successfully settled a number of planets, moons, asteroids, and various other kinds of funny-shaped rocks across our solar system.

To celebrate, the Galactic President has elected to create a new holiday called "Solar Night". At the crux of the event, she decrees, every settlement will simultaneously launch colourful fireworks into the darkness of night.

Night, like most things, is a difficult problem in space. Every spacebound object has its own day length and period of rotation. Thankfully all of the settlements did, at least, start their clocks at the same moment. Settlements may have started in daylight or darkness and so it is possible that the first recorded sunrise can be either before or after the first hour of sunset.

By convention, the President’s term lasts for exactly $1825$ days as measured by the planet with the longest period of rotation. The celebration needs to happen within that time or it will not serve its intended purpose.

Determine how many hours must pass for us to find a suitable time to celebrate Solar Night.

Input🔗

• One line containing the integer $N$ ($1 \le N \le 20$), the number of settlements.
• $N$ lines, each containing three integers:
  • $H$ ($2 \le H \le 100$), the number of hours in this settlement’s solar day.
  • $R$ and $T$ ($0 \le R, T \le H - 1, R \neq T$), the hours of sunrise and sunset respectively.

At sunrise and sunset, a settlement is in darkness. At times strictly in between sunrise and sunset, a settlment is in daylight.

Output🔗

Output the number of hours that must pass from when the settlement clocks began until each settlement is in darkness. If no suitable time occurs in the first $1825$ days, output impossible.

Sample Input 1🔗

2
24 7 19
24 18 6

Sample Output 1🔗

6

Sample Input 2🔗

3
10 8 2
15 5 10
20 15 10

Sample Output 2🔗

12

Sample Input 3🔗

2
6 4 2
12 7 5

Sample Output 3🔗

impossible

Sample Input 4🔗

2
10 5 6
10 6 5

Sample Output 4🔗

5

For the grand opening of the algorithmic games in NlogNsglow, a row of tower blocks is set to be demolished in a grand demonstration of renewal. Originally the plan was to accomplish this with controlled explosions, one for each tower block, but time constraints now require a hastier solution.

To help you remove the blocks more rapidly you have been given the use of a Universal Kinetic / Incandescent Energy Particle Cannon (UKIEPC). On a single charge, this cutting-edge contraption can remove either all of the floors in a single tower block, or all the $x$-th floors in all the blocks simultaneously, for user’s choice of the floor number $x$. In the latter case, the blocks that are less than $x$ floors high are left untouched, while for blocks having more than $x$ floors, all the floors above the removed $x$-th one fall down by one level.

Given the number of floors of all towers, output the minimum number of charges needed to eliminate all floors of all blocks.

Input🔗

The first line of input contains the number of blocks $n$, where $2 \le n \le 100 000$. The second line contains $n$ consecutive block heights $h_i$ for $i = 1, 2, ..., n$, where $1 \le h_i \le 1 000 000$.

Output🔗

Output one line containing one integer: the minimum number of charges needed to tear down all the blocks.

Sample Input 1🔗

6
2 1 8 8 2 3

Sample Output 1🔗

5

Sample Input 2🔗

5
1 1 1 1 10

Sample Output 2🔗

2