+ محدودیت زمان: ۰.۵ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
در ایام شیوع کرونا مدارس زیادی تصمیم گرفتند بعد از اتمام ایام قرنطینه برای جبران جاماندگی ناشی از آموزش مجازی، آموزش حضوری خود را به صورت شبانه روزی و بدون هیچ گونه تعطیلاتی دایر کنند! مدیران مدارس تصمیم گرفتند که تمامی روزهای تعطیل از جمله جمعهها اساتید سر کلاس حضور پیدا کنند.
هر معلمی موظف است که با یک دوره تناوب ثابت در مدرسه حضور پیدا کند. به طور مثال آقای کوشکی دبیر درس ریاضی موظف است هر دو روز یک بار و آقای زمانی دبیر ادبیات موظف است هر سه روز یک بار به مدرسه بیاید. اولین روز سال تحصیلی (اول مهر) تمامی معلمها به مدرسه میآیند و کار خود را از آن روز شروع میکنند. دانشآموزان میخواهند بفهمند اولین روزی که دوباره همه معلمها با هم جمع میشوند؛ روز چندم ماه است؟ (همهی ماهها سی روزه هستند.)
# ورودی
1. در اولین خط ورودی $n$ (تعداد معلمها) وارد میشود.
2. در هر خط از $n$ خط بعدی، دوره تناوب حضور معلمها وارد میشود.
$$1 \le n \le 5$$
$$1 \le a_i \le 30$$
# خروجی
در تنها خط خروجی، اولین روز حضور دوبارهی همه معلمها نمایش داده میشود.
# مثال
## ورودی نمونه ۱
```
2
6
7
```
## خروجی نمونه ۱
```
13
```
<details>
<summary>توضیحات نمونهی ۱</summary>
این مدرسه تنها دو معلم دارد که معلم اول هر ۶ روز یک بار و معلم دوم هر ۷ روز یک بار به مدرسه میآیند. این دو معلم پس از اولین روز مدارس، ۴۲ روز بعد در ۴۳امین روز سال تحصیلی دوباره با هم به مدرسه میآیند و آن روز ۱۳ام ماه است. بنابراین در خروجی عدد ۱۳ چاپ میشود.
</details>
## ورودی نمونه ۲
```
4
2
4
13
12
```
## خروجی نمونه ۲
```
7
```
<details>
<summary>توضیحات نمونهی ۲</summary>
این مدرسه چهار معلم دارد که هر معلم به ترتیب هر ۲ روز یک بار، هر ۴ روز یک بار، هر ۱۳ روز یکبار و هر ۱۲ روز یک بار به مدرسه میآیند. این معلمها پس از اولین روز مدارس، ۱۵۶ روز بعد در ۱۵۷امین روز تحصیلی دوباره با هم به مدرسه میآیند و آن روز ۷ام ماه است. بنابراین در خروجی عدد ۷ چاپ میشود.
</details>
مدرسه شبانه روزی
+ محدودیت زمان: ۰.۵ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
در این سوال شما میبایست بازی **اتللو** را پیادهسازی کنید.
این بازی به صورت دو نفره انجام میشود. ابتدا چهار مهره مطابق شکل در وسط صفحه قرار میگیرند. مهرهی تیره بازی را آغاز میکند. هر یک از دو بازیکن به نوبت یک مهره (از طرف رنگ خود) را در صفحه قرار میدهند به طوری که حداقل یکی از مهرههای حریف را در حداقل یکی از راستاهای هشتگانه محاصره کند. سپس تمامی مهرههای محاصرهشده در هر یک از راستاهای هشتگانه تغییر رنگ میدهند.
زمانی که هیچ یک از بازیکنان حرکتی نداشته باشند؛ بازی به پایان میرسد و بازیکنی که تعداد مهرههای بیشتری روی صفحه داشته باشد؛ برنده است.

**نکته ۱:** تنها مهرههایی را میتوان تصاحب کرد که بین مهرهی جدید و مهرههای قبلی محاصره شده باشند یعنی مهرههایی که در جریان بازی در بین مهرههای ناهمرنگ قرار میگیرند؛ تغییر رنگ نمیدهند.
**نکته ۲:** در صورتی یکی از بازیکنان در نوبت خود، مکانی برای محاصره حریف نداشته باشد و نتواند حتی یک مهره او را محاصره کند؛ نوبت خود را از دست میدهد و حرکت به حریف واگذار میشود تا زمانی که امکان محاصره برایش ایجاد شود.
# ورودی
1. در اولین خط ورودی $n$ (مجموع تعداد حرکتهای بازیکن اول و دوم) وارد میشود.
2. در خط دوم، حرکت بازیکنان با یک فاصله از هم وارد میشود.
هر حرکت شامل رشتهی دو کاراکتری است که کاراکتر اول یکی از حروف $A$ تا $H$ و کاراکتر دوم عددی بین ۱ تا ۸ خواهد بود. (تضمین میشود که تمامی حرکتها در ورودی مجاز هستند.)
$$1 \le n \le 60$$
# خروجی
در تنها خط خروجی به ترتیب امتیاز فعلی بازیکن اول و دوم با یک فاصله از هم نمایش داده میشود.
# مثال
## ورودی نمونه ۱
```
3
D3 E3 F5
```
## خروجی نمونه ۱
```
6 1
```
<details>
<summary>توضیحات نمونهی ۱</summary>
+ حرکت اول: بازیکن اول مهره تیره را در خانهی $D3$ قرار میدهد و مهرهی خانهی $D4$ را محاصره میکند و مهرهی محاصره شده تیره میشود.
+ حرکت دوم: بازیکن دوم مهره روشن را در خانهی $E3$ قرار میدهد و مهرهی خانهی $E4$ را محاصره میکند و مهرهی محاصره شده روشن میشود.
+ حرکت سوم: بازیکن اول مهره تیره را در خانهی $F5$ قرار میدهد و مهرههای خانهی $E4$ و $E5$ را محاصره میکند و مهرههای محاصره شده تیره میشوند.
در تنها خط خروجی ابتدا امتیاز بازیکن اول (۶ مهرهی تیره) و سپس امتیاز بازیکن دوم (۱ مهرهی روشن) وارد میشود.
</details>
## ورودی نمونه ۲
```
4
F5 F4 C3 C4
```
## خروجی نمونه ۲
```
4 4
```
<details>
<summary>توضیحات نمونهی ۲</summary>
+ حرکت اول: بازیکن اول مهره تیره را در خانهی $F5$ قرار میدهد و مهرهی خانهی $E5$ را محاصره میکند و مهرهی محاصره شده تیره میشود.
+ حرکت دوم: بازیکن دوم مهره روشن را در خانهی $F4$ قرار میدهد و مهرهی خانهی $E4$ را محاصره میکند و مهرهی محاصره شده روشن میشود.
+ حرکت سوم: بازیکن اول مهره تیره را در خانهی $C3$ قرار میدهد و مهرههای خانهی $D4$ را محاصره میکند و مهرهی محاصره شده تیره میشود.
+ حرکت چهارم: بازیکن دوم مهره تیره را در خانهی $C4$ قرار میدهد و مهرههای خانهی $D4$ را محاصره میکند و مهرهی محاصره شده روشن میشود.
در تنها خط خروجی ابتدا امتیاز بازیکن اول (۴ مهرهی تیره) و سپس امتیاز بازیکن دوم (۴ مهرهی روشن) وارد میشود.
</details>
اتللو
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
یک زمین موزاییک کاری شدهی پهناور داریم و بچههای محل میخواهند در آن بازی کنند. مشکلی که وجود دارد این است که بعضی از این موزاییکها شکسته شده و بچهها میترسند که پایشان گیر کند و آسیب ببینند. آنها تصمیم گرفتند که یک زیر مستطیل به تعداد موزاییکهای مشخص از این زمین را انتخاب کنند که در آن هیچ موزاییک خرابی وجود نداشته باشد. حال شما باید به آنها بگویید برای این کار چند انتخاب دارند؟
# ورودی
1. در خط اول ورودی، به ترتیب $X$ (اندازهی طول زمین) و $Y$ (اندازهی عرض زمین) با یک فاصله از هم وارد میشود.
2. در خط دوم ورودی، $S$ (تعداد موزاییکهای زمین انتخابی) وارد میشود.
3. در خط سوم ورودی، $n$ (تعداد موزاییک های خراب) وارد میشود.
4. سپس در $n$ خط بعدی در هر خط دو عدد طول و عرض مختصات موزاییکهای شکسته شده با یک فاصله از هم وارد میشوند. (مختصات تکراری وارد نمیشود.)
$$ 1 \le X, Y \le 250$$
$$ 0 \le n \le X * Y $$$$ 1 \le S \le X * Y $$$$ 1 \le x_i \le X $$$$ 1 \le y_i \le Y $$
# خروجی
خروجی تنها شامل یک عدد است که تعداد زیر مستطیلهای با تعداد $S$ موزاییک را نمایش میدهد.
# مثال
## ورودی نمونه ۱
```
8 2
4
1
3 1
```
## خروجی نمونه ۱
```
12
```
<details>
<summary>توضیحات نمونهی ۱</summary>
با توجه به تصویر و جدول زیر تعداد زمینهای بازی مستطیل شکل با ۴ موزاییک، ۱۲ تاست. بنابراین عدد ۱۲ در خروجی چاپ میشود.

| |موزاییکهای تحت پوشش|
|:-----:|:-----------------:|
|زمین ۱|۱ ۲ ۸ ۹ |
|زمین ۲|۳ ۴ ۱۱ ۱۲|
|زمین ۳|۴ ۵ ۱۲ ۱۳|
|زمین ۴|۵ ۶ ۱۳ ۱۴|
|زمین ۵|۶ ۷ ۱۴ ۱۵|
|زمین ۶|۳ ۴ ۵ ۶ |
|زمین ۷|۴ ۵ ۶ ۷ |
|زمین ۸|۸ ۹ ۱۰ ۱۱|
|زمین ۹|۹ ۱۰ ۱۱ ۱۲|
|زمین ۱۰|۱۰ ۱۱ ۱۲ ۱۳|
|زمین ۱۱|۱۱ ۱۲ ۱۳ ۱۴|
|زمین ۱۲|۱۲ ۱۳ ۱۴ ۱۵|
</details>
## ورودی نمونه ۲
```
8 3
2
8
1 1
2 2
3 3
4 2
5 1
6 2
7 3
8 2
```
## خروجی نمونه ۲
```
11
```
<details>
<summary>توضیحات نمونهی ۲</summary>
با توجه به تصویر و جدول زیر تعداد زمینهای بازی مستطیل شکل با ۲ موزاییک، ۱۱ تاست. بنابراین عدد ۱۱ در خروجی چاپ میشود.

| |موزاییکهای تحت پوشش|
|:-----:|:-----------------:|
|زمین ۱|۱ ۲|
|زمین ۲|۲ ۳|
|زمین ۳|۲ ۸|
|زمین ۴|۷ ۱۱|
|زمین ۵|۱۱ ۱۲|
|زمین ۶|۹ ۱۴|
|زمین ۷|۱۳ ۱۴|
|زمین ۸|۱۴ ۱۵|
|زمین ۹|۴ ۵|
|زمین ۱۰|۵ ۶|
|زمین ۱۱|۵ ۱۰|
</details>
زمین بازی ۱
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
مسئلهی قبل را در نظر بگیرید. یک زمین بازی را خوب مینامیم که علاوه بر اینکه مستطیل شکل باشد و در آن هیچ موزاییک خرابی وجود نداشته باشد؛ از هیچ یک از اضلاعش قابل گسترش نباشد. این بار از شما میخواهیم تعداد زمینهای خوب را بیابید.
# ورودی
1. در خط اول ورودی، به ترتیب $X$ (اندازهی طول زمین) و $Y$ (اندازهی عرض زمین) با یک فاصله از هم وارد میشود.
2. در خط سوم ورودی، $n$ (تعداد موزاییک های خراب) وارد میشود.
3. سپس در $n$ خط بعدی در هر خط دو عدد طول و عرض مختصات موزاییکهای شکسته شده با یک فاصله از هم وارد میشوند.
توجه: برخلاف سوال قبل، در ورودی این سوال $S$ (تعداد موزاییکهای زمین انتخابی) نداریم.
$$ 1 \le X, Y \le 250 $$
$$ 0 \le n \le X * Y $$
$$ 1 \le x_i \le X $$$$ 1 \le y_i \le Y $$
# خروجی
خروجی تنها شامل یک عدد است که تعداد زمینهای خوب را نمایش میدهد.
# مثال
## ورودی نمونه ۱
```
8 2
1
3 1
```
## خروجی نمونه ۱
```
3
```
<details>
<summary>توضیحات نمونهی ۱</summary>
با توجه به تصویر و جدول زیر تعداد زمینهای خوب ۳ تاست. بنابراین عدد ۳ در خروجی چاپ میشود.

| |موزاییکهای تحت پوشش|
|:--------:|:-----------------:|
|زمین خوب ۱|۱ ۲ ۸ ۹|
|زمین خوب ۲|۳ ۴ ۵ ۶ ۷ ۱۱ ۱۲ ۱۳ ۱۴ ۱۵|
|زمین خوب ۳|۸ ۹ ۱۰ ۱۱ ۱۲ ۱۳ ۱۴ ۱۵|
</details>
## ورودی نمونه ۲
```
8 3
8
1 1
2 2
3 3
4 2
5 1
6 2
7 3
8 2
```
## خروجی نمونه ۲
```
9
```
<details>
<summary>توضیحات نمونهی ۲</summary>
با توجه به تصویر و جدول زیر تعداد زمینهای خوب ۹ تاست. بنابراین عدد ۹ در خروجی چاپ میشود.

| |موزاییکهای تحت پوشش|
|:--------:|:-----------------:|
|زمین خوب ۱|۱ ۲ ۳|
|زمین خوب ۲|۲ ۸|
|زمین خوب ۳|۷ ۱۱|
|زمین خوب ۴|۱۱ ۱۲|
|زمین خوب ۵|۱۳ ۱۴ ۱۵|
|زمین خوب ۶|۹ ۱۴|
|زمین خوب ۷|۴ ۵ ۶|
|زمین خوب ۸|۵ ۱۰|
|زمین خوب ۹|۱۶|
</details>
زمین بازی ۲
+ محدودیت زمان:۲ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
یکی از بهروزترین و پیشرفتهترین روشهای تحلیل داده و خلق ارزش با استفاده از دادهها، تحلیل داده مبتنی بر گراف است. در این روش همهی دادههای موجود در مسئله به صورت راسها و یالهای یک گراف بزرگ مدل میشوند و جواب سوالات تحلیلگر داده با اجرای الگوریتمهای پرکاربرد گراف آماده میشود.
یکی از این الگوریتمها یافتن تمام مسیرهای موجود بین دو راس مشخص از گراف است که کاربرد وسیعی در تحلیل دادههای مالی دارد. مثالهای عملیاتی زیر را در نظر بگیرید:
**مثال اول**: یک مزایده برگزار شده است که نتیجه آن واگذاری یک ملک/کارخانه به قیمت پایینتر از ارزش واقعی بوده، میخواهیم در مورد احتمال رد و بدل شدن رشوه بین برنده مزایده و برگزار کنندگان تحقیق کنیم.
اگر رشوهدهنده با چند واسطه رشوه داده باشد تشخیص آن با روشهای معمولی سخت است اما با الگوریتم یافتن مسیرها میتوان تمام مسیرهای انتقال پول بین رشوهدهنده و رشوهگیرنده به طول ۳، ۴ یا حتی بیشتر را روی گراف روابط مالی در چند ثانیه به دست آورد. در صورت وجود حداقل یک مسیر احتمال وجود تبانی در این مزایده بالاست.
**مثال دوم**: یکی از حوزههای پرکاربرد تحلیل دادهی گرافی، حوزهی بانکی است. یکی از مسائل آن احتمال تبانی وام گیرنده با کارمندان شعبهی بانک است به این صورت که وام گیرنده ممکن است با پرداخت رشوه به کارمند بانک بتواند وام کلانی را بگیرد در صورتی که شرایط دریافت آن وام را نداشته (مثلاً از بدهکاران بانکی بوده و قسطهای وامهای کلان قبلی را هنوز تسویه نکرده است)
واحد بازرسی بانک با اجرای الگوریتم یافتن مسیرها روی تراکنشها و خرید و فروشهای وام گیرنده و کارمندان بانکی که از آن وام گرفته است به راحتی میتواند به وجود رابطهی مالی (حتی با چندین واسطه) پی ببرد و جلوی ادامهی تخلفات را بگیرد.
----------
در این مسئله یک گراف (جهتدار یا بدون جهت) به همراه یک راس مبدا و یک راس مقصد به شما داده میشود و از شما خواسته میشود تمام مسیرهای از مبدا تا مقصد که طولشان در بازهی مشخصی قرار دارد، را بیابید. سپس تعداد و شناسهی تمام یالهای موجود در این مسیرها را در خروجی چاپ کنید.
**توجه**: برنامهی شما حتما باید به زبان **$Java$** باشد و شما مجاز به ایجاد هر گونه کلاس، تابع، اینترفیس و ... هستید.
### نکات مهم:
1. جهتدار یا بدون جهت بودن گراف در ورودی مشخص میشود (در صورتی که گراف جهتدار باشد، جهت یالها باید همجهت با مسیر باشد و در صورت بدون جهت بودن گراف جهت یالها هیچ اهمیتی ندارد).
2. کمترین و بیشترین طول مسیر مجاز در ورودی ذکر میشود.
3. هر یال گراف شامل سه عدد برای شناسهی یال، شمارهی راس اول و شمارهی راس دوم است. (شناسه یالها از هم متمایز هستند.)
4. در یک مسیر مجاز، از یک یال یا راس دو بار عبور نمیکنیم. (در یک مسیر مجاز دور نداریم.)
# ورودی
1. در خط اول ورودی $n$ (تعداد راسهای گراف) و $m$ (تعداد یالهای گراف) با یک فاصله از هم وارد میشود. (تمامی راسهای گراف از ۱ تا $n$ شماره گذاری میشوند.)
2. در خط دوم $s$ (شمارهی راس مبدا) و $t$ (شمارهی راس مقصد) وارد میشوند.
3. در خط سوم $min$ (کمترین طول مسیر) و $max$ (بیشترین طول مسیر) وارد میشود.
4. در خط چهارم ورودی $d$ (جهتدار بودن یا بدون جهت بودن گراف) وارد میشود. در صورتی که ۱ باشد، گراف جهتدار است و در صورتی که ۰ باشد، گراف بدون جهت است.
5. سپس در $m$ خط بعدی در هر خط اطلاعات یکی از یالهای گراف وارد میشود. اطلاعات هر یال شامل سه عدد برای شناسهی یال، شمارهی راس اول و دوم (برای گرافهای جهتدار راس اول مبدا و راس دوم مقصد) خواهد بود.
$$1 \le n \le 1\ 000 $$ $$1 \le m \le 5 * n$$
$$1 \le s, t \le n$$
$$ 1 \le min, max \le 8 $$
$$ min \le max $$
# خروجی
در خط اول خروجی تعداد تمام یالهایی که در مسیرهایی به کمترین و بیشترین طول داده شده وجود دارند نمایش داده میشوند.
در خط دوم خروجی شناسهی تمام یالهای مذکور به ترتیب (از کوچک به بزرگ) با یک فاصله از هم نمایش داده میشوند.
# مثال
## ورودی نمونه ۱
```
3 4
1 2
2 4
0
1 1 2
2 2 3
3 1 3
4 3 1
```
## خروجی نمونه ۱
```
3
2 3 4
```
<details>
<summary>توضیحات نمونهی ۱</summary>
با توجه به جدول زیر تعداد مسیر به حداقل طول ۲ و حداکثر طول ۴، ۲ تاست و یالهای ۲، ۳ و ۴ در آن وجود دارند. بنابراین عدد ۳ (تعداد یالها) و شناسهی یالها در خروجی چاپ میشود.

| |یالهای موجود|
|:----:|:----------:|
|مسیر ۱|۳ ۲|
|مسیر ۲|۴ ۲|
</details>
## ورودی نمونه ۲
```
5 6
1 3
2 5
1
1 2 1
2 2 3
3 1 3
4 1 4
5 5 4
6 5 3
```
## خروجی نمونه ۲
```
0
```
<details>
<summary>توضیحات نمونهی ۲</summary>
با توجه به جهتدار بودن گراف هیچ مسیری از مبدا (راس ۱) به مقصد (راس ۳) به حداقل طول ۲ و حداکثر طول ۵، وجود ندارد. بنابراین عدد ۰ در خروجی چاپ میشود.

</details>
کشف تبانی!
+ محدودیت زمان: ۴ ثانیه
+ محدودیت حافظه: ۱۰۲۴ مگابایت
----------
مالیات اصلیترین راه تامین درآمد بسیاری از کشورها از جمله کشورهای پیشرفته است و هزینهی بسیاری از پروژههای زیرساختی، عمرانی و حتی حقوق کارمندان دولت، معلمان و ... از طریق دریافت مالیات از کسبه، شرکتها و ... تامین میشود. فرار مالیاتی به زبان ساده یعنی مالیاتدهنده تلاش کند کمتر از میزان واقعی مالیات پرداخت کند. مثلاً فرض کنید یک کاسب در طول سال، ۱۰۰ میلیون تومان سود (مجموع درآمد منهای هزینهها) داشته و با نرخ ۱۵ درصد باید ۱۵ میلیون تومان مالیات بپردازد. حالا اگر این کاسب تلاش کند با روشهای مختلف میزان سود اصلی خود را کمتر نشان دهد، مالیات کمتری نیز میپردازد. به این عمل فرار مالیاتی میگوییم.
در حال حاضر فرار مالیاتی یک چالش بزرگ در کشورهای دنیاست، گزارشهای مختلف نشان میدهد در ایران خودمان سالانه بین ۴۰ تا ۱۵۰ هزار میلیارد تومان فرار مالیاتی داریم. یکی از موثرترین راههای جلوگیری از فرار مالیاتی در برخی از کشورهای پیشرفته تحلیل دادههای مالی به صورت گراف است. به این صورت که تمام دادههای مالی شامل تراکنشها، خرید و فروشها و مالکیتها را به صورت راسهای گراف اصلی (گرافی بسیار بزرگ) مدل میکنیم و انواع شکلهایی که احتمال دارد فرار مالیاتی باشد را به صورت گراف الگو (گرافی بسیار کوچک) مدل میکنیم. سپس در گراف اصلی زیرگرافهایی که شبیه گراف الگوی فرار مالیاتی باشد را پیدا میکنیم.
مثالهای از تخلفات که به راحتی قابل تبدیل به گرافهای الگو هستند:
+ کاسبی که در سال گذشته یک آپارتمان با قیمت بالای سه میلیارد تومان و یک خودروی ۵۰۰ میلیون تومانی خریده است اما در اظهارنامه مالیاتی سودش را کمتر از ۵۰ میلیون اعلام کرده است.
+ شرکتی که در اظهارنامه مالیاتی ضررده اعلام شده اما پاداش آخر سال مدیران آن صدها میلیون تومان بوده است.
در ادامه حالت ساده شدهی این مسئله آورده شده، که حل آن میتواند مقدمهای بر حل مسئلهی فرار مالیاتی باشد، پس تلاش خود را به کار ببرید، این گوی و این میدان!
----------
در این مسئله یک گراف اصلی و یک گراف الگو به شما داده میشود. حال شما میبایست تعداد زیر گرافهای موجود در گراف اصلی را پیدا کنید به طوری که این زیرگرافها مشابه گراف الگو باشند. (برای فهم بهتر مسئله به شکلهای پایین صفحه مراجعه کنید)
**توجه**: برنامهی شما حتما باید به زبان **$Java$** باشد و شما مجاز به ایجاد هر گونه کلاس، تابع، اینترفیس و ... هستید.
### نکات مهم:
1. گرافها رنگی و جهتدار هستند.
2. گراف الگو ضعیفا همبند است. (در صورتی که جهت یالها را در نظر نگیریم، گراف ما همبند است)
3. بین هر دو راس گراف الگو حداکثر یک یال در هر جهت وجود دارد.
4. هر راس گراف شامل یک شناسه یکتا و یک رنگ است.
5. هر یال گراف شامل یک شناسه راس مبدا و یک شناسه راس مقصد است.
# ورودی
### اطلاعات گراف اصلی
1. در خط اول ورودی $n_1$ (تعداد راسهای گراف اصلی) وارد میشود.
2. سپس در $n_1$ خط بعدی یک رشته (شناسه راس) و $a_i$ (شماره رنگ راس) برای راسهای گراف اصلی با یک فاصله از هم وارد میشوند.
3. سپس مقدار $m_1$ (تعداد یالهای گراف اصلی) وارد میشود.
4. سپس در $m_1$ خط بعدی دو رشته برای شناسهی راس مبدا و شناسهی راس مقصد یالهای گراف اصلی با یک فاصله از هم وارد میشوند.
### اطلاعات گراف الگو
5. در خط بعد $n_2$ (تعداد راسهای گراف الگو) وارد میشود.
6. سپس در $n_2$ خط بعدی یک رشته (شناسه راس) و $b_i$ (شماره رنگ راس) برای راسهای گراف الگو با یک فاصله از هم وارد میشوند.
7. سپس مقدار $m_2$ (تعداد یالهای گراف الگو) وارد میشود.
8. سپس در $m_2$ خط بعدی دو رشتهی شناسهی راس مبدا و شناسهی راس مقصد یالهای گراف الگو با یک فاصله از هم وارد میشوند.
$$1 \le n_1 \le 30\ 000$$
$$1 \le a_i \le 4$$
$$1 \le m_1 \le 10*n_1$$
$$1 \le n_2 \le 5$$
$$1 \le b_i \le 4$$
$$1 \le m_2 \le 20$$
# خروجی
خروجی تنها شامل یک عدد است که تعداد زیرگرافهای موجود از گراف اصلی (شبیه به گراف الگو) را نشان میدهد.
# مثال
## ورودی نمونه ۱
```
5
1 1
2 2
3 2
4 2
5 2
8
1 2
1 5
2 3
2 4
2 5
3 4
5 3
5 4
3
A 1
B 2
C 2
2
A B
B C
```
## خروجی نمونه ۱
```
5
```
<details>
<summary>توضیحات نمونهی ۱</summary>
گراف اصلی نمونه ۱:
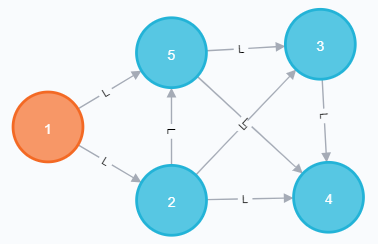
گراف الگو نمونه ۱:
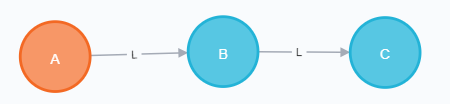
با توجه به جدول زیر تعداد زیرگرافهای مشابه گراف الگو در گراف اصلی، ۵ تاست، بنابراین عدد ۵ در خروجی چاپ میشود.
| |راس A|راس B|راس C|
|:-------:|:---:|:---:|:---:|
|زیرگراف ۱|راس ۱|راس ۲|راس ۳|
|زیرگراف ۲|راس ۱|راس ۲|راس ۴|
|زیرگراف ۳|راس ۱|راس ۲|راس ۵|
|زیرگراف ۴|راس ۱|راس ۵|راس ۳|
|زیرگراف ۵|راس ۱|راس ۵|راس ۴|
</details>
## ورودی نمونه ۲
```
5
1 1
2 2
3 2
4 2
5 2
4
1 2
1 3
1 4
1 5
3
A 1
B 2
C 2
2
A B
A C
```
## خروجی نمونه ۲
```
12
```
<details>
<summary>توضیحات نمونهی ۲</summary>
گراف اصلی نمونه ۲:
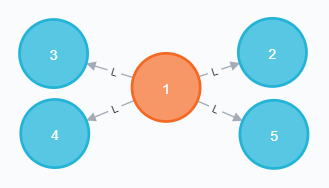
گراف الگو نمونه ۲:
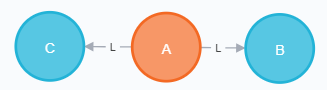
با توجه به جدول زیر تعداد زیرگرافهای مشابه گراف الگو در گراف اصلی، ۱۲ تاست، بنابراین عدد ۱۲ در خروجی چاپ میشود.
| |راس A|راس B|راس C|
|:--------:|:---:|:---:|:---:|
|زیرگراف ۱ |راس ۱|راس ۲|راس ۳|
|زیرگراف ۲ |راس ۱|راس ۲|راس ۴|
|زیرگراف ۳ |راس ۱|راس ۲|راس ۵|
|زیرگراف ۴ |راس ۱|راس ۳|راس ۲|
|زیرگراف ۵ |راس ۱|راس ۳|راس ۴|
|زیرگراف ۶ |راس ۱|راس ۳|راس ۵|
|زیرگراف ۷ |راس ۱|راس ۴|راس ۲|
|زیرگراف ۸ |راس ۱|راس ۴|راس ۳|
|زیرگراف ۹ |راس ۱|راس ۴|راس ۵|
|زیرگراف ۱۰|راس ۱|راس ۵|راس ۲|
|زیرگراف ۱۱|راس ۱|راس ۵|راس ۳|
|زیرگراف ۱۲|راس ۱|راس ۵|راس ۴|
</details>
## ورودی نمونه ۳
```
2
1 1
2 1
2
1 2
2 1
2
A 1
B 1
1
A B
```
## خروجی نمونه ۳
```
2
```
<details>
<summary>توضیحات نمونهی ۳</summary>
گراف اصلی نمونه ۳:

گراف الگو نمونه ۳:

با توجه به جدول زیر تعداد زیرگرافهای مشابه گراف الگو در گراف اصلی، ۲ تاست، بنابراین عدد ۲ در خروجی چاپ میشود.
| |راس A|راس B|
|:-------:|:---:|:---:|
|زیرگراف ۱|راس ۱|راس ۲|
|زیرگراف ۲|راس ۲|راس ۱|
</details>