+ محدودیت زمان: ۰.۵ ثانیه
+ محدودیت حافظه: ۶۴ مگابایت
----------
ابواسحاق که از دوستداران همیشگی کدکاپ است، بعد از شکست در کدکاپ ۴ حسابی کلافه شد و تصمیم گرفت دنبال یک تیم حسابی برای بازگشت پرقدرت خود و دوستانش به کدکاپ ۵ بگردد. او که میخواست حداکثر نفوذ در کدکاپ را داشته باشد، تصمیم گرفت خودش تمام تیمبندیها را انجام دهد.
دوستان ابواسحاق از سه شهر مختلفاند و بعضی از آنها لپتاپ دارند. به طور دقیقتر، از شهر $i$ اُم $a_i$ نفر دارای لپتاپ و $b_i$ نفر بدون لپتاپ، میخواهند در مسابقه شرکت کنند و ابواسحاق میخواهد طوری آنها را تیمبندی کند که شرایط زیر برای هر تیم برقرار باشد:
+ هر یک از تیمها دو نفره باشد.
+ هر تیم شامل دقیقاً یک نفر دارای لپتاپ و دقیقاً یک نفر بدون لپتاپ باشد.
+ اعضای هر تیم از یک شهر باشند.
ابواسحاق در حال آماده شدن برای کدکاپ ۵ است و سرش شلوغ است. برای همین از شما میخواهد بیشینه تعداد تیمهایی را که با توجه به شرایط بالا میتواند تشکیل دهد را به او بگویید.
# ورودی
ورودی دارای ۶ خط و در هر خط یک عدد است که به ترتیب نشانگر مقادیر $a_1$، $b_1$، $a_2$، $b_2$، $a_3$ و $b_3$ هستند.
$$ 1 \le a_i, b_i \le 100 $$
# خروجی
در خروجی باید بیشینه تعداد تیمهایی که میتوان تشکیل داد را خروجی دهید.
## ورودی نمونه ۱
```
3
2
1
5
6
7
```
## خروجی نمونه ۱
```
9
```
از شهر یک و دو و سه، به ترتیب حداکثر ۲ و ۱ و ۶ تیم میتوان تشکیل داد.
## ورودی نمونه ۲
```
1
1
2
2
3
3
```
## خروجی نمونه ۲
```
6
```
از شهر یک، دو و سه، به ترتیب حداکثر ۱ و ۲ و ۳ تیم میتوان تشکیل داد.
تیم کشی
+ محدودیت زمان: ۰.۵ ثانیه
+ محدودیت حافظه: ۶۴ مگابایت
----------
ابواسحاق که برای کدکاپ ۵ لحظه شماری میکرد، هر روزی که از برگزاری کدکاپ ۴ میگذشت روی تختهٔ خود یک چوب خط میکشید؛ اما چند روز پیش متوجه شد که کل تختهاش پر شده و باید آن را پاک کند. از آنجایی که تا کدکاپ چیزی باقی نمانده، از شما کمک میخواهد که تختهاش را برایش پاک کنید.
تختهٔ ابواسحاق به شکل یک جدول $n \times m$ کاملاً سیاه است و یک تخته پاک کن $a \times b$ در اختیار داریم. در هر مرحله میتوانیم تخته پاک کن را **یا به صورت افقی و یا به صورت عمودی** (به طوری که اضلاع تخته پاک کن موازی با طول و عرض تخته باشد) ، بر روی تخته قرار دهیم و آن را به سمت دیگری بِکِشیم تا تمام خانههایی که تخته پاک کن از روی آن عبور میکند، سفید شوند.
شما باید کمینه تعداد مراحل لازم را بگویید که بتوان تخته را کاملاً سفید کرد.
**توجه کنید که در ابتدا تخته پاک کن بر روی تخته قرار ندارد.**
# ورودی
ورودی شامل ۴ خط و در هر خط یک عدد است که به ترتیب نشانگر مقادیر $n$، $m$، $a$ و $b$ هستند.
$$1 \le n, m \le 10^{9}$$
$$1 \le a, b \le \min (n,m)$$
# خروجی
در خروجی باید کمینه تعداد مراحل لازم را چاپ کنید.
## ورودی نمونه ۱
```
3
3
1
3
```
## خروجی نمونه ۱
```
1
```
برای این تست، میتوانیم تخته پاککن را به صورت افقی در بالای تخته قرار داده و آن را تا پایین تخته بِکِشیم. در این صورت کل تخته در ۱ مرحله پاک میشود. (مطابق شکل زیر)
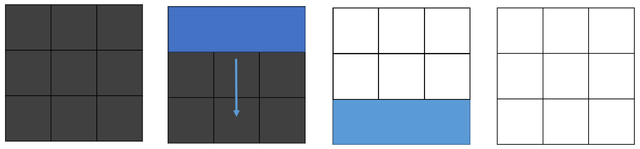
خانههای آبی نشان دهندهٔ تخته پاک کن هستند که در جدول قرار گرفتهاند.
## ورودی نمونه ۲
```
2
2
1
1
```
## خروجی نمونه ۲
```
2
```
مطابق شکل زیر در دو مرحله میتوان تخته را پاک کرد:
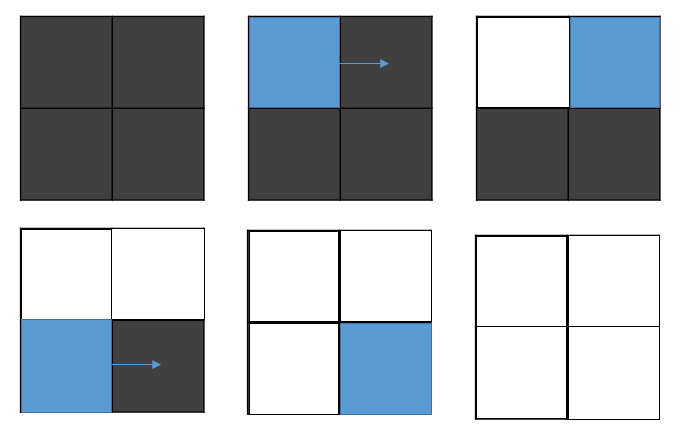
چوب خطهای نامتناهی
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
بعد از بیش از دو سال انتظار و جستجو برای هم تیمی، ابواسحاق متوجه شد کدکاپ ۵ انفرادی برگزار میشود! برای همین کلی ناراحت شد و رشته افکارش تبدیل به گراف شد! اکنون برای باز گرداندن آن به حالت عادی، دست به دامن شما شده است.
رشته افکار ابواسحاق یک گرافِ سادهٔ همبند $n$ راسی و $m$ یالی است. او تصمیم دارد برای بازگرداندن رشته افکارش در طی $k$ مرحله، هر مرحله یک یال به آن اضافه کند به طوری که گراف حاصل، ساده باقی بماند و دارای حداقل یک دور به طول فرد باشد. (گراف ساده گرافی است که دارای [یال چندگانه](https://fa.wikipedia.org/wiki/%DA%AF%D8%B1%D8%A7%D9%81_%DA%86%D9%86%D8%AF%DA%AF%D8%A7%D9%86%D9%87) و [طوقه](https://fa.wikipedia.org/wiki/%D8%AD%D9%84%D9%82%D9%87_%28%D9%86%D8%B8%D8%B1%DB%8C%D9%87_%DA%AF%D8%B1%D8%A7%D9%81%29) نباشد)
امّا او که سلامت روانش بسیار برایش مهم است، قبل از این که دست به کار شود از شما میخواهد تا تعداد روشهای مختلف انجام این عمل را به او بگویید. از آنجا که تعداد حالات، ممکن است بسیار زیاد باشد، باقی ماندهٔ تقسیم آن بر $10^{9} + 7$ را به او بگویید (دو روش از انجام $k$ مرحله را متمایز گوییم، اگر مرحلهای مثل $i$ وجود داشته باشد که دو سر یال اضافه شده در روش اول برابر با دو سر یال اضافه شده در روش دوم نباشد).
**دقت کنید که ترتیب اضافه کردن $k$ یال اهمیت دارد.**
# ورودی
در خط اول ورودی سه عدد $n$، $m$ و $k$ آمده است.
در $m$ خط بعدی دو عدد $v$ و $u$ آمده است، که نشان میدهد یک یال بین رئوس $v$ و $u$ وجود دارد.
$$3 \le n \le 1\ 000$$
$$n-1 \le m < {n \choose 2}$$
$$1 \le v, u \le n$$
$$m + k \le {n \choose 2}$$
$$1 \le k$$
**تضمین میشود گراف ورودی، گرافی همبند و ساده است.**
# خروجی
در خروجی باید باقیمانده تعداد روشهای خواسته شده بر $10^{9} + 7$ را چاپ کنید.
## ورودی نمونه ۱
```
4 3 2
1 2
2 3
3 4
```
## خروجی نمونه ۱
```
6
```
<details>
<summary>توضیحات مثال</summary>
حالت های معتبر به شکل زیر هستند:
$${(1, 3), (1, 4)}$$
$${(1, 3), (2, 4)}$$
$${(1, 4), (2, 4)}$$
$${(1, 4), (1, 3)}$$
$${(2, 4), (1, 3)}$$
$${(2, 4), (1, 4)}$$
هر سطر نشان دهندهٔ یک حالت از انجام $k$ مرحله است. ($(i, j)$ نمایانگر کشیدن یال بین دو رأس $i$ و $j$ است و یالها را در هر سطر از چپ به راست اضافه میکنیم)
</details>
## ورودی نمونه ۲
```
3 2 1
1 2
1 3
```
## خروجی نمونه ۲
```
1
```
تنها میتوان یال $(2, 3)$ را اضافه کرد.
گراف افکار
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
ابواسحاق پس از ترمیم رشتهٔ افکار خود، آغاز به کشت خیار کرد! امّا در این بین، علفهای هرز مانع کسب و کار او شدند. برای همین، شروع به حذف کردن علفهای هرز کرد.
مزرعهٔ او به شکل جدولی $n\times m$ است که دارای $n$ سطر با شمارههای $0$ تا $n - 1$ از بالا به پایین و $m$ ستون با شمارههای $0$ تا $m - 1$ از چپ به راست میباشد. در ابتدا $k$ علف هرز در مزرعه وجود دارد. او در هر مرحله میتواند یکی از عملیاتهای زیر را انجام دهد:
+ یک علف هرز از خانهٔ $(i, j)$ را با دست بکَنَد. در این صورت $w_{i, j}$ انرژی مصرف میکند. (برای خم شدن و کندن علف هرز)
+ پا روی خانهٔ $(i, j)$ بگذارد، در این صورت یکی از علفهای هرز موجود در آن خانه از بین رفته و یک علف هرز به خانهی $((i + 1)\mod n, j)$ و علف هرزی دیگر به خانهی $(i, (j + 1)\mod m)$ اضافه میشود. توجه کنید که در این عملیات هیچ انرژیای از او کم نمیشود ($a\mod b$ برابر با باقی مانده تقسیم $a$ بر $b$ است).
حال او وضعیت اولیهٔ مزرعه و علفهای هرز را به شما میدهد و از شما میخواهد که کمترین انرژی لازم برای از بین بردن تمامی علفهای هرز مزرعه را محاسبه کنید.
# ورودی
در خط اول دو عدد $n$ و $m$ و $k$ داده میشود.
در هر یک از $n$ سطر بعدی $m$ عدد آمده است که عدد $j$ ام در سطر $i$ ام مقدار $w_{i, j}$ را مشخص میکند.
در خط $i$ ام از $k$ خط بعدی دو عدد $x_i$ و $y_i$ آمده که نشان میدهد علف هرز $i$ ام در خانه $(x_i, y_i)$ است.
$$ 1 \le n, m \le 1\ 000 $$
$$1 \le k \le 1\ 000$$
$$ 0 \le x_i < n $$
$$ 0 \le y_j < m $$
$$ 1 \le w_{i, j} \le 1\ 000$$
**دقت کنید ممکن است در ابتدا در یک خانه بیش از یک علف هرز وجود داشته باشد.**
# خروجی
در یک خط عدد خواسته شده را چاپ کنید.
## ورودی نمونه ۱
```
2 2 1
3 1
1 1
0 0
```
## خروجی نمونه ۱
```
2
```
در ابتدا یک علف هرز در خانهٔ $(0 ,0)$ وجود دارد. ابواسحاق روز آن پا گذاشته و در نتیجه در هر یک از خانههای $(1 ,0)$ و $(0 ,1)$ یک علف هرز بوجود میآید. سپس هر کدام از علفهای هرز جدید را با دست میکند و در مجموع ۲ واحد انرژی از دست میدهد.
## ورودی نمونه ۲
```
3 3 2
7 5 1
4 3 1
1 2 1
0 1
1 0
```
## خروجی نمونه ۲
```
8
```
در ابتدا دو علف هرز یکی در خانه $(0,1)$ و دیگری در خانه $(1,0)$ موجود است، ابواسحاق با پا گذاشتن روی این دو علف آنها را به صورت $(0,2)$، $(1,1)$، $(1,1)$ و $(2,0)$ درمیآورد (توجه کنید دو علف هرز در خانه $(1,1)$ موجود است) سپس تمامی آنها را با دست میکند که در مجموع از او ۸ واحد انرژی میگیرد همچنین میتوان ثابت کرد این مقدار کمینه انرژی لازم است.
علف هرز
+ محدودیت زمان: ۲ ثانیه
+ محدودیت حافظه: ۵۱۲ مگابایت
----------
بعد از آنکه ابواسحاق از دست علفهای هرز راحت شد، دشمنانش به دلیل موفقیتش در خیار کاری، به او حسادت کردند و تصمیم گرفتند یکی از مزارع او را تخریب کنند.
مزرعه ابواسحاق به صورت یک جدول $1 \times n$ است که خانههایش از چپ به راست به ترتیب از ۱ تا $n$ شماره گذاری شدهاند و در خانه $i$ اُم آن $ a_i $ خیار کاشته شده است. مزرعهٔ او $ q $ روز فعالیت میکند. در **ابتدای** هر روز، به تعداد خیارهای خانهٔ $i$ اُم $b_i$ تا اضافه میشود و در **انتهای** هر روز، یکی از دو اتفاق زیر رخ میدهد:
+ ابواسحاق نیاز به محاسبهٔ سود خود پیدا میکند و از شما مجموع تعداد خیارهای موجود در خانههای بازهی $[l, r]$ را میپرسد.
+ دشمنان ابواسحاق خانهٔ $x$ اُم را آتش میزنند و این آتش از هر دو طرف با سرعتی برابر شروع به پیشروی میکند و تا وقتی که به یک آلارم نرسد، متوقف نمیشود؛ پس از رسیدن آتش به هر خانه، تعداد خیارهای آن نصف میشود (مقدار جزء صحیح آن مورد نظر است). توجه کنید هنگامی که یک طرف آتش به یک آلارم برسد بلافاصله آتش از هر دو طرف خاموش میشود (دقت کنید خانهای که در آن آلارم است آتش نمیگیرد). بعد از پایان آتش سوزی ابواسحاق یک آلارم در خانهٔ $x$ قرار میدهد. کل فرآیند پیشروی آتش در یک روز انجام میشود و به روزهای بعدی کشیده نمیشود.
**در ابتدا فقط در خانههای $0$ و $ n + 1 $ یک آلارم وجود دارد** (یکی قبل از خانه اول مزرعه و یکی بعد از خانه آخر آن) و بقیه خانهها بدون آلارم هستند. برای هر اتفاق از نوع یک، مجموع تعداد خیارها را خروجی دهید.
# ورودی
در خط اول دو عدد $n$ و $q$ میآید که به ترتیب تعداد خانههای مزرعه ابواسحاق و تعداد روزهایی است که مزرعه فعالیت میکند.
در خط دوم $n$ عدد میآید که عدد $i$ اُم، برابر با $a_i$ است.
در خط سوم نیز $n$ عدد میآید که عدد $i$ اُم، برابر با $b_i$ یا همان نرخ رشد خانهٔ $i$ ام است.
سپس در هر خط از $q$ خط بعدی ابتدا $t$ یا همان نوع اتفاق آمده که یکی از دو حالت زیر را دارد:
+ اگر $t = 1$ باشد آنگاه اتفاق از نوع اول است و در ادامه همان خط دو عدد $l$ و $r$ ورودی داده میشود.
+ اگر $t = 2$ باشد آنگاه اتفاق از نوع دوم است و در ادامه همان خط عدد $x$ ورودی داده میشود.
*تضمین میشود مقدار $x$ برای هرکدام از $q$ روز متفاوت است.*
$$ 1 \le n \le 100\ 000 $$
$$ 1 \le q \le 300\ 000 $$
$$ 1 \le l, r, x \le n $$
$$ 1 \le a_i, b_i \le 1\ 000\ 000 $$
# خروجی
به ازای هر اتفاق نوع اول مقدار خواسته شده را در یک سطر خروجی دهید.
## ورودی نمونه ۱
```
7 4
10 10 10 10 10 10 10
1 3 4 2 3 2 4
2 2
1 1 4
2 4
1 3 7
```
## خروجی نمونه ۱
```
40
77
```
خیارهای اولیه مزرعه به صورت $[10 ,10 ,10 ,10 ,10 ,10 ,10]$ است.
در ابتدای روز اول خیارها رشد کرده و مزرعه به صورت $[11, 13, 14, 12, 13, 12, 14]$ درمیآید، در انتهای روز اول خانه دوم آتش گرفته در نتیجه آتش پیشروی کرده تا به یک آلارم برسد(در این روز آتش قبل از آلارم خانه $0$ ام متوقف میشود) در نتیجه مقدار خیارها در خانههای $1,2,3$ نصف میشود و مزرعه در انتهای روز به صورت $[5, 6, 7, 12, 13, 12, 14]$ درمیآید.
در ابتدای روز دوم با رشد خیارها مزرعه به صورت $[6, 9, 11, 14, 16, 14, 18]$ درمیآید. سپس جمع تعداد خیارهای خانههای $1,2,3,4$ را خروجی میدهیم.
در روز سوم مانند روزهای قبل پس از رشد داریم $[7, 12, 15, 16, 19, 16, 22]$ و با آتش گرفتن خانه چهارم و پیشروی آن تا رسیدن به اولین آلارم از یک سمت، تعداد خیارهای خانههای $3,4,5$ نصف خواهد شد و مزرعه به صورت $[7, 12, 7, 8, 9, 16, 22]$ درمیآید. روز چهارم نیز به همین ترتیب سپری خواهد شد.
خیار سوزی
+ محدودیت زمان: ۳ ثانیه
+ محدودیت حافظه: ۵۱۲ مگابایت
----------
ابواسحاق که از شر دشمنانش جان سالم به در برده بود، تصمیم گرفت جشنی عظیم برگزار کند. آقا تیزی که قبل از شروع جشن به آنجا رسیده بود، تصمیم گرفت در آماده کردن تزئینات به ابواسحاق کمک کند.
برای همین، ابواسحاق $k$ ریسه به آقا تیزی داد. هر ریسه شامل $n$ لامپ رنگی متوالی است. رنگ لامپها در یک ریسه، جایگشتی از اعداد ۱ تا $n$ است؛ سپس از او خواست تا از ابتدا و انتهای هر ریسه تعدادی لامپ حذف کند (ممکن است هیچ لامپی حذف نشود، امّا همهٔ لامپها حذف نمیشوند)، با این شرط که در ریسههای جدید به ازای هر دو ریسه مانند $a$ و $b$، هر رنگ که در ریسهٔ $a$ آمده در ریسهٔ $b$ نیز آمده باشد.
آقا تیزی که میخواهد زیباترین تزئینات را انجام دهد، از شما میخواهد که تعداد روشهای مختلف انجام این کار را به او بگویید تا بهترین را انتخاب کند (دو روش متفاوت هستند، اگر در ریسهای لامپی حذف شود که در دیگری حذف نشده باشد).
# ورودی
در خط اول ورودی دو عدد $n$ و $k$ آمده است که به ترتیب تعداد لامپهای هر ریسه و تعداد ریسهها را مشخص میکند.
در هر یک از $k$ خط بعدی، $n$ عدد داده شده است که عدد $j$ اُم در سطر $i$ اُم برابر با $a_{i,j}$ است. ($a_{i,j}$ نشان دهندهٔ رنگ لامپ $j$ اُم در ریسهٔ $i$ اُم است)
$$2 \le k \le 1\ 000\ 000$$
$$1 \le n \times k \le 1\ 000\ 000$$
$$1 \le a_{i,j} \le n$$
**تضمین میشود رنگ لامپهای موجود در یک ریسه جایگشتی از اعداد $1$ تا $n$ است.**
# خروجی
در تنها خط خروجی تعداد حالات خواسته شده را چاپ کنید.
# مثال
## ورودی نمونه ۱
```
3 2
1 3 2
2 1 3
```
## خروجی نمونه ۱
```
5
```
<details>
<summary>توضیحات مثال</summary>
۵ حالت ممکن به این ترتیب است:
+ از ریسه اول دو لامپ آخر و از ریسه دوم لامپ اول و آخر حذف شود
+ از ریسه اول دو لامپ اول و از ریسه دوم دو لامپ آخر حذف شود.
+ از ریسه اول لامپ اول و آخر و از ریسه دوم دو لامپ اول حذف شود.
+ از ریسه اول لامپ آخر و از ریسه دوم لامپ اول حذف شود.
+ از هیچ یک از ریسهها لامپی حذف نشود.
</details>
## ورودی نمونه ۲
```
3 3
1 2 3
2 1 3
3 2 1
```
## خروجی نمونه ۲
```
5
```
<details>
<summary>توضیحات مثال</summary>
۵ حالت ممکن به این ترتیب است:
+ پس از عملیات حذف، ریسههای ۱ و ۲ و ۳ به ترتیب به شکل $[1]$ و $[1]$ و $[1]$ درمیآیند.
+ پس از عملیات حذف، ریسههای ۱ و ۲ و ۳ به ترتیب به شکل $[2]$ و $[2]$ و $[2]$ درمیآیند.
+ پس از عملیات حذف، ریسههای ۱ و ۲ و ۳ به ترتیب به شکل $[3]$ و $[3]$ و $[3]$ درمیآیند.
+ پس از عملیات حذف، ریسههای ۱ و ۲ و ۳ به ترتیب به شکل $[1,2]$ و $[2,1]$ و $[2,1]$ درمیآیند.
+ پس از عملیات حذف، ریسههای ۱ و ۲ و ۳ به ترتیب به شکل $[1,2,3]$ و $[2,1,3]$ و $[3,2,1]$ درمیآیند.
</details>
لامپهای رنگارنگ
+ محدودیت زمان: ۲ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
میهمانها که از جشن با شکوه ابواسحاق بسیار لذت برده بودند تصمیم گرفتند هر یک نامهای برای تشکر، به او بفرستند. او نیز برای ثبت این خاطرهی زیبا بنا به ساختن رشتهای زیبا کرد.
ابواسحاق $n$ نامه، $s_1, s_2, ..., s_n\ $ از حروف کوچک انگلیسی دریافت کرده و نامه $i$ام را $c_i$ واحد دوست دارد.
زیبایی رشته $T$ برای او به صورت زیر تعریف میشود (تابع $occurs(s, t)$ تعداد تکرارهای رشته $t$ در رشته $s$ را مشخص میکند):
$$b(T) = \dfrac{\sum^{n}_{i=1} c_i * occurs(T, s_i)}{|T|}$$
ابواسحاق که میخواهد زیباترین رشته را بسازد، لازم است بیشترین مقدار $b(T)$ را به ازای همه رشتههای به طول $10^{100}$ محاسبه کند.
او که پس از جشن بسیار خسته شده از شما میخواهد تا این مقدار را برایش محاسبه کنید.
# ورودی
در خط اول ورودی $n$ که نمایانگر تعداد رشتهها است آمده است. در خط بعدی $n$ عدد $c_i$ آمدهاند. سپس در $n$ خط بعدی، در هر خط $s_i$ میآید.
$$1 \le \sum^{n}_{i=1} |s_i| \le 500$$
$$1 \le c_i \le 10^9$$
# خروجی
در تنها خط خروجی مقدار خواسته شده را چاپ کنید. در صورتی که جواب شما $y$ باشد و جواب واقعی $x$ باشد؛ جواب شما مورد قبول است اگر شرط $\dfrac{|x-y|}{x} \le 10^{-6}$ برقرار باشد.
# مثال
## ورودی نمونه ۱
```
1
10
aa
```
## خروجی نمونه ۱
```
10.000000
```
در این نمونه به ازای رشته $T$ که از $10^{100}$ تا کاراکتر `a` تشکیل شده، مقدار $F$ برابر با $10 - 10^{-100}$ است که با دقت شش رقم اعشار ۱۰ میشود.
## ورودی نمونه ۲
```
4
2 3 4 5
abb
bba
aab
baa
```
## خروجی نمونه ۲
```
3.500000
```
رشته خیلی بزرگ
+ محدودیت زمان: ۴ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
ابواسحاق پس از خواندن تمام نامهها، به یک دعوتنامه بَر خورد. او که بسیار کنجکاو شده بود به آدرس داخل دعوتنامه رفت و سَر از جزیرهٔ آدمخوارها درآورد! آنها ابواسحاق را تهدید کردند که اگر میخواهد او را نخورند، باید جای خرگوشهای جزیره را برایشان پیدا کند. او هم که خیلی ترسیده بود، از شما کمک خواست تا جای خرگوشها را پیدا کنید. سوال آدم خوارها به صورت زیر است:
تعدادی خرگوش روی محور $x$ ها ایستادهاند. خرگوشها با اعداد ۱ تا $n$ شمارهگذاری شدهاند و خرگوش شماره $i$ ابتدا در موقعیت مکانی $a_i$ قرار دارد. یک عملیات قرینهسازی روی خرگوش شماره $i$ به صورت زیر انجام می شود:
+ با احتمال برابر، یکی از خرگوشهای $i+1$ یا $i-1$ انتخاب میشود (اندیسها دایره ای هستند؛ به عبارت دیگر اگر عملیات روی خرگوش شماره ۱ انجام شود، یکی از خرگوشهای $2$ یا $n$ انتخاب میشوند).
+ موقعیت خرگوش شماره $i$ نسبت به خرگوش انتخاب شده قرینه میشود.
آدمخوارها به ما یک ترتیب از عملیاتهای قرینهسازی را میدهند و ما $k$ بار پشت سر هم و به همین ترتیب، این عملیاتها را انجام میدهیم. حال شما باید به ازای هر خرگوش باقیمانده امیدریاضی مکانش را نسبت به $10^9 + 7$ به دست آورید.
# ورودی
در خط اول ورودی، تعداد خرگوشها، $n$ میآید. سپس در خط دوم، دنباله $a_1 , a_2 , ... , a_n $ موقعیت مکانی اولیه خرگوشها می آیند.
در خط بعد، دو عدد $m$ و $k$ ورودی داده میشوند.
در خط آخر، دنباله عملیاتها، $b_1 , b_2 , ... , b_m $ ورودی داده میشود.
$$ 3 \le n \le 200\ 000 $$
$$ 0 \le a_i \le 10^9 + 6 $$
$$ 1 \le m \le 200\ 000 $$
$$ 1 \le k \le 10^{18} $$
# خروجی
در خروجی یک دنباله به طول $n$، شامل امید ریاضی مکان نهایی خرگوشها باقیمانده بر $10^9 + 7$ را چاپ کنید.
## ورودی نمونه ۱
```
3
1 2 3
3 2
2 1 3
```
## خروجی نمونه ۱
```
4
5
6
```
## ورودی نمونه ۲
```
4
1 0 1 0
2 3
2 3
```
## خروجی نمونه ۲
```
1
0
1
0
```