+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
*****
تعداد $n$ سرمایهدار و سرمایهدار سابق برای احوالپرسی و تفکر و تحقیق و سرمایهگذاری به دور هم گردآمدند. ابتدا آنها پس از مقداری احوالپرسی متوجه شدند که سرمایهداران سابق، ورشکسته شده و تازه بدهی هم دارند!! سپس آنها با مقداری تفکر به این نتیجه رسیدند که عجب دوره و زمانهی بدی شده است و بعد از آن برای این که بدانند که دقیقا چقدر دوره و زمانهی بدی شده است، دست به مقداری تحقیق زدند. آنها تعداد زوج مرتبهایی از افراد را شمردند که اختلاف سرمایهی اولی با دومی از جمع سرمایهی هر دو بیشتر است؛ یعنی به ازای زوج مرتب $(a, b) $، $a - b$ از $a + b$ بیشتر است. در نهایت هم آنها، با توجه به هدف جلسه که در خط اول گفته شد، تصمیم گرفتند که مقداری سرمایهگذاری کنند؛ اما از روی ناچاری و نبود موقعیت مناسب تصمیم گرفتند که در صورت شمارش تعداد جفتهایی که در بالا گفتهشدهاست، بر روی شما سرمایهگذاری کنند!
# ورودی
در سطر اول ورودی عدد $n$ آمده است که نمایانگر تعداد سرمایهدارها میباشد.
سپس در خط بعدی $n$ عدد میآید که عدد $i$ام، $a_i$، نمایانگر سرمایهی فرد $i$ میباشد. دقت کنید که سرمایهی یک فرد میتواند منفی یا صفر باشد.
$$ 1 \le n \le 1 \ 000 \ 000 $$
$$ -10^9 \le a_i \le 10^9 $$
# خروجی
در تنها سطر خروجی تعداد زوج مرتبهایی را بشمارید که اختلاف اولی با دومی از جمعشان بیشتر است. دقت کنید که زوج $(a, b)$ با زوج $(b,a)$ متفاوت است.
# مثال
## ورودی نمونه ۱
```
4
-2 3 3 0
```
## خروجی نمونه ۱
```
3
```
زوجهای مورد نظر در این نمونه برابر است با:
(۲-, ۳)،(۲-, ۰)،(۲-, ۳)
زوج سرمایهدار
+ محدودیت زمان: ۲ ثانیه
+ محدودیت حافظه: ۱۲۸ مگابایت
*****
در جمعی $n$ نفر مشغول بازی اسمفامیل هستند! در این بازی $m$ موضوع داریم(مثل اسم، فامیلی، غذا، نام شهر و...). و برای هر موضوع نیز تعدادی کلمهی مجاز داریم! همچنین این بازی متشکّل از تعدادی مرحله است. در هر مرحله یکی از حروف الفبا انتخاب میشود؛ سپس تمام افراد باید به ازای هر موضوع، در کاغذ خود **یک** کلمه بنویسند که با حرف متناظر آن مرحله شروع میشود.
پس از پایان هر مرحله، به هر کس امتیازی میرسد (به ازای هر موضوع امتیاز جداگانهای به هر فرد اضافه میشود) چنان چه در موضوعی آن شخص کلمهای ننوشته باشد و یا کلمهای نوشته باشد که مجاز نباشد و یا با آن حرف شروع نشود، امتیاز آن موضوع را دریافت نمیکند؛ اگر کلمهای که در این موضوع نوشته است، توسّط بازیکن دیگری نیز نوشته شده باشد، از این موضوع ۵ امتیاز میگیرد و اگر فقط او چنین کلمهای در این موضوع نوشته باشد، ۱۰ امتیاز دریافت خواهد کرد.
مثلن اگر تنها دو موضوع «اسم» و «فامیل» داشته باشیم، حرفی که برای این مرحله انتخاب میشود a باشد و سه بازیکن داشته باشیم که هر یک به شرح زیر کلماتی را در کاغذشان نوشته باشند؛
| بازیکن | اسم | فامیل |
|:------:|:---:|:-----:|
|۱| ali | ahadi|
|۲|ali | akbari |
|۳| | askari|
«اسم»های مجاز: ali, ahmad
«فامیل»های مجاز: akbari, askari
در این بازی، بازیکن یک ۵ امتیاز، بازیکن دو ۱۵ امتیاز و بازیکن سه ۱۰ امتیاز خواهند گرفت.
در ورودی جزییات بازی به شما داده میشود و شما باید امتیاز نهایی هر بازیکن را در خروجی چاپ کنید.
# ورودی
در خط اوّل ورودی سه عدد آمده که با space از هم جدا شدهاند. ابتدا $n$ تعداد بازیکنها، سپس $m$ تعداد موضوعات و سپس $k$ تعداد مرحلهها.
در $m$ خطِ بعد، کلمات مجاز هر موضوع آمدهاند؛ در خط $i$ام کلمات مجاز موضوع $i$ام میآیند که با space از هم جدا شدهاند.
ادامهی ورودی $k$ بخش دارد، بخش $i$ام نمایانگر اطّلاعات مرحلهی $i$ام است.
اطّلاعات هر مرحله شامل $n + 1$ خط است؛ در خط اوّل حرفی که برای آن مرحله انتخاب شده میآید و سپس در $n$ خط بعد، در هر خط $m$ کلمه میآید که -باز هم- با space از هم جدا میشوند. کلمهی $j$ام در خط $i$ام نمایانگر کلمهای است که بازیکن $i$ام برای موضوع $j$ام در این مرحله روی کاغذش مینویسد. در صورتی که بازیکنی برای موضوعی هیچ کلمهای ننوشته باشد، به جای آن کلمه عبارت "EMPTY" در ورودی میآید.
لازم به ذکر است که هر کلمه متشکّل از حداکثر ۱۰ کاراکتر است و حرفِ متناظر هر مرحله از بازی و تمام کاراکترهای کلمات از بین حروف کوچک الفبای انگلیسی انتخاب میشوند. همچنین تعداد مراحل بازی حداکثر ۲۶ و تعداد بازیکنها و موضوعات حداکثر ۵۰ عدد خواهد بود. تعداد کلمات مجاز به ازای هر موضوع نیز از ۱۰۰ کلمه بیشتر نخواهد شد.
# خروجی
در تنها خط خروجی $n$ عدد چاپ کنید که عدد $i$ام امتیاز نهایی بازیکن $i$ام است. اعداد باید با space از هم جدا شده باشند.
# مثال
## ورودی نمونه ۱
```
4 3 2
karim rahim asghar ahmad zahra zeynab
zakeri karimi rahimi akbari ahmadi zahiri
zebra zaloo moorcheh zarrafeh soosk palang ankaboot rasoo
z
EMPTY zahiri EMPTY
zeynab zakeri zebra
karim zahiri zebra
zohreh EMPTY zaloo
a
ahmad ahmadi ankaboot
asghar akbari ankabtoo
rahim rahimi rasoo
EMPTY EMPTY asb
```
## خروجی نمونه ۱
```
35 45 10 10
```
در مرحلهی اوّل امتیازاتی که افراد میگیرند به این شکل است:
بازیکن ۱: ۵ امتیاز
بازیکن ۲: ۲۵ امتیاز
بازیکن ۳: ۱۰ امتیاز
بازیکن ۴: ۱۰ امتیاز
در مرحلهی دوم نیز امتیازات به این شکل خواهند بود:
بازیکن ۱: ۳۰ امتیاز
بازیکن ۲: ۲۰ امتیاز
بازیکن ۳: ۰ امتیاز
بازیکن ۴: ۰ امتیاز
اسفا میل
+ محدودیت زمان: ۲ ثانیه
+ محدودیت حافظه: ۱۲۸ مگابایت
*****
اخیرا آقای ماهر دستگاهی اختراع کرده که طبق ادّعایش میتواند زمینهای ناهموار را هموار کند. اگر ادّعای او درست باشد، اختراع وی، عصر جدیدی را در صنعت صافسازی رقم خواهد زد. حال بزرگان این صنعت جمع شدهاند تا ببیند ادّعای آقای ماهر درست است یا نه!
آقای ماهر برای این که درست بودن دستگاهش را به دیگران ثابت کند، میخواهد یک کوهستان را با استفاده از دستگاهش هموار کند. کوهستانی که او برای این کار انتخاب کرده است، به شکل یک مستطیل $n \times m$ است. یعنی کوهها در $n$ سطر قرار دارند و هر سطر شامل $m$ کوه است. (کوههای هر سطر و هر ستون در یک خط قرار گرفتهاند) هر کوه ارتفاعی صحیح و نامنفی نیز دارد؛ ارتفاع کوه $j$ام از سطر $i$ام کوهستان را با $A_{i, j}$ نشان میدهیم.
دستگاه آقای ماهر در هر مرحله ۴ ورودی میگیرد و قسمتی از کوهستان را طبق آن ۴ ورودی هموارتر میکند. ورودیهایی که دستگاه میگیرد در یکی از دو قالب زیر هستند:
1. R $l$ $r$ $k$
2. C $l$ $r$ $k$
در حالت اوّل، ارتفاع هر کوهی که در یکی از سطرهای $l$ تا $r$ (شامل این دو سطر) باشد، تقسیم بر $k$ خواهد شد($1\leq l \leq r \leq n$). در حالت دوم نیز همین اتّفاق برای هر کوهی که در یکی از ستونهای $l$ تا $r$ (شامل این دو ستون) وجود دارد میافتد($1 \leq l \leq r \leq m$). چنان چه ارتفاع جدید هر کوه عددی ناصحیح باشد، بر اثر عوامل طبیعی از ارتفاع کوه آن قدر کاسته میشود تا به اوّلین عدد صحیح کوچکتر از خودش برسد!
مثلن اگر ارتفاع کوهی $9$ باشد و عملیاتی با $k=4$ روی آن اعمال شود، ارتفاع آن ابتدا برابر $2.25$ میشود و سپس تبدیل به $2$ میشود. امّا اگر عملیاتی به ازای $k=3$ روی آن اعمال شود، ارتفاعش برابر $3$ میشود.
آقای ماهر در زمینهی محاسبات ماهر نیست؛ لذا ارتفاع کوههای کوهستان و عملیاتی که قرار است با دستگاه انجام دهد را به شما میگوید؛ در ازای این دادهها نیز میخواهد ارتفاع نهایی کوهها را در صورتی که دستگاه درست کار کند، به او بگویید.
# ورودی
در سطر اوّل ورودی دو عدد $n$ و $m$ میآیند.
در هر یک از $n$ سطر بعد، $m$ عدد آمده است. عدد $j$ام در $i$امین سطر برابر $A_{i, j}$ است.
سپس در یک خط عدد $q$ میآید که تعداد درخواستهاست.
در هر یک از $q$ سطر بعد، یکی از ورودیهای سوال در قالبی که گفته شد قرار دارد.
$$1 \leq n, m \leq 1\ 000$$
$$1 \leq q \leq 10\ 000$$
$$1 \leq k, A_{i, j} \leq 1\ 000\ 000\ 000$$
# خروجی
در خروجی ارتفاع نهایی کوهها را چاپ کنید.
خروجی شما باید از $n$ سطر تشکیل شده باشد که هر کدام از آنها شامل $m$ عدد هستند. .عدد $j$ام از سطر $i$ام برابر با ارتفاع نهایی کوه $j$ام از سطر $i$ام کوهستان خواهد بود.
# مثال
## ورودی نمونه ۱
```
2 3
1 2 3
4 5 6
1
C 2 3 2
```
## خروجی نمونه ۱
```
1 1 1
4 2 3
```
## ورودی نمونه ۲
```
3 3
10 20 3
15 1000 60
16 10 20
4
R 2 3 4
C 1 2 2
R 1 2 3
R 2 2 5
```
## خروجی نمونه ۲
```
1 3 1
0 8 1
2 1 5
```
صافکن
+ محدودیت زمان: ۳ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
*****
شرکت گذشتهسازان فعلی به یک مشکل جدی برنامهنویسی خورده است و قصد استخدام یک برنامهنویس را دارد؛ از این رو آنها مشکلشان را به عنوان یک سوال در اینجا گذاشتند تا افرادی که واقعا قادر به حل مشکلشان هستند را بیابند:
این شرکت $n$ کار دارد (آنها را با اعداد ۱ تا $n$ شمارهگذاری میکنیم) که انجام دادن کار $i$ام، $t_i$ روز طول خواهد کشید. شما باید برنامهای بنویسید که برنامهای برای انجام دادن این کارها چاپ کند که کمترین ضرر را داشته باشد. فقط قبل از این که دست به کد شوید به نکات زیر توجه کنید:
۱- هر روز را میتوان به انجام دادن فقط یک کار اختصاص داد.
۲- تا زمانی که کار نیمهکارهای وجود دارد نمیتوان کار دیگری را شروع کرد. در نتیجه در هر لحظه حداکثر یک کار نیمهکاره وجود دارد؛ به عبارت دیگر، زمانی که یک کار را شروع میکنیم، تا زمان پایان یافتن آن نباید کار دیگری شروع شود.
۳- تعدادی از کارها هستند که پیشنیاز یک سری دیگر از کارها هستند؛ یعنی تا زمانی که پیشنیاز یک کاری به طور کامل انجام نشود، نمیتوان سراغ خود آن کار رفت.
۴- بعضی از کارها نسبت به هم «فوری» هستند؛ یعنی هر چقدر فاصلهی تمام شدنشان از هم کمتر باشد، بهتر است. در نتیجه به اندازهی فاصلهی تمام شدن این دو کار ما ضرر خواهیم کرد.
۵- بعضی از کارها نسبت به هم «نافوری» هستند؛ یعنی بهتر است که حداقل ۱۵ روز بین تمام شدن این کارها فاصله باشد. در نتیجه اگر فاصلهی تمام شدن این دو کار را $d$ در نظر بگیریم، به اندازهی $max(0, 15 - d) $ ضرر خواهیم کرد.
**در این سوال، بسته به تعداد تستهایی که درست پاسخ دهید نمره میگیرید. برنامهی شما هرچه بهینهتر باشد، نمرهی بیشتری دریافت خواهید کرد.**
# ورودی
در سطر اول ورودی چهار عدد $n$، $m$، $f$ و $h$ آمدهاست که به ترتیب نمایانگر تعداد کارها، تعداد جفت کارهایی که اولی پیشنیاز دومی است، تعداد جفت کارهایی که نسبت به هم «فوری» هستند و تعداد جفت کارهایی که نسبت به هم «نافوری» هستند میباشد.
سپس در سطر بعدی $n$ عدد آمده است که عدد $i$ام نمایانگر $t_i$ میباشد.
بعد از آن، در $m$ سطر بعدی، در هر سطر، به ترتیب دو عدد $a$ و $b$ آمده است که نمایانگر این است که کار شمارهی $a$ باید قبل از کار شمارهی $b$ انجام شود.
سپس در $f$ سطر بعدی، در هر سطر، دو عدد $a$ و $b$ آمده است که نمایانگر این است که کار شمارهی $a$ و $b$ نسبت به هم «فوری» هستند.
و در نهایت در $h$ سطر بعدی، در هر سطر، دو عدد $a$ و $b$ آمده است که نمایانگر این است که کار شمارهی $a$ و $b$ نسبت به هم «نافوری» هستند.
$$ 1 \le n, m, f, h, t_i \le 15 $$
# خروجی
در تنها سطر خروجی کمترین مقدار ضرر را چاپ کنید. اگر راهی برای انجام دادن کارها با توجه به شرایط پیشنیازی وجود ندارد در یک خط عبارت "varshekast shodin" را چاپ نمایید.
# مثال
## ورودی نمونه ۱
```
3 2 1 1
1 2 3
1 2
2 3
1 2
2 3
```
## خروجی نمونه ۱
```
14
```
در نمونهی بالا، با توجه به شرایط پیشنیازی میتوان فهمید که تنها حالتی که شرایط پیشنیازی در آن رعایت شود حالت ۱،۲،۳ است که مقدار ضرر این حالت با توجه به نکات زیر حساب میشود:
کارهای ۱ و ۲ فوری هستند و فاصلهی بین پایان این دو کار ۲ روز میباشد؛ پس دو واحد ضرر ایجاد شده است.
کارهای ۲ و ۳ نافوری هستند و فاصلهی بین پایان این دو کار ۳ روز میباشد؛ پس به اندازهی ۳ - ۱۵ واحد ضرر ایجاد میکنند که با ۲ واحد ضرر قبلی میشود ۱۴ واحد ضرر.
برنامهنویس برنامه نویس!
+ محدودیت زمان: ۲ ثانیه
+ محدودیت حافظه: ۵۱۲ مگابایت
----------
همانطور که میدانید، این روزها روزهای خاصی در ایران است. همه جا همه در حال بحث و گفتوگو راجع به انتخابات هستند و دغدغههای جمعی بزرگی بین همهی مردم ایران بوجود آمده. اخیراً بحثها به داخل شرکتها و در زمان کاری هم رسیده؛ تعداد زیادی از شرکتهای حوزه IT جلسات برنامهریزی شده و نشدهای برای بحث سر انتخابات برگزار میکنند. وقتی موضوعی در شرکتهای برنامهنویسی وارد میشود، همیشه شکل و فرم خودش را از دست میدهد و با روشهای جدید، ابعاد جدیدی از موضوع بررسی میشود. برای مثال، همین که برنامهنویسها راجع به انتخابات بحث میکنند، موضوع جدیدی برای بحث شده است! حتی این موضوع که برنامهنویسها راجع به برنامهنویسهایی که راجع به انتخابات بحث میکنند، بحث میکنند، موج جدیدی از بحثها را بین برنامهنویسان راه انداخته است...
شکل زیر نمای بالا از جلسهای ۴ نفره است که سر انتخابات بحث میکنند. ۴ طرف میز، صندلی برنامهنویسان وجود دارد و جلوی هر فرد، تبلتی رومیزی وجود دارد که عکس یکی از نامزدهای انتخابات در آن مشخص است. (بدلیل حقیقتاً بیطرف بودن Quera در انتخابات، عکس نامزدها سانسور شده و بجای آنها بخشی از یک آباژور قرار داده شده است.)
```
----
| |
| |
----
--------------------
| | __ | |
| |/__\| |
| | || | |
| | || | |
| ------ |
| |
------ ------
----| __ | | __ |----
| ||/__\| |/__\|| |
| || || | | || || |
----| || | | || |----
------ ------
| |
| ------ |
| | __ | |
| |/__\| |
| | || | |
| | || | |
--------------------
----
| |
| |
----
```
به این نوع بحث، بحث سطح ۰ میگوییم. (فرض کنید داخل اتاقی بروید و ببینید که ۴ نفر خیلی جدی راجع به تعدادی آباژور بحث میکنند؛ حقیقتاً بحث سطح صفریست.)
**یک شِما (Schema) از بحث سطح ۱ را میتوانید در [اینجا](http://bayanbox.ir/view/6992899914868998408/oup.txt) ببینید**؛ به این صورت است که ۴ برنامهنویس پشت میز جلسات نشستهاند و راجع به برنامهنویسانی که بحث سطح ۰ دارند، بحث میکنند. روی تبلت رومیزی آنها، شِمایی از این برنامهنویسان موجود است. در کل بحث سطح $x$ بین ۴ برنامهنویس صورت میگیرد که راجع به بحث سطح $x - 1$ حرف میزنند. شکل از بالای آن نیز به شکل بحث سطح $x-1$ است با این تفاوت که ابعاد شکل بزرگ شده که یک شکل از بالای بحث سطح ۰ در کوچکترین تبلتهای آن (بجای آباژورها) قرار بگیرد.
هدف این است که با ورودی گرفتن عدد $n$، شکل از بالای بحث سطح $n$ را در خروجی استاندارد چاپ کنید. اما با توجه به خیلی سطح بالا بودن برخی بحثها، شکل از بالای آنها بسیار بزرگ میشود و هنوز جامعهی برنامهنویسان به این سطح نرسیده که از آنها بخواهیم که آن را خروجی دهند؛ از این رو، به شما یک مختصات $r$ و $c$ (که این دو اعدادی طبیعیاند) نیز داده میشود که یعنی کافیست به اندازهی یک مربع ۲۰۰ در ۲۰۰ از شکل را خروجی دهید که گوشهی بالا-چپ آن، سطر $r$ام از بالا و ستون $c$ام از چپ شکل است. **در صورتی که زیر سطر $r$ام و سمت راست ستون $c$ام شکل یک مربع ۲۰۰ در ۲۰۰ از هر طرفی جا نمیشد، کافیست تا انتهای آن سمت از شکل را چاپ کنید.**
**توضیحات دقیقتر مربوط به اشکال بحثهای سطح بالا:**
طبق تعریف گفته شده، میتوانید فرض کنید که هر شکل بحث از بزرگنمایی شکل بحث سطح پایینتر بوجود میآید که پس از آن داخل تبلت این شکل، شکل بحث ۰ را قرار دادهایم.
در این بزرگنمایی، خطوط صرفاً درازتر میشوند و قطور تر نمیشوند! همچنین بزرگنمایی همیشه با ضریبی طبیعی انجام میشود؛ یعنی طول همهی خطوط در کوچکترین اندازهای طبیعی ضرب میشود که در داخل تبلتها، شکل مورد نظر جا بشود. اگر شکل تبلت را پر نمیکرد، سطرهای پایینی و ستونهای راستی تبلتها خالی میمانند. (این جهتها هنگامیست که از بالا نگاه میکنیم و جهت واقعی تبلتها تاثیری بر اینها ندارد.) چون خطوط بزرگنمایی میشوند، فضاهای خالی بین خطوط نیز قاعدتاً بزرگتر میشوند. **به جزییات شِمای سطح ۱ بسیار دقت کنید!**
اگر دقت کنید، شکل ما متشکل از تعدادی خط افقی و عمودی است. یکی از پیچیدگیهای این بزرگنمایی، بزرگنمایی یک شکل پیوسته در فضای گسستهی جدول است. خانهی در سطر $r$ و ستون $c$ جدول را $(r, c)$ مینامیم. فرض کنید خطی افقی از خانهی $(r, c)$ شروع بشود و در خانهی $(r, c')$ تمام بشود؛ پس طول خط برابر $c' - c$ میشود. (خطوط در شکل واقعی پیوسته هستند؛ پس با اینکه با دید جدولی باید طول این خط برابر $c'-c+1$ باشد اما در دید پیوسته، طول آن برابر $c'-c'$ است.) فرض کنید که بزرگنمایی با ضریب طبیعی $n$ انجام میشود. پس از این بزرگنمایی، طول این خط باید برابر $n(c' - c)$ بشود. پس از آن، دقت کنید که ابعاد تبلت با ضریب بزرگنمایی بزرگ میشود ولی شکل بحث سطح ۰ باید کاملاً در تبلت جا بشود؛ یعنی داخل تبلت باید به اندازهی جدول شکل بحث سطح ۰ فضای خالی وجود داشته باشد.
برای مثال:
+ صندلیهای شِمای بحث سطح ۰، مربعهای بطول ضلع ۳ هستند و صندلیهای شِمای بحث سطح ۱، مربعهایی بطول ضلع ۱۸ هستند.
+ تبلتهای رومیزی شِمای بحث سطح ۰، مربعهای بطول ضلع ۵ هستند.
به این موضوع هم توجه داشته باشید که برای ساخت شکل سطح $n$، باید شکل سطح $n-1$ را طوری بزرگنمایی کنید که شکل سطح ۰ در کوچکترین تبلتهای آن جا بشود؛ نه اینکه شکل سطح ۰ را بزرگنمایی کنید تا شکل سطح $n-1$ در تبلتها جا بشود!
**در این سوال، بسته به تعداد تستهایی که درست پاسخ دهید نمره میگیرید. برنامهی شما هرچه بهینهتر باشد و برای حالات بیشتری پاسخ درست بدهد، نمرهی بیشتری دریافت خواهد کرد.**
# ورودی
ورودی تنها شامل یک خط است که در آن سه عدد $n$ و $x$ و $y$ آمده اند.
$$0 \le n \le 5$$
$$1 \le x, y \le f(n)$$
که $f(n)$ طول ضلع مربع شکل از بالای بحث سطح $n$ است.
**در نصف تستها داریم:** $n \le 3$. **یعنی با این فرض شما حداقل نصف نمره را دریافت میکنید.**
# خروجی
شکل از بالای بخش گفته شده از بحث سطح $n$ را چاپ کنید. **دقت کنید که تمام فواصل باید با space گذاشته شوند. هرگونه کاراکتر اضافی از قبیل space و tab و یا سطر خالی اضافه در داخل شکل باعث غلط محسوب شدن پاسخ شما میشود. space اضافی در انتهای خط و سطرهای خالی از کاراکتر خوانا در انتهای خروجی تاثیری ندارد. (خطوط خالی ابتدا و میانهی خروجی مهم هستند.)**
# مثال
## ورودی نمونه ۱
```
0 1 1
```
## خروجی نمونه ۱
```
----
| |
| |
----
--------------------
| | __ | |
| |/__\| |
| | || | |
| | || | |
| ------ |
| |
------ ------
----| __ | | __ |----
| ||/__\| |/__\|| |
| || || | | || || |
----| || | | || |----
------ ------
| |
| ------ |
| | __ | |
| |/__\| |
| | || | |
| | || | |
--------------------
----
| |
| |
----
```
## ورودی نمونه ۲
```
0 3 9
```
## خروجی نمونه ۲
```
| |
----
----------------
| __ | |
|/__\| |
| || | |
| || | |
------ |
|
-- ------
| | __ |----
\| |/__\|| |
| | || || |
| | || |----
-- ------
|
------ |
| __ | |
|/__\| |
| || | |
| || | |
----------------
----
| |
| |
----
```
## ورودی نمونه ۳
```
1 80 100
```
## خروجی نمونه ۳
```
|----| __ | | __ |---- | | |
|| ||/__\| |/__\|| | | | |
|| || || | | || || | | | |
|----| || | | || |---- | | |
| ------ ------ | | |
| | | | | |
| | ------ | | | |
| | | __ | | | | |
| | |/__\| | | | |
| | | || | | | | |
| | | || | | | | |
| -------------------- | -------------------
| ---- |
| | | |
| | | |
| ---- |
| |
-------------------------------
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
----------------------------------------
```
## ورودی نمونه ۴
```
2 100 300
```
## خروجی نمونه ۴
خروجی نمونه را میتوانید در [اینجا](http://bayanbox.ir/view/3943239977676654844/oup3.txt) ببینید!
بحثهای سطح بالا
+ محدودیت زمان: ۳ ثانیه
+ محدودیت حافظه: ۵۱۲ مگابایت
----------
در جایجای جهان افرادی پیدا میشوند که مسابقهی برنامهنویسی برگزار میکنندِ. از بین این افراد، تعدادی هم هستند که خیلی مسابقهی برنامهنویسی برگزار میکنند! چنین افرادی بسیار نایاب هستند، اما اگر بتوانید با بیش از یکی از ایشان صحبت کنید، میبینید که ویژگیهای مشترک بسیاری دارند!
این مسابقه نیز توسط تعدادی از این افراد طراحی شده. از ویژگیهایی که این افراد دارند، این است که معمولاً برای سوال سخت مسابقه، سوالهای مبحث "شار بیشینه" (یا "فلو") را میپسندند و بسیار از این تیپ سوالها استفاده میکنند! اما این مسابقه یک مسابقهی معمولی نیست؛ از این جهت برگزارکنندگان دوست داشتند این مسابقه تا جای ممکن متفاوت باشد؛ به همین دلیل سوال آخر مسابقه دیگر مربوط به فلو نیست؛ بلکه مربوط به فلوچارت است! (آری! سطح خلاقیت برگزارکنندگان حقیقتاً ستودنیست.)
روندنما(یا flowchart) یکی از ابتداییترین ابزارهاییست که برای نمایش الگوریتمها و برنامهها بکار میرود. روندنما مانند یک زبان برنامهنویسی است که بصورت تصویری و ساده، برنامه را توصیف میکند. یک نمونه از روندنما را میتوانید در شکل زیر ببینید:
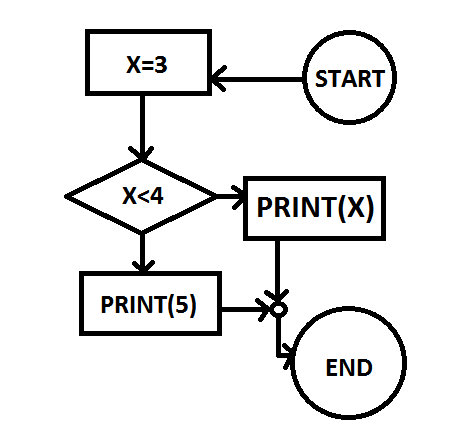
این روندنما در انتها، مقدار ۵ را چاپ میکند.
در این سوال نمونههای سادهای از روندنما مورد بررسی است. فرض کنید در روندنما، چنین ابزارهایی داشته باشیم:
+ **دایرههای شروع و پایان:** در داخل دایرهی شروع `START` و در داخل دایرهی پایان، `END` نوشته شده است. هر روندنما شامل دقیقاً یک دایرهی شروع و یک دایرهی پایان است. دایرهی شروع یک مسیر خروجی دارد و دایرهی پایان یک مسیر ورودی.
+ **دستورها:** دستورها در داخل مستطیل نوشته میشوند. هر مستطیل دستور دقیقاً یک مسیر ورودی دارد و یک مسیر خروجی.
+ **شرطها:** در داخل لوزی، شرط مربوطه میآید. لوزی شرط، یک مسیر ورودی دارد و دو مسیر خروجی که همهی مسیرها از گوشههای لوزی به آن وصل میشوند و همیشه دو مسیر خروجی از گوشههای پایین و راست آن خارج میشوند. در صورت برقرار بودن شرط، برنامه از سمت پایین لوزی ادامه مییابد و در صورت برقرار نبودن شرط، از سمت راست لوزی ادامه مییابد.
+ **تبدیل چند به یک:** در دایرههای کوچک، چند مسیر عبوری وارد میشوند و تنها یک مسیر خروجی خارج میشود. این مسیر خروجی ادغام این چند ورودی است؛ یعنی مسیر برنامه از هریک از ورودیها وارد شد از این خروجی ادامه مییابد.
+ **مسیرهای برنامه:** هر مسیر بصورت یک خط (صاف یا شکسته) که در هر نقطهای یا کاملاً عمودی است و یا کاملاً افقی، از بخشی به بخش دیگر کشیده میشود. انتهای مسیر با یک فلش مشخص میشود. مسیرها میتوانند در وسط تصویر با هم تلاقی داشته باشند؛ اما هر تلاقی دقیقاً شامل یک مسیر افقی و یک مسیر عمودی میشود و فرض میشود که مسیرها در نقاط تلاقی شکستگی ندارند و جهت خود را حفظ میکنند. ممکن است یک مسیر به تعداد دلخواه تلاقی و شکستگی داشته باشد و به هر نقطهی دلخواهی از مستطیل دستور و یا دایرهی شروع یا پایان متصل باشد؛ اما همیشه تقریباً در نقطهی اتصال (در شکلهای نامبرده، بجز شرطها) عمود است.
تنها متغیری که در برنامه استفاده میشود، `X` است که نیازی به تعریف ندارد و ابتدای برنامه مقدارش برابر ۰ است. دستورهایی که ممکن است در برنامه بیایند عبارتند از:
+ به شکل $X=n$ که $n$ یک عدد است و $0 \le n \le 9$؛ یعنی مقدار متغیر $X$ را برابر $n$ قرار بده.
+ به شکل $X++$ که یعنی مقدار $X$ را یک واحد افزایش بده.
+ به شکل $X--$ که یعنی مقدار $X$ را یک واحد کاهش بده.
+ به شکل $PRINT(X)$ که یعنی مقدار متغیر $X$ را در خروجی بنویس در خروجی به سطر جدید برو.
+ به شکل $PRINT(n)$ که $n$ یک عدد است و $0 \le n \le 9$؛ یعنی عدد $n$ را در خروجی بنویس و در خروجی به سطر جدید برو.
همچنین شرطهای ممکن عبارتند از:
+ شرط $X<n$ که $n$ یک عدد است و $0 \le n \le 9$؛ یعنی آیا مقدار $X$ کمتر از $n$ است؟
+ شرط $X>n$ که $n$ یک عدد است و $0 \le n \le 9$؛ یعنی آیا مقدار $X$ بیشتر از $n$ است؟
+ شرط $X=n$ که $n$ یک عدد است و $0 \le n \le 9$؛ یعنی آیا مقدار $X$ برابر $n$ است؟
همچنین فرض کنید که روندنماهای این مسئله، در دور بینهایت نمیافتند و هریک از دستورها حداکثر ۲۰ بار اجرا میشوند.
یک انسان بسادگی میتواند با دیدن چنین روندنمایی، خروجی متناظرش را بدست آورد. حال، آیا شما میتوانید برنامهای بنویسید که چنین کند؟!
برای سادهتر شدن کار، روندنما بصورت تصویر به شما داده نمیشود؛ بلکه بصورت تعدادی رشته داده میشود. روندنماهای این مسئله با دست کشیده شدهاند (مانند مثال بالا). ابتدا شکل آن کشیده شده و تبدیل به تعدادی رشته متشکل از کاراکترهای `.` و `#` شده که `.` نمایانگر رنگ سفید و `#` نمایانگر رنگ سیاه است. سپس دستورات و نوشتهها در داخل رشتهها بصورتی که واقعاً نوشته میشوند، اضافه میشوند و ابعاد جدول نیز به در ابتدای ورودی میآید.
**در این سوال، بسته به تعداد تستهایی که درست پاسخ دهید نمره میگیرید. برنامهی شما هرچه بهینهتر باشد و برای حالات بیشتری پاسخ درست بدهد، نمرهی بیشتری دریافت خواهد کرد.**
# ورودی
ورودی برنامهی شما، یک روندنما به شکل گفتهشده است. جدول آن حداکثر ۵۰۰ سطر و حداکثر ۷۰۰ ستون دارد. شکل روندنما برای انسان کاملاً قابل فهم خواهد بود.
# خروجی
به ازای هر دستور `PRINT` که در روندنما اجرا میشود، مقدار مربوطه را در یک سطر جدا چاپ دهید.
# مثال
## ورودی نمونه ۱
ورودی برای شکل داخل صورت سوال در [این فایل](http://bayanbox.ir/view/2602472539016892301/test.txt) آمده است.
## خروجی نمونه ۱
```
5
```
## ورودی نمونه ۲
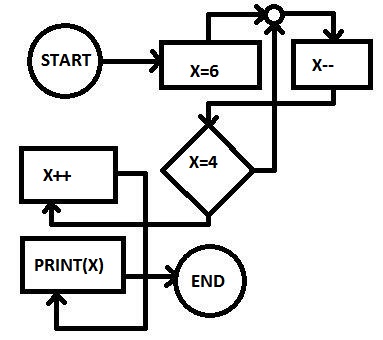
ورودی برای شکل زیر در [این فایل](http://bayanbox.ir/view/7394482655309972351/test2-in.txt) آمده است.
## خروجی نمونه ۲
```
5
```