• محدودیت زمان: ۰.۵ ثانیه
• محدودیت حافظه: ۶۴ مگابایت

یک موش در خانه عمو اسکروچ وجود دارد! عمو اسکروچ می‌خواهد این موش به سوراخ موش برود و سپس در سوراخ را مسدود کند. او معتقد است اگر این موش به سوراخ خودش نرود، سال ۱۳۹۹ که سال موش است تحویل نخواهد شد!

موش و سوراخ موش روی محور افقی سه‌تایی که از صفر تا دو شماره‌گذاری شده قرار دارند (سمت چپ‌ترین نقطه ۰ و سمت راست‌ترین نقطه ۲ است). موش در نقطه $x_1$ و سوراخ موش در نقطه $x_2$ قرار دارد. توجه کنید ممکن است محل اولیه موش و سوراخ موش یکسان باشد.

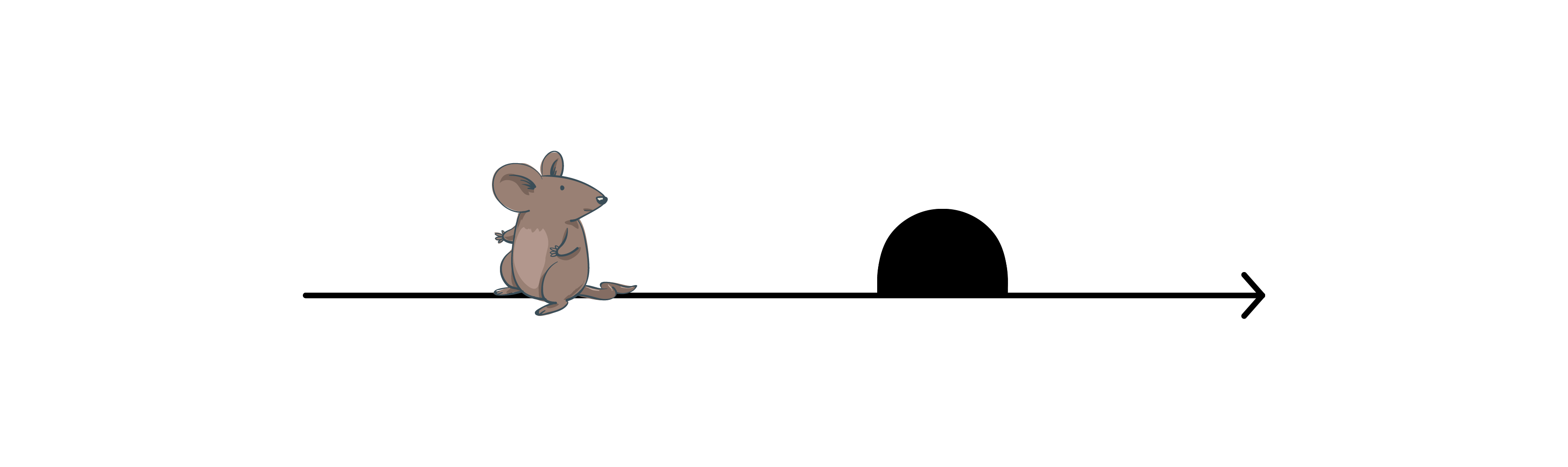
موش در هر حرکت یک واحد به سمت چپ یا یک واحد به سمت راست می‌رود. عمو اسکروچ که دل خوشی از سال ۱۳۹۹ ندارد، می‌خواهد موش با کمترین تعداد حرکت به سوراخش برسد تا سال سریع‌تر تحویل شود.

او از شما می‌خواهد طوری حرکت‌های موش را مشخص کنید که با کمترین تعداد حرکت به سوراخش برسد.

ورودی🔗

ورودی تنها شامل یک خط است که در آن دو عدد صحیح $x_1$ و $x_2$ با فاصله از هم که به ترتیب نشان دهنده محل اولیه موش و محل سوراخ موش روی محور افقی آمده است. $0 \le x_1, x_2 \le 2$

خروجی🔗

حرکت‌های موش از محل اولیه تا سوراخ موش را به صورت یک رشته از L و R چاپ کنید که این دو کاراکتر به ترتیب نشان دهنده حرکت موش به چپ و راست است.

اگر مکان اولیه موش و سوراخ موش یکسان بود تنها عبارت Saal Noo Mobarak! را چاپ کنید.

اگر چند مسیر با تعداد حرکت کمینه وجود دارد یک مسیر را به دلخواه چاپ کنید.

مثال🔗

ورودی نمونه ۱🔗

0 2

خروجی نمونه ۱🔗

RR

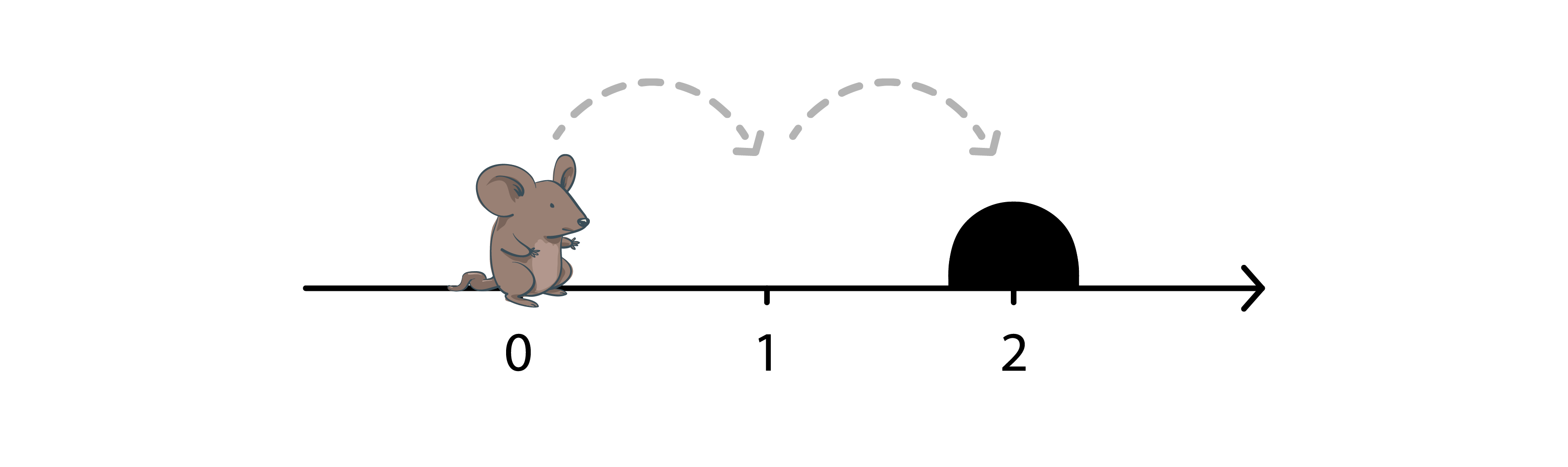
ورودی نمونه ۲🔗

1 1

خروجی نمونه ۲🔗

Saal Noo Mobarak!

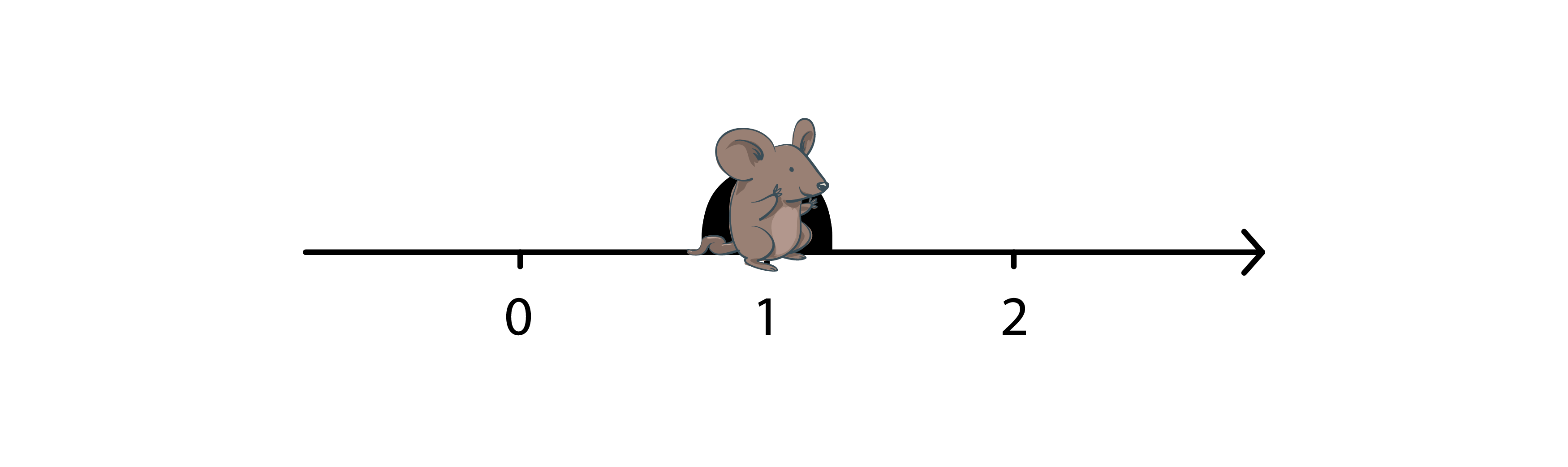
ورودی نمونه ۳🔗

1 0

خروجی نمونه ۳🔗

L

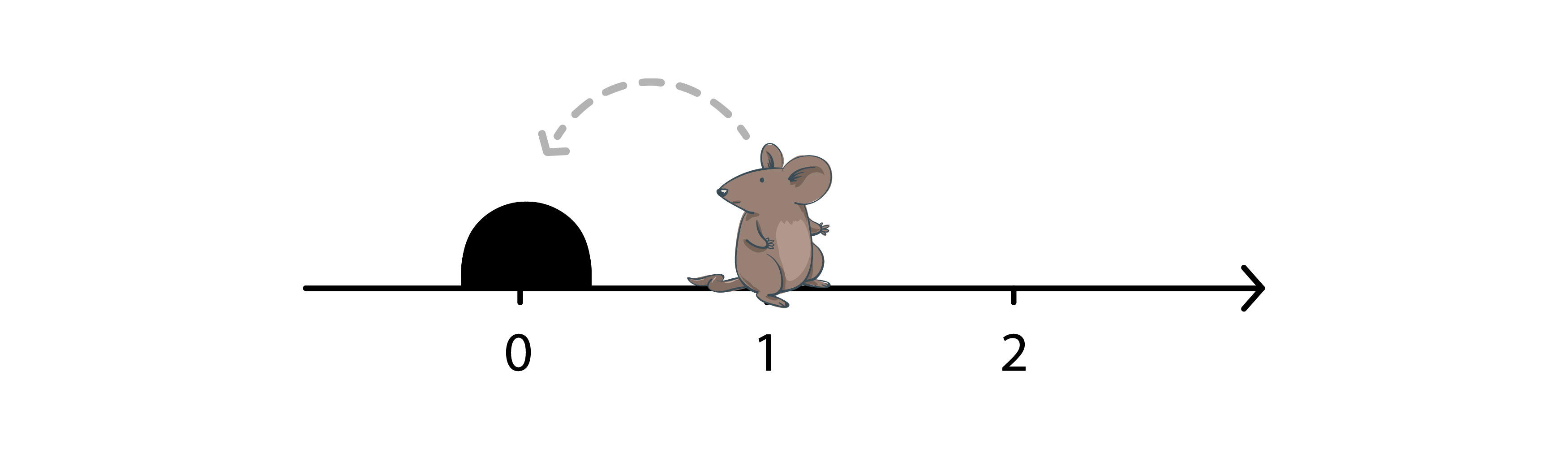
• محدودیت زمان: ۰.۵ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

عمو اسکروچ تصمیم گرفته در پایان سال یک شماره تلفن رند سفارش بدهد. شماره عمو اسکروچ باید ۸ رقمی باشد و با صفر شروع نشود (برای مثال شماره تلفن 01234567 معتبر نیست).

عمو اسکروچ معتقد است یک شماره تلفن رند است اگر حداقل یکی از شرایط زیر را داشته باشد:

۱. رقمی موجود باشد که حداقل ۴ بار در آن تکرار شده باشد.

برای مثال شماره‌های 73433323 و 12131415 هر دو این ویژگی را دارند زیرا در شماره‌ی اول رقم ۳، ۵ بار و در شماره‌ی دوم رقم ۱، ۴ بار تکرار شده ولی شماره‌های 12435127 و 70215498 این ویژگی را ندارند (چون هر یک از ارقام 0 تا 9 حداکثر دو بار در این شماره تکرار شده است).

۲. سه رقم متوالی در این شماره برابر باشند.

مثلاً شماره‌‌های 85711124 و 77777521 این ویژگی را دارند زیرا در شماره اول ۳ رقم ۱ متوالی و در شماره دوم ۴ رقم ۷ متوالی وجود دارد؛ ولی شماره‌های 11223344 و 12121212 این ویژگی را ندارند چون هیچ سه رقم متوالی آنها یکسان نیستند.

۳. شماره آینه‌ای باشد. یعنی اگر شماره را از راست بنویسیم برابر با خودش شود.

مثلاً شماره‌های 12344321 و 17288271 این ویژگی را دارند ولی دو شماره‌های 17569823 و 12344320 این ویژگی را ندارند.

عمو اسکروچ در حال انتخاب شماره‌ی رند و از از شما می‌خواهد که به او کمک کنید تا شماره‌های رند را تشخیص دهد. برای همین به شما $t$ شماره تلفن می‌دهد و از شما می‌خواهد بررسی کنید که کدام یک از این $t$ شماره تلفن، رند هستند.

ورودی🔗

در سطر اول ورودی یک عدد طبیعی $t$ آمده که نشان‌دهنده تعداد شماره‌هایی است که شما باید بررسی کنید. در هر یک از $t$ سطر بعدی یک رشته ۸ رقمی که نشان‌دهنده یک شماره تلفن است به شما داده می‌شود. $1 \le t \le 1\ 000$

تضمین می‌شود شماره‌های تلفن با رقم 0 آغاز نمی‌شود.

خروجی🔗

خروجی شامل $t$ سطر است. اگر شماره‌ی $k$ اًم داده شده در ورودی رند باشد در سطر $k$ اًم خروجی عبارت Ronde! و در غیر این صورت عبارت Rond Nist را چاپ کنید.

مثال🔗

ورودی نمونه ۱🔗

5
11111111
12345678
34666825
12344321
17544721

خروجی نمونه ۱🔗

Ronde!
Rond Nist
Ronde!
Ronde!
Rond Nist

شماره‌ی 11111111 رند است زیرا هر سه ویژگی را دارد.
شماره‌ی 12345678 رند نیست زیرا هیچ کدام از سه ویژگی گفته شده را ندارد.
شماره‌ی 34666825 رند است زیرا ویژگی دوم را دارد یعنی سه رقم متوالی ۶ را دارد.
شماره‌ی 12344321 رند است زیرا ویژگی سوم را دارد یعنی آینه‌ای است و اگر آن را از راست بخوانیم، با خود آن شماره برابر می‌شود.
شماره‌ی 17544721 رند نیست چون هیچ کدام از سه ویژگی گفته شده را ندارد.

• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

عمو اسکروچ که دلش حسابی برای اعضای خاندانش تنگ شده، تصمیم دارد در جشن سال نوی آن‌ها (به صورت آنلاین!) شرکت کند. خاندان عمو اسکروچ $n-1$ نفره است و هر یک از آن‌ها یک جشن برگزار می‌کند. عمو اسکروچ که نمی‌تواند با یک موبایل در دو جشن شرکت کند نیاز به $n-1$ موبایل با شارژ کامل دارد. او برای تامین این تعداد موبایل پیش دوستش رفته است.

دوست عمو اسکروچ $n$ موبایل دارد و موبایل $i$ اُم $a_i$ درصد شارژ دارد. شارژر اسرارآمیزی هم داریم که می‌توان با آن از موبایلی که حداقل $x$ درصد شارژ دارد، $x$ درصد شارژ کم کرد و به موبایلی دیگر $y$ درصد شارژ اضافه کرد. از آنجایی که طبق گفته‌ی فیزیک‌دانان پایستگی انرژی برقرار است، مقدار $x$ حتماً از مقدار $y$ بیشتر است.

از آن جا که عمو اسکروچ وقت زیادی برای پر کردن شارژ موبایل‌ها ندارد، می‌خواهد بداند که آیا می‌تواند با استفاده از شارژر اسرارآمیز $n-1$ موبایل را به طور کامل شارژ کند؟ عمو اسکروچ که درگیر کارهای سال نوست و وقت ندارد از شما می‌خواهد که به او کمک کنید.

دقت کنید که اگر طی عملیاتی، شارژ موبایلی بیش از ۱۰۰ درصد شد، شارژ آن را همان ۱۰۰ درصد در نظر می‌گیریم.

ورودی🔗

ورودی تنها شامل دو خط است که در خط اول به ترتیب $n$، $x$ و $y$ و در خط بعد $n$ عدد آمده است که عدد $i$ اًم برابر با $a_i$ خواهد بود. $2 \le n \le 100$ $1 \le y < x \le 100$ $0 \le a_i \le 100$

خروجی🔗

خروجی شامل یک خط است که پاسخ به مسئله خواهد بود. در صورتی که می‌توان شارژ $n-1$ موبایل را به ۱۰۰ رساند، عبارت YES و در غیر این صورت NO را چاپ کنید.

مثال🔗

ورودی نمونه ۱🔗

2 4 2
9 99

خروجی نمونه ۱🔗

YES

اگر ۴ درصد شارژ از موبایل اول کم کنیم و ۲ درصد شارژ به دومی بدهیم، در نهایت موبایل اول ۵ درصد و موبایل دوم ۱۰۰ درصد شارژ خواهد داشت.

ورودی نمونه ۲🔗

3 3 2
10 95 98

خروجی نمونه ۲🔗

NO

به هیچ طریق نمی‌توان دو موبایل با شارژ ۱۰۰ به دست آورد.

• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

عمو اسکروچ که خبر رسیدن قرن جدید را شنیده بود، بالأخره تصمیم گرفت خانه‌ تکانی کند. در میان تمیزکاری‌‌هایش به پنجره‌ای بسیار کثیف برخورد و فهمید در خانه‌اش هیچ شیشه پاک‌کنی ندارد. پس تصمیم به خرید یک شیشه پاک‌کن گرفت.

شیشه‌ی پنجره‌ی خانه عمو اسکروچ به شکل یک جدول $n \times n$ است که در $k$ خانه‌ی آن، یک لکه وجود دارد. ابتدا شیشه پاک‌کن را به صورت افقی در مکانی دلخواه روی ردیف اول شیشه قرار می‌دهیم و سپس در هر مرحله شیشه پاک‌کن را از روی پنجره بلند کرده، آن را یک ردیف پایین آورده، در راستای افقی حداکثر یک واحد جا‌به‌جا کرده و دوباره روی شیشه می‌گذاریم (شیشه‌ پاک‌کن نباید از شیشه بیرون بزند)، در این صورت تمام خانه‌های شیشه که زیر شیشه پاک‌کن هستند تمیز می‌شوند.

از آنجایی که عمو اسکروچ نمی‌خواهد هزینه‌ی زیادی کند، به دنبال کوتاه‌ترین شیشه پاک‌کنی می‌گردد که بتواند تمام $k$ لکه را پاک کند. به او در پیدا کردن طول این شیشه پاک‌کن کمک کنید.

ورودی🔗

در خط اول ورودی دو عدد $n$ و $k$ آمده که به ترتیب نشان دهنده‌ی طول ضلع پنجره و تعداد لکه‌های روی آن است.

در خط $i$ ام از $k$ خط بعدی دو عدد $x_i$ و $y_i$ آمده که به ترتیب نشانگر شماره ردیف و ستون لکه‌ی $i$ اُم است. $2 \le n \le 100\ 000$ $1 \le k\,\leq\,\min\left(300\,000,\,n\times n\right)$ $1 \le x_i, y_i \le n$

تضمین می‌شود در هیچ خانه‌ای بیش از یک لکه وجود ندارد.

خروجی🔗

در تنها خط خروجی کمترین طول شیشه پاک‌کن را چاپ کنید.

مثال🔗

ورودی نمونه ۱🔗

5 6
1 1
1 3
2 2
2 4
3 5
4 5

خروجی نمونه ۱🔗

3

با شیشه پاک‌کن به طول کمتر از ۳ نمی‌توان لکه‌ها را پاک کرد. اما با استفاده از شیشه پاک‌کن به طول ۳، می‌توان به صورت زیر شیشه را پاک کرد:

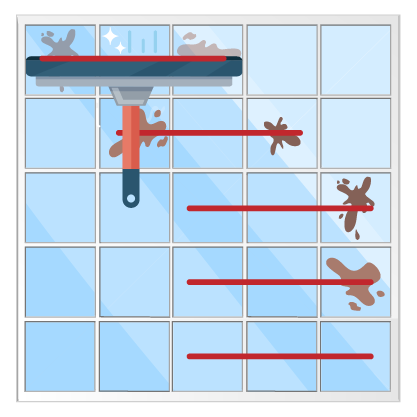
ورودی نمونه ۲🔗

4 7
1 1
1 2
2 2
2 4
3 3
4 1
4 2

خروجی نمونه ۲🔗

3

با شیشه پاک‌کن به طول کمتر از ۳ نمی‌توان لکه‌ها را پاک کرد. اما با استفاده از شیشه پاک‌کن به طول ۳، می‌توان به صورت زیر شیشه را پاک کرد:

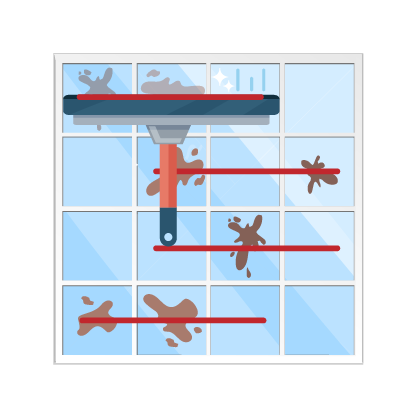
• محدودیت زمان: ۳ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

عمو اسکروچ پس از خانه تکانی برای پذیرایی از خود و جبران انرژی از دست‌رفته تصمیم به تدارک غذایی لذیذ برای شب سال نو گرفت. برای همین کتاب آشپزی خود را باز کرد. اما پس از دیدن مواد اولیه‌ی غذاها گیج شد زیرا هیچ‌کدام از آن‌ها را نمی‌شناخت. در نتیجه شروع به جست‌وجوی ‌آن‌ها در اینترنت کرد.

نام کل مواد اولیه موجود در کتاب به صورت $n$ رشته‌ی $s_{1}\,,\,s_{2}\,,\,...\,,\,s_{n}\$ است. عمو اسکروچ برای پخت غذای لذیذ خود، در $q$ مرحله مجموعه‌ی مواد اولیه‌ی انتخابی خود را به صورت زیر تغییر می‌دهد (در ابتدا لیست مواد اولیه‌ی انتخابی خالی است):

• عدد $i$ ($1 \le i \le n$) را انتخاب می‌کند اگر $s_i$ در مجموعه‌اش بود آن را حذف و در غیر این صورت آن را اضافه می‌کند.

دکمه‌های روی کیبورد عمو اسکروچ شامل حروف کوچک انگلیسی و کلیدهای $Backspace$ و $Enter$ است. برای فشردن هر دکمه به غیر از دکمه‌ی $Enter$، یک واحد انرژی مصرف می‌شود (فشردن دکمه‌ی $Enter$ به دلیل لذت‌بخش بودن، انرژی‌ای لازم ندارد).

روند جست‌وجو به این صورت است که عمو اسکروچ ترتیبی دلخواه از مواد اولیه مجموعه‌اش انتخاب کرده و هر کدام را دقیقاً یک بار جست‌وجو می‌کند، برای جست‌وجوی یک رشته باید ابتدا آن رشته را بنویسد و سپس کلید $Enter$ را فشار دهد (برای جزئیات بیشتر توضیح مثال را مشاهده کنید).

از آنجا که عمو اسکروچ انرژی زیادی ندارد، از شما می‌خواهد که به او بگویید پس از هر مرحله تغییر، به ازای تمام حالات تایپ کردن مواد اولیه‌ی لیست دلخواه خود، کمترین میزان انرژی‌ای که صرف می‌کند چقدر است.

ورودی🔗

در خط اول دو عدد $n$ و $q$ آمده که نشان دهنده‌ی تعداد مواد اولیه و تعداد تغییرات است.

سپس در خط $i$ اًم از $n$ خط بعدی رشته‌ی $s_i$ از حروف کوچک انگلیسی آمده است.

در خط $i$ اًم از $q$ خط بعدی نیز عدد $x_i$ آمده که عدد انتخاب شده توسط عمو اسکروچ را نشان می‌دهد. $1 \le n \le 100\ 000$ $1 \le q \le 200\ 000$ $1 \le x_i \le n$

تضمین می‌شود جمع طول رشته‌ها از $100\ 000$ کمتر است همچنین رشته‌های ورودی متمایزند.

خروجی🔗

در خروجی $q$ خط چاپ کنید، به طوری که در خط $i$ اًم، پاسخ مسئله بعد از تغییر $i$ اًم باشد.

مثال🔗

ورودی نمونه ۱🔗

3 5
aab
ab
abc
1
2
3
2
3

خروجی نمونه ۱🔗

3
5
7
7
3

تغییر اول: مجموعه به ${aab}$ تبدیل می‌شود که برای جست‌وجوی آن به ترتیب کلیدهای زیر را فشار می‌دهیم (توجه کنید که کلید $Enter$ انرژی‌ای کم نمی‌کند):

$a, a, b, Enter$

تغییر دوم: مجموعه به ${aab,ab}$ تبدیل می‌شود که برای جست‌وجوی آن به ترتیب کلیدهای زیر را فشار می‌دهیم:

$a, b, Enter, Backspace, a, b, Enter$

تغییر سوم: مجموعه به ${aab,ab,abc}$ تبدیل می‌شود که برای جست‌وجوی آن به ترتیب کلیدهای زیر را فشار می‌دهیم:

$a, a, b, Enter, Backspace, Backspace, b, Enter, c, Enter$

تغییر چهارم: مجموعه به ${aab,abc}$ تبدیل می‌شود که برای جست‌وجوی آن به ترتیب کلیدهای زیر را فشار می‌دهیم:

$a, a, b, Enter, Backspace, Backspace, b, c, Enter$

ورودی نمونه ۲🔗

4 7
aca
abb
baa
bab
4
3
1
2
2
4
1

خروجی نمونه ۲🔗

3
5
11
15
11
9
3

• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

عمو اسکروچ که آدم سنگینی است، برای اینکه سنگینی خودش را به دوستان خود اثبات کند، تصمیم گرفت که یک مسئله‌ی گراف را برای آنها حل کند. ولی از آنجا که او علاوه بر سنگین بودن، حق‌گویی پایینی دارد از شما کمک می‌خواهد تا مسئله را برای او حل کنید:

یک گراف ساده‌ی $n$ رأسی داریم. سنگینی یک مسیر را برابر با XOR اعداد روی یال‌های آن در نظر می‌گیریم. تابع $f$ را برای دو رأس $v$ و $u$ برابر با بیشترین مقدار سنگینی بین تمام مسیرهای ساده بین دو رأس $v$ و $u$ قرار می‌دهیم (در صورتی که بین این دو رأس مسیری نباشد، برابر با صفر قرار می‌دهیم). می‌خواهیم روی یال‌های گراف اعداد ۰ یا ۱ بنویسیم به طوری مقدار زیر بیشینه شود: $\sum_{v < u \in V \left (G \right)}f\left(v, u\right)$ بیشینه مقدار این عبارت را خروجی دهید.

ورودی🔗

در خط اول ورودی، دو عدد طبیعی $n$ و $m$ با فاصله از هم آمده است که به ترتیب نشان دهنده‌ی تعداد رئوس و یال‌های گراف است. در ادامه، $m$ خط آمده است و در خط $i$ اًم، دو عدد $v_i$ و $u_i$ آمده است که نشان دهنده‌ی یک یال، بین این دو رأس است. $3 \le n \le 100\ 000$ $1 \le m \le 200\ 000$$1 \le v_i, u_i \le n$

خروجی🔗

در تنها خط خروجی، جواب مسئله را چاپ کنید.

مثال🔗

ورودی نمونه ۱🔗

4 4
1 2
2 3
3 4
4 1

خروجی نمونه ۱🔗

6

اگر روی یال (2, 1) عدد ۱، و روی باقی یال‌ها عدد ۰ بنویسیم، گرافی به شکل زیر خواهیم داشت:

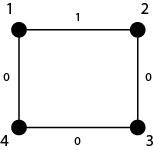
در این صورت مقادیر مختلف $f$ به شکل زیر خواهد بود:
مقدار تابع به ازای رأس‌های ۱ و ۲ برابر ۱ خواهد بود، زیرا می‌توان مسیر $1\to2$ را انتخاب کرد.
مقدار تابع به ازای رأس‌های ۱ و ۳ برابر ۱ خواهد بود، زیرا می‌توان مسیر $1\to2\to3$ را انتخاب کرد.
مقدار تابع به ازای رأس‌های ۱ و ۴ برابر ۱ خواهد بود، زیرا می‌توان مسیر $1\to2\to3\to4$ را انتخاب کرد.
مقدار تابع به ازای رأس‌های ۲ و ۳ برابر ۱ خواهد بود، زیرا می‌توان مسیر $2\to1\to4\to3$ را انتخاب کرد.
مقدار تابع به ازای رأس‌های ۲ و ۴ برابر ۱ خواهد بود، زیرا می‌توان مسیر $2\to1\to4$ را انتخاب کرد.
مقدار تابع به ازای رأس‌های ۳ و ۴ برابر ۱ خواهد بود، زیرا می‌توان مسیر $3\to2\to1\to4$ را انتخاب کرد.

ورودی نمونه ۲🔗

5 4
1 2
2 3
3 1
4 5

خروجی نمونه ۲🔗

4

• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

یک بار دیگر سال جدید رسید و همه شاد بودند؛ همه به جز عمو اسکروچ!

یکی از مهم‌ترین و کهن‌ترین رسم‌ها در هنگام عید، عیدی دادن است و عمو اسکروچ از این رسم به شدت بیزار است؛ اما مجبور است به دلیل حفظ آبرو پیش در و همسایه‌ها به برادرزاده‌ها و خواهرزاده‌هایش عیدی بدهد. مراحل عیدی دادن کمی عجیب است. آن را مرحله به مرحله برای شما شرح می‌دهیم.

1. شب قبل از عید، برادرزاده‌ها و خواهرزاده‌ها همگی در یک مکان جمع می‌شوند و مشخص می‌کنند در مجموع چقدر عمو اسکروچ را تیغ می‌زنند؛ سپس به عمو‌ اسکروچ ایمیل می‌زنند و به او می‌گویند که جمعاً از او $S$ اسکروچی (یک اسکروچی معادل با یک میلیاردم بیت کوین است) به عنوان عیدی می‌خواهند.

2. عمو اسکروچ ایمیل را می‌بیند و از ترس به خود می‌لرزد. سپس با مشاورش صحبت می‌کند و مشاورش به او پیشنهاد می‌دهد که $k$ اسکناس به ارزش $a_1, ..., a_k$ در کیف پولش بگذارد. از آن‌جایی که مشاور مرد بسیار دقیقی است دنباله را چنان انتخاب می‌کند که $\sum a_i = S$ باشد.

3. در روز عید تمام $n$ برادرزاده و خواهرزاده به صورت ناگهانی به خانه عمو اسکروچ هجوم می‌آورند و $i$ امین آن‌ها طلب $p_i$ اسکروچی می‌کند. سپس عمو کیف پولش را باز می‌کند (که در آن $k$ اسکناس است) و به هر کدام از آن‌ها تعدادی اسکناس می‌دهد، به طوریکه در نهایت هر کس دقیقا به همان‌اندازه‌ای که طلب کرده بود، اسکروچی بگیرد. سپس برادرزاده‌ها و خواهر‌زاده‌ها به صورت مسالمت‌آمیز خانه عمو اسکروچ را ترک می‌کنند و تا یک سال دیگر بر نمی‌گردند (که ایده‌‌آل ترین حالت برای عمو اسکروچ است). اما ممکن است در این میان مشاور عمو اشتباه محاسباتی کرده باشد و عمو نتواند اسکناس‌ها را بین بچه‌ها تقسیم کند. در این حالت بچه‌ها داد و هوار راه می‌اندازند و عمو پیش در و همسایه‌ها شرمنده می‌شود. توجه کنید مشاور هنگام انتخاب اسکناس‌ها مقدار $p_i$ ها را نمی‌داند.

مراحلی که در بالا گفته شد هر سال تکرار می‌شود. یکی از دغدغه‌های عمو این است که کیف پولش سنگین و بزرگ به نظر نرسد (در اینصورت ممکن است بقیه هم او را تیغ بزنند) برای همین به مشاورش گفته است که اسکناس‌های پیشنهادی را طوری انتخاب کند که تعداد آن‌ها (همان $k$) کمینه باشد.

امسال ش.پ (که یک المپیاد کامپیوتری و از دوستان عمو اسکروچ است) برای او برنامه‌ای نوشته که به کمک آن می‌تواند تشخیص دهد مشاورش چقدر بالیاقت است. برنامه به این‌صورت است که $n$ (تعداد برادرزاده‌ها و خواهرزاده‌های عمو اسکروچ)، $S$ (جمع مقداری که بچه‌ها عیدی طلب می‌کنند) و $a_1, a_2, ..., a_k$ (دنباله اسکناس‌های پیشنهادی مشاور) را تحویل می‌گیرد و یکی از سه رشته زیر را به عنوان گزارش بر می‌گرداند:

• اگر حالتی از طلب کردن عیدی‌ها وجود داشته باشد که عمو نتواند عیدی‌ها را پرداخت کند و در نتیجه پیش در و همسایه‌ها شرمنده شود، برنامه رشته wrong را بر می‌گرداند.

• در غیر این‌صورت اگر حالتی وجود نداشت که عمو شرمنده بشود ولی $k$ کمینه نبود، برنامه رشتهvalid را بر می‌گرداند.

• اگر علاوه بر شرمنده نشدن، $k$ نیز کمینه بود، برنامه optimal را بر می‌گرداند.

از آن‌جایی که ش.پ از مشکل ضعیف بودن رنج می‌برد، برنامه‌ای که نوشته بسیار کند است. عمو اسکروچ به همین منظور بخشی از بیت‌کوین‌هایش را صرف برگزاری این مسابقه کرده و می‌خواهد کسی را پیدا کند که برنامه مشابهی برای او بنویسد تا به وسیله آن مشاورش را در $q$ سال خدمت‌اش ارزیابی کند.

ورودی🔗

در خط اول ورودی عدد $q$ نوشته شده است. که تعداد سال‌های مختلفی است که عمو اسکروچ می‌خواهد مشاورش را محک بزند. سپس داده‌های مربوط به $q$ سال گذشته به صورت زیر به شما ورودی داده می‌شوند.

اعداد $n$ (تعداد بچه‌ها)، $k$ (تعداد اسکناس‌های پیشنهادی مشاور) و $S$ (جمع طلب بچه‌ها) به ترتیب و در یک خط به شما ورودی داده می‌شوند. در خط بعد دنباله $a_1,a_2,...,a_k$ داده می‌شوند که اسکناس‌های پیشنهادی مشاور است.

$1 \leq n \leq 200$ $0 \leq a_i \leq S \leq 10^{18}$ $\sum a_i = S$ $1 \leq k \leq 100\ 000$

تضمین می‌شود که جمع تمام $k$ ها حداکثر $100\ 000$ است.

خروجی🔗

به ازای هر کدام از $q$ پرسش، جواب مسئله که یکی از سه رشته wrong، valid یا optimal است را خروجی دهید.

مثال🔗

ورودی نمونه ۱🔗

3
2 4 10
4 3 2 1 
2 6 10
1 1 1 1 1 5 
2 4 10
1 3 3 3 

خروجی نمونه ۱🔗

optimal
valid
wrong

در پرسش دوم، تعداد اسکناس‌ها بهینه نیست ولی همچنان هرطور که ۲ بچه عیدی بخواهند می‌تواند پاسخ‌گوی نیاز آن‌ها باشد.

در پرسش سوم، اگر بچه اول ۲ اسکروچی و بچه دوم ۸ اسکروچی طلب کند، عمو شرمنده می‌شود.

ورودی نمونه ۲🔗

2
200 6 6
1 1 1 1 1 1 
200 5 6
1 1 2 1 1 

خروجی نمونه ۲🔗

optimal
wrong

در ۲ پرسش این مثال، تعداد بچه‌ها ۲۰۰، و جمع پول درخواستی آن‌ها ۶ است. در نتیجه تعداد زیادی از آن‌ها قرار است ۰ واحد پول در‌خواست کنند. در حالتی که ۶ نفر ۱ اسکروچی بخواهند و بقیه اسکروچی نخواهند، عمو مجبور است ۶ اسکناس با ارزش ۱ داشته باشد.