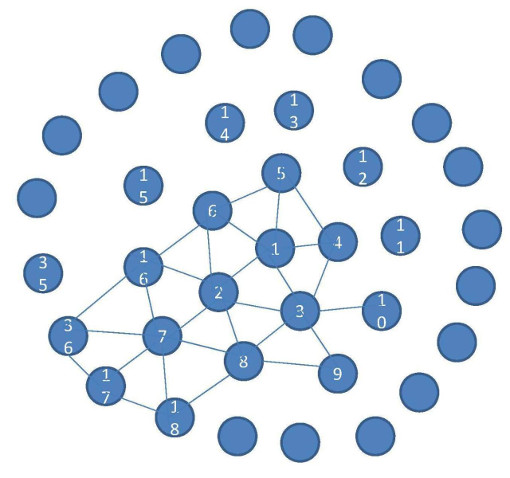
+ محدودیت زمان: ۲ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- زنبورهای شهر عجیب به شکل زیر کندوهایشان را می‌سازند. کندوی ۱ در مرکز قرار دارد و در سطح های بعدی ۵ کندو با شماره‌های ۲ تا ۶ قرار می‌گیرند. در سطح‌های بعدی نیز به ترتیب ۱۰ و ۲۰ و ۴۰ و... کندو قرار خواهند گرفت. هر کندو به کندوهای مجاورش راه دارد. در ورودی اندیس دو کندو می‌آید و شما باید طول کوتاه‌ترین مسیر بین آن دو کندو را بیابید.  # ورودی ورودی تنها شامل یک خط است که در آن دو عدد طبیعی $i$ و $j$ با فاصله از هم آمده است. $$1 \le i, j \le 10^6$$ # خروجی خروجی برنامه‌ی شما باید شامل ۱ عدد صحیح باشد که برابر طول کوتاه‌ترین مسیر بین دو کندوی $i$ و $j$ است. # زیرمسئله‌ها | زیرمسئله | نمره | محدودیت |:------------------:|:----------:|:------------------:| | ۱ | ۱۰۰ | بدون محدودیت اضافی | # مثال ## ورودی نمونه ۱ ``` 5 36 ``` ## خروجی نمونه ۱ ``` 3 ``` ## ورودی نمونه ۲ ``` 4 17 ``` ## خروجی نمونه ۲ ``` 4 ```

+ محدودیت زمان: ۲ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- به شما یک آرایه $A_1, A_2, ..., A_n$ داده شده است. مطلوب است محاسبه‌ی مقدار عبارت زیر به ازای تعدادی دوتایی $s$ و $k$ مختلف. $$\sum _{i = 0} ^{\lfloor \frac{n - s}{k} \rfloor } A_{i \times k + s} = A_{s} + A_{s + k} + A_{s + 2k} + ...$$ # ورودی در سطر اوّل ورودی عدد $n$ می‌آید. در سطر دوم $n$ عدد می‌آید که عدد $i$ام برابر $A_i$ است. در سطر سوم عدد $Q$ به تنهایی می‌آید که برابر تعداد دوتایی‌های $s$ و $k$ است که در ادامه داده خواهند شد. در هر یک از $Q$ سطر بعد دو عدد خواهد آمد. عدد اوّل $s$ و عدد دوم $k$ است. تمام اعداد آرایه، طبیعی و کم‌تر از $10^9$ هستند. $$1 \leq n, Q \leq 100\ 000$$ # خروجی خروجی دارای $Q$ خط است. در $i$امین خط باید مقدار عبارت مذکور را به ازای درخواست $i$ام چاپ کنید. # زیرمسئله‌ها | زیرمسئله | نمره | محدودیت |:------------------:|:----------:|:------------------:| | ۱ | ۱۰۰ | بدون محدودیت اضافی | # مثال ## ورودی نمونه ``` 6 11 3 15 8 5 1 4 1 2 5 1 2 4 3 1 ``` ## خروجی نمونه ``` 31 6 4 29 ```

+ محدودیت زمان: ۲ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- خیکوله بعد از اتمام «Persian Empire» بازی جدیدی به نام «Cheshme Empire» خریده است. این بازی نیز از نوع استراتژیک است. و در ابتدای آن یک نقشه از امپراطوری داده می‌شود که بازی در آن جا انجام می‌شود. این نقشه یک گراف با $n$ راس و $m$ یال است که هر راس معادل یک شهر و هر یال معادل یک جاده است. در اوّلین مرحله‌ی این بازی خیکوله باید برنامه‌ای برای جمع‌آوری محصولات کشاورزی در انبار مرکزی امپراطوری طراحی کند. در این امپراطوری $k$ كشاورز زندگی می‌كند كه كشاورز $i$ام در شهر $v_i$ یك مزرعه دارد. در این مرحله برای نقل و انتقال محصولات كشاورزی باید آن ها را در گونی‌های مخصوصی ریخت و به وسیله‌ی جاده‌ها انتقالشان داد. بنابراین محصولات كشاورز $i$ام در یك گونی به وزن $m_i$ كیلو در شهر $v_i$ قرار دارد. خیكوله باید همه‌ی این محصولات را به انبار مركزی كه در شهر $t$ ساخته شده است انتقال دهد. جاده‌ها دوطرفه هستند و هر جاده یك «هزینه‌ی عبور» و یك «ظرفیت عبور» دارد. وقتی «هزینه‌ی عبور» یك جاده $x$ است یعنی خیكوله به ازای هر گونی كه از این جاده رد می‌كند باید $x$ تومان پرداخت كند. وقتی «ظرفیت عبور» یك جاده $x$ است یعنی تنها گونی‌هایی كه وزنشان از $x$ كیلو بیشتر نیست از این جاده قابلیت عبور دارند. به خاطر محدودیت ظرفیت جاده ها، گاهی نیاز می‌شود تا چند گونی اضافه خریده شود و بخشی از بار یك گونی در گونی‌های جدید ریخته شود. هزینه‌ی خرید هر گونی جدید $c$ تومان است. دقت كنید كه نمی‌توان بار دو گونی مختلف را در یك گونی ریخت و تنها تغییر ممكن در بار گونی‌ها این است كه بخشی از بار یك گونی را در چند گونی جدید خریداری شده، پخش كرد. توجه كنید كه هزینه‌ی عبور هر گونی مستقل از گونی‌های دیگر محاسبه می‌شود. خیكوله بعد از دیدن این همه پیچیدگی از ادامه بازی منصرف شد و رفت تا «Persian Empire II» را بازی كند. حالا نوبت شماست تا برنامه‌ای بنویسید كه: ۱- مشخصات امپراطوری را از ورودی بخواند. ۲- کم‌ترین میزان هزینه برای انتقال همه‌ی محصولات را به انبار مرکزی پیدا کند و این مقدار را در خروجی چاپ کند. # ورودی در خط اوّل ورودی به ترتیب ۴ عدد $n$ تعداد شهر‌ها، $m$ تعداد جاده‌ها، $t$ محل انبار و $c$ هزینه‌ی خرید گونی آمده است. در هر یک از $m$ خط بعدی مشخصات جاده‌ها آمده است. در هر سطر ۴ عدد می‌آید، عدد اوّل و دوم شماره‌ی دو سر آن جاده، عدد سوم برابر ظرفیت عبور جاده و عدد چهارم هزینه‌ی عبور جاده است. سپس در خطی جدید، عدد $k$ تعداد کشاورزان می‌آید. در هر یک از $k$ خط بعدی، دو عدد صحیح می‌آید. عدد اوّل محل زندگی کشاورز($v_i$) و عدد دوم مقدار محصولات کشاورز($m_i$) است. $$n, k \leq 400$$ تمامی هزینه‌ها کمتر یا مساوی $10^6$ هستند. تمامی ظرفیت‌ها و $m_i$ها نیز کم‌تر یا مساوی $400$ هستند. ## زیرمسئله‌ها | شماره‌ی زیرمساله | محدودیت‌ها | نمره | |:------------------:|:------------------:|:------:| | ۱ | $n, k \leq 50$ | ۵۰ | | ۲ | بدون محدودیت اضافی | ۵۰ | # خروجی در تنها سطر خروجی در صورتی که نتوان همه‌ی محصولات را به انبار مرکزی رساند، عبارت "No Solution" و در غیر این صورت کم‌ترین هزینه برای انجام این کار را بنویسید. # مثال ## ورودی نمونه ``` 3 3 3 2 1 2 5 2 1 3 2 2 2 3 5 2 1 1 5 ``` ## خروجی نمونه ``` 4 ```