• محدودیت زمان: ۰.۵ ثانیه
• محدودیت حافظه: ۱۲۸ مگابایت

برای کنترل جهان باید از کنترل کولر شروع کرد!

"رادزینکا دوبرامیل ویچشسلافوویچ"

قرار شده‌است که در عمارت، انتخاباتی برگزار شود تا شخص منتخب خانه را اداره کند. آقای خطری، یکی از اعضای خانه است که میخواهد برای این کار نامزد بشود. او مردی به شدت منطقی بوده و معتقد است که کولر باید خاموش باشد! انگیزه‌ی شرکت او در انتخابات هم همین است...

هنگام ثبت‌نام نامزد از او خواسته شد تا نام انتخاباتی خود را وارد کند. او که احساس می‌کرد که اسم «خطری» رای‌دهندگان را خواهد ترساند تصمیم گرفت که نام دیگری را وارد کند. او دستش را برروی صفحه کلید گذاشت (تکنولوژی در عمارت بالاست) و تعدادی کلید را فشار داد تا اسم انتخاباتی‌اش را وارد کند. می‌دانیم که صفحه کلید تنها شامل حروف و دکمه‌ی CapsLock می‌باشد و ابتدا CapsLock خاموش بوده است. با گرفتن دکمه‌هایی که آقای خطری زده است بگویید که نام انتخاباتی او چیست.

اگر CapsLock روشن باشد، حروف بزرگ نوشته خواهند شد و اگر خاموش باشد حروف کوچک نوشته خواهند شد. همچنین با زدن دکمه‌ی CapsLock، وضعیت CapsLock برعکس خواهد شد.

ورودی🔗

در سطر اول ورودی عدد $n$ آمده‌ است که نمایانگر تعداد دکمه‌هایی است که آقای خطری وارد کرده است.

سپس در $n$ سطر بعدی، در هر سطر، دکمه‌ای که آقای خطری زده است آمده است. این دکمه یا یکی از حروف کوچک انگلیسی است و یا دکمه‌ی CapsLock که دکمه‌ی CapsLock در ورودی به صورت "CAPS" آمده است.

تضمین می‌شود که حداقل یک دکمه از حروف زده شده است.

$3 \le n \le 100$

خروجی🔗

در تنها سطر خروجی نام انتخاباتی آقای خطری را خروجی دهید.

مثال🔗

ورودی نمونه ۱🔗

10
d
CAPS
a
n
g
CAPS
e
r
CAPS
y

خروجی نمونه ۱🔗

dANGerY

ورودی نمونه ۲🔗

3
z
j
u

خروجی نمونه ۲🔗

zju

• محدودیت زمان: ۰.۵ ثانیه
• محدودیت حافظه: ۱۲۸ مگابایت

رتبه‌ی ۱۶۱ سال بعد: دوره چهار حلی سه کنکور دارند!

رتبه‌ی یک پارسال: اه!اه! پس ۱۶۰ تا بذار رو رتبت!

مدتی پیش تصمیم گرفته بودم وارد بازار عرضه‌ی کتاب کنکور شوم! و این دقیقاً پس از آن بود که قیمت‌های سرسام آورش کمرم را شکسته بود! درحال حاضر$a_1$‌ شیمیِ خیلی قهوه ای و $a_2$ دیفرانسیلِ باج و $a_3$ هندسه یِ خوشخوار داریم. هر بار می‌توانیم یکی از دو کار را انجام دهیم:

1. دو تا از یک نوع را بفروشیم.
2. دو تا از انواع مختلف بدهیم و یکی از نوع دیگر پس بگیریم.

اگر در آخر دقیقاً یکی از یک نوع بماند آن از کدام نوع ها می‌تواند باشد؟

ورودی🔗

در تنها خط ورودی سه عدد $a_1$ , $a_2$, $a_3$ می آیدکه هرکدام تعداد یک نوع کتاب را معلوم می‌کند.

$0 \leq a_i \leq 1\ 000\ 000\ 000$

خروجی🔗

در تنها خط خروجی سه کلمه بنویسید و در $i$ امین کلمه معلوم کنید که آیا می‌توان طوری کار ها را انجام داد که در آخر تنها یکی از نوع $i$ بماند(و از انواع دیگر چیزی نمانده باشد). اگر ممکن بود YES، و در غیر این صورت ‍‍‍NO را چاپ کنید.

مثال🔗

ورودی نمونه ۱🔗

1 1 1

خروجی نمونه ۱🔗

NO NO NO

ورودی نمونه ۲🔗

1 1 2

خروجی نمونه ۲🔗

NO NO YES

به راحتی می‌توان با این سری اعمال به یکی از نوع سوم رسید: (1,2) (3,3)

• محدودیت زمان: ۲ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

امروز , سالگرد تأسیس شرکت رهنماست به همین منظور چنگیز که از قدیمی‌های رهنما است مأمور می‌شود تا بین برنامه‌نویسان رهنما هدایایی به رسم یادبود پخش کند. شرکت رهنما $N$ برنامه‌نویس دارد که به هر کدام یک عدد یکتا بین $1$ تا $N$ نسبت داده شده است. برای گرفتن هدایا , برنامه‌نویسان رهنما یک صف تشکیل می‌دهند و به ترتیب شماره‌شان در آن قرار می‌گیرند به این صورت که برنامه‌نویس با شماره ۱ در ابتدای صف و برنامه‌نویس با شماره $N$ در انتهای صف قرار می‌گیرد. از آنجایی که چنگیز امروز به شرکت نیامده , تیمور را برای پخش جوایز مأمور می‌کند اما از طریق تلگرام به او فرمان می‌دهد که در هر مرحله چه کاری انجام دهد.

چنگیز به شدت رفیق باز است و ممکن است در صف دست ببرد.

چنگیز دو نوع فرمان به تیمور می‌دهد :

نوع اول: به تیمور می‌گوید که به شخصی که در سر صف قرار دارد هدیه دهد و وی را به ته صف بفرستد.

نوع دوم: به تیمور می‌گوید که برنامه‌نویس شماره $i$ را پیدا کند و به سر صف بیاورد.

بدیهی است که ممکن است یک نفر چند بار جایزه بگیرد.

حال از شما می‌خواهیم با گرفتن دستورات چنگیز , بعد از هر دستور نوع اول , شماره برنامه‌نویسی که هدیه گرفته است را چاپ کنید.

ورودی🔗

در خط اول به شما دو عدد $N , C$ داده می‌شود که $N$ تعداد برنامه‌نویسان رهنماست و $C$ تعداد دستورات چنگیز است. در $C$ خط بعدی دستورات بعدی به شما داده می‌شود. در هر خط یک عدد مانند $x$ به شما داده می‌شود. اگر $x$ برابر صفر بود یعنی دستور نوع اول است در غیر اینصورت دستور از نوع دوم است و به این معناست که نفر $x$ ام باید به سر صف بیاید. $1 \le N \le 1\ 000\ 000\ 000$ $1 \le C \le 1\ 000$ $0 \le x \le N$ به محدوده $N$ توجه کنید.

خروجی🔗

به ازای هر دستور نوع اول , شما باید شماره فردی را که هدیه می‌گیرد در یک خط چاپ کنید. ( تعداد خط های خروجی برابر تعداد دستورات نوع اول می‌شود)

ورودی نمونه ۱🔗

100000 6
0 
0 
10000
0
0
20

خروجی نمونه ۱🔗

1
2
10000
3

در دو دستور اول به نفرات اول و دوم هدیه داده میشود. در دستور سوم نفر $10000$ ام به سر صف میاید. در دستور چهارم کسی که سر صف است , نفر $10000$ ام , هدیه اش را میگیرد و به ته صف میرود. در دستور پنجم نفر سوم که اکنون سر صف است هدیه میگیرد و به ته صف میرود. در دستور ششم هم نفر $20$ ام به سر صف میاید.

ورودی نمونه ۲🔗

4 6
0
1
0
3
0
0

خروجی نمونه ۲🔗

1
1
3
2

• محدودیت زمان: ۲ ثانیه
• محدودیت حافظه: ۵۱۲ مگابایت

چند روز پیش و مصادف با روز بعد از اعلام نتایج امتحان هندسه‌ی میان‌ترم، کاراکتر کمکی ۱ در انباری خانه‌شان یک صفحه بازی پیدا کرده که متعلق به پدربزرگ مرحومش (خدا رفتگان شما را هم بیامرزد) است. کاراکتر کمکی ۱ با پیداکردن این صفحه‌ی بازی بسیار خوشحال می‌شود و تصمیم می‌گیرد با دوستش کاراکتر کمکی ۲ برای این‌ صفحه‌ی بازی، بازی‌ای ابداع کنند که با انجام آن اندکی از ناراحتی و غم جان‌سوز اعلام نتایج امتحان هندسه فاصله بگیرند.

از آنجایی که قبل از این‌که قرار باشد بازی ابداع شود آن‌ها حتما باید نسبت به صفحه‌ی بازی شناخت پیدا کنند. پس به همین منظور راهنمای صفحه‌ی بازی را مطالعه می‌کنند که اطلاعات مندرج در آن به شرح زیر است:

• صفحه‌ی بازی شامل $n$ دایره و $n - 1$ پاره خط است که هر سر هر پاره‌خط به یکی از دایره‌ها متصل است.
• دایره‌های صفحه با اعداد متمایز ۱ تا $n$ شماره‌گذاری شده‌اند.
• دو دایره‌ را در صفحه‌ی بازی همسایه می‌نامیم اگر و فقط اگر یکی از پاره‌خط‌های صفحه‌ باشد که یک سر آن به یکی از این دو دایره و سر دیگرش به دایره‌ی دیگر متصل باشد.
• منظور از حرکت مهره در این صفحه‌ی بازی، حرکت دادن مهره از دایره‌ای که روی آن قرار دارد به یکی از همسایه‌های خالی از مهره‌ی آن است.
• اگر فقط یک مهره بر روی یکی از دایره‌های صفحه داشته باشیم (برخلاف شرایط بازی) تضمین می‌شود می‌توان با چندبار حرکت‌ دادن مهره، آن را به هر یک از دایره‌های دیگر صفحه رساند.

بعد از مطالعه‌ی کامل جزئیات دفترچه‌ی راهنما که در بالا آمده بود، کاراکتر کمکی ۱ و کاراکتر کمکی ۲ توانستند یک بازی بسیار مهیج برای این صفحه‌ی بازی ابداع کنند که مشخصات آن به شرح زیر است:

• بازی دو نفره است.
• هر بازیکن یک مهره‌ی مخصوص به خود دارد. (بازیکن‌ها در حین بازی می‌توانند وضعیت مهره‌ی حریف را ببینند)
• هر یک از دو مهره در ابتدا و حین بازی روی یکی از دایره‌های صفحه قرار می‌گیرند.
• هیچ‌گاه دو مهره در یک دایره قرار نمی‌گیرند.
• با شروع از کاراکتر اصلی ۱، به نوبت هر بازیکن یک‌بار مهره‌ی خود را حرکت می‌دهد.
• بازنده‌ی بازی کسی است که نتواند حرکتی انجام بدهد. یعنی دایره‌ی همسا‌یه‌ی خالی‌ای برای او وجود نداشته باشد که بتواند مهره‌اش را به آن حرکت دهد.

دارنده‌ی استراتژی برد، کسی است که با هر نوع بازی طرف مقابل، بتواند طوری بازی کند که در انتها، بازی حتما به نفع خودش تمام شود.

برنامه‌ای بنویسید که دارنده‌ی استراتژی برد در بازی را مشخص کند.

ورودی🔗

در خط اول ورودی عدد طبیعی $n$ داده می‌شود که نشان دهنده تعداد دایره‌های صفحه‌ی بازی است.

در $n -1$ خط بعدی در هر خط شماره‌ی دو دایره آمده‌اند که نشان‌دهنده‌ی وصل‌بودن این دو دایره توسط یکی از پاره‌خط‌های صفحه است.

در خط آخر دو عدد طبیعی $x$ و $y$ داده می‌شود که به ترتیب نشان‌دهنده‌ی شماره دایره‌ی محل ابتدایی مهره‌ی کاراکتر کمکی ۱ و کاراکتر کمکی ۲ است.

$2 \leq n \leq 100 \ 000$

خروجی🔗

در تنها خط خروجی اگر کاراکتر کمکی ۱ دارنده‌ی استراتژی برد است، karakter e komaki_1 را چاپ کنید و اگر کاراکتر کمکی ۲ دارنده‌ی استراتژی برد است، karakter e komaki_2 را چاپ کنید.

مثال🔗

ورودی نمونه ۱🔗

3
1 2
1 3
1 2

خروجی نمونه ۱🔗

karakter e komaki_2

ورودی نمونه ۲🔗

4
1 2
1 3
1 4
3 1

خروجی نمونه ۲🔗

karakter e komaki_2

ورودی نمونه ۳🔗

7
1 2
1 6
2 3
2 4
2 5
6 7
3 7

خروجی نمونه ۳🔗

karakter e komaki_1

توضیح🔗

در مثال اول مهره‌های کاراکتر کمکی ۱ و کاراکتر کمکی ۲ به ترتیب در دایره‌های ۱ و ۲ قرار دارند. در حرکت اول کاراکتر کمکی ۱ تنها می‌تواند به دایره‌‌ی ۳ برود. در حرکت بعدی کاراکتر کمکی ۲ نیز تنها یک حرکت دارد و می‌تواند به دایره‌ی شماره‌ی ۱ برود. حرکت بعدی نوبت کاراکتر کمکی ۱ است که هیچ دایره‌ی همسایه‌ی خالی ندارد، پس برنده‌ی بازی کاراکتر کمکی ۲ است.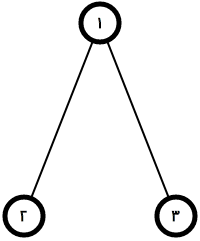

در مثال دوم مهره‌های کاراکتر کمکی ۱ و کاراکتر کمکی ۲ به ترتیب در دایره‌های ۳ و ۱ قرار دارند. در حرکت اول کاراکتر کمکی ۱ هیچ حرکتی نمی‌تواند انجام بدهد و در همین حرکت اول و بدون هیچ حرکت مهره‌ای کاراکتر کمکی ۲ برنده‌ی بازی است.

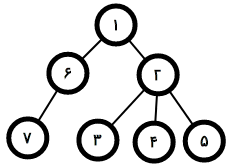
در مثال سوم مهره‌های کاراکتر کمکی ۱ و کاراکتر کمکی ۲ به ترتیب در دایره‌های ۳ و ۷ قرار دارند. در حرکت اول کاراکتر کمکی ۱ مجبور است مهره‌اش را به دایره‌ی ۲ ببرد. در حرکت بعدی کاراکتر کمکی ۲ هم مجبور است مهره‌اش را به دایره‌ی ۶ ببرد. از این‌جا به بعد که برای هر یک از دو بازیکن چند حرکت ممکن وجود دارد، برای کاراکتر کمکی ۱ روش برد ارائه می‌دهیم. کاراکتر کمکی ۱ می‌تواند مهره‌اش را به دایره‌ی ۱ ببرد تا کاراکتر کمکی ۲ را مجبور کند در مرحله‌ی بعد مهره‌اش را به دایره‌ی ۷ ببرد و در حرکت آخر کاراکتر کمکی ۱ مهره‌اش را به دایره‌ی ۶ می‌برد تا کاراکتر کمکی ۲ حرکت ممکنی در نوبتش نداشته باشد و برنده‌ی بازی کاراکتر کمکی ۱ شود.

• محدودیت زمان: ۲ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

برای کنترل جهان باید از کنترل کولر شروع کرد.

«رادزینکا دوبرامیل ویچشسلافوویچ»

متاسّفانه یا خوش‌بختانه آقای خطری نتوانست ترامپولین درستی را انتخاب کند و تلاش‌های شبانه‌روزی‌ش برای مذاکره با آقای بی‌خطر به شکست منتهی شد. پس منشی او تصمیم گرفت مستقیماً با طرفداران آقای بی‌خطر صحبت کند. شایان ذکر است آخرین اخبارِ موجود حاکی از آن است که دو نامزد شهیر انتخابات، همچنان در حال پرش بر روی ترامپولین‌ها هستند و تلاش‌ها در پی نجاتشان هنوز ادامه دارد.

در عمارت هر فرد رای دهنده یک درجه‌ی اجتماعی دارد و تعداد افرادی که درجه‌ی اجتماعی‌شان $i$ است، دقیقن $i$ نفر است. ($1 \leq i \leq n$) نحوه‌ی رای دادن افراد هر درجه، از روی رای افراد درجه‌ی بعدی آن‌ها مشخّص می‌شود؛ به استثنای افراد درجه $n$ که مقام بسیار والایی دارند و خودشان مشخّص می‌کنند که به چه کسی رای بدهند.

مثلاً در صورتی که $n = 4$ رای فرد درجه ۱ از روی افراد درجه ۲ مشخّص می‌شود، که رای خود آن‌ها از روی افراد درجه ۳ مشخّص می‌شود. رای افراد درجه ۳ نیز از روی افراد درجه ۴ مشخّص می‌شود. امّا افراد درجه‌ ۴ رایشان مستقل از رای بقیّه مشخّص خواهد شد.

فرد $i$اُم از درجه‌ی $j$اُم($1 \leq i \leq j < n$) تنها در صورتی به آقای خطری رای می‌دهد که حداقل یکی از افراد $i$اُم و $i+1$ام از درجه‌ی $j + 1$اُم قصد داشته باشند به آقای خطری رای دهند.

در این میان منشی آقای خطری می‌‌تواند با حداکثر $k$ تا از افراد صحبت کند و رای آن‌ها را عوض کند. اگر رای کسی عوض شود، رای تمام افرادی که رایشان بستگی به رای او داشت نیز طبق تعریف پاراگراف قبل به روز رسانی خواهد شد.

به شما $n$ و $k$ و آرای اوّلیّه‌ی افراد با درجه‌ی اجتماعی $n$ داده می‌شود و باید بگویید اگر منشی آقای خطری به صورت بهینه افرادی را برای صحبت کردن انتخاب کند، چند نفر به آقای خطری رای خواهند داد.

ورودی🔗

در اوّلین خط ورودی به ترتیب دو عدد صحیح $n$ و $k$ آمده است که با یک کاراکتر space از هم جدا شده‌اند.

در خط دوم رشته‌ای به طول $n$ خواهد آمد؛ حرف $i$اُم آن در صورتی که برابر 'K' باشد یعنی فرد $i$اُم از درجه‌ی $n$ به طور پیش‌فرض به آقای خطری رای می‌دهد و در صورتی که برابر 'B' باشد یعنی آن فرد به طور پیش‌فرض به آقای بی خطر رای می‌دهد.

$1 \le n \le 500$ $0 \le k \le 500$

خروجی🔗

در تنها خط خروجی جواب مطلوب مساله را چاپ کنید.

مثال🔗

ورودی نمونه ۱🔗

3 0
BKK

خروجی نمونه ۱🔗

5

ورودی نمونه ۲🔗

3 1
BKK

خروجی نمونه ۲🔗

6

ورودی نمونه ۳🔗

6 1
BBBBBB

خروجی نمونه ۳🔗

12