+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۶۴ مگابایت
----------
مارچلو که عاشق تابستان است، تصمیم گرفته که این تابستان را تبدیل به یکی از رویاییترین تابستانهای زندگیاش کند. برای همین میخواهد که با یک نوبرانهی تازه، تابستان رویایی خودش رو شروع کند!
مارچلو به مغازهی هندوانه فروشی آلبرتو میرود و پنج عدد هندوانه از او میخرد. از آنجایی که همهی هندوانهها همیشه قرمز نیستند، میزان قرمز بودن هندوانهی $i$اُم $a_i$ است که عددی بین ۰ تا ۱۰۰ است.
مارچلو وقتی به خانه میرسد، همهی هندوانهها را میشکند تا ببیند هندوانههای آلبرتو چقدر میارزند. او پس از شکاندن همهی هندوانهها یکی از وضعیتهای زیر را مشاهده میکند:
+ اگر **حداقل سه هندوانه** میزان قرمزی **بیشتر یا مساوی ۸۰** داشتند، مارچلو خوشحال خواهد شد.
+ اگر **حداقل یک و حداکثر دو** هندوانه میزان قرمزی **بیشتر یا مساوی ۸۰** داشتتند، مارچلو راضی خواهد بود.
+ در غیر این صورت مارچلو عصبانی خواهد شد.
از آنجایی که مارچلو تحمل عصبانی شدن را ندارد، از شما میخواهد تا پیش از شکاندن هندوانهها، نتیجه را به او بگویید.
# ورودی
ورودی تنها شامل یک خط است که در آن به ترتیب پنج عدد $a_1, a_2, a_3, a_4, a_5$ با فاصله از هم آمده است.
$$0 \le a_1,a_2,a_3,a_4,a_5 \le 100$$
# خروجی
خروجی تنها شامل یک خط است. در صورتی که مارچلو پس از شکاندن هندوانهها خوشحال میگشت عبارت `Mamma mia!`، در صورتی که پس شکاندن آنها راضی بود، عبارت `Mamma mia!!` و در غیر این صورت عبارت `Mamma mia!!!` را چاپ کنید.
## ورودی نمونه ۱
```
70 80 90 10 95
```
## خروجی نمونه ۱
```
Mamma mia!
```
از آنجایی که سه هندوانه با میزان قرمزی بیشتر یا مساوی ۸۰ داریم، مارچلو خوشحال خواهد شد.
## ورودی نمونه ۲
```
50 90 10 20 50
```
## خروجی نمونه ۲
```
Mamma mia!!
```
از آنجایی که یک هندوانهی با میزان قرمزی بیشتر یا مساوی ۸۰ داریم، مارچلو راضی خواهد شد.
## ورودی نمونه ۳
```
0 79 10 30 25
```
## خروجی نمونه ۳
```
Mamma mia!!!
```
از آنجایی که هیچ هندوانهای با میزان قرمزی بیشتر یا مساوی ۸۰ نداریم، مارچلو عصبانی خواهد شد.
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۶۴ مگابایت
----------
مارچلو پس از خوردن هندوانهها به سوی جشنوارهی "تابستونهای رویایی" رفت تا یک مرحله به رویایی کردن تابستان خود نزدیک شود!
مارچلو در آن جشنواره شروع به فروش پنکیک کرد. در ابتدای کار، او $n$ پنکیک داشت که میخواست آنها را بفروشد. همچنین $n$ مشتری گرسنه منتظر خرید پنکیکها بودند. مارچلو که میخواست درصد رضایت مشتریها را بالا ببرد، تصمیم گرفت تعدادی از مشتریها را انتخاب کند و به هر یک از آنها **به تعداد یکسان** و **بیش از یک عدد** پنکیک بفروشد و در ازای آن یک سکه از هر نفر دریافت کند. علاوه بر آن، از آنجایی که مارچلو دورریز را دوست ندارد، تصمیم داشت تا تمام $n$ پنکیک را بفروشد.
از آنجایی که مارچلو برای ساخت تابستان رویایی خود نیاز به پول دارد، از شما میخواهد که به او بگویید بیشترین تعداد سکهای که میتواند دریافت کند به صورتی که شرایط بالا را رعایت کند چقدر است.
# ورودی
ورودی تنها شامل یک خط است که در آن عدد $n$ آمده است.
$$2 \le n \le 1\ 000$$
# خروجی
در تنها خط خروجی بیشترین سودی که مارچلو میتواند از فروش پنکیکها به دست آورد را چاپ کنید.
## ورودی نمونه ۱
```
6
```
## خروجی نمونه ۱
```
3
```
مارچلو میتواند سه نفر از مشتریان را انتخاب کند و به هر یک دو پنکیک بفروشد و به این ترتیب سه سکه دریافت کند.
## ورودی نمونه ۲
```
5
```
## خروجی نمونه ۲
```
1
```
مارچلو میتواند یک نفر از مشتریان را انتخاب کند و پنج پنکیک به او بفروشد و به این ترتیب یک سکه دریافت میکند.
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
مارچلو پس از به جیب زدن فراوان از فروش پنکیکها، تصمیم گرفت برای ساخت تابستان رویایی خود تکانی بخورد و اندکی ورزش کند. از آنجایی که خیلی امکانات نداشت با پیاده روی در پیادهروی جلوی خانهاش شروع کرد.
پیادهروی جلوی خانهی مارچلو به شکل نواری با $n$ خانه است که هر یک از خانهها سیاه یا سفید میباشد. او که آرام و قرار ندارد در هر دقیقه از خانهی فعلی خود به خانهی مجاور میرود البته به این شرط که رنگ آن خانه با خانهی فعلیاش متفاوت باشد.
او که برای این کار بسیار ذوقزده است از شما میخواهد برای هر یک از $q$ حالتی که در ذهن خود دارد بگویید آیا میتواند از خانهی مبدأ مورد نظرش شروع و با رعابت شرایط بالا، در خانهی مقصد مورد نظرش تمام کند یا خیر.
# ورودی
در خط اول ورودی $n$ و $q$ آمده که به ترتیب نشاندهندهی تعداد خانهها و تعداد حالات در ذهن مارچلو است.
$$2 \le n \le 100\ 000$$
$$1 \le q \le 100\ 000$$
در خط دوم ورودی $n$ عدد آمده که اگر عدد $i$ام برابر صفر باشد خانهی $i$ام سفید و در غیر این صورت سیاه است.
در خط $i$ام از $q$ خط بعدی دو عدد $s_i$ و $e_i$ آمده که خانهی شروع و پایان مورد نظر مارچلو است.
$$1 \le s_i, e_i \le n$$
$$s_i \neq e_i$$
# خروجی
خروجی $q$ خط دارد. اگر مارچلو میتوانست پیاده رویاش را از خانهی $s_i$ شروع و در خانهی $e_i$ به پایان برساند در خط $i$اُم عبارت `YES` و در غیر این صورت `NO` چاپ کنید.
## ورودی نمونه ۱
```
5 3
0 1 0 0 1
1 3
2 4
4 5
```
## خروجی نمونه ۱
```
YES
NO
YES
```
در حالت دوم مارچلو نمیتواند پیاده رویاش را از خانهی ۲ شروع و در خانهی ۴ تمام کند. در دو حالت دیگر میتوان دنباله حرکتی ارائه داد که این کار ممکن باشد.
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
پس از جستوخیز بسیار مارچلو تصمیم گرفت آلبرتو را به خانهاش دعوت کند تا با هم جشن بگیرند. او قصد دارد سیستم آب نمای حیاط خانهاش را به رخ آلبرتو بکشد، اما از آنجایی که دیر به فکر افتاده، از شما درخواست کمک دارد!
مارچلو نقشهی شبکهی آبرسانی آب نما را در اختیار شما میگذارد. این شبکه را میتوان با گرافی جهتدار و همبند نشان داد (بدون در نظر گرفتن جهت یالها) که هر رأس در آن **دقیقاً** یک لولهی خروجی دارد (ممکن است سر دیگر لولهی خروجی به خود رأس متصل باشد). نحوهٔ جابهجایی آب به این صورت است که اگر در دقیقهی $t$ مقداری آب در رأسی مانند $u$ قرار داشته باشد در دقیقهی $t+1$ تمام این آب از طریق لولهی خروجی رأس $u$ به سر دیگر لوله انتقال مییابد.
مارچلو ابتدا در همهی رأسهایی که لولهی ورودی ندارند مقداری آب میریزد (فرض کنید زمانی که صرف این کار میشود ناچیز است) و منتظر میماند تا آبنما ثابت شود **یعنی زمانی که از آن به بعد هر رأسی که در آیندهای دور (مثلاً** $10^{100}$ **دقیقه) حداقل یک بار از آن آب بگذرد اکنون نیز آب داشته باشد.** (ممکن است رئوسی علاوه بر آنها هم آب داشته باشند) همچنین او میخواهد آلبرتو هنگامی که به خانهی او میآید، آب نما را ثابت ببینند. به مارچلو کمک کنید بفهمد آب نما حداقل چند دقیقه بعد از اینکه او در رأسها آب میریزد، ثابت میشود.
# ورودی
در خط اول ورودی عدد $n$ آمده است که نمایانگر تعداد رأسهای شبکهی آبرسانی است.
$$2 \le n \le 100\ 000$$
در خط دوم ورودی $n$ عدد آمده که عدد $i$ام ($o_i$) شمارهی رأسی است که لولهٔ خروجی از رأس $i$ بدان متصل است. (آب از راس $i$ به راس $o_i$ میریزد)
$$1 \le o_i \le n$$
**تضمین میشود در ابتدا در حداقل یکی از رأسها آب وجود دارد.**
# خروجی
کمینه دقیقهای که از آن به بعد آب نما همیشه ثابت است را در تنها خط خروجی چاپ کنید (فرض کنید مارچلو در دقیقهی صفرم، در راسهای فاقد لولهی ورودی آب میریزد) اگر چنین زمانی وجود نداشت عبارت `no party` را خروجی دهید.
## ورودی نمونه ۱
```
5
2 3 1 3 2
```
## خروجی نمونه ۱
```
no party
```
از آنجا که مجموعهی رأسهایی که آب در آنها هست هیچوقت ثابت نمیشود، پاسخ برابر `no party` است.
## ورودی نمونه ۲
```
7
2 3 1 1 2 1 6
```
## خروجی نمونه ۲
```
2
```
پس از گذشت دو دقیقه، در رئوس شمارهی ۱ و ۲ و ۳ آب خواهد بود و پس از آن نیز در همان رئوس، آب باقی خواهد ماند، برای همین پاسخ برابر دو خواهد بود.
## ورودی نمونه ۳
```
8
2 3 1 3 1 2 1 7
```
## خروجی نمونه ۳
```
1
```
در ابتدا (دقیقهی ۰) رئوس $4,5,6,8$ پر از آب هستند، سپس بعد از یک دقیقه رئوس $1,2,3,7$ و از آن به بعد همواره رئوس $1,2,3$، در نتیجه اولین جایی که رئوس $1,2,3$ آمدهاند یعنی دقیقهی ۱ زمان مورد نظر است.
+ محدودیت زمان: ۳.۵ ثانیه
+ محدودیت حافظه: ۵۱۲ مگابایت
----------
مارچلو که سال سختی را سپری کرده، بسیار خسته است. پس تصمیم گرفته که در این تابستان قوای از دست رفتهٔ خود را بازیابی کند و چه کاری بهتر از یک مسافرت خوب و مقداری جهانگردی!
زمینی که مارچلو در آن زندگی میکند تخت است! به طور دقیقتر جدولی $n \times m$ میباشد که هر خانهی آن یا منطقهی آزاد است و یا توسط کشوری اداره میشود. (توجه کنید لزومی ندارد مناطق تحت کنترل یک کشور مجاور یکدیگر باشند) او در هر مرحله میتواند به یکی از خانههای مجاور ضلعی خانهی فعلی سفر کند.
همچنین سفر در مناطق آزاد برای همگان مجاز است اما برای سفر در مناطق یک کشور نیاز به پاسپورت آن کشور داریم. هر کشور نیز تعدادی سفارت در مناطق آزاد دارد که میتوان پاسپورت آن کشور را از آنها اخذ کرد. با دریافت پاسپورت جدید پاسپورت قدیمی از بین خواهد رفت. **گرفتن پاسپورت یک کشور هیچ هزینهای ندارد اما برای وارد شدن از منطقهی آزاد به منطقهی آن کشور باید یک واحد هزینهی عوارض ورود بپردازیم.**
حال مارچلو میخواهد از خانهی خود در جدول شروع کند و مسافرتش را در خانهی مقصدی که از قبل معلوم کرده به پایان برساند. به او کمک کنید با کمترین هزینه سفرش را انجام دهد. (یا بگویید که نمیتواند به مقصد برسد) **تضمین میشود خانهی مارچلو در منطقهی آزاد است و در ابتدا پاسپورت هیچ کشوری را ندارد.**
# ورودی
در خط اول به ترتیب اعداد $n, m, k$ آمده است که نشان دهندهی طول جدول، عرض جدول و تعداد سفارتها است.
در خط دوم اعداد $ s_x, s_y, e_x, e_y $ آمده که مختصات خانهی شروع و پایان مارچلو است.
$$1 \le n, m \le 500$$
$$1 \le k \le 10^6$$
$$1 \le s_x, e_x \le n$$
$$1 \le s_y, e_y \le m$$
**تصمین میشود خانهی ابتدایی و انتهایی یکی نیستند و تمام سفارتها در مناطق آزاد هستند.**
در هر یک از $n$ خط بعدی $m$ عدد آمده که عدد $j$ام در سطر $i$ام برابر با $a_{i,j}$ و نشان دهندهی کشوری است که خانهی $(i, j)$ را اداره میکند. (اگر این عدد صفر باشد، به این معناست که آن خانه منطقهی آزاد است)
$$0 \le a_{i,j} \le 10^6$$
سپس در هر یک از $k$ خط بعدی سه عدد $x, y, p$ آمده که نشان دهندهی وجود سفارت کشور $p$ در خانهی $(x, y)$ است.
$$1 \le x \le n$$
$$1 \le y \le m$$
$$1 \le p \le 10^6$$
# خروجی
اگر رسیدن به مقصد ممکن نبود `-1` و در غیر این صورت کمینه هزینهی ممکن برای رسیدن به مقصد را چاپ کنید.
## ورودی نمونه ۱
```
4 4 2
1 1 4 4
0 0 1 2
0 2 2 2
0 1 1 2
1 1 1 2
1 2 1
2 1 2
```
## خروجی نمونه ۱
```
1
```
میتوان با گرفتن پاسپورت کشور ۲ در خانهی $(1 ,2)$ و سپس رفتن به $(2 ,2)$ با یک هزینه وارد مناطق کشور ۲ شد و به مقصد رسید.
## ورودی نمونه ۲
```
4 4 1
1 1 4 4
0 0 1 2
0 2 2 2
1 1 0 0
1 1 1 2
1 2 2
```
## خروجی نمونه ۲
```
2
```
مارچلو کافی است ابتدا پاسپورت کشور ۲ را در خانهی $(1,2)$ بگیرد سپس با یک هزینه به $(2,2)$ رفته و با گذشت از $(2,3)$، $(3,3)$ و $(3,4)$ با یک هزینه وارد $(4,4)$ شده و به مقصد برسد. **توجه کنید تا زمانی که مارچلو پاسپورت جدیدی نگیرد پاسپورت قبلیاش برایش باقی میماند.**
+ محدودیت زمان: ۲ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
مارچلو در هنگام سپری کردن مسافرت رویایی خود بود که متوجه فقدانی در اوقات فراغت خود شد و آن چیزی نبود جز بازی بیلیارد! مارچلو که در این بازی تبحر خاصی داشت به سوی آلبرتو رفت تا توپهای بیلیارد را از او تحویل بگیرد. آلبرتو که به این راحتیها به کسی توپ بیلیارد نمیداد، از او خواست که مسئله زیر را برایش حل کند!
آلبرتو در کل $\binom{n+1}{2}$ توپ بیلیارد دارد که در $n$ ردیف و در زیر هم چیده شدهاند. به طور دقیقتر در ردیف $i$اُم، $i$ توپ بیلیارد طوری قرار گرفتهاند که به جز توپهای ردیف پایین، هر توپ بر روی دو توپ دیگر قرار گرفته است.
اما از آنجایی که آلبرتو توپهای یک رنگ را دوست ندارد، برای همین تصمیم گرفته است که توپهای خود را رنگ کند. برای این کار، او توپهای ردیف پایین را با سیاه یا سفید رنگ میکند و سپس رنگ توپهای بالاتر را به صورت زیر بدست میآورد:
+ اگر رنگ دو توپ موجود در زیر توپ مورد نظر برابر باشد، رنگ توپ بالایی **سفید** میشود.
+ در غیر این صورت رنگ توپ مورد نظر **سیاه** خواهد شد.
برای مثال، شکل زیر مثالی برای $n = 4$ است که در ردیف پایین آن، سه توپ به رنگ سیاه درآمدهاند:
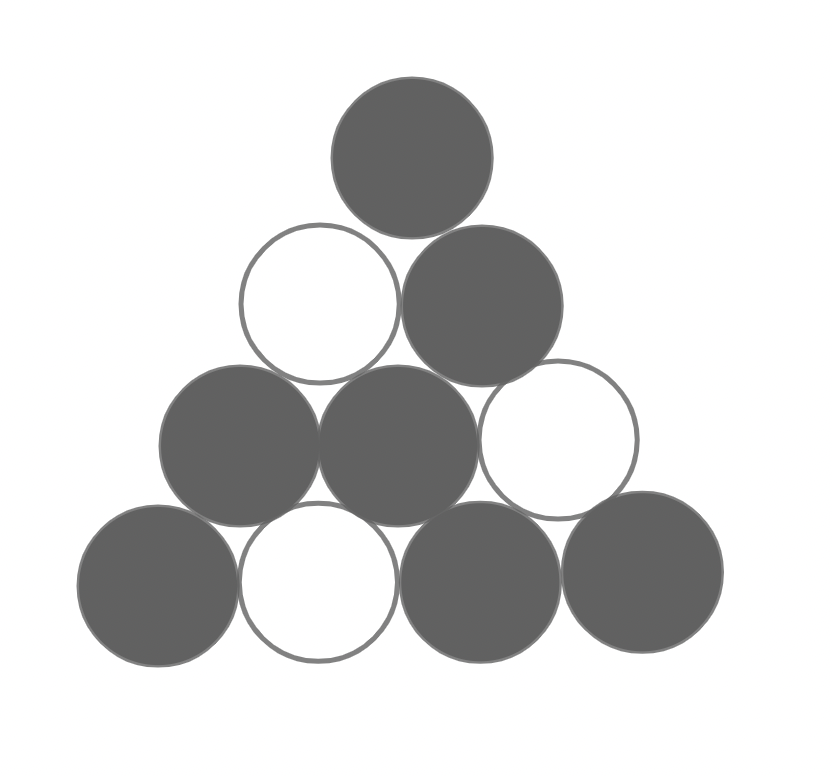
حال آلبرتو $p$ توپ از پایینترین ردیف توپهای خود را به رنگ سیاه در میآورد. سپس در $k$ مرحله، در هر مرحله به احتمال برابری، دو توپ از $n$ توپ موجود در ردیف آخر را انتخاب میکند و جای آنها را عوض میکند و پس از $k$ مرحله، رنگ توپهای دیگر را به دست میآورد. اکنون آلبرتو از مارچلو میخواهد تا احتمال این را محاسبه کند که پس از $k$ مرحله، توپ ردیف اول سیاه شود.
# ورودی
ورودی شامل دو خط است که در خط اول به ترتیب اعداد $n$ و $k$ و $p$ با فاصله از هم آمدهاند و در خط دوم $p$ عدد با فاصله از هم آمده است که عدد $i$اُم نشاندهندهی $a_i$ است و به این معناست که توپ $a_i$اُم در ردیف آخر توپهای آلبرتو سیاه است.
$$1 \le k \le 10^9$$
$$2 \le n \le 10^9$$
$$1 \le p \le 100$$
$$1 \le a_i \le n$$
**تضمین میشود $a_i$ها متمایز و صعودیاند.**
# خروجی
در تنها خط خروجی احتمال خواسته شده را به پیمانهی $10^9+7$ خروجی دهید. (میتوان ثابت کرد احتمال این واقعه برابر با عبارت $\frac{P}{Q}$ است که در آن $P$ و $Q$ نسبت به هم اول هستند. شما باید مقدار $P \times Q^{-1}$ را به پیمانهی $10^9 + 7$ خروجی دهید)
## ورودی نمونه ۱
```
2 1 2
1 2
```
## خروجی نمونه ۱
```
0
```
همواره دو توپ ردیف آخر سیاهاند پس توپ ردیف اول بعد از هر تعداد مرحله سفید است.
## ورودی نمونه ۲
```
3 2 2
1 2
```
## خروجی نمونه ۲
```
666666672
```
میتوان محاسبه کرد که احتمال سیاه شدن توپ ردیف اول پس از دو مرحله $\frac{2}{3}$ است که به باقی ماندهی $10^9+7$ برابر با مقدار بالا میشود.
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
مارچلو در انتهای سفر خود، راه برگشت را گم میکند و وارد جنگلی عجیب میشود!
درختان آن جنگل، همگی به شکل یک [درخت جستجوی دودویی](https://fa.wikipedia.org/wiki/%D8%AF%D8%B1%D8%AE%D8%AA_%D8%AC%D8%B3%D8%AA%D8%AC%D9%88%DB%8C_%D8%AF%D9%88%D8%AF%D9%88%DB%8C%DB%8C) $n$ رأسی بودند که رئوس آن با ۱ تا $n$ شمارهگذاری شده بودند!
مارچلو که با دقت بیشتری به درختهای آن جنگل نگاه کرد، متوجه شد که برخی از رأسهای آنها رنگی هستند. ویژگی این رأسها این است که اگر یک درخت جستجوی دودویی را از یک رأس رنگی ریشهدار کنیم، میتوان طوری جای بچههای رئوس (بچههای چپ و راست) را جابهجا کرد که همچنان یک درخت جستجوی دودویی باقی بماند. (در هنگام جابهجایی بچههای یک رأس، جای کل زیر درختهای آنها با هم عوض میشوند) برای مثال با جابهجا کردن بچههای رأس ۶ و سپس بچههای رأس ۴ در درخت دودویی عکس سمت چپ، به درخت جستجوی دودویی در عکس سمت راست خواهیم رسید:
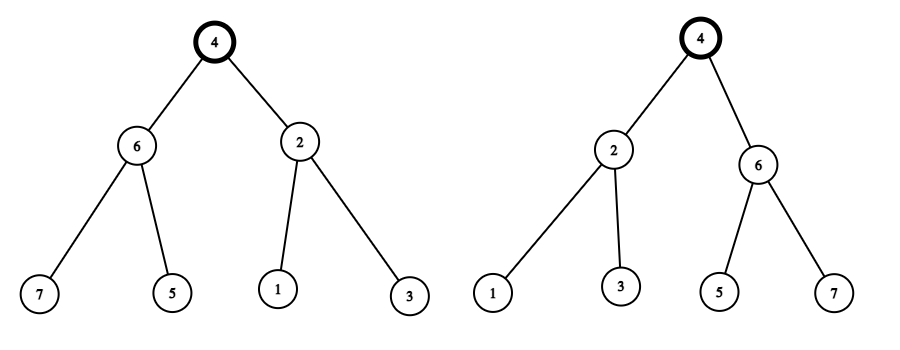
مارچلو که فهمیده بود تمام درختهای آن جنگل دقیقاً $k$ رأس رنگی دارند، میخواست بداند که حداکثر چند درخت مختلف میتواند در آن جنگل وجود داشته باشد. (دو درخت با برچسبگذاری یکسان اما ریشهی متفاوت مختلف محسوب میشوند) از آنجا که این عدد ممکن است خیلی بزرگ شود، از شما میخواهد که باقیماندهی تقسیم این عدد بر $10^9 + 7$ را به او بگویید.
# ورودی
ورودی تنها شامل یک خط است که به ترتیب دو عدد $n$ و $k$ با فاصله از هم آمده است.
$$1 \le n, k \le 100\ 000$$
$$k \le n$$
# خروجی
در تنها خط خروجی، باقیماندهی تقسیم تعداد درختهای جستجوی دودویی $n$ رأسی که دقیقاً $k$ رأس رنگی دارند را بر $10^9 + 7$ چاپ کنید.
## ورودی نمونه ۱
```
2 1
```
## خروجی نمونه ۱
```
0
```
هر درخت جستجوی دودویی دو رأسی دقیقاً دو رأس رنگی دارد، پس جواب برابر صفر خواهد بود.
## ورودی نمونه ۲
```
3 1
```
## خروجی نمونه ۲
```
2
```
تنها درختهای جستجوی دودویی سه رأسی که دقیقاً یک رأس رنگی دارند در شکل زیر آمدهاند:
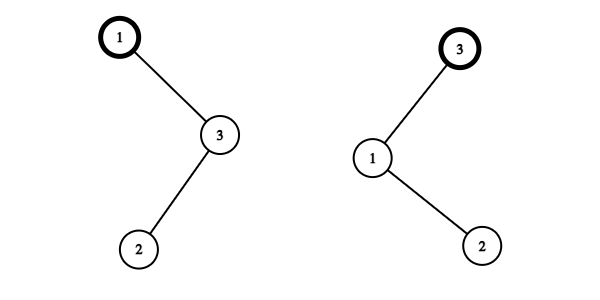
## ورودی نمونه ۳
```
3 2
```
## خروجی نمونه ۳
```
0
```
از آنجا که هر درخت جستجوی دودویی سه رأسی یا دقیقاً یک رأس رنگی و یا دقیقاً سه رأس رنگی دارد، پاسخ برابر با صفر خواهد بود.