+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
ازونجایی که دوره ی پارسال که گذشت حضوری نبود و به بچه ها خیلی خوش نگذشت شازززیا تصمیم گرفتن بچه های دوره رو یه بار دیگه دور هم جمع کنن تا هم یه دست فوتبال بزنن هم اینکه بالاخره شام طلاشونو بدن.
از اونجایی که یه تعدادی از بچه ها سر تشکیل تیم فیس و افاده ی زیادی داشتن به توافق نرسیدن و برنامه داشت بهم میریخت. بچه ها شروع کردن به دعوا... یه سریا قهر کردن رفتن... بعضیا نشستن گریه کردن... فقط هم حاج داوود بود که داشت از منظره لذت میبرد... خلاصه... . آخرم هیچ کس نمیدونست که فوتبال برگزار میشه یا اینم یه نقشه ای بوده که باز شام طلا رو بپیچونن.
تا اینکه ریش سفید شازززیا آقاتیزی سر رسید و تصمیم گرفت جوری تیم کشی بکندشون که همه خوشحال بشن تهشم بتونه شام طلا رو ازشون بکنه. آقاتیزی به بچه ها از $1$ تا $n$ شماره داد. نفر $i$ ام میگه که اگه تیم من کمتر از $a_i$ عضو داشته باشه ناراحت میشم.
حالا جدا از راضی کردن بچه ها آقاتیزی میخواست تعداد تیما رو زیاد کنه (هیچ کسم نمیدونه فازش چیه). ازونجایی که آقاتیزی بازنشست شده و نمیتونه این مسئله رو حل کنه به کمک شما نیاز داره.
# ورودی
در سطر اول ورودی عدد $n$ اومده. (تعداد بچه ها)
$$ 1 \le n \le 10^6 $$
در خط $i$ ام از $n$ خط بعدی، عدد $a_i$ اومده. (حداقل اندازه ی تیمی که نفر $i$ ام ناراحت نشه)
$$ 1 \le a_i \le n $$
# خروجی
در خط اول خروجی بیشترین تعداد تیم ها رو چاپ کنید.
# زیرمسئلهها
| زیرمسئله | نمره | محدودیت
|:------------------:|:----------:|:------------------:|
| ۱ | ۵۰ | $$ n \le 5000 $$ |
| ۲ | ۵۰ | بدون محدودیت اضافی |
# مثال
## ورودی نمونه ۱
```
5
2
1
2
2
3
```
## خروجی نمونه ۱
```
2
```
+ محدودیت زمان: ۲ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
شازززیا دارن یه سری آزمون واسه بچه ها آماده میکنن. ازونجایی خیلی پاش زحمت کشیدن دوس دارن که کلی تبلیغش کنن تا همه بچه ها توش شرکت کنن و میخوان تو شازززلند لوگوی آزموناشونو پخش کنن و برا این کار تصمیم گرفتن از کل ساختمونای خیابون اصلی بعنوان بخشی از لوگو استفاده کنن.
لوگو به شکل یه سری راه راه عمودیه با $n$ تا خط که طول هاشون متفاوته و از چپ به راست با $1$ تا $n$ شماره گذاری شده. لوگو با یه جایگشت به شکل $ (s_1, s_2, .... , s_n)$ از اعداد $1$ تا $n$ نمایش داده میشه به طوری که خط شماره ی $s_1$ کوتاه ترین خط باشه بعد از اون بین سایر خط ها خط شماره ی $s_2$ کوتاه ترین باشه و الی آخر تا اینکه خط شماره ی $s_n$ بلند ترین باشه. طول واقعی خط ها اهمیت خاصی نداره. (صرفا اون ترتیبشون مهمه)
تو خیابون اصلی شازززلند $m$ تا ساختمون وجود داره که طول هاشون متفاوته. حالا شازززیا که اینو به شکل یه سوال الگوریتمی میدیدن تصمیم گرفتن تعداد بازه هاییو پیدا کنن که لوگو با ساختمون های اون بازه مچ میشه.
اما ازون جایی که شازززیا مشغول آماده کردن سوالا هستن نمیتونن خودشون این سوالو حل کنن پس بهشون کمک کنید که تعداد بخش های پیوسته از دنباله ی ساختمون ها رو که با لوگو مچ میشه پیدا کنن. یه دنباله ی پیوسته از ساختمون ها با لوگو مچ میشه اگر ساختمون شماره ی $s_1$ بین دنباله کوتاه ترین باشه و بعد ساختمون شماره ی $s_2$ دومین کوتاه ترین باشه (یعنی بین همه ی ساختمون ها بجز ساختمون شماره ی $s_1$ کوتاه ترین باشه) و الی آخر تا ساختمون شماره $s_n$ که بلندترین باشه. برای مثال یه دنباله از ساختمون ها با ارتفاع های $5,10,4$ با لوگویی مچ میشه که بشکل جایگشت $(3,1,2)$ باشه، از اونجایی که ساختمون شماره ی $3$ با ارتفاع $4$ از همه کوتاه تره و ساختمون شماره ی $1$ دومین کوتاه ترینه و ساختمون شماره ی $2$ بلندترینه.
# ورودی
در سطر اول ورودی دو عدد $n$ (تعداد خط های لوگو) و $m$ (تعداد ساختمونای خیابون اصلی شازززلند) اومده.
$$ 2 \le n \le m \le 10^6 $$
در سطر دوم ورودی جایگشت $s$ که لوگو باهاش نشون داده میشه اومده. (جایگشت از اعداد $1$ تا $n$ می باشد)
اگر $ i \neq j $ آنگاه $ s_i \neq s_j $ میباشد.
$$ 1 \le s_i \le n $$
در سطر سوم ورودی $m$ تا عدد اومده که $h_i$ ارتفاع ساختمون $i$ ام تو خیابون اصلیه. همه ی $h_i$ ها متفاوتند.
$$ 1 \le i \le m $$$$1 \le h_i \le 10^6 $$
# خروجی
در تنها سطر خروجی تعداد زیربازه های زیبا رو چاپ کنید.
# زیرمسئلهها
| زیرمسئله | نمره | محدودیت
|:------------------:|:----------:|:------------------:|
| ۱ | ۲۰ | $$ n \le 5000\ ,\ m \le 20000$$ |
| ۲ | ۳۰ | $$ n \le 50000\ ,\ m \le 200000$$ |
| ۳ | ۳۰ | آرایه $h$ حداکثر $3×10^6$ نابهجایی دارد |
| ۴ | ۲۰ | بدون محدودیت اضافی |
# مثال
## ورودی نمونه ۱
```
5 10
2 1 5 3 4
5 6 3 8 12 7 1 10 11 9
```
## خروجی نمونه ۱
```
2
```
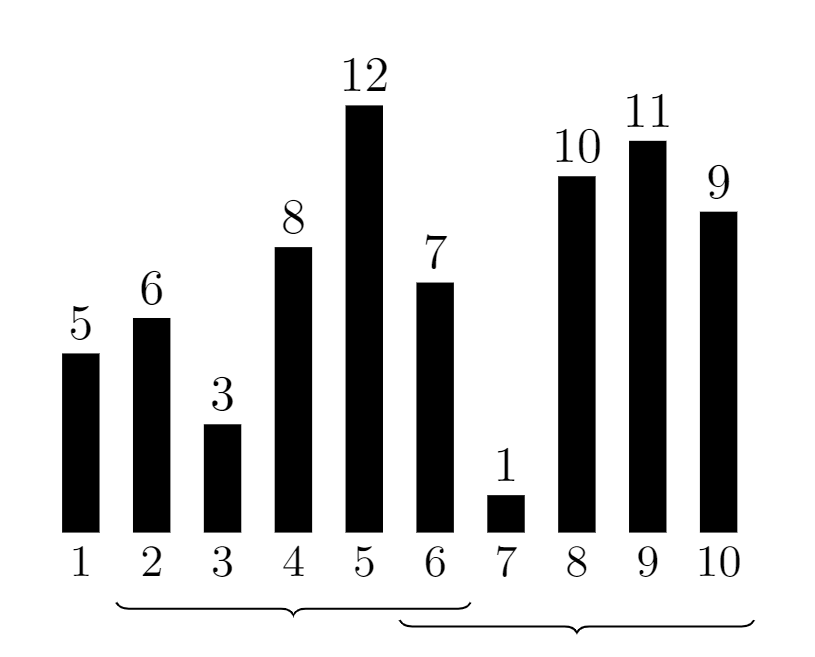
هر دو دنباله ی $6, 3, 8, 12, 7$ و $7, 1, 10, 11, 9$ با لوگوی نشان داده شده با جایگشت $(2, 1, 5, 3, 4)$ مچ میشن.
+ محدودیت زمان: ۲ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
نقشه شازززلند به شکل یه مستطیل $A×B$ است. که گوشه های مقابلش $(0 ,0)$ و $(A, B)$ ان.
شازززلند $n$ تا شهر داره که شهر $i$ ام در مختصات $ (x_i, y_i) $ قرار داره.
به شهر $i$ میگیم غربی اگر و تنها اگر $x_i = 0$
و بهش میگیم شرقی اگر و تنها اگر $x_i = A$
شهر ها به وسیله $m$ جاده به هم وصل شدن. جاده ها به شکل خط های مستقیم در نقشه از یک شهر به شهر دیگری هستند. جاده ها یا یک طرفه اند یا دو طرفه.
هیچ دو جاده ای همدیگه رو قطع نمی کنن. یعنی خط هاشون نقطه مشترک ندارن، مگر در شهر ها.
شهردار شازززلند نقشه شازززلند رو به شما داده و از شما میخواد به ازای هر شهر غربی پیدا کنید به چند شهر شرقی مسیر داره.
# ورودی
در خط اول ورودی اعداد $n$ و $m$ و $A$ و $B$ آمده اند.
$$1 \le n \le 300000$$$$0 \le m \le 900000$$$$1 \le A, B \le 10^9$$
در خط $i$ ام از $n$ خط بعدی $x_i$ و $y_i$ آمده اند.
$$0 \le x_i \le A$$$$0 \le y_i \le B$$
در خط i ام از m خط بعدی $c_i$ و $d_i$ و $k_i$ آمده اند.
$$1 \le c_i, d_i \le n$$$$1 \le k \le 2$$
اگر $k_i = 1$، جاده ای یک طرفه از شهر $c_i$ به شهر $d_i$ وجود دارد. در غیر این صورت، جاده ای دو طرفه بین شهر $c_i$ و $d_i$ وجود دارد. هیچ جاده ای بیشتر از یکبار در ورودی نیامده.
می تونید فرض کنید حداقل یه راس غربی وجود داره که به حداقل یه راس شرقی مسیر داره.
# خروجی
باید به ازای هر شهر غربی چاپ کنید به چند شهر شرقی مسیر دارد.
خروجی باید به ترتیب نزولی مختصات $y$ نقطه ها باشد.
یعنی برای بالاترین شهر غربی در خط اول خروجی
دومین بالا ترین شهر غربی در خط دوم خروجی و ...
# زیرمسئلهها
| زیرمسئله | نمره | محدودیت
|:------------------:|:----------:|:------------------:|
| ۱ | ۳۰ | $$ n, m \le 6000 $$ |
| ۲ | ۷۰ | بدون محدودیت اضافی |
# مثال
## ورودی نمونه ۱
```
5 3 1 3
0 0
0 1
0 2
1 0
1 1
1 4 1
1 5 2
3 5 2
```
## خروجی نمونه ۱
```
2
0
2
```
## ورودی نمونه ۲
```
12 13 7 9
0 1
0 3
2 2
5 2
7 1
7 4
7 6
7 7
3 5
0 5
0 9
3 9
1 3 2
3 2 1
3 4 1
4 5 1
5 6 1
9 3 1
9 4 1
9 7 1
9 12 2
10 9 1
11 12 1
12 8 1
12 10 1
```
## خروجی نمونه ۲
```
4
4
0
2
```
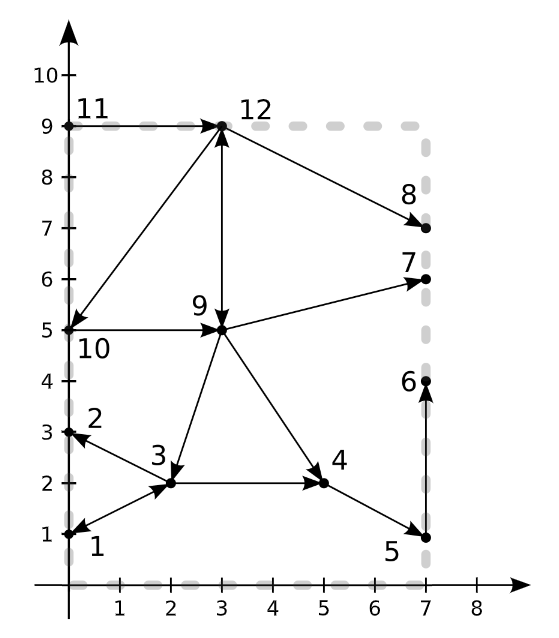
شهر در مختصات $ (0, 9)$ به $4$ شهر شرقی مسیر دارد.
شهر در مختصات $ (0, 5)$ به $4$ شهر شرقی مسیر دارد.
شهر در مختصات $ (0, 3)$ به $0$ شهر شرقی مسیر دارد.
شهر در مختصات $ (0, 1)$ به $2$ شهر شرقی مسیر دارد.