+ محدودیت زمان: ۲ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- اگر به رفتار استف‌های کدکاپ ۳ در طول مسابقه دقت کرده‌باشید، درمی‌یابید که *همه استفا عاشق مصطفی هستند*. در کدکاپ ۳ به هر کس ژتونی برای نهار داده شده که روی آن، رشته‌ای از حروف کوچک انگلیسی نوشته شده‌است. محمود که یکی از استف‌های زحمت‌کش مسابقات است عقیده دارد از بین همه استف‌های عاشق مصطفی، مصطفی خودش عاشق استفی است که رشته نوشته شده روی ژتونش بیشترین درجه تطابق و طول تطابق با رشته خودش را داشته باشد. از این رو او می‌خواهد درجه تطابق و طول تطابق رشته‌ خودش را با رشته مصطفی حساب کند. درجه تطابق و طول تطابق دو رشته به شکل زیر به دست می‌آید: رشته مصطفی را با $s$ و رشته محمود را با $t$ نشان می‌دهیم، طول هر دوی این رشته‌ها برابر $n$ است. فرض کنید یک گراف دو بخشی با $2n$ رأس داریم که رأس‌های بخش اول متناظر با کاراکترهای رشته‌ی $s$ و رأس‌های بخش دوم متناظر با کاراکترهای رشته‌ی $t$ است. به ازای هر دو اندیس $i$ و $j$ ($1 \le i, j \le n$) که کاراکتر $i$-ام از رشته‌ی $s$ و کاراکتر $j$-ام از رشته‌ی $t$ با یک‌دیگر برابر باشد یک یال بین رأس‌های متناظر این دو کاراکتر در گراف می‌گذاریم. طول تطابق رشته‌های $s$ و $t$ را برابر تعداد یال‌های **بزرگ‌ترین** تطابق در این گراف، و درجه تطابق رشته‌های $s$ و $t$ را برابر تعداد بزرگ‌ترین تطابق‌های این گراف می‌نامیم. یک تطابق در گراف یک زیرمجموعه از یال‌های آن گراف است که هیچ دو یالی از آن در رأسی مشترک نیستند. دو تطابق را متفاوت فرض می‌کنیم اگر مجموعه‌ی یال‌های آن‌ها متفاوت باشد. حال محمود با دادن رشته مصطفی و رشته خودش به شما، از شما می‌خواهد که طول تطابق و باقی‌مانده درجه تطابق رشته خودش با رشته مصطفی به $10^9 + 7$ را برای او بدست آورید. # ورودی در خط اول $s$، که رشته مصطفی است، و در خط دوم رشته $t$، که رشته محمود است، به شما داده می‌شود. دقت کنید که هر دو رشته‌ فقط از حروف کوچک انگلیسی تشکیل شده است. $$ 1 \le |s| , |t| \le 200\ 000$$ # خروجی در یک خط دو عدد جدا شده با فاصله از هم چاپ کنید که عدد اول طول تطابق دو رشته و عدد دوم باقی‌مانده درجه تطابق دو رشته به $10^9 + 7$ است. # مثال ## ورودی نمونه ۱ ``` salam szszs ``` ## خروجی نمونه ۱ ``` 1 3 ``` توضیح: در نمونه اول طول تطابق ۱ بوده (متناظر با رشته‌ `s`) و تعداد زیر دنباله‌های رشته محمود که با رشته مصطفی مطابق هستند و طولشان نیز یک می‌باشد برابر ۳ است. ## ورودی نمونه ۲ ``` mostafa estafah ``` ## خروجی نمونه ۲ ``` 5 2 ``` ## ورودی نمونه ۳ ``` ab ba ``` ## خروجی نمونه ۳ ``` 2 1 ```

+ محدودیت زمان: ۲ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- اگر به رفتار استف‌های کدکاپ ۳ در طول مسابقه دقت کرده‌باشید، درمی‌یابید که *همه استفا عاشق مصطفی هستند*. تیمور که یکی از استف‌های زحمت‌کش مسابقات است عقیده دارد که از بین همه استف‌های عاشق مصطفی، مصطفی خودش عاشق استفی است که بتواند معماهای سخت را حل کند. مصطفی معمایی طرح کرده و آن را برای همه استف‌ها فرستاده است تا آن را حل کنند. او جدولی $m \times n$ برای استف‌ها فرستاده که هر خانه از آن `x` یا `y` است. استف‌ها می‌توانند در هر مرحله یک خانه از جدول را انتخاب کنند و محتوای‌ درون آن خانه را به `x` ، ‍`y` یا ‍‍`z` تبدیل کنند. استفی که بتواند در کمترین مراحل کاری کند که شرایط زیر برقرار باشد، این معما را حل کرده است. ۱- مسیری از یکی از خانه‌های سطر اول به یکی از خانه‌های سطر آخر وجود داشته باشد که خانه‌های آن فقط `y` و ‍`z` باشد. ۲- مسیری از یکی از خانه‌های ستون اول به یکی از خانه‌های ستون آخر موجود باشد که خانه‌های آن فقط `x` و ‍`z` باشد. یک مسیر، دنباله‌ای از خانه‌های جدول است که در آن هر خانه به جز خانه آخر، با خانه بعدی‌اش مجاور ضلعی است. از آنجایی که تیمور حوصله‌ی این سوسول بازی‌ها را ندارد از شما خواسته تا به او کمک کنید تا نظر مصطفی را جلب کند. # ورودی در خط اول ابتدا عدد $n$ که تعداد سطر‌های جدول است و سپس عدد $m$ که تعداد ستون‌های جدول است به شما داده می‌شود. در هر یک از $n$ خط بعدی، یک رشته‌ به طول $m$ از حروف `x` و `y` داده شده است. $$ 1 \le n , m \le 1 \ 000$$ # خروجی در یک خط کمترین مراحل تغییر لازم برای برآورده کردن شرط‌های مصطفی را چاپ کنید. # مثال ## ورودی نمونه ۱ ``` 2 2 xy yx ``` ## خروجی نمونه ۱ ``` 2 ``` ## ورودی نمونه ۲ ``` 3 5 xyxyy yyyxy yyyyx ``` ## خروجی نمونه ۲ ``` 3 ```

+ محدودیت زمان: ۲ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- اگر به رفتار استف‌های کدکاپ ۳ در طول مسابقه دقت کرده‌باشید، درمی‌یابید که *همه استفا عاشق مصطفی هستند*. علاوه بر استف‌ها، بچه‌های تیم علمی هم عاشق مصطفی هستند. نگارنده‌ی این سوال نیز که یکی از عشاق مخلص مصطفی است هر چقدر سعی کرد نتوانست این سوال را به استف‌ها و مصطفی ربط دهد. در آخر مجبور شد این سوال را بدون هیچ حاشیه و داستانی برای شما بیان کند. دو دنباله از اعداد طبیعی با نام $a$ و $b$ به طول $n$ داریم که اعضای آن‌ها را به ترتیب با $a_i$ و $b_i$ نشان می‌دهیم. مقدار $f(a,b)$ برابر است با تعداد اعضای مجموعه‌ی $\{(a_i, b_i) | 0 \leq i \leq n \}$. علامت $(x, y)$ به معنای زوج مرتب است، و دو زوج مرتب متفاوت اند اگر و فقط اگر در مولفه اول یا در مولفه دوم متفاوت باشد. مثلا $(1, 2)$ با $(2, 1)$ متفاوت است. حال ما می‌خواهیم طوری ترتیب دنباله $b$ را تغییر دهیم که مقدار $f(a, b)$ بیشینه شود. این مقدار بیشینه چند است؟ # ورودی در خط اول $n$ که طول دنباله $a$ و $b$ است به شما داده می‌شود. در خط بعدی $n$ عدد جدا شده با فاصله که اعضای دنباله‌ی $a$ است به شما داده می‌شود. در خط بعدی $n$ عدد جدا شده با فاصله که اعضای دنباله‌ی $b$ است به شما داده می‌شود. $$ 1 \le n, a_i, b_i \le 200 \ 000 $$ # خروجی در یک خط مقدار بیشینه تابع $f(a, b)$ را چاپ کنید. # مثال ## ورودی نمونه ۱ ``` 5 3 2 2 2 3 1 1 5 2 2 ``` ## خروجی نمونه ۱ ``` 5 ``` ## ورودی نمونه ۲ ``` 5 1 2 1 2 1 4 2 4 2 4 ``` ## خروجی نمونه ۲ ``` 4 ```

+ محدودیت زمان: ۱ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- اگر به رفتار استف‌های کدکاپ ۳ در طول مسابقه دقت کرده‌باشید، درمی‌یابید که _همه استفا عاشق مصطفی هستند_. امیر روی میز سرور (که مصطفی پشت آن می‌نشیند) تکه کاغذی پیدا کرده است که روی آن یک رشته پرانتزگذاری معتبر به صورت رنگی نوشته شده است و هر حرف آن به رنگ خاصی است. او پی برد که یکی از استف‌ها با سلیقه‌ی خاصی پرانتزگذاری را به صورت رنگی برای بدست آوردن دل مصطفی نوشته است. او متوجه می‌شود که استف عاشق از سبک رنگ آمیزی کوبیسم استفاده کرده است. رشته پرانتزگذاری $s$ با طول $n$ را در نظر بگیرید. برای هر حرف $i$ ،$m_i$ را برابر با اندیس پرانتز باز یا بسته متناظر با حرف $i$ رشته در نظر بگیرید. از آنجا که این پرانتزگذاری معتبر است، مقدار $m_i$ به ازای هر $i$ وجود دارد. برای مثال اگر دنباله پرانتزگذاری ما `(())()` باشد، دنباله‌ی $m$ برابر با $\{4, 3, 2, 1, 6, 5\}$ خواهد بود. این رشته یک رنگ آمیزی کوبی است اگر ویژگی‌های زیر را داشته باشد: 1. هر حرف به یکی از رنگ‌های ۱ تا $k$ رنگ شده باشد. 2. رنگ حرف $i$ و رنگ حرف $m_i$ باید برابر باشد. 3. اگر $m_i \ne i-1$ رنگ حرف $i$ با $i-1$ متفاوت باشد. 4. اگر $m_i \ne i+1$ رنگ حرف $i$ با $i+1$ متفاوت باشد. امیر می‌خواهد تعداد رنگ‌آمیزی‌های کوبی متفاوت $s$ با $k$ رنگ را زیر آن تکه کاغذ بنویسد تا مصطفی را بیشتر حیرت‌زده کند! از آنجا که این عدد خیلی بزرگ‌ است، باقی‌مانده آن را بر $10^9 + 7$ برایش بدست بیاورید. # ورودی در سطر اول ورودی دو عدد $n$ و $k$ آمده است. سپس در سطر بعد رشته پرانتزگذاری $s$ آمده‌است. تضمین می‌شود $s$ یک پرانتزگذاری معتبر است. $$1 \le k \le n \le 200\ 000$$ $$|s| = n$$ # خروجی در تنها سطر خروجی باقی‌مانده تعداد روش‌های رنگ‌آمیزی کوبی $s$ با $k$ رنگ را بر $10^9+7$ چاپ کنید. # مثال ## ورودی نمونه ۱ ``` 4 2 (()) ``` ## خروجی نمونه ۱ ``` 2 ``` ## ورودی نمونه ۲ ``` 6 3 (())() ``` ## خروجی نمونه ۲ ``` 12 ```

+ محدودیت زمان: ۳ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- اگر به رفتار استف‌های کدکاپ ۳ در طول مسابقه دقت کرده‌باشید، درمی‌یابید که *همه استفا عاشق مصطفی هستند*. کشور کوئرا از $n$ شهر تشکیل شده است که این $n$ شهر با $n - 1$ جاده دوطرفه به هم متصل شده‌اند به طوری که از هر شهر می‌توان با طی کردن تعدادی جاده به شهر شماره ۱ رسید. شهر شماره ۱ پایتخت کشور کوئراست و هرساله مجموعه مسابقات کدکاپ در این شهر برگزار می‌شود. از آنجایی که کدکاپ بزرگترین رویداد کشور کوئراست طی بخشنامه‌ای از همه شهر‌ها خواسته شده که حداقل یک استف برای مسابقات به شهر شماره ۱ بفرستند. متاسفانه مسابقه کدکاپ با تعمیر جاده‌های کشور کوئرا توسط وزارت راه و ترابری، مصادف شده است و جاده‌ی شماره $i$ که دو شهر $x_i$ و $y_i$ را به هم وصل می‌کند از روز $l_i$ تا روز $r_i$ در درست تعمیر است و امکان عبور از آن وجود ندارد. (یعنی اگر در روز $k$‌ ام به شهر $x_i$ برسیم به طوری که $ l_i \le k \le r_i$، باید تا روز $r_i + 1$ صبر کنیم تا بتوانیم به شهر $y_i$ برویم) به دلیل پیشرفت فناوری‌های ترابری در کشور کوئرا مدت زمانی که طول می‌کشد تا از یک جاده عبور کنیم (به شرط باز بودن آن) به صفر ثانیه رسیده‌است. یعنی در طول سفر از یک شهر به شهر دیگر تنها چیزی‌ که باعث معطل شدن ما می‌شود بسته بودن جاده‌‌ها است. حال مصطفی می‌خواهد بداند به ازای هر شهر، استف‌هایی که آن شهر برای کدکاپ می‌فرستد روز چندم به محل برگزاری مسابقات یعنی شهر ۱ می‌رسند. از آنجایی که کار سرورهای کدکاپ هنوز تمام نشده مصطفی این مسئولیت خطیر را به شما می‌سپرد. دقت کنید که تمامی استف‌ها در ثانیه‌ صفر از مبدا خود به سمت شهر ۱ راه می‌افتند. # ورودی در یک خط عدد $n$ که تعداد شهرهای کشور کوئراست به شما داده می‌شود. در $n - 1$ خط بعدی، درهر خط ۴ عدد $x_i$ و $y_i$ و $l_i$ و $r_i$ به شما داده می‌شود که به این معناست که جاده $i$ ام شهر $x_i$ و $y_i$ را به هم وصل می‌کند و در زمان $l_i$ تا $r_i$ در دست تعمیر است. $$ 2 \le n \le 500 \ 000 $$ $$ 1 \le x_i , y_i \le n $$ $$ 0 \le l_i \le r_i \le 500 \ 000 $$ تضمین می‌شود که با جاده‌های داده شده، از همه‌ی شهرها می‌توان به شهر شماره ۱ رسید. # خروجی در $n$ خط به ازای هر شهر یک عدد چاپ کنید که نشان می‌دهد استف‌های آن شهر در روز چندم به شهر ۱ ام می‌رسند. # مثال ## ورودی نمونه ۱ ``` 2 1 2 1 2 ``` ## خروجی نمونه ۱ ``` 0 0 ``` ## ورودی نمونه ۲ ``` 3 1 2 3 4 2 3 0 2 ``` ## خروجی نمونه ۲ ``` 0 0 5 ```

+ محدودیت زمان: ۲ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- اگر به رفتار استف‌های کدکاپ ۳ در طول مسابقه دقت کرده باشید، درمی‌یابید که *همه استفا عاشق مصطفی هستند*. چند روز پیش تولّد مصطفی بود و به همین مناسبت استف‌ها برای او یک ربات به اسم کریم خریدند. کریم در یک زمین بازی مستطیلی به ابعاد $n \times m$ قرار می‌گیرد و یک دنباله از دستورات را دریافت می‌کند و طبق آن‌ها در زمین بازی حرکت می‌کند. دور زمین بازی دیوار کشیده شده است و بعضی از مربّع‌های $1 \times 1$ شامل مانع هستند؛ در صورتی که کریم به دیوار دور زمین یا یکی از این موانع برخورد کند، منفجر می‌شود و مصطفی ناراحت می‌شود. هر دستوری که کریم دریافت می‌کند، با یکی از حروف `D`(حرکت به سمت پایین)، `U`(حرکت به سمت بالا)، `R`(حرکت به سمت راست) یا `L`(حرکت به سمت چپ) نمایش داده می‌شود. بنابراین اگر کریم مجموعه‌ی دستورات `DDRUL` را دریافت کند، ابتدا به اندازه‌ی ۲ خانه (مربّع $1 \times 1$) به پایین می‌رود. سپس یک خانه به راست، یک خانه به بالا و در نهایت یک خانه به چپ می‌رود. مصطفی بسیار ریسک‌پذیر است؛ او به پیشنهاد تیم علمی مبنی بر انجام یک بازی بسیار خطرناک با کریم جواب مثبت داده! بازی سه مرحله دارد. در مرحله‌ی *اوّل*، تیم علمی یک دنباله از دستورات کریم را بیان می‌کنند. در مرحله‌ی *دوم* مصطفی باید کریم را در یکی از $n.m$ خانه‌ی زمین بازی که شامل مانع نیست، قرار دهد. در مرحله‌ی *سوم* نیز، تیم علمی می‌تواند ترتیب دستورات در دنباله‌ای که مشخّص کرده بود را عوض کند. مثلن اگر دنباله‌ی دستورات ابتدایی `RRDDLLUU` باشد، پس از آن که مصطفی کریم را در یکی از خانه‌های زمین بازی قرار داد، تیم علمی می‌تواند دنباله‌ی دستوراتش را به `URLDURLD` تغییر دهد. در مرحله‌ی بعد نیز دنباله‌ی دستورات جدید را به کریم می‌دهیم و کریم طبق آن دستورات شروع به حرکت می‌کند. اگر کریم منفجر شود، مصطفی می‌بازد و ناراحت می‌شود، و در غیر این صورت مصطفی برنده‌ی میدان خواهد شد! می‌دانیم به ازای برخی از دنباله‌های دستورات که تیم علمی در مرحله‌ی اوّل انتخاب می‌کند، مصطفی در مرحله‌ی دوم کریم را هر جای زمین بازی قرار دهد، در مرحله‌ی سوم تیم علمی می‌تواند جابه‌جایی‌های دستورات را طوری انجام دهد که مصطفی ببازد. در بین این دنباله‌های دستورات، طول کوتاه‌ترین دنباله را بیابید. # ورودی در خط اول دو عدد $n$ و $m$ ابعاد جدول به شما داده می‌شود. در هر یک از $n$ خط بعدی، $m$ کاراکتر داده می‌شود. چنان‌چه خانه‌ی $j$ام در سطر $i$ام زمین بازی شامل مانع باشد، کاراکتر $j$امِ خط $i$ام برابر `#` و در غیر این صورت برابر `.` خواهد بود. $$ 1 \le n, m \le 2 \ 000 $$ # خروجی در یک خط طول کوتاه‌ترین دنباله‌ی ممکن با شرایط گفته شده را چاپ کنید. # مثال ## ورودی نمونه ۱ ``` 3 3 ... ... .## ``` ## خروجی نمونه ۱ ``` 3 ``` به طور مثال دنباله‌ی دستورات `RUU` برای این مثال مطلوب است. ## ورودی نمونه ۲ ``` 3 4 #### .### .#.. ``` ## خروجی نمونه ۲ ``` 2 ```

+ محدودیت زمان: ۲ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- اگر به رفتار استف‌های کدکاپ ۳ در طول مسابقه دقت کرده‌باشید، درمی‌یابید که *همه استفا عاشق مصطفی هستند*. شایعه شده‌است که او از یکی از استف‌ها خوشش میاید و اسم او را در دفترچه یادداشت دیجیتالش نوشته‌است! هر کسی در زندگی‌اش رمزهایی دارد، مصطفی نیز دفترچه‌اش بی‌رمز نیست و رمزی طولانی دارد! ساعت ۴ صبح دیروز، مصطفی که بعد از آماده‌سازی‌های کدکاپ خیلی خسته بود، حواسش نبود و کلید اسرارش را فاش کرد! او به جواد که کنار او نشسته بود جدولی نشان می‌دهد (شکل زیر) و می‌گوید که ۴ دنباله $a$، $b$، $c$ و $d$ به طول $n$ دارد که دنباله‌های $c$ و $d$ تنها از ۰ و ۱ تشکیل شده‌اند. او از این دنباله جدولی $n \times n$ می‌سازد که در خانه‌ی واقع در سطر $i$ و ستون $j$ عدد $a_i \times b_j \times (c_i \oplus d_j)$ قرار دارد ($\oplus$ نماد عملگر *XOR* است). سپس به جواد می‌گوید که رمز دفترچه یادداشت دیجیتالش جمع اعداد زیرجدولی $k \times k$ است که جمع اعدادش بیشینه است!  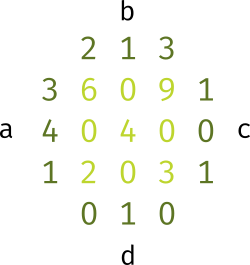اکنون مصطفی از فرط خستگی خوابش برده‌است. جواد موفق شده‌است ۴ دنباله $a$، $b$، $c$ و $d$ را بیابد. حال شما باید رمز دفترچه یادداشت دیجیتال مصطفی را بیابید. # ورودی سطر اول ورودی شامل دو عدد $n$ و $k$ است. سپس در سطر دوم دنباله $a_1, ..., a_n$ شامل $n$ عدد آمده‌است. سپس به همین شکل در سطر سوم دنباله $b$ و در سطر چهارم دنباله $c$ و در سطر پنجم دنباله $d$ آمده‌است. همه اعداد ورودی اعدادی صحیح هستند. $$2 \le k \le n \le 200\ 000$$ $$0 \le a_i, b_i \le 1\ 000$$ $$0 \le c_i, d_i \le 1$$ # خروجی در تنها سطر خروجی رمز دفترچه یادداشت دیجیتال مصطفی را چاپ کنید. # مثال ## ورودی نمونه ``` 3 2 3 4 1 2 1 3 1 0 1 0 1 0 ``` ## خروجی نمونه ``` 13 ```