+ محدودیت زمان: ۰.۵ ثانیه
+ محدودیت حافظه: ۶۴ مگابایت
----------
علی عاشق کدکاپ شده و نمیخواهد بپذیرد که هر مسابقهای یک پایانی دارد! به همین دلیل میخواهد رشته بیپایان $s$ را در کدکاپ ۶ بهعنوان یادگاری باقی بگذارد.

رشته $s$ یک رشته (از سمت راست) نامتناهی است که از نامتناهی بار اضافه کردن `codecup6` به سمت راست یک رشته خالی بدست میآید:
کاراکتر اول این رشته یعنی $s_1$ برابر `c`، کاراکتر دوم این رشته یعنی $s_2$ برابر `o`، کاراکتر سوم این رشته یعنی $s_3$ برابر `d` و... است.
امین که رابطه خوبی با نامتناهیها ندارد عدد صحیح و مثبت $n$ را به علی میدهد و مقدار $s_n$ را از او میپرسد. به علی کمک کنید تا به سوال امین پاسخ دهد.
# ورودی
ورودی تنها شامل یک سطر است و در آن عدد صحیح و مثبت $n$ آمده است.
$$1 \le n \le 100$$
# خروجی
در تنها سطر خروجی مقدار $s_n$ که تنها یک کاراکتر است را چاپ کنید.
**توجه کنید سیستم داوری به کوچکی و بزرگی حروف حساس است.**
# مثال
## ورودی نمونه ۱
```
1
```
## خروجی نمونه ۱
```
c
```
<details class="green">
<summary>
**توضیح نمونه ۱.**
مقدار $s_1$ برابر `c` است.
</summary>
```
<mark class="violet">c</mark>odecup6codecup6codecup6...
```
</details>
## ورودی نمونه ۲
```
2
```
## خروجی نمونه ۲
```
o
```
<details class="green">
<summary>
**توضیح نمونه ۲.**
مقدار $s_2$ برابر `o` است.
</summary>
```
c<mark class="violet">o</mark>decup6codecup6codecup6...
```
</details>
## ورودی نمونه ۳
```
8
```
## خروجی نمونه ۳
```
6
```
<details class="green">
<summary>
**توضیح نمونه ۳.**
مقدار $s_8$ برابر `6` است.
</summary>
```
codecup<mark class="violet">6</mark>codecup6codecup6...
```
</details>
## ورودی نمونه ۴
```
9
```
## خروجی نمونه ۴
```
c
```
<details class="green">
<summary>
**توضیح نمونه ۴.**
مقدار $s_9$ برابر `c` است.
</summary>
```
codecup6<mark class="violet">c</mark>odecup6codecup6...
```
</details>
تکرار کدکاپی
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
دیروز $n$ دوست باهم به رستوران رفتهاند، آنها خیلی صمیمی هستند و غذاهایی که سفارش میدهند باهم به اشتراک میگذارند پس موقع حساب و کتاب هم خرجهایشان را **یکسان** بین خودشان تقسیم میکنند.
برای اینکه این حساب و کتابشان را راحت انجام دهند همیشه یکی از این افراد **«مادرخرج»** میشود؛ یعنی کل هزینهها را به رستوران میدهد و فردای آن روز $n - 1$ نفر دیگر خرج آن روز را برای «مادرخرج» واریز میکنند.
اگر فرض کنید کل خرج رستوران $S$ تومان باشد. سهم هر کس دقیقاً $\frac{S}{n}$ تومان میشود. پس باید هرکس به جز «مادرخرج» مبلغ $\frac{S}{n}$ به حساب «مادرخرج» واریز کند تا حسابها درست شود.
اما میدانیم انجام یک واریز و انتقال پول هزینهای برای **ارسال کننده** دارد. در این سوال فرض کنید $a$ تومان از حساب واریزکننده بابت کارمزد این واریز کسر خواهد شد.

این موضوع باعث میشود که «مادرخرج» در مجموع هزینه کمتری را پرداخت کند! (چون $a$ تومان کمتر از بقیه پرداخت کرده است.)
از شما میخواهیم بگویید هر کس (به جز «مادرخرج») چقدر به حساب «مادرخرج» واریز کند تا پول خرج شده توسط همه این $n$ نفر یکسان باشد و یا بگویید انجام چنین کاری امکان پذیر نیست. (فرض کنید همه این $n$ نفر به اندازه کافی پول در حسابهایشان دارند.)
توجه کنید هرکس به جز «مادرخارج» **دقیقاً یک انتقال پول با مبلغی صحیح و مثبت** به حساب «مادرخرج» انجام میدهد و هیچ انتقال پول دیگری بین حساب این $n$ نفر مجاز نیست.
همچنین توجه کنید خرج رستوران که توسط «مادرخرج» پرداخت شده هیچ کارمزدی از حساب او کم نمیکند بلکه انتقال بین حساب است که کارمزد دارد.
برای بهتر متوجه شدن خواسته سوال توضیحات نمونه را مطالعه کنید.
# ورودی
در سطر اول ورودی عدد $t$ داده میشود. این عدد نشاندهنده تعداد نمونههایی است که باید پاسخ آنها را چاپ کنید.
$$1 \le t \le 100$$
سپس در $t$ سطر بعدی در هر سطر سه عدد صحیح و مثبت $n$ و $S$ و $a$ داده میشود که به ترتیب نشاندهنده تعداد افراد، مجموع هزینههای رستوران و هزینه انجام یک تراکنش برای ارسال کننده است.
$$2 \le n \le 100 \quad \quad 1 \le a \le 1000 \quad \quad 1 \le S \le 100 \ 000$$
**توجه کنید این $t$ نمونه هیچ ارتباطی به هم ندارند و هر کدام مسئلهای مستقل هستند.**
# خروجی
خروجی شامل $t$ سطر است و در هر سطر پاسخ یک نمونه چاپ میشود. درصورتی که عدد **صحیح و مثبتی** مثل $x$ وجود دارد که اگر هرکس به جز «مادرخرج»، $x$ تومان برای مادرخرج واریز کند، مقدار پول کسر شده از حساب همه یکسان خواهد بود، مقدار $x$ و اگر چنین عدد صحیحی وجود ندارد `-1` را چاپ کنید.
# مثال
## ورودی نمونه
```
5
3 2000 5
2 201 1
5 30 1
2 100 100
3 3 100
```
## خروجی نمونه
```
665
100
-1
-1
-1
```
<details class="green">
<summary>
**توضیح نمونه اول**
</summary>
ابتدا از حساب «مادرخرج» ۲۰۰۰ تومان کسر شدهاست، سپس توسط دو نفر دیگر هر کدام ۶۶۵ تومان به حساب مادرخرج واریز شده است. پس در مجموع کل مبلغ پرداخت شده توسط «مادرخرج» برابر است با:
$$2000 - 2 \times 665 = 670$$
بقیه افراد هر کدام نفری ۶۶۵ تومان به حساب «مادرخرج» واریز میکنند و ۵ تومان هم کارمزد این واریز را پرداخت میکنند پس مجموع پرداختی این افراد برابر است با:
$$665 + 5 = 670$$
و این عادلانه است چون در مجموع از حساب همه افراد، ۶۷۰ تومان کسر شدهاست.
</details>
<details class="green">
<summary>
**توضیح نمونه دوم**
</summary>
ابتدا از حساب «مادرخرج» ۲۰۱ تومان کسر شدهاست، سپس توسط فرد دیگر ۱۰۰ تومان به حساب «مادرخرج» واریز شدهاست. پس در مجموع کل مبلغ پرداخت شده توسط «مادرخرج» برابر است با:
$$201 - 100 = 101$$
فرد دیگر ۱۰۰ تومان به حساب «مادرخرج» واریز میکند و ۱ تومان هم کارمزد این واریز را پرداخت میکند پس مجموع پرداختی این فرد برابر است با:
$$100 + 1 = 101$$
و این عادلانه است چون در مجموع از حساب همه افراد، ۱۰۱ تومان کسر شدهاست.
</details>
<details class="green">
<summary>
**توضیح نمونه سوم**
</summary>
هیچ مبلغ **صحیح و مثبتی** نمیتوان برای انجام تراکنش انتخاب کرد.
ابتدا از حساب «مادرخرج» ۳۰ تومان کسر شده است. اگر هر فرد به جز مادر خرج مبلغ ۶ تومان به حساب «مادرخرج» واریز کند. مجموع کل مبلغ پرداخت شده توسط مادر خرج برابر است با:
$$30 - 4 \times 6 = 6$$
بقیه افراد هر کدام نفری ۶ تومان به حساب «مادرخرج» واریز میکنند و ۱ تومان هم کارمزد این واریز را پرداخت میکنند پس مجموع پرداختی این افراد برابر است با:
$$6 + 1 = 7$$
و این عادلانه نیست چون در مجموع از حساب مادر خرج ۶ تومان کسر شده ولی از حساب بقیه ۷ تومان کسر میشود.
با استدلالهای مشابه میتوانید نتیجه بگیرید که هیچ **عدد صحیح و مثبتی** برای تسویه حساب به صورت عادلانه وجود ندارد. پس به جای پاسخ مسئله `-1` چاپ میکنیم.
</details>
<details class="green">
<summary>
**توضیح نمونه چهارم**
</summary>
اگر فرد به غیر از «مادرخرج» هر مبلغ **صحیح و مثبتی** به حساب «مادرخرج» واریز کند مجموع پول کسر شده از حساب مادرخرج کمتر از ۱۰۰ تومان و فرد دیگر بیشتر از ۱۰۰ تومان خواهد بود. پس هیچ روشی برای تسویه حساب عادلانه وجود ندارد. پس به جای پاسخ مسئله `-1` چاپ میکنیم.
</details>
<details class="green">
<summary>
**توضیح نمونه پنجم**
</summary>
در این نمونه هزینه کارمزد انتقال زیاد است و چون انتقال با مبلغ منفی نداریم (!) هیچ روشی برای تسویه حساب عادلانه نداریم. پس به جای پاسخ مسئله برابر `-1` چاپ میکنیم.
</details>
دَنگ و دُنگ
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
علی در شهری نامتناهی زندگی میکند که خیابانهای آن مانند شکل زیر است. شما میتوانید خانه علی که در یکی از تقاطعهای این شهر قرار دارد را در تصویر زیر ببیند.

علی در خانه مانده و حوصلهاش خیلی سررفته و میخواهد در شهر گشتی بزند. گشت زدن علی $n$ مرحله دارد. علی در هر مرحله یکی از ۶ جهت که با حروف $\{ A, B, C, D, E, F \}$ در شکل نشاندادهایم را انتخاب میکند و از محل تقاطع فعلی در آن جهت حرکت میکند تا به تقاطع بعدی برسد.
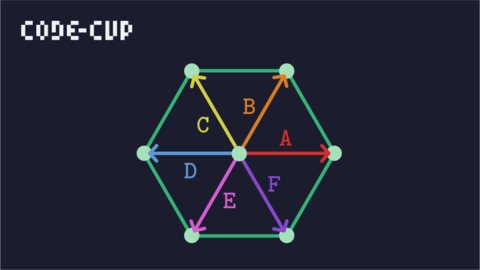
پس یک گشت علی را میتوان به صورت یک رشته به طول $n$ مثل:$$s_1, s_2, s_3, \dots, s_n$$
نشان داد به طوری که برای هر $i$ از ۱ تا $n$:
$$s_i \in \{A, B, C, D, E, F\}$$
علی میخواهد برای هر یک از $t$ گشتی که انتخاب کرده است، فاصلهی نقطهی پایانی این گشت را با خانه حساب کند.
منظور از فاصله دو تقاطع، یعنی طول کوتاهترین گشتی که بتوان با کمک آن از یک تقاطع به تقاطع دیگر رفت. همچنین فاصله دو تقاطع یکسان را ۰ در نظر میگیریم.
# ورودی
در سطر اول ورودی عدد صحیح و مثبت $t$ آمده است. که نشاندهندهی تعداد گشتهایی است که در این ورودی آمده است.
$$1 \le t \le 1 \, 00 \, 000$$
در $t$ سطر بعدی، در هر سطر یک رشته که تنها شامل حروف $\{ A, B, C, D, E, F \}$ است آمده که نشاندهنده یک گشت علی است.
تضمین میشود مجموع طول رشتهها در یک ورودی از ۱۰۰,۰۰۰ بیشتر نشود.
# خروجی
خروجی شامل $t$ سطر است که در هر سطر یک عدد صحیح و نامنفی، که نشاندهنده فاصله تقاطع نهایی علی بعد از انجام آن گشت تا تقاطعی که خانه علی در آن قرار دارد است.
# مثال
## ورودی نمونه
```
3
A
AB
ABC
```
## خروجی نمونه
```
1
2
2
```
**شکل حرکت علی در گشت اول.**
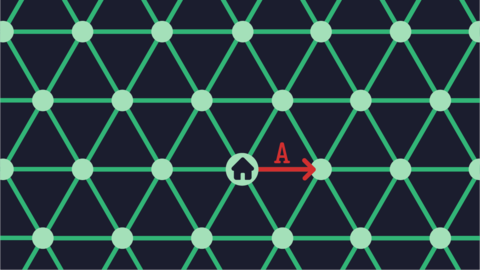
**شکل حرکت علی در گشت دوم.**
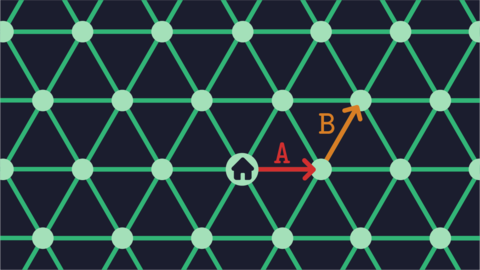
**شکل حرکت علی در گشت سوم.**
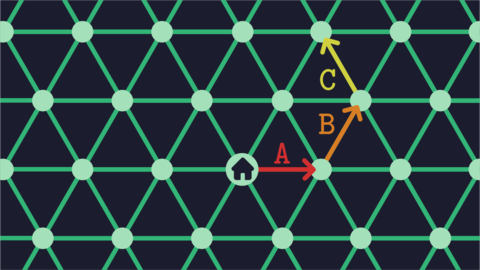
هگزانوردی
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
یک دنباله از اعداد صحیح $a_1, a_2, a_3, \dots, a_n \,$ و دو عدد صحیح و مثبت $k$ و $m$ داریم ($1 \le k \le n \,$) و از روی آن دنباله $b$ را میسازیم.
ابتدا دنباله $b$ خالی است و بهعنوان اولین عنصر این دنباله $a_k$ را در آن قرار میدهیم. سپس تا زمانی که تعداد اعداد موجود در دنباله $b$ برابر $m$ نشده است، اگر سمت راست ترین عددی که به دنباله $b$ اضافه کردیم برابر $a_i$ بوده است عدد $a_{i \% n + 1}$ را به سمت راست دنباله $b$ اضافه میکنیم.
برای مثال فرض کنید دنباله $a$ برابر
$$1, 12, 7, -4$$
و $m = 9$ و $k = 3$ باشد، دنباله $b$ در نهایت برابر
$$b = 7, -4, 1, 12, 7, -4, 1, 12, 7$$
خواهد بود.
حال دنباله $a$ و مقدار $k$ گمشده است و فقط مقدار $m$ و دنباله نهایی $b$ را داریم. از شما میخواهیم **کمترین طول ممکن** برای دنباله $a$ که بشود با انتخاب یک $k$ مناسب به این دنباله $b$ رسید را بیاید و دنباله $a$ را پیدا کنید.
اگر چند دنباله با کمترین طول وجود دارد یکی از جوابها را به دلخواه چاپ کنید.
# ورودی
در سطر اول ورودی عدد صحیح و مثبت $t$ آمده که تعداد تستهای نمونهای که به شما داده میشود را نشان میدهد. سپس برای هر تست در یک سطر عدد صحیح $m$، در سطر بعدی $m$ عدد صحیح $b_1, b_2, b_3, \dots, b_m \,$ که با فاصله از هم جدا شدهاند، آمده است.
$$1 \le m \le 100\,000$$
$$|b_i| \le 10^9$$
تضمین میشود مجموع $m$ برای همه دنبالههایی که در این $t$ تست به شما داده میشود از ۱۰۰,۰۰۰ بیشتر نمیشود.
# خروجی
برای هر کدام از این $t$ تست در یک سطر کمترین طول ممکن برای دنباله $a$ و در سطر بعدی دنباله $a$ای با همان طول که اعضای آن با فاصله جدا شده است را چاپ کنید.
اگر چندین جواب برای یک مسئله وجود دارد یکی را به دلخواه چاپ کنید.
# مثال
## ورودی نمونه
```
3
9
7 -4 1 12 7 -4 1 12 7
6
3 1 2 3 1 2
5
1 2 3 4 5
```
## خروجی نمونه
```
4
1 12 7 -4
3
1 2 3
5
1 2 3 4 5
```
**توضیح نمونه اول.**
توضیح این نمونه در متن سوال آمده است.
**توضیح نمونه دوم.**
کافی است دنباله $a$ را به صورت $<1, 2, 3>$ و مقدار $k = 3$ باشد تا دنباله ورودی داده شده ساخته شود.
**توضیح نمونه سوم.**
کافی است دنباله $a$ را به صورت $<1, 2, 3, 4, 5>$ و مقدار $k = 1$ باشد تا دنباله ورودی داده شده ساخته شود.
دنباله گمشده
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
مارچلو که از سپری کردن تابستان خود در یک مسافرت رویایی داشت نهایت لذت را میبرد، تصمیم گرفت که ورزشی را به طور حرفهای شروع کند و چه ورزشی بهتر از پرش با دنباله!
مارچلو دو دنبالهی $n$ تایی از اعداد صحیح دارد که عضو $i$اُم دو دنباله را به ترتیب با $a_i$ و $b_i$ نشان میدهیم. او میخواهد ابتدا دنبالهی پرشهای خود را بدست بیاورد و سپس اقدام به پرش کند.
دنبالهی $<d_{1},\,d_{2},\,...,\,d_{k}>$ را یک **دنبالهی پرش** میگوییم، اگر:
+ $k \le n$
+ $1 \le d_i \le n$
+ $\forall_{i<j}\,d_{i}\neq d_{j}$
به دنبالهی پرش $<d_{1},\,d_{2},\,...,\,d_{k}>$ یک **دنبالهی پرش معتبر** میگوییم، اگر:
+ $a_{d_i} \le a_{d_{i+1}}$
+ $\left|a_{d_{i}}-a_{d_{i+1}}\right|\leq\left|b_{d_{i}}-b_{d_{i+1}}\right|$
مارچلو که سخت عزم خود را برای حرفهای شدن در این ورزش جزم کرده بود، از شما میخواهد که بلندترین دنبالهی پرش معتبر در دو دنبالهی داده شده را به او گزارش دهید، تا طبق آن پرشهای خود را انجام دهد.
# ورودی
ورودی شامل سه خط است که در خط اول، عدد طبیعی $n$ آمده است و در خط دوم $n$ عدد با فاصله از هم آمده است که عدد $i$اُم نشاندهندهی $a_i$ است. در خط سوم نیز $n$ عدد با فاصله از هم آمده است که عدد $i$اُم، نشاندهندهی $b_i$ است.
$$1 \le n \le 100\ 000$$
$$1 \le a_i, b_i \le 100\ 000$$
**تضمین میشود $a_i$ها متمایز هستند.**
# خروجی
در تنها خط خروجی، طول بلندترین دنبالهی پرش معتبر را چاپ کنید.
## ورودی نمونه ۱
```
3
2 1 3
4 5 9
```
## خروجی نمونه ۱
```
3
```
دنبالهی $<2,\,1,\,3>$ بلندترین دنبالهی پرش معتبر است.
## ورودی نمونه ۲
```
5
5 1 6 2 3
9 3 1 4 4
```
## خروجی نمونه ۲
```
4
```
دنبالهی $<2,\,4,\,1,\,3>$ بلندترین دنبالهی پرش معتبر است.
پرش با دنباله
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
امین میخواهد در یک امتحان شرکت کند او $n$ کلمه مختلف را باید حفظ کند این کلمات همگی به طول $k$ هستند. امین که آدم تنبلی است به جای حفظ کردن این کلمات تصمیم به یادداشت کردن آنها و تقلب دارد.
امین برای تقلب سبک خودش را دارد. او میخواهد $n$ کاراکتر دور یک دایره بنویسید به طوری که همهی $n$ کلمهای که باید حفظ میکرد را بتوان با شروع از یکی از این $n$ کاراکتر و حرکت در جهت ساعتگرد و یادداشت کردن $k$ کارکتر پشت هم به دست آورد.
توجه کنید ترتیب ظاهر شدن کلمهها دور دایره اهمیتی ندارد و میتوانند به هر ترتیبی ظاهر شوند اما این $n$ کلمه لزوماً متمایز نیستند و اگر یک کلمه $m$ بار در ورودی ظاهر شود باید دور دایره نیز دقیقاً $m$ بار دیده شود.
به امین کمک کنید تا این ترتیب از کاراکتر را بدست آورد. اگر چند ترتیب وجود دارد یکی از آنها را به دلخواه چاپ کنید. همچنین اگر انجام چنین کاری ممکن نیست این خبر بد را با چاپ کردن `-1` مشخص کنید.
# ورودی
در خط اول ورودی به شما دو عدد صحیح $n$ و $k$ داده میشود. در $n$ خط بعدی هر کدام یک رشته به طول $k$ داده میشود. همگی این رشته ها از حروف کوچک انگلیسی تشکیل شدهاند.
$$ 1 \le n \times k \le 500 \, 000$$
# خروجی
در تنها سطر خروجی یک رشته به طول $n$ که پاسخ مسئله است را چاپ کنید. ترتیب رشته از چپ به راست ساعتگرد است. اگر پاسخی برای مسئله وجود ندارد در تنها سطر خروجی `-1` را چاپ کنید.
# مثال
## ورودی نمونه ۱
```
3 3
abc
bca
cab
```
## خروجی نمونه ۱
```
abc
```
## ورودی نمونه ۲
```
4 2
aa
ab
ba
bb
```
## خروجی نمونه ۲
```
aabb
```
حروف چینی
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
گراف $G$ یک گراف ساده و بدون جهت است. $G$ شامل $n$ راس و $m$ یال است. فرض کنید یالهای $G$ به ترتیب ورودی مسئله
$$e_1, e_2, e_3, \dots, e_m$$
باشند.
از شما میخواهیم برای $q$ بازه $l_i$ و $r_i$ بررسی کنید آیا اجتماع یالهای این بازه تشکیل یک زیردرخت برای $G$ میدهد یا نه. به عبارت دیگر اجتماع
$$e_{l_i}, e_{l_i + 1}, e_{l_i + 2}, \dots, e_{r_i}$$
تشکیل یک زیردرخت برای $G$ میدهد یا نه.
توجه کنید یک زیردرخت از $G$ یک زیرمجموعه از یالهای $G$ است که تشکیل یک گراف همبند بدون دور را بدهد. (نیازی نیست که این زیردرخت فراگیر باشد و شامل همه راسهای $G$ باشد.)
# ورودی
در سطر اول ورودی دو عدد صحیح و مثبت $n$ و $m$ با یک فاصله آمده است که به ترتیب نشاندهنده تعداد راسها و تعداد یالهای گراف است.
$$2 \le n \le 100 \, 000 \quad\quad 1 \le m \le 100 \, 000$$
در $m$ سطر بعدی در هر سطر دو عدد صحیح و مثبت $u_i$ و $v_i$ با یک فاصله آمده است که نشاندهندهی یال $i$ام گراف یعنی $e_i$ است.
$$1 \le u_i \neq v_i \le n$$
تضمین میشود هیچ یالی دوبار ورودی داده نمیشود و گراف داده شده در ورودی یک گراف ساده (نه لزوماً همبند) خواهد بود.
در سطر بعدی تنها یک عدد صحیح و مثبت $q$ آمده است که تعداد سوالاتی را نشان میدهد.
$$1 \le q \le 100 \, 000$$
در $q$ سطر بعدی در هر سطر دو عدد صحیح و مثبت $l_i$ و $r_i$ آمده است که بازه مورد نظر در سوال $i$ام را نشان میدهد.
$$1 \le l_i \le r_i \le m$$
# خروجی
خروجی شامل $q$ سطر است و در سطر $i$ام آن اگر زیرگراف متناظر با بازهی $i$ام مورد سوال، درخت بود کلمه `YES` و در غیر این صورت کلمه `NO` را چاپ کنید.
# مثال
## ورودی نمونه ۱
```
3 3
1 2
1 3
2 3
6
1 1
1 2
1 3
2 2
2 3
3 3
```
## خروجی نمونه ۱
```
YES
YES
NO
YES
YES
YES
```
## ورودی نمونه ۲
```
5 5
1 2
3 4
2 3
4 5
5 1
4
1 2
1 3
1 4
1 5
```
## خروجی نمونه ۲
```
NO
YES
YES
NO
```