+ محدودیت زمان: ۰.۵ ثانیه
+ محدودیت حافظه: ۶۴ مگابایت
----------
*امروز روز جهانیه ریاضیاته! و «هندسه» یکی از مباحث قدیمی اونه...*

%align_center_start%
*دکتر سیاوش شهشهانی*
%align_end%
امیرحسام دو تکه چوب با طولهای $a$ و $b$ دارد. او میخواهد **دقیقاً یکبار** یکی از این دو تکه چوب را بردارد و به دو تکه چوب با طولهای **حقیقی و مثبت** (نه لزوماً برابر) تقسیم کند.
منظور از تقسیم کردن یک چوب با طول $l$ یعنی آن را به دو چوب با طولهای مثبت $y$ و $l - y$ تبدیل کنیم.
او میخواهد طوری این تقسیم را انجام دهد به طوری که بتوانیم با سه تکه چوب جدید، اضلاع مثلثی با مساحت ناصفر بسازیم. بررسی کنید آیا امیرحسام میتواند چنین کاری را انجام دهد یا نه.
با سه تکه چوب با طولهای حقیقی و مثبت $x$، $y$ و $z$ میتوان یک مثلث با مساحت ناصفر ساخت اگر و تنها اگر
$$x + y > z, \quad x + z > y, \quad y + z > x$$
# ورودی
در سطر اول ورودی دو عدد صحیح و مثبت $a$ و $b$ که با یک فاصله از هم آمدهاند و نشاندهنده طول چوبها است.
$$1 \le a, b \le 100$$
# خروجی
در تنها سطر خروجی، در صورتی که انجام این کار شدنی است؛ کلمه `YES` و در غیر این صورت `NO` را چاپ کنید.
**توجه کنید سیستم داوری به بزرگی و کوچکی حروف حساس است.**
# مثالها
## ورودی نمونه ۱
```
2 3
```
## خروجی نمونه ۱
```
YES
```
انجام این کار ممکن است، چوب دوم با طول ۳ را به دو قسمت با طول ۱ و ۲ تقسیم میکنیم. در این صورت طول این تکه چوبها ۲، ۲، ۱ خواهد بود که میتوان با آنها مثلث ساخت.
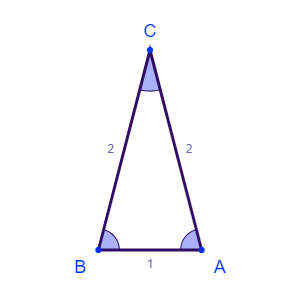
توجه کنید این روش تقسیم یکتا نیست برای مثال میتوان چوب با طول ۳ را به دو قسمت با طول ۱.۵ و ۱.۵ تقسیم کنیم و با سه تکه چوب با طولهای ۱.۵، ۱.۵ و ۲ میتوان مثلث ساخت.
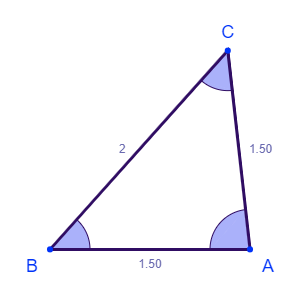
## ورودی نمونه ۲
```
2 2
```
## خروجی نمونه ۲
```
NO
```
هیچ روشی برای تقسیم کردن یک چوب و ساختن یک مثلث با مساحت ناصفر با اضلاع این سه چوب وجود ندارد.
دو تکه چوب
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۶۴ مگابایت
----------
*امروز روز جهانیه ریاضیاته! و «آنالیز حقیقی» یکی از مباحث هیجان انگیز و دوست داشتنی اونه...*

%align_center_start%
*دکتر مریم میرزاخانی*
%align_end%
منظور از بازه $[a, b]$ (بخوانید بازه **بسته** $a$ و $b$) یعنی مجموعه تمام نقاط بین $a$ و $b$ (شامل $a$ و $b$) به عبارت دیگر یعنی:
$$[a, b] = \{ x \in \mathbb{R} | a \leq x \leq b \}$$
منظور از بازه $(a, b)$ (بخوانید بازه **باز** $a$ و $b$) مجموعه تمام نقاط بین $a$ و $b$ (بدون $a$ و $b$) به عبارت دیگر یعنی:
$$(a, b) = \{ x \in \mathbb{R} | a < x < b \}$$
محسن همه **اعداد حقیقی** بازه بسته $[1, 100]$ را یادداشت کرده است.
محسن $n$ بازه $[l_i, r_i]$ که ($1 \leq l_i \leq r_i \leq 100\,$) در مجموعه اعداد خود را دوست دارد و اگر عددی از آن حذف شود، محسن ناراحت میشود. توجه کنید ممکن است این بازهها اشتراک داشتهباشند.
محسن در هر عملیات میتواند یک بازه باز مثل $(x, y)$ که ($1 \leq x < y \leq 100$) را انتخاب کند و همهی نقاط باقیمانده از مجموعه محسن را که در این بازه قرار دارد؛ از مجموعه محسن حذف کند.
محسن میخواهد با **کمترین** تعداد عملیات کاری کند که فقط بازههای مورد علاقه محسن در مجموعه او باقیبماند. (برای بهتر متوجه شدن سوال مثالها را مطالعه کنید.)
به محسن کمک کنید تا کمینه تعداد عملیات لازم را محاسبه کند. اگر انجام این کار با تعداد متناهی عملیات شدنی نیست این خبر بد را به محسن بگویید.
# ورودی
در سطر اول ورودی عدد صحیح و مثبت $n$ آمده است که تعداد بازهها را نشان میدهد.
$$1 \leq n \leq 100$$
در $n$ سطر بعدی در سطر$i$ دو عدد صحیح $l_i$ و $r_i$ آمده است.
$$1 \leq l_i \leq r_i \leq 100$$
# خروجی
در صورتی که با انجام عملیات فوق این کار شدنی است، کمینه تعداد عملیات لازم را چاپ کنید. در غیر این صورت `-1` را چاپ کنید.
# مثالها
## ورودی نمونه ۱
```
5
1 30
90 100
10 60
75 75
70 80
```
## خروجی نمونه ۱
```
2
```
کافی است بازه $(60, 70)$ و بازه $(80, 90)$ حذف شود.
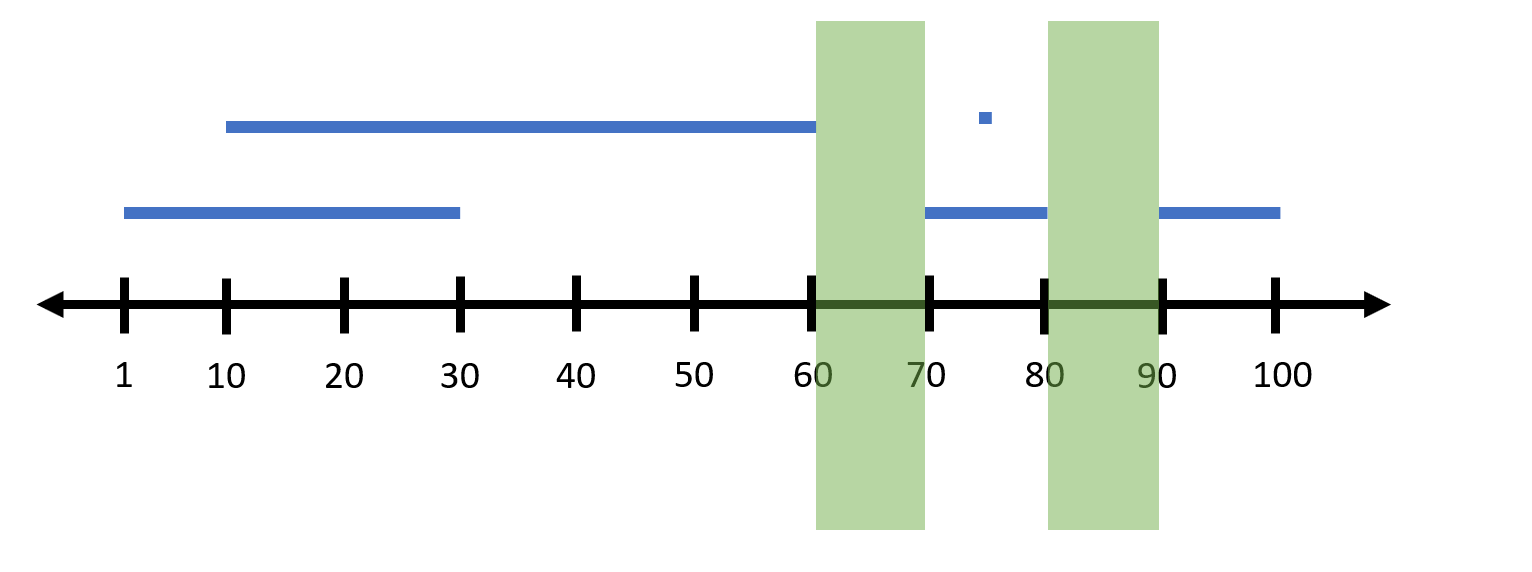
## ورودی نمونه ۲
```
1
1 100
```
## خروجی نمونه ۲
```
0
```
نیاز به حذف کردن هیچ بازهای نیست.
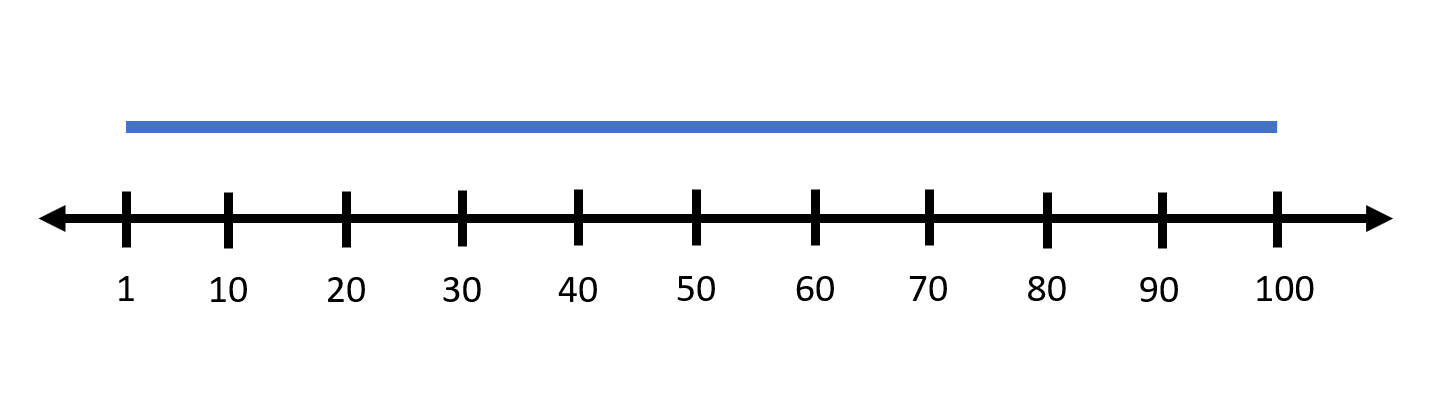
## ورودی نمونه ۳
```
1
2 99
```
## خروجی نمونه ۳
```
-1
```
بدون در نظر گرفتن بازههای مورد علاقه فقط بازه $[1, 2)$ و بازه $(99, 100]$ باقی میماند که نمی توان با تعداد متناهی بازه این دو بازه را پوشاند.
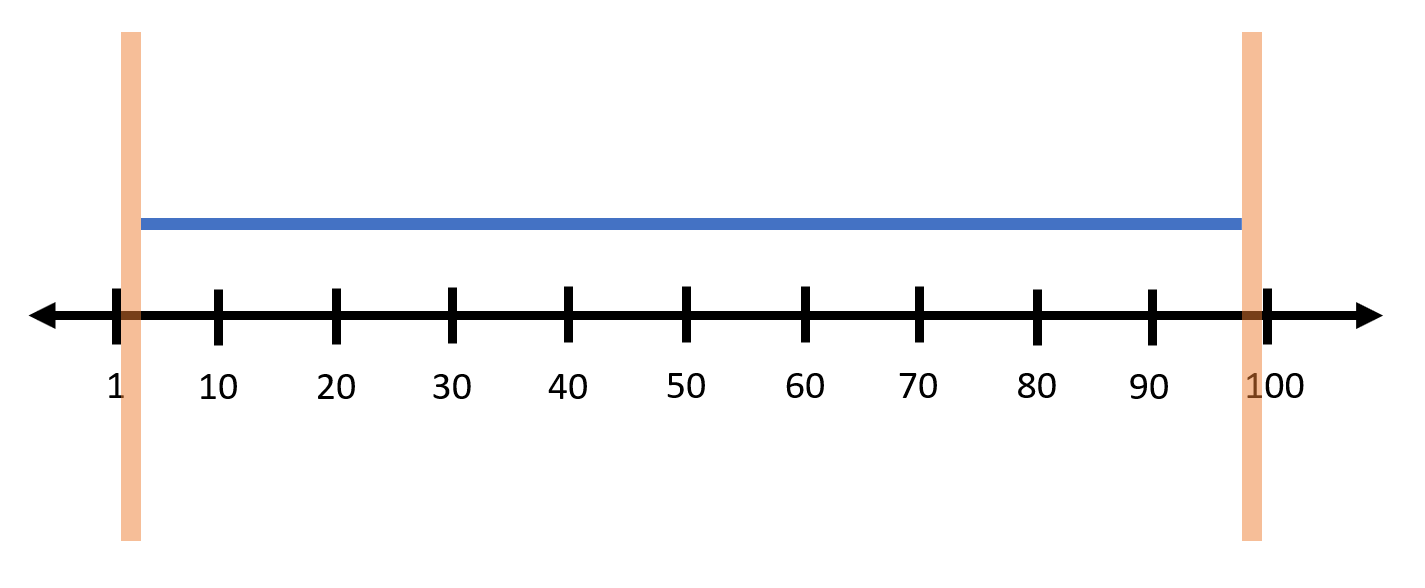
بازه حذف کردن
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
*امروز روز جهانیه ریاضیاته! و «نظریه گرافها» یکی از مدلهای باحال اونه...*

%align_center_start%
*دکتر مهدی بهزاد*
%align_end%
فرض کنید $G = (V, E)$ و $G' = (V', E')$ دو گراف ساده بدون جهت باشند. منظور $G \times G'$ یعنی گرافی که راسهای آن $V \times V'$ ([ضرب دکارتی](https://fa.wikipedia.org/wiki/%D8%B6%D8%B1%D8%A8_%D8%AF%DA%A9%D8%A7%D8%B1%D8%AA%DB%8C)) باشد و یک یال بین دو راس $(v, v')$ و $(u, u')$ وجود دارد اگر و تنها اگر $v = u$ و $v'u'$ یالی در $G'$ باشد یا $v' = u'$ و $vu$ یالی در $G$ باشد.
به همین ترتیب میتوان تعریف را تعمیم داد و $k$ گراف را در هم ضرب کرد!
حال فرض کنید گراف $G$ داده شده است و منظور از $G^k$ گرافی است که از $k$ بار ضرب شدن $G$ در خودش بدست میآید.
میدانیم راسهای $G^k$ دنبالههایی به طول $k$ از راسهای $G$ خواهند بود. دو راس $v_1, v_2, \dots, v_k$ و $u_1, u_2, \dots, u_k$ در این گراف را در نظر بگیرید. این دو راس به هم با یک یال متصل خواهند بود اگر و تنها اگر یک اندیس $i$ وجود داشته باشد که $v_i$ و $u_i$ در گراف $G$ با یک یال به هم متصل باشند و به ازای همهی اندیسهای $j$ که $i \neq j$ داشته باشیم $v_j = u_j$.
به شما دو راس از $G^k$ داده میشود و شما باید طول کوتاه ترین مسیر بین این دو راس را محاسبه کنید.
# ورودی
در سطر اول ورودی دو عدد صحیح و مثبت $n$ و $m$ داده میشود که به ترتیب نشاندهندهی تعداد راسها و یالهای $G$ است.
$$1 \leq n \leq 500$$
$$0 \leq m \leq \frac{n(n - 1)}{2}$$
در $m$ سطر بعدی در هر سطر دو عدد صحیح و مثبت $u$ و $v$ آمده که نشاندهندهی یال گراف $G$ است.
$$1 \leq u \neq v \leq n$$
تضمین میشود هیچ یالی دوبار ظاهر نشود یعنی $G$ گرافی ساده خواهد بود.
در سطر بعدی عدد صحیح و مثبت $k$ آمده است.
$$1 \leq k \leq 500 \ 000$$
در سطر بعدی $k$ عدد صحیح و مثبت $v_1, v_2, \dots, v_k$ با فاصله آمده است و در سطر بعدی $k$ عدد صحیح و مثبت $u_1, u_2, \dots, u_k$ آمده است و به ترتیب نشاندهنده دو راس در $G^k$ هستند.
$$ 1 \le u_i, v_i \le n $$
# خروجی
در تنها سطر خروجی پاسخ مسئله یعنی کوتاه ترین مسیر بین این دو راس را چاپ کنید. در صورتی که مسیری بین این دو راس وجود نداشته باشد عدد منفی یک را چاپ کنید.
# مثال
## ورودی نمونه ۱
```
3 2
1 2
2 3
3
1 2 3
1 3 1
```
## خروجی نمونه ۱
```
3
```
گراف داده شده به صورت زیر است:
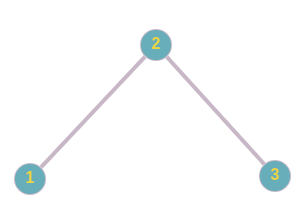
دنباله مسیر از $(1, 2, 3)$ به $(1, 3, 1)$ به صورت زیر خواهد بود.
$$(1, 2, 3) \to (1, 3, 3) \to (1, 3, 2) \to (1, 3, 1)$$
## ورودی نمونه ۲
```
4 2
1 2
3 4
2
1 4
2 2
```
## خروجی نمونه ۲
```
-1
```
گراف داده شده به صورت زیر است:
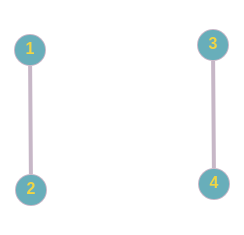
و هیچ مسیری از $(1, 4)$ به $(2, 2)$ وجود ندارد.
ضرب گرافها
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
*امروز روز جهانیه ریاضیاته! و «بهینهسازی» یکی از کاربردی ترین مباحث اونه...*

%align_center_start%
*دکتر غلامحسین مصاحب*
%align_end%
مجموعهای از فایلها داریم و قصد داریم آنها را فقط با استفاده از یک فلش، از کامپیوتر مبدا به کامپیوتر مقصد منتقل کنیم.
در هر انتقال زیرمجموعهای از این فایلها را انتخاب میکنیم و همه را روی فلش ریخته و در کامپیوتر مقصد خالی میکنیم، با رعایت این نکته که حجم این زیرمجموعه از فایلها نباید از ظرفیت فلش بیشتر شود.
ما بینهایت تنبل هستیم در نتیجه میخواهیم با **کمترین تعداد انتقال** این کار را انجام دهیم. از آنجایی که شما برنامهنویسی بلد هستید، با گرفتن تعداد و حجم فایلها به همراه ظرفیت فلش در ورودی، این کمترین تعداد بار را خروجی چاپ کنید.
# ورودی
در خط اول ورودی دو عدد طبیعی $n$ و $C$ با یک فاصله از هم آمدهاند که به ترتیب تعداد فایلها و ظرفیت فلش را مشخص میکنند.
$$
1 \le n \le 18
$$
$$
1 \le C \le 100
$$
در خط دوم $n$ عدد طبیعی با فاصله از هم آمدهاند. عدد $i$ام، $v_i$ است که حجم فایل $i$ام را مشخص میکند.
$$
1 \le v_i \le C
$$
# خروجی
در تنها خط خروجی کمترین تعداد انتقال این فایلها روی فلش را خروجی دهید.
## ورودی نمونه ۱
```
3 10
2 4 3
```
## خروجی نمونه ۱
```
1
```
مجموع حجم سه فایل میشود ۹ که از ظرفیت فلش(۱۰) کمتر است، پس تنها با یک بار انتقال میتوانیم به خواستهی مسئله برسیم.
## ورودی نمونه ۲
```
4 15
2 10 5 13
```
## خروجی نمونه ۲
```
2
```
در راه حل بهینه، ابتدا دو فایل با حجمهای ۲ و ۱۳ و در دور دوم فایلهای با حجم ۱۰ و ۵ را منتقل میکنیم.
انتقال با فلش
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۶۴ مگابایت
----------
*امروز روز جهانیه ریاضیاته! و «جبر مجرد» یکی از جامعترین و انتزاعیترین قسمتهای اونه...*

%align_center_start%
*دکتر پرویز شهریاری*
%align_end%
به یک دنباله از اعداد طبیعی مانند $d_1, d_2, \dots, d_k \,$
«$n$-آبِلی» گوییم. اگر سه شرط زیر برقرار باشد:
### شرط اول
همه اعداد دنباله بزرگتر از ۱ باشند. به عبارت دیگر:
$$1 < d_1, \quad 1 < d_2, \quad \dots \quad 1 < d_k$$
### شرط دوم
ضرب همه اعداد موجود در دنباله برابر $n$ باشد. به عبارت دیگر:
$$d_1 \times d_2 \times \dots \times d_k = n$$
### شرط سوم
در صورتی که طول دنباله بیشتر از ۱ باشد هر عدد در این دنباله به عدد بعدی بخشپذیر است. به عبارت دیگر:
$$d_1 | d_2, \quad d_2 | d_3 \quad \dots \quad d_{k - 1} | d_k$$
توجه کنید در دنبالههای به طول ۱ شرط سوم همواره برقرار است.
عدد طبیعی $n$ به شما داده میشود و از شما میخواهیم تعداد دنبالههای «$n$-آبلی» را محاسبه کنید.
# ورودی
در تنها سطر ورودی یک عدد صحیح و مثبت $n$ آمده است.
$$2 \leq n \leq 10^{18}$$
# خروجی
در تنها سطر خروجی یک عدد صحیح و مثبت که نشاندهندهی تعداد دنبالههای $n$-آبِلی است را چاپ کنید.
# مثال
## ورودی نمونه ۱
```
5
```
## خروجی نمونه ۱
```
1
```
تنها دنباله ۵-آبِلی دنباله «$5$» است.
## ورودی نمونه ۲
```
6
```
## خروجی نمونه ۲
```
1
```
تنها دنباله ۶-آبِلی دنباله «$6$» است.
## ورودی نمونه ۳
```
8
```
## خروجی نمونه ۳
```
3
```
سه دنباله ۸-آبِلی وجود دارد. دنباله «$8$» و «$2, 4$» و «$2, 2, 2$».
گروههای آبِلی
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
*امروز روز جهانیه ریاضیاته! و «ماتریسها و جبرخطی» یکی از کاملترین مدلهاست...*

%align_center_start%
*دکتر لطفی زاده*
%align_end%
منظور از یک ماتریس یک جدول است که سطرهای آن از بالا به پایین از $1$ تا $n$ شمارهگذاری شده است. ستونهای آن از چپ به راست از $1$ تا $m$ شماره گذاری شده است.
منظور از «درایه» $(x, y)$ یک ماتریس یعنی عدد نوشته شده در سطر $x$ام و ستون $y$ام.
منظور از «زیرماتریس» $(x_1, y_1)$ و $(x_2, y_2)$ که $x_1 \leq x_2$ و $y_1 \leq y_2$ است یعنی تمام درایههایی مثل $(x, y)$ که:
$$x_1 \leq x \leq x_2, \quad y_1 \leq y \leq y_2$$
یک ماتریس (همان جدول) $n \times m$ داریم که ابتدا همه درایههای آن **صفر** است.
ابتدا علی یک زیرماتریس از آن را انتخاب میکند و همه درایههای آن را یک واحد **افزایش** میدهد.
سپس امین یک زیرماتریس از آن را انتخاب میکند و همه درایههای آن را یک واحد **کاهش** میدهد.
پس درایههای ماتریس نهایی برابر $0$، $1$ یا $-1$ است. برای راحتتر نشان دادن این ماتریس، درایههای $0$ را با `.`، درایههای $1$ را با `+` و درایههای $-1$ را با `-` نشانمیدهیم.
اکنون فقط ماتریس نهایی را داریم و میخواهیم در صورتی که زیرماتریس انتخابی علی و امین **یکتا** پیدا میشود به ترتیب آنها را چاپ کنید یا بگوییم نمیتوان به صورت یکتا جواب را مشخص کرد.
تضمین میشود جدول داده شده واقعاً حاصل کار علی و امین بعد از این عملیات باشد. (یعنی حداقل یک جواب وجود دارد.)
# ورودی
در سطر اول ورودی عدد صحیح و مثبت $t$ آمده که تعداد تستکیسها را نشان میدهد.
$$1 \leq t \leq 1000\ 000$$
سپس برای هر تست ابتدا در یک سطر دو عدد صحیح $n$ و $m$ با فاصله از هم آمده است.
$$1 \le n, m \le 1000$$
در $n$ سطر بعدی در هر سطر $m$ عدد صحیح با فاصله میآید که این عدد نشان دهنده مقدار آرایه است.
تضمین میشود که مجموع $nm$ به ازای همه تستها از $1000 \ 000$ تجاوز نمیکند.
# خروجی
برای هر کدام از $t$ تست در صورتی که جواب مسئله یکتاست کلمه `unique` و در غیر اینصورت کلمه `not unique` را چاپ کنید.
در صورت یکتایی در دو سطر بعدی در هر سطر به ترتیب چهار عدد $x_1, y_1, x_2, y_2$ را چاپ کنید که به ترتیب زیرماتریسهای انتخابی امین و علی را نشان میدهد.
# مثال
## ورودی نمونه
```
3
5 5
+++..
+++..
+..--
.----
.....
3 6
+++++.
+....-
.-----
3 3
+..
+..
+..
```
## خروجی نمونه
```
unique
1 1 3 3
3 2 4 5
unique
1 1 2 5
2 2 3 6
not unique
```
تصویر مربوط به تست اول:
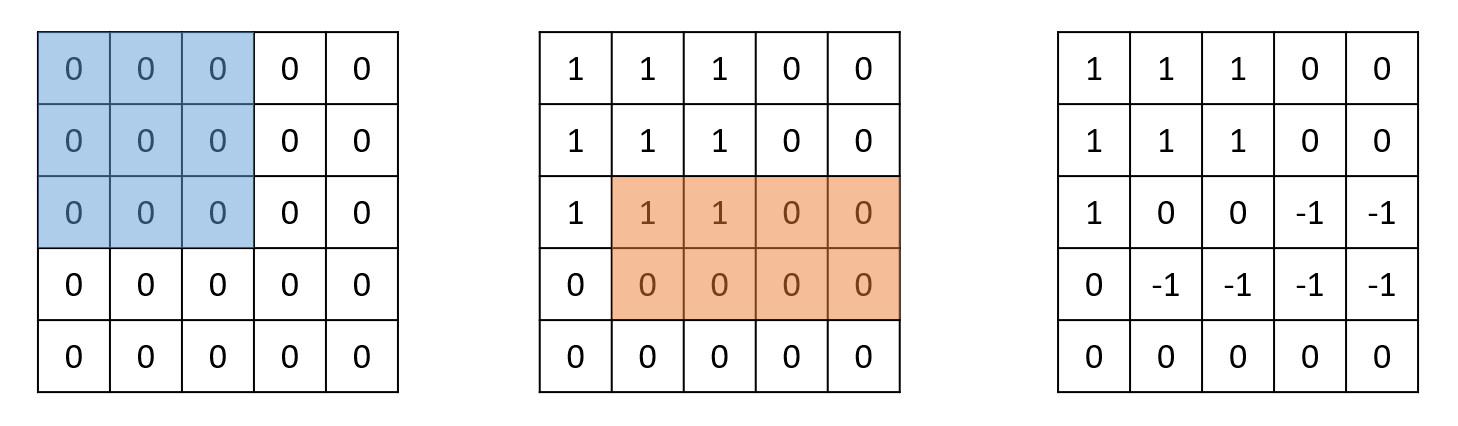
تصویر مربوط به تست دوم:
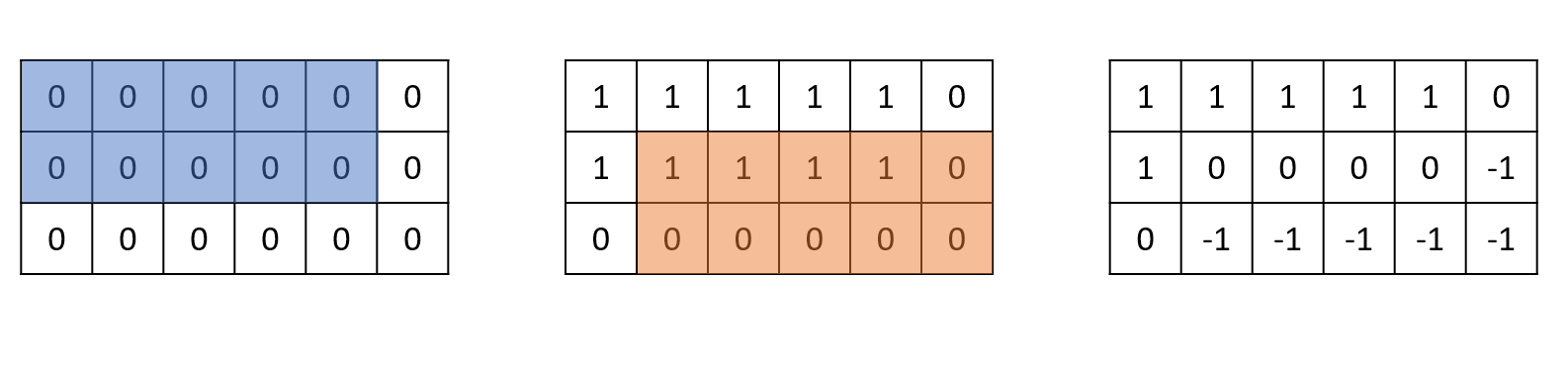
تصویر مربوط به تست سوم:
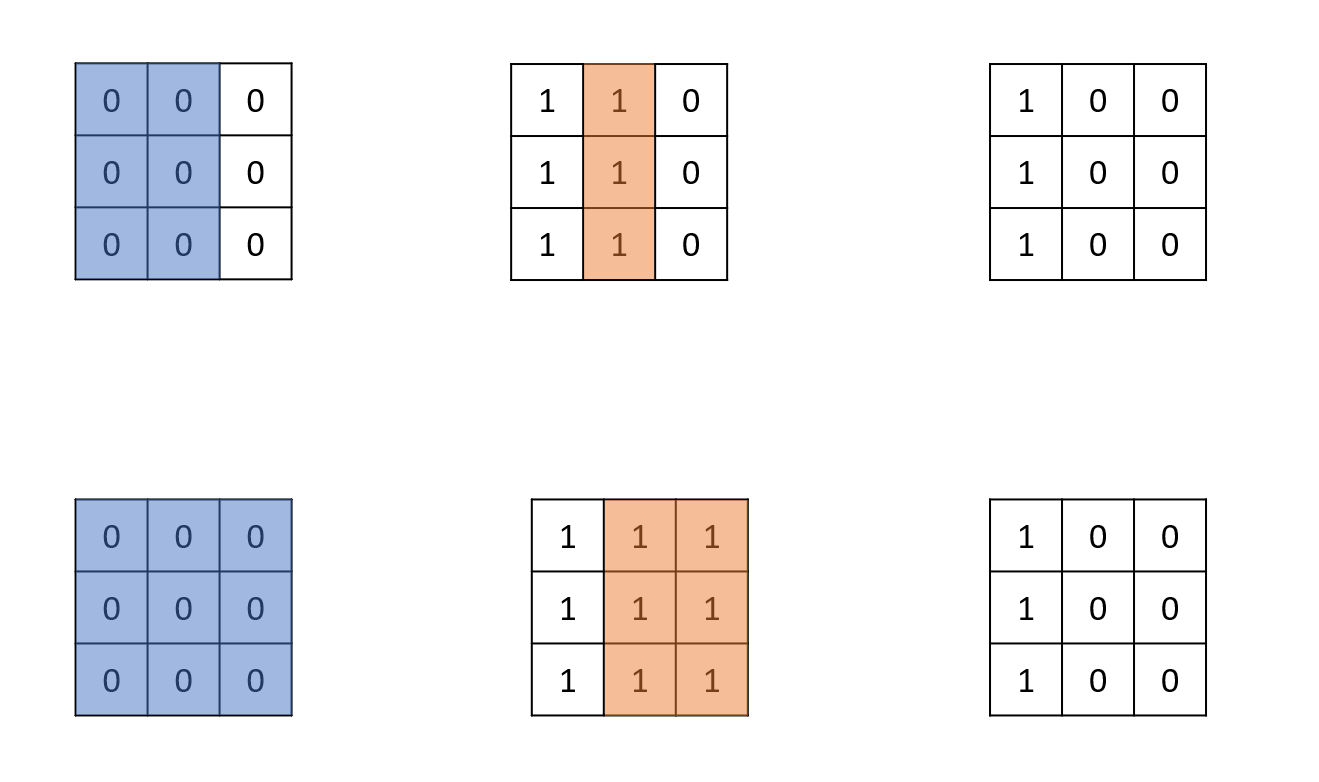
دو مستطیل
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
*امروز روز جهانیه ریاضیاته! و «ترکیبیات» یکی از پیچیدهترین مباحث اونه...*

%align_center_start%
*دکتر فریدون درخشانی*
%align_end%
در کوئرا $n$ نفر مشغول به کارند. این $n$ نفر را با اعداد $1, 2, 3, \dots ,n$ نشان میدهیم. سیستم کاری شرکت به صورت یک درخت ریشهدار است. یعنی هر کس به جز مدیرعامل (که با عدد $1$ نشان داده میشود.) یک مدیر دارد. مدیر کارمند با شماره $i$ را با $par_i$ نشان میدهیم. همواره $par_i < i$ است.
یک روز یک شعبده باز وارد کوئرا میشود و میخواهد اعضای شرکت را به چالش بکشد.
روند شعبده بازی به صورت زیر است:
شعبده باز میخواهد روی سر هر کدام از اعضای شرکت یک کلاه قرار دهد. هر کلاه میتواند به یکی از $c$ رنگ $1, 2, 3, \dots, c$ رنگآمیزی شده باشد. هیچ کس رنگ کلاه روی سرش را نمیبیند و فقط میتوند رنگ کلاه مدیر خود و اعضایی از شرکت را ببیند که مدیر مستقیم آنان است. (همه اعضای شرکت مقدار $c$ و ساختار درختی شرکت را میدانند.)
بعد از پایان کلاه گذاری هر کس یک حدس خصوصی درباره رنگ کلاه خودش میزند. (یعنی این حدس را بلند اعلام نمیکند و هیچ کس حدس هیچ کسی را نمیبیند.) توجه کنید بعد از شروع کلاه گذاری توسط شعبده باز هیچ ارتباطی بین اعضای شرکت مجاز نیست و فقط رنگ کلاه مدیر و زیردستان قابل روئیت است.
هدف اعضای شرکت کوئرا بیشینه کردن مجموع حدسهای درست است.
بعد از اینکه شعبده باز قاعده بازی را توضیح داد به اعضای شرکت اجازه داد که کمی باهم مشورت کنند و به یک استراتژی دست جمعی برسند. (توجه کنید خود شعبده باز هم در شرکت حضور دارد و استراتژی را میداند.)
بعد از پایان مشورت کلاه گذاری توسط شعبده باز آغاز میشود. اگر فرض کنیم که اعضای کوئرا بهترین استراتژی را برای بیشینه کردن حدسها انتخاب میکند و شعبده باز هم کلاه گذاری را انتخاب میکند که کمترین حدس درست را اعضای شرکت بزنند. تعداد حدسهای درست در نهایت بیابید.
توجه کنید استراتژی اعضای شرکت نمیتواند به شانس بستگی داشته باشد و کاملا به صورت تصمیم پذیر حدسها را مشخص میکند. (یعنی قبل از هر روش کلاه گذاری، شعبده باز میتواند همه حدسها را بفهمد چون استراتژی اعضای شرکت را میداند.)
# ورودی
در سطر اول ورودی دو عدد صحیح و مثبت $n$ و $c$ که با یک فاصله از هم جدا شدهاند آمده است و به ترتیب نشان دهندهی تعداد اعضای شرکت و تعداد رنگهای مختلف کلاهها است.
$$2 \leq n \leq 100 \, 000$$
$$1 \leq c \leq 10 $$
در سطر دوم ورودی $n - 1$ عدد صحیح و مثبت با فاصله از هم آمده است که عدد $i$ام شماره مدیر عضو $i + 1$ام یا همان $par_{i+1}$ را نشان میدهد.
$$par_{i +1} \leq i $$
# خروجی
در تنها سطر خروجی بیشینه حدس درست که اعضای کوئرا میتوانند تضمین کنند خواهند داشت را چاپ کنید.
# مثال
## ورودی نمونه ۱
```
2 3
1
```
## خروجی نمونه ۱
```
0
```
هر استراتژی که اعضای شرکت داشته باشند، شعبدهباز میتواند طوری کلاهها را روی سر اعضای شرکت بگذارد که هیچ کدام از اعضا نتوانند حدس درستی بزنند.
## ورودی نمونه ۲
```
2 2
1
```
## خروجی نمونه ۲
```
1
```
در این ساختار شرکت، ۱ رنگ کلاه ۲ و ۲ رنگ کلاه ۱ را میبیند. استراتژی اعضای شرکت به این صورت است که ۱ رنگ کلاه ۲ و ۲ رنگ مخالف کلاه ۱ را حدس میزند. بنابراین اگر رنگ کلاه این دو نفر یکسان باشد حدس ۱ و اگر رنگ کلاه این دو نفر متفاوت باشد حدس ۲ درست خواهد بود. پس این استراتژی همواره یک حدس درست به ازای هر روش کلاهگذاری ایجاد میکند. همچنین هیچ استراتژی وجود ندارد که بتوان با کمک آن ۲ حدس درست ایجاد کرد.
## ورودی نمونه ۳
```
5 1
1 2 2 4
```
## خروجی نمونه ۳
```
5
```
در این حالت هر کس میتواند رنگ کلاه خودش را به درستی حدس بزند.