+ محدودیت زمان سی پلاس پلاس: ۱ ثانیه
+ محدودیت زمان جاوا: ۲ ثانیه
+ محدودیت زمان پایتون: ۳ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
تعدادی تانک در یک صف قرار دارند و برای اینکه تانکی بتواند شلیک کند نباید تانک دیگری در جلوی آن باشد؛
برای حل این مشکل از آرایشهای جنگی استفاده میکنیم.
به عنوان فرمانده، تانکهای خود را طوری آرایش دهید که با کمترین جابهجایی در موقعیت مناسب قرار گیرند.
## آرایشها
1. **آرایش اول**: هر تانک با فاصله ۳ متر در سمت چپ تانک قبلی قرار میگیرد.
2. **آرایش دوم**: هر تانک با فاصله ۳ متر در سمت راست تانک قبلی قرار میگیرد.
## نکات
+ نمیتوانید موقعیت تانک اول را تغییر دهید و فقط با جابهجایی تانکهای دیگر باید به آرایش مورد نظر برسید.
+ اگر مجموع جابهجاییهای دو آرایش برابر شود، باید آرایش اول را به عنوان جواب انتخاب کنید.
# ورودی
در خط اول ورودی، $n$ میآید که بیانگر تعداد تانکهاست. سپس در خط بعد، مختصات $n$ تانک به ترتیب به صورت دنبالهای از $x_i$ها میآید.
$$ 5 \leq n \leq 10\ 000 $$
$$ -50\ 000 \leq x_i \leq 50\ 000 $$
# خروجی
در خروجی، مقدار جابهجایی هر تانک را به ترتیب در خطوط جداگانه چاپ کنید.
## ورودی نمونه ۱
```
6
3 -1 4 -1 6 2
```
## خروجی نمونه ۱
```
0
+1
-7
-5
-15
-14
```
<details>
<summary>توضیح نمونه ۱</summary>
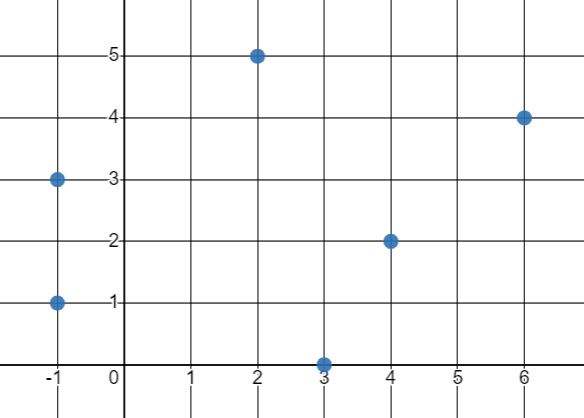
+ از آنجایی که موقعیت تانک اول باید ثابت باشه، همیشه مقدار جابهجایی آن ۰ است.
+ برای آنکه تانک دوم با فاصله ۳ متر در سمت چپ تانک اول قرار گیرد، باید ۱ متر به سمت راست جابهجا شود.
+ برای آنکه تانک سوم با فاصله ۳ متر در سمت چپ تانک دوم قرار گیرد، باید ۷ متر به سمت چپ جابهجا شود.
+ به همین صورت، تانکهای چهارم، پنجم و ششم باید به ترتیب ۵، ۱۵ و ۱۴ متر به سمت چپ جابهجا شوند.
مجموع این جابهجاییها ۴۲ متر است و به همین صورت مجموع جابهجاییهای آرایش دوم، برابر ۵۰ میشود؛ بنابراین آرایش اول را بهعنوان جواب انتخاب میکنیم.
</details>
## ورودی نمونه ۲
```
5
-8 -9 1 5 7
```
## خروجی نمونه ۲
```
0
+4
-3
-4
-3
```
<details>
<summary>توضیح نمونه ۲</summary>
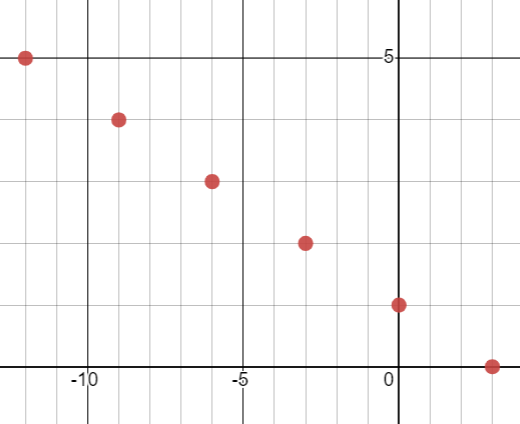
در صورتی که آرایش اول را انتخاب کنیم، باید تانکها را به ترتیب ۰، ۲-، ۱۵-، ۲۲- و ۲۷- متر جابهجا کنیم؛
اما اگر آرایش دوم را انتخاب کنیم، باید تانکها را به ترتیب ۰، ۴+، ۳-، ۴- و ۳- متر جابهجا کنیم؛
مجموع جابهجاییها در آرایش اول برابر با ۶۶ و در آرایش دوم برابر با ۱۴ میشود؛ بنابراین آرایش دوم را به عنوان جواب انتخاب میکنیم.
</details>
الگوریتمی - ژنرال
+ محدودیت زمان سی پلاس پلاس: ۱ ثانیه
+ محدودیت زمان جاوا: ۲ ثانیه
+ محدودیت زمان پایتون: ۱۰ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
تعدادی جنگنده در یک صف هستند و ارتفاع تمام آنها از زمین متمایز است. هر جنگنده تنها میتواند جنگندههای جلویی خود را هدف قرار دهد، با این شرط که ارتفاعشان از آن کمتر باشد.
تعداد جنگندههایی را که یک جنگنده میتواند مورد هدف قرار دهد، **عدد استراتژیک** مینامیم.
به عنوان مثال اگر جنگنده الف بتواند ۳ جنگنده را مورد هدف قرار دهد، میگوییم عدد استراتژیک جنگنده الف برابر با ۳ است.
مجموع اعداد استراتژیک تمام جنگندهها را بدست آورید.
# ورودی
در خط اول ورودی، $n$ میآید که بیانگر تعداد جنگندههاست. سپس در خط بعد، ارتفاع $n$ جنگنده به ترتیب به صورت دنبالهای از $h_i$ ها میآید.
$$ 1 \leq n \leq 100\ 000 $$
$$ 1 \leq h_i \leq 100\ 000 $$
# خروجی
در خروجی، مجموع اعداد استراتژیک تمام جنگندهها را چاپ کنید.
## ورودی نمونه ۱
```
5
5 4 3 7 6
```
## خروجی نمونه ۱
```
4
```
<details>
<summary>توضیح نمونه ۱</summary>
اولین جنگنده با ارتفاع ۵ از همه عقبتر است و امکان شلیک به جنگنده دوم و سوم را دارد. در نتیجه عدد استراتژیک آن ۲ است. جنگنده دوم میتواند جنگنده سوم را هدف قرار دهد و عدد استراتژیک آن ۱ است. جنگنده سوم امکان شلیک به جنگنده چهارم و پنجم را به دلیل ارتفاع کمتر ندارد و عدد استراتژیک آن ۰ است. به همین صورت عدد استراتژیک جنگنده چهارم، ۱ و جنگنده پنجم، ۰ است.
در نتیجه مجموع اعداد استراتژیک جنگندهها برابر ۴ خواهد بود.
</details>
## ورودی نمونه ۲
```
30
16 6 17 15 21 18 20 28 3 4 11 9 5 13 27 29 10 7 12 25 2 19 30 24 23 26 1 8 22 14
```
## خروجی نمونه ۲
```
202
```
الگوریتمی - نبرد هوایی
+ محدودیت زمان سی پلاس پلاس: ۲/۵ ثانیه
+ محدودیت زمان جاوا: ۳/۵ ثانیه
+ محدودیت زمان پایتون: ۵ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
در یک بازی مدیریت شهری، باید ۳ ساختمان را به شکلی مدیریت کنید که مصرف برق آنها به بهینهترین حالت ممکن برسد. برای فهمیدن این موضوع، داور بازی در هر مرحله $m$ کار انجام میدهد تا تعداد امتیازهای منفی را محاسبه کند. این کارها یکی از دو نوع زیر میباشند:
1. داور مصرف برق واحد $k$ام از ساختمان $a$ را به $x$ تغییر میدهد. به بیانی $a_k = x$.
2. داور با دادن مقدار $r$ به دنبال سه واحد $i$ و $j$ و $k$ از سه ساختمان $a$ و $b$ و $c$ میگردد که شرایط زیر را داشته باشند و به ازای هر بار یافتن این الگو یک امتیاز به بازیکن میدهد:
$$1≤i<j<k≤r$$
$$b_{a_i} = a_j = c_{a_k}$$
* **منظور از $a_i$ مصرف برق واحد $i$ام از ساختمان $a$ میباشد.**
# ورودی
در خط اول ورودی عدد $n$ به عنوان تعداد واحدهای سه ساختمان و $m$ به عنوان تعداد کارهایی که داور انجام میدهد داده میشوند.
$$ 1 \leq n \leq 200\ 000 $$
$$ 1 \leq m \leq 500\ 000 $$
در ادامه در سه خط سه دنباله به طول $n$ به ترتیب به عنوان مصرف برق واحدهای ساختمان $a$ و $b$ و $c$ داده میشود.
$$ 1 \leq a_i, b_i, c_i \leq n $$
در ادامه در $m$ خط کارهای داور میآیند که به قالب زیر هستند:
**CHANGE(k,x)** := عنصر $k$ام در دنبالۀ اول به $x$ تغییر میکند
**PRINT(r)** := کار نوع دوم است که در جوابش یک عدد (امتیازهایی که به بازیکن میدهد) باید بدهید
$$ 1 \leq k, x, r \leq n $$
# خروجی
به ازای هر پرسش نوع دوم، مقدار عددی خروجی را چاپ کنید.
## ورودی نمونه ۱
```
5 4
1 2 3 4 5
2 3 4 5 1
5 1 2 3 4
PRINT(5)
CHANGE(2,3)
PRINT(4)
PRINT(5)
```
## خروجی نمونه ۱
```
3
0
2
```
الگوریتمی - مدیریت شهری
+ محدودیت زمان جاوا: ۲ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
یک بازی تیراندازی اولشخص را تصور کنید؛ در این بازی انواع سلاح وجود دارد و هر سلاح نام، برد، قدرت و اندازۀ گلولۀ منحصربهفردی دارد. از طرفی گلولهها نیز اندازه و آسیب منحصربهفردی دارند که در ادامه آمده است.
## سلاحها
| نام | برد | قدرت | اندازۀ گلوله |
|:----------------:|:-------:|:------------:|:-------------:|
| Submachine Gun | 100 | 10 | 0.5 |
| Assault Rifle | 200 | 20 | 1 |
| Pistol | 80 | 8 | 0.5 |
| Shotgun | 50 | 40 | 4 |
| Sniper Rifle | 1000 | 30 | 3 |
## گلولهها
| نام | اندازه | آسیب |
|:---:|:------:|:--------:|
| A | 0.5 | 1 |
| B | 1 | 1.5 |
| C | 3 | 3 |
| D | 4 | 2 |
# پروژه اولیه
پروژه اولیه را از [این لینک](https://quera.org/contest/assignments/41562/download_problem_initial_project/139999) دانلود کنید.
<details class="blue">
<summary>ساختار فایلها</summary>
```
GunProblemExample.zip
├── Shooter.java
└── ShootingContract.java
```
</details>
# خواستههای مسئله
با توجه به انواع سلاحها و گلولهها یک کلاس ایجاد کنید که `Interface` زیر را پیادهسازی کند:
```java
public interface ShootingContract {
void setGunByName(String name) throws Exception;
void addBulletOfGivenSizeToGun(float size, int count) throws Exception;
float shootToTarget(int targetX, int targetY, int targetDistance, int aimX, int aimY) throws Exception;
}
```
در بالا، به ترتیب سه متد **انتخاب سلاح**، **اضافهکردن گلوله** و **شلیک به هدف** تعریف شدهاند که به توضیح آنها میپردازیم:
+ متد **انتخاب سلاح** با توجه به ورودی، یک سلاح را انتخاب میکند تا در ادامه از آن استفاده شود.
+ در صورتی که سلاحی با نام داده شده وجود نداشته باشد، باید یک `Exception` پرتاب شود.
+ این متد باید به حرف کوچک و بزرگ حساس باشد؛ به عنوان مثال سلاحی با نام `submachine gun` نداریم.
+ متد **انتخاب گلوله**، گلولههایی را با اندازه و تعداد دادهشده به سلاح اضافه میکند.
+ در صورتی که هر کدام از موارد زیر رخ دهد، باید یک `Exception` پرتاب شود:
+ سلاحی انتخاب نشده باشد.
+ گلوله با اسلحه همخوانی نداشته باشد.
+ تعداد منفی باشد.
+ گلولهای با اندازۀ دادهشده وجود نداشته باشد.
+ متد **شلیک به هدف**، پارامترهای مختصات هدف، فاصله تا آن و مختصات نقطهای که سلاح به آن اشاره میکند را از ورودی دریافت میکند و در خروجی، با استفاده از فرمولی که در ادامه میآید، میزان آسیبی که به هدف میرسد را برمیگرداند.
+ هدف، یک مربع به ضلع ۱۰ است.
+ مختصات گوشۀ پایین-چپ مربع در ورودی داده میشود.
+ برای محاسبۀ خروجی، به صورت زیر عمل میکنیم:
+ اگر مختصات نقطهای که سلاح به آن اشاره میکند خارج از ابعاد هدف باشد، عدد ۰ برگردانده شود.
+ اگر برد سلاح از فاصله کمتر باشد، عدد ۰ برگردانده شود.
+ در غیر این صورت، حاصلضرب قدرت اسلحه در آسیب گلوله برگردانده شود.
+ در صورتی که سلاحی انتخاب نشده باشد یا گلولهای نداشته باشد، باید یک `Exception` پرتاب شود.
# مثال
```java
public void caseA() {
ShootingContract implementation = new Shooter();
implementation.setGunByName("Submachine Gun");
implementation.addBulletOfGivenSizeToGun(0.5f, 5);
var damage = implementation.shootToTarget(0, 0, 20, 5, 5);
}
```
# نکات
- شما تنها مجاز به تغییر در فایل `Shooter.java` هستید. تغییرات در باقی فایلها نادیده گرفته میشود.
- توجه کنید که تمیزی کد مهم و در رتبهبندی نهایی تاثیرگذار است.
- برای ثبت پاسخ، پروژه را با ساختار زیر ارسال کنید.
```
[your-zip-file-name].zip
└── Shooter.java
```
پیادهسازی - تفنگبازی (جاوا)
+ محدودیت زمان پایتون: ۲ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
یک بازی تیراندازی اولشخص را تصور کنید؛ در این بازی انواع سلاح وجود دارد و هر سلاح نام، برد، قدرت و اندازۀ گلولۀ منحصربهفردی دارد. از طرفی گلولهها نیز اندازه و آسیب منحصربهفردی دارند که در ادامه آمده است.
## سلاحها
| نام | برد | قدرت | اندازۀ گلوله |
|:----------------:|:-------:|:------------:|:-------------:|
| Submachine Gun | 100 | 10 | 0.5 |
| Assault Rifle | 200 | 20 | 1 |
| Pistol | 80 | 8 | 0.5 |
| Shotgun | 50 | 40 | 4 |
| Sniper Rifle | 1000 | 30 | 3 |
## گلولهها
| نام | اندازه | آسیب |
|:---:|:------:|:--------:|
| A | 0.5 | 1 |
| B | 1 | 1.5 |
| C | 3 | 3 |
| D | 4 | 2 |
# پروژه اولیه
پروژه اولیه را از [این لینک](https://quera.org/contest/assignments/41562/download_problem_initial_project/143421) دانلود کنید.
<details class="blue">
<summary>ساختار فایلها</summary>
```
GunProblemSample.zip
├── Shooter.py
└── ShootingContract.py
```
</details>
# خواستههای مسئله
با توجه به انواع سلاحها و گلولهها کلاس زیر را پیادهسازی کند:
```python
class Shooter:
def set_gun_by_name(self, name: str) -> None:
pass
def add_bullet_of_given_size_to_gun(self, size: float, count: int) -> None:
pass
def shoot_to_target(self, target_x: int, target_y: int, target_distance: int, aim_x: int, aim_y: int) -> float:
pass
```
در بالا، به ترتیب سه متد **انتخاب سلاح**، **اضافهکردن گلوله** و **شلیک به هدف** تعریف شدهاند که به توضیح آنها میپردازیم:
+ متد **انتخاب سلاح** با توجه به ورودی، یک سلاح را انتخاب میکند تا در ادامه از آن استفاده شود.
+ در صورتی که سلاحی با نام داده شده وجود نداشته باشد، باید یک `Exception` پرتاب شود.
+ این متد باید به حرف کوچک و بزرگ حساس باشد؛ به عنوان مثال سلاحی با نام `submachine gun` نداریم.
+ متد **انتخاب گلوله**، گلولههایی را با اندازه و تعداد دادهشده به سلاح اضافه میکند.
+ در صورتی که هر کدام از موارد زیر رخ دهد، باید یک `Exception` پرتاب شود:
+ سلاحی انتخاب نشده باشد.
+ گلوله با اسلحه همخوانی نداشته باشد.
+ تعداد منفی باشد.
+ گلولهای با اندازۀ دادهشده وجود نداشته باشد.
+ متد **شلیک به هدف**، پارامترهای مختصات هدف، فاصله تا آن و مختصات نقطهای که سلاح به آن اشاره میکند را از ورودی دریافت میکند و در خروجی، با استفاده از فرمولی که در ادامه میآید، میزان آسیبی که به هدف میرسد را برمیگرداند.
+ هدف، یک مربع به ضلع ۱۰ است.
+ مختصات گوشۀ پایین-چپ مربع در ورودی داده میشود.
+ برای محاسبۀ خروجی، به صورت زیر عمل میکنیم:
+ اگر برد سلاح از فاصله کمتر باشد، عدد ۰ برگردانده شود.
+ در غیر این صورت، حاصلضرب قدرت اسلحه در آسیب گلوله برگردانده شود.
+ در صورتی که سلاحی انتخاب نشده باشد یا گلولهای نداشته باشد، باید یک `Exception` پرتاب شود.
# مثال
```python
shooter = Shooter()
shooter.set_gun_by_name('Submachine Gun')
shooter.add_bullet_of_given_size_to_gun(0.5, 1)
result = shooter.shoot_to_target(1, 1, 20, 5, 4)
# result should be 10
```
# نکات
- شما تنها مجاز به تغییر در فایل `Shooter.py` هستید. تغییرات در باقی فایلها نادیده گرفته میشود.
- توجه کنید که تمیزی کد مهم و در رتبهبندی نهایی تاثیرگذار است.
- برای ثبت پاسخ، پروژه را با ساختار زیر ارسال کنید.
```
[your-zip-file-name].zip
└── Shooter.py
```
پیادهسازی - تفنگبازی (پایتون)
+ محدودیت زمان جاوا: ۲ ثانیه
+ محدودیت زمان پایتون: ۳ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
میخواهیم یک بازی کیکپزی بسازیم که در آن یک کیک ساده با اندازۀ مشخص به بازیکن داده میشود و او باید با انجام دستورالعمل برنامهریزی شده، کیک نهایی را تحویل دهد.
# دستورات
### پختن کیک با اندازۀ دادهشده
```
BAKE height width
```
کیک اولیه را که مستطیلی با ارتفاع `height` و طول `width` از $o$هاست، با توجه به دستورالعمل میپزد و آن را چاپ میکند.
$$ 1 \leq height < 100 $$
$$ 1 \leq width < 100 $$
<details>
<summary>مثال</summary>
با اجرای دستور زیر:
```
BAKE 3 5
```
کیک اولیه، به این شکل خواهد شد:
```
ooooo
ooooo
ooooo
```
</details>
----
## فرمانهای افزودن عملیات به دستورالعمل
در ابتدای برنامه دستورالعمل خالی است. در نتیجه با اجرای فرمان پختن کیک، همان کیک اولیه خروجی داده میشود. با اجرای فرمانهای زیر میتوانیم به دستورالعمل، عملیات اضافه کنیم. حال اگر فرمان پخت کیک صادر شد، عملیاتهای افزوده شده به ترتیب روی کیک اولیه اجرا میشوند.
### ۱. افزودن خامه
```
ADD OPERATION => ADD CREAM
```
به بالا و طرفین آخرین طبقه کیک خامه (`C`) اضافه و عبارت `Done` را در خروجی چاپ میکند.
<details>
<summary>مثال</summary>
اگر کیک به این شکل باشد:
```
ooo
ooo
```
پس از انجام عملیات، به این شکل خواهد شد:
```
CCCCC
CoooC
CoooC
```
</details>
### ۲. افزودن طعم
```
ADD OPERATION => ADD flavor TO where
```
قسمتهایِ موردِ نظرِ آخرینِ طبقۀ کیک را به طعم مشخصشده آغشته و عبارت `Done` را در خروجی چاپ میکند.
`flavor` میتواند شکلات (`K`)، توت فرنگی (`S`) یا موز (`B`) باشد.
`where` میتواند بالا (`TOP`) یا طرفین (`SIDES`) باشد.
<details>
<summary>مثال</summary>
اگر کیک به این شکل باشد:
```
oooo
oooo
oooo
```
با اجرای دستور زیر:
```
ADD S TO TOP
```
به این شکل خواهد شد:
```
SSSS
oooo
oooo
```
</details>
### ۳. افزودن طبقه
```
ADD OPERATION => ADD LAYER
```
یک طبقه را با ابعاد کیک اولیه، بر روی کیک فعلی قرار میدهد و عبارت `Done` را در خروجی چاپ میکند.
<details>
<summary>مثال</summary>
اگر کیک اولیه ارتفاع ۲ و طول ۴ داشته و کیک فعلی به شکل زیر باشد:
```
CCCCCC
CBBBBC
CooooC
```
به این شکل خواهد شد:
```
oooo
oooo
CCCCCC
CBBBBC
CooooC
```
</details>
----
### پایان برنامه
```
END
```
با اجرای این دستور، برنامه پایان مییابد.
## نکات
+ در نظر داشته باشید که دستورها همواره روی آخرین طبقه کیک اعمال میشوند. برای مثال اگر بخواهیم یک لایه خامه اضافه کنیم، تنها روی آخرین طبقه آن را انجام میدهیم.
+ کیک همواره متقارن است. بنابراین امکان یکسان نبودن طول طبقهها را در نظر داشته باشید و فضای خالی را با space پر کنید. همچنین این امکان وجود دارد که طبقات بالایی طول بیشتری داشته باشند.
<details>
<summary>مثال</summary>
اگر کیک اولیه ارتفاع ۲ و طول ۳ داشته و کیک فعلی به شکل زیر باشد:
```
KKK
ooo
```
با اجرای ادامه دستوالعمل به شکل زیر ممکن است بشود:
```
CCCCC
CoooC
CoooC
KKK
ooo
```
</details>
# ورودی
در هر خط ورودی، یکی از دستوراتی که در بالا توضیح داده شد، میآید. برنامه با دستور `END` خاتمه مییابد.
# خروجی
با توجه به توضیحات بالا، به ازای هر دستور، خروجی مورد نظر را چاپ کنید.
## ورودی نمونه ۱
```
BAKE 1 1
ADD OPERATION => ADD CREAM
BAKE 2 3
ADD OPERATION => ADD K TO SIDES
BAKE 2 3
ADD OPERATION => ADD LAYER
BAKE 1 3
ADD OPERATION => ADD S TO SIDES
BAKE 1 3
ADD OPERATION => ADD B TO TOP
BAKE 1 3
END
```
## خروجی نمونه ۱
```
o
Done
CCCCC
CoooC
CoooC
Done
KCCCK
KoooK
KoooK
Done
ooo
KCCCK
KoooK
Done
SoS
KCCCK
KoooK
Done
BBB
KCCCK
KoooK
```