+ محدودیت زمان: ۰.۵ ثانیه
+ محدودیت حافظه: ۶۴ مگابایت
----------
یک تیر به سمت «سیبل تیراندازی» زیر پرتاب شده و امتیاز $p$ را دریافت کرده است.
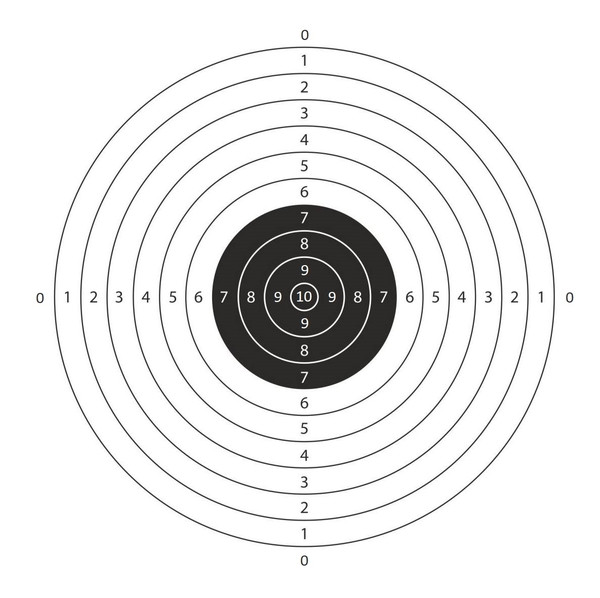
قوانین امتیازدهی به این صورت است که اگر تیر خارج از همه دایرهها باشد امتیاز ۰ را دریافت میکند و اگر تیر به هر کدام از نواحی شمارهگذاری شده برخورد کند، امتیاز آن ناحیه را دریافت میکند. (برای فهمیدن بهتر سوال به مثالها توجه کنید.)
از شما میخواهیم برنامهای بنویسید که با دریافت امتیاز کسبشده، تشخیص دهد که آیا تیر به «سیبل تیراندازی» برخورد کرده یا نه؛ اگر تیر به «سیبل تیراندازی» برخورد کرده، رنگ ناحیه برخورد را باتوجه به شکل بالا چاپ کنید.
# ورودی
در تنها سطر ورودی عدد صحیح $p$ آمده که نشاندهنده امتیاز دریافت شده است.
$$0 \leq p \leq 10$$
# خروجی
در تنها سطر خروجی، در صورتی که
+ تیر **خارج** از «سیبل تیراندازی» باشد عبارت `out`
+ تیر داخل «سیبل تیراندازی» باشد و ناحیه برخورد، **سفید** رنگ باشد عبارت `white`
+ تیر داخل «سیبل تیراندازی» باشد و ناحیه برخورد، **سیاه** رنگ باشد عبارت `black`
را چاپ کنید.
**توجه کنید سیستم داوری به بزرگی و کوچکی حروف حساس است.**
# مثال
## ورودی نمونه ۱
```
10
```
## خروجی نمونه ۱
```
black
```
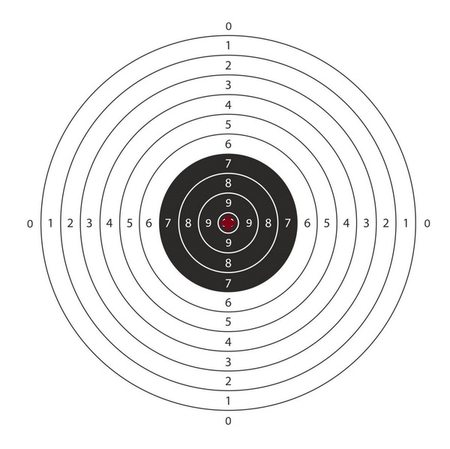
## ورودی نمونه ۲
```
3
```
## خروجی نمونه ۲
```
white
```
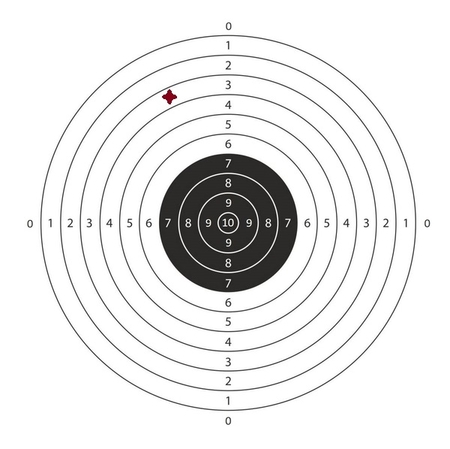
## ورودی نمونه ۳
```
7
```
## خروجی نمونه ۳
```
black
```
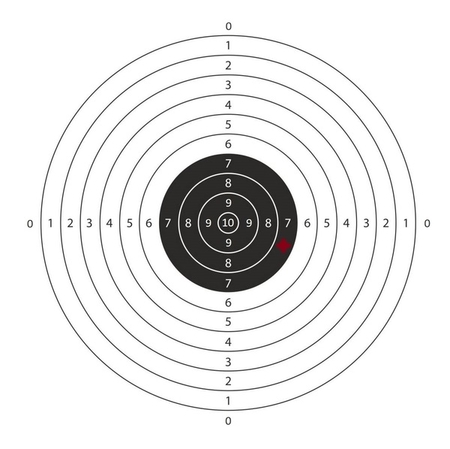
## ورودی نمونه ۴
```
0
```
## خروجی نمونه ۴
```
out
```
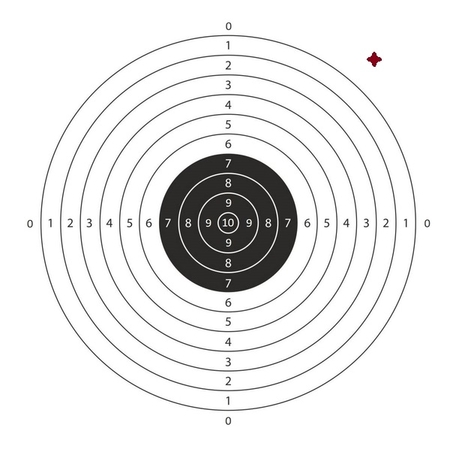
سیبل تیراندازی
+ محدودیت زمان: ۰.۵ ثانیه
+ محدودیت حافظه: ۶۴ مگابایت
----------
سعید $n$ ماه است که در کوئرا کار میکند. حقوق او در ماه $i$ام ($1 \leq i \leq n$) برابر $s_i$ بوده است. او یک شرایط سخت برای ادامه همکاری خود با کوئرا دارد و میخواهد **از این به بعد، حقوق هر ماه او برابر مجموع حقوق ماههای قبلی** باشد.
به عبارت دیگر:
+ حقوق ماه $n + 1$ام یا همان $s_{n+1}$ برابر $s_1 + s_2 + \dots + s_n \,$
+ حقوق ماه $n + 2$ام یا همان $s_{n+2}$ برابر $s_1 + s_2 + \dots + s_{n+1} \,$
+ حقوق ماه $n + 3$ام یا همان $s_{n+3}$ برابر $s_1 + s_2 + \dots + s_{n+2} \,$
+ و...
حال از شما $q$ سوال میپرسیم. در سوال $j$ام از شما میخواهیم میزان حقوق دریافتی این شخص در ماه $k_j$ام (یا همان $s_{k_j}$) را محاسبه کنید.
چون ممکن است این عدد خیلی بزرگ باشد، باقیمانده این عدد را بر $10^9+7$ محاسبه کنید.
# ورودی
در سطر اول ورودی به ترتیب دو عدد صحیح و مثبت $n$ و $q$ آمده است که به ترتیب نشاندهندهی تعداد ماههایی است که سعید تا کنون حقوق گرفته و تعداد سوالاتی که پرسیده خواهد شد.
$$1 \leq n, q \leq 100$$
در سطر دوم ورودی $n$ عدد صحیح و مثبت $s_1, s_2, \dots, s_n$ آمده است که حقوقهای دریافتی سعید در این $n$ ماه را نشان میدهد.
$$1 \leq a_i \leq 100$$
در $q$ سطر بعدی در هر سطر یک عدد صحیح و مثبت $k_j$ آمده است که یعنی حقوق دریافتی این شخص در ماه $k_j$ام را به پیمانه $10^9 + 7$ محاسبه کنید.
$$n + 1 \leq k_j \leq 1000 \ 000 \ 000$$
# خروجی
خروجی شامل $q$ سطر است که در سطر $j$ام آن، پاسخ سوال $j$ام، یعنی باقیمانده میزان حقوق دریافتی سعید در ماه $k_j$ بر $10^9+7$ را چاپ کنید.
# مثال
## ورودی نمونه ۱
```
3 2
1 2 3
4
5
```
## خروجی نمونه ۱
```
6
12
```
حقوق ماه ۴ام او ۶ و حقوق ماه ۵ام برابر ۱۲ است.
## ورودی نمونه ۲
```
5 1
1 1 1 1 1
1401
```
## خروجی نمونه ۲
```
349521860
```
توجه کنید پاسخ اصلی مسئله یک عدد بسیار بزرگ است، اما در این سوال کافی است باقیمانده این عدد را بر $10^9+7$ محاسبه کنید.
حقوق سعید
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
یک آرایه به طول $n$ از اعداد صحیح مثل $a_1, \dots, a_n$ داریم.
برای مثال این آرایه به طول ۳ و به شکل $[7, 5, 5]$ باشد.
در هر عملیات میتوانیم دو عدد صحیح و مثبت مثل $i$ و $j$ که $1 \leq i, j \leq n$ باشد را انتخاب کنیم و مقدار $a_i$ را به $a_j$ تبدیل کنیم. به عبارت دیگر میتوانیم دستور $a_i = a_j$ را اجرا کنیم.
برای مثال در آرایه بالا میتوانیم مقدار $i$ را برابر ۱ و $j$ را برابر ۳ انتخاب کنیم و عملیات گفته شده یعنی مقدار $a_1$ را حذف و مقدار $a_3$ را بهجای آن بنویسیم. یعنی آرایه اولیه به $[7, 5, 7]$ تبدیل میشود.
میتوانیم عملیات گفته شده را به تعداد دلخواه و بدون محدودیت روی آرایه $a$ انجام دهیم. هدف این است که این آرایه را به آرایه $b$ تبدیل کنیم.
بررسی کنید آیا رسیدن از آرایه $a$ به آرایه $b$ با انجام دادن تعداد دلخواهی از عملیات بالا شدنی است یا خیر.
# ورودی
در سطر اول ورودی عدد صحیح و مثبت $t$ آمده که تعداد تستهایی که در یک ورودی آمده را نشان میدهد.
$$1 \leq t \leq 100 \ 000$$
در سطر اول هر تست، عدد صحیح و مثبت $n$ آمده که طول دو آرایه $a$ و $b$ را نشان میدهد.
$$1 \leq n \leq 100 \ 000$$
در سطر دوم هر تست، $n$ عدد صحیح و مثبت $a_1, a_2, \dots, a_n$ که با یک فاصله از هم جدا شدهاند، آمده است.
در سطر سوم هر تست، $n$ عدد صحیح و مثبت $b_1, b_2, \dots, b_n$ که با یک فاصله از هم جدا شدهاند، آمده است.
$$1 \leq a_i, b_i \leq 10^9$$
**تضمین میشود مجموع $n$ها به ازای همه $t$ در یک ورودی، از ۱۰۰،۰۰۰ بیشتر نمیشود.**
# خروجی
به ازای هر تست در صورتی که میتوان از آرایه $a$ به آرایه $b$ با عملیات تعریف شده رسید `YES` و در غیر اینصورت `NO` را در یک سطر جداگانه چاپ کنید.
**توجه کنید سیستم داوری به کوچک و بزرگ بودن حروف حساس است.**
# مثال
## ورودی نمونه ۱
```
3
3
7 5 5
7 5 7
4
1 2 3 4
1 1 1 3
1
9
11
```
## خروجی نمونه ۱
```
YES
YES
NO
```
#### تست اول
همانطور که در صورت سوال گفته شد، آرایه $a$، با انجام دادن یک عملیات قابل تبدیل به آرایه $b$ است.
#### تست دوم
برای تبدیل آرایه $a$ به $b$ میتوانیم عملیاتها را به ترتیب و به صورت زیر انجام دهیم.
عملیات اول. مقدار $i$ برابر ۲ و مقدار $j$ برابر ۱ باشد. با قرار دادن $a_1$ به جای $a_2$ آرایه به صورت زیر خواهد شد.
$$[1, 1, 3, 4]$$
عملیات دوم. مقدار $i$ برابر ۴ و مقدار $j$ برابر ۳ باشد. با قرار دادن $a_3$ به جای $a_4$ آرایه به صورت زیر خواهد شد.
$$[1, 1, 3, 3]$$
عملیات سوم. مقدار $i$ برابر ۳ و مقدار $j$ برابر ۱ باشد. با قرار دادن $a_1$ به جای $a_3$ آرایه به صورت زیر خواهد شد.
$$[1, 1, 1, 3]$$
پس با این آرایه از عملیات رسیدن به وضعیت آرایه $b$ شدنی است.
#### تست سوم
انجام دادن عملیات، هیچ تغییری در آرایه $a$ ایجاد نمیکند، بنابراین رسیدن به آرایه $b$ شدنی نیست.
انتساب آرایه
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
یک گراف ساده و **همبند** $n$ راسی و $m$ یالی داریم. میخواهیم روی هر راس این گراف یک عدد از مجموعه
$\{ 1, 2, 3, \dots, k\}$
بنویسیم.
اگر عدد نوشته شده روی راس $v$ را با $a_v$ و طول کوتاه ترین مسیر بین دو راس $u$ و $v$ را با $dist(u, v)$ نشان دهیم.
میخواهیم این عدد گذاری به گونهای انجام شود که برای هر دو راس از این گراف مثل $u$ و $v$ داشته باشیم.
$$dist(u, v) = |a_u - a_v|$$
از شما میخواهیم تعداد روشهای انجام این کار را مشخص کنید. از آنجایی که پاسخ مسئله میتواند خیلی بزرگ باشد باقیمانده پاسخ مسئله را بر $10^9 + 7$ را چاپ کنید.
# ورودی
خط اول ورودی به ترتیب سه عدد $n$ و $m$ و $k$ با فاصله از هم آمدهاند.
$$1 \le n \le 100\ 000$$
$$n - 1 \leq m \leq min(\frac{n(n - 1)}{2},100 \, 000)$$
$$1 \le k \le 10^9$$
در $m$ خط بعدی و در هر خط دو عدد $v$ و $u$ با فاصله از هم آمدهاند که نشاندهندهی یالی بین دو رأس $v$ و $u$ هستند.
$$1 \le v, u \le n$$
**تضمین میشود گراف ورودی، گرافی ساده و همبند است.**
# خروجی
# مثال
## ورودی نمونه ۱
```
2 1 3
1 2
```
## خروجی نمونه ۱
```
4
```
اگر عدد نوشته شده روی راس شماره $v$ را با $c(v)$ نشان دهیم؛ ۴ روش زیر برای این عدد گذاری وجود دارد.
+ $c(1) = 1, c(2) = 2$
+ $c(1) = 2, c(2) = 1$
+ $c(1) = 3, c(2) = 2$
+ $c(1) = 2, c(2) = 3$
## ورودی نمونه ۲
```
3 3 2
1 2
2 3
3 1
```
## خروجی نمونه ۲
```
0
```
در گراف بالا هیچ عدد گذاری قابل قبولی وجود ندارد، چون به ازای هر عددگذاری حداقل دو راس مجاور وجود دارد که عدد نوشته شده روی آنها یکسان خواهند داشت و این با خواسته سوال تناقض دارد.
عددگذاری گراف
+ محدودیت زمان: ۲ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
عدد صحیح و مثبت $n$ به شما داده میشود.
از شما میخواهیم یک دنباله از اعداد صحیح مثبت، مثل $a_1, a_2, \dots, a_{2n} \,$ چاپ کنید که هر همه شرایط زیر را داشته باشد.
+ هر دو عدد متوالی در این دنباله مثل $a_i$ و $a_{i+1}$ نباید نسبت به هم اول باشند. (یعنی باید عامل مشترک بزرگتر از ۱ داشته باشند.)
+ همه اعداد $2$ تا $n$ در این دنباله آمده باشد.
+ همه اعداد این دنباله باید متمایز باشد.
در این سوال جواب مسئله لزوما یکتا نیست و شما هر دنبالهای که دلتان میخواهد (که شرایط فوق را دارد) میتوانید چاپ کنید.
درصورتی که دنباله شما شرایط فوق را داشته باشد نمره کامل را دریافت خواهید کرد.
# ورودی
هر ورودی شامل $t$ تست است؛ در هر کدام از $t$ سطر بعدی، در سطر $i$ام یک عدد صحیح و مثبت $n$ آمده که شما باید پاسخ مسئله را به ازای این تست چاپ کنید.
$$1 \leq t \leq 100$$
$$ 2 \leq n \leq 10000$$
**تضمین میشود مجموع $n$ها در همهی $t$ تست از ۱۰۰،۰۰۰ بیشتر نشود.**
# خروجی
خروجی شامل $t$ سطر است و در سطر $i$ام آن دنباله مورد نظر تست $i$ام را باید چاپ کنید که شامل $2n$ عدد صحیح و مثبت $a_1, a_2, \dots, a_{2n}$ که با یک فاصله از هم جدا شدهاند را چاپ کنید.
**در دنبالهای که چاپ میکنید نباید اعداد از یک میلیارد بیشتر یا مساوی شوند.**
$$1 \leq a_i < 10^9$$
# مثال
## ورودی نمونه ۱
```
3
4
2
3
```
## خروجی نمونه ۱
```
2 4 8 16 32 64 12 3
24 2 4 6
3 6 2 1402 2022 702
```
توجه کنید ممکن است خروجی برنامه شما برای این نمونه متفاوت باشد اما بازهم پاسخ درستی به مسئله داده باشید.
دنباله دلخواه
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
دنباله $\{f_n\}$ به این صورت ساخته میشود:
اگر $n = 1$ باشد:
$$f_{n} = 1$$
اگر $n > 1$ باشد:
$$f_{n} = gcd(f_{n - 1}, n) + n^2$$
منظور از $gcd(a, b)$ یعنی بزرگترین مقسومعلیه مشترک $a$ و $b$ است.
از شما میخواهیم به ازای $t$ مقدار مختلف برای $n$ مقدار $f_{n}$ را پیدا کنید.
# ورودی
در سطر اول ورودی عدد صحیح و مثبت $t$ آمده است.
$$1 \le t \le 1\,000\,000$$
در $t$ سطر بعدی، در هر سطر یک عدد صحیح و مثبت $n$ داده میشود.
$$1 \le n \le 1000 \ 000 \ 000$$
# خروجی
خروجی شامل $t$ سطر است که در سطر $n$ام آن مقدار $f$ به ازای عدد $i$ام داده شده در ورودی را چاپ کنید.
# مثال
## ورودی نمونه ۱
```
5
1
2
3
4
5
```
## خروجی نمونه ۱
```
1
5
10
18
26
```
+ $f(1) = 1$
+ $f(2) = gcd(f(1), 2) + 2^2 = gcd(1, 2) + 4 = 1 + 4 = 5$
+ $f(3) = gcd(f(2), 3) + 3^2 = gcd(5, 3) + 9 = 1 + 9 = 10$
+ $f(4) = gcd(f(3), 4) + 4^2 = gcd(10, 4) + 16 = 2 + 16 = 18$
+ $f(5) = gcd(f(4), 5) + 5^2 = gcd(18, 5) + 25 = 1 + 25 = 26$
دنباله غریب
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
یک جدول $n \times m$ داریم. این جدول شامل $n$ سطر و $m$ ستون است که به ترتیب از بالا به پایین از ۱ تا $n$ و از چپ به راست از ۱ تا $m$ شماره گذاری شده است. در هر خانه از این جدول یک لامپ خاموش قرار دارد.
در هر مرحله میتوانیم یک خانه از این جدول را انتخاب کنیم و آن لامپ و همه لامپهای مجاور ضلعی آن را تغییر وضعیت بدهیم. دو خانه مجاورند اگر در یک ضلع مشترک باشند
از شما میخواهیم با انجام دادن حداکثر $n \times m$ عملیات وضعیت همه لامپها را به روشن تبدیل کنید.
# ورودی
در تنها سطر ورودی دو عدد صحیح و مثبت $n$ و $m$ که با فاصله از هم جدا شدهاند آمده است.
$$1 \leq n, m \leq 1000$$
**تضمین میشود همواره راهی برای رسیدن به این هدف وجود دارد.**
# خروجی
در سطر اول خروجی عدد صحیح $k$ را چاپ کنید که تعداد عملیاتهای مورد نیاز شما را نشان میدهد.
$$0 \leq k \leq n \times m$$
در $k$ سطر بعدی، در سطر $i$ام، دو عدد صحیح و مثبت $r_i$ و $c_i$ را که با یک فاصله از هم جدا شدهاند چاپ کنید که به ترتیب نشاندهندهی سطر و ستون لامپی است که روی آن عملیات انجام دادهاید.
$$1 \leq r_i \leq n$$
$$1 \leq c_i \leq m$$
# مثال
## ورودی نمونه ۱
```
1 2
```
## خروجی نمونه ۱
```
1
1 1
```
با همین یک عملیات هر دو لامپ روشن میشوند چون هر دو خاموش هستند.
## ورودی نمونه ۲
```
2 2
```
## خروجی نمونه ۲
```
4
1 1
1 2
2 1
2 2
```
اگر روی هر لامپ یک عملیات انجام دهیم هر لامپ سه بار تغییر وضعیت میدهد پس در نهایت همه لامپها روشن میشوند.