+ محدودیت زمان: ۰.۵ ثانیه
+ محدودیت حافظه: ۶۴ مگابایت
----------
دور یک میز گرد، $n$ بشقاب وجود دارد. امین برای تکمیل این میز، میخواهد کنار هر بشقاب، یک **قاشق** و یک **چنگال** قرار دهد.
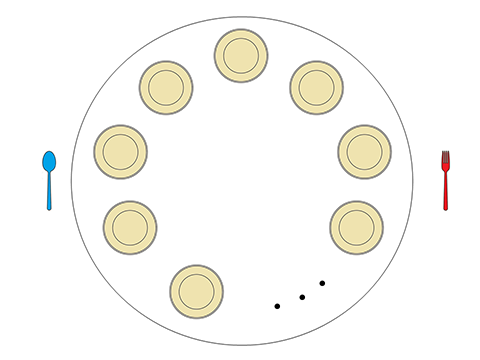
او برای اینکار، یک رشته به طول $2n$ از حروف `S` (قاشق) و `F` (چنگال) انتخاب میکند. (لزومی ندارد که تعداد حروف `F` با `S` برابر باشد.)
سپس از یکی از بشقابها شروع کرده و در جهت ساعتگرد، دور میز حرکت میکند و در مرحله $i$ام، اگر حرف $i$ام رشته، برابر `S` بود، یک قاشق و اگر `F` بود یک چنگال، کنار بشقاب مورد نظر قرار میدهد.
# ورودی
در سطر اول ورودی عدد صحیح و مثبت $n$ داده میشود.
$$1 \le n \le 100$$
در سطر دوم ورودی یک رشته به طور $2n$ از حروف `S` و `F` به شما داده میشود.
# خروجی
در تنها سطر خروجی در صورتی که کنار هر بشقاب، یک قاشق و یک چنگال قرار میگیرد، `YES` و در غیر این صورت `NO` چاپ کنید.
**توجه کنید سیستم داوری به بزرگ و کوچک بودن حروف حساس است.**
# مثالها
----------
## ورودی نمونه ۱
```
2
SFFS
```
## خروجی نمونه ۱
```
YES
```
<details class="white">
<summary>**توضیح نمونه ۱**</summary>
در تصاویر زیر، قرار گرفتن قاشقها و چنگالها را، با توجه به رشته داده شده، به صورت مرحله به مرحله میبینید.
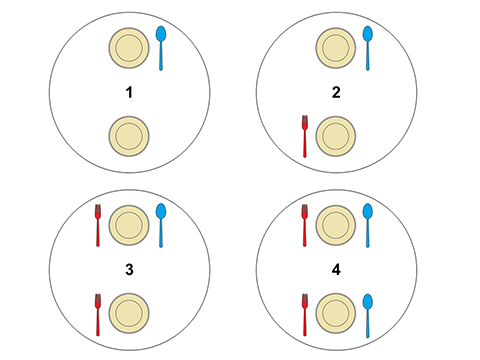
</details>
----------
## ورودی نمونه ۲
```
2
SFSF
```
## خروجی نمونه ۲
```
NO
```
<details class="white">
<summary>**توضیح نمونه ۲**</summary>
در تصاویر زیر، قرار گرفتن قاشقها و چنگالها را، با توجه به رشته داده شده، به صورت مرحله به مرحله میبینید.
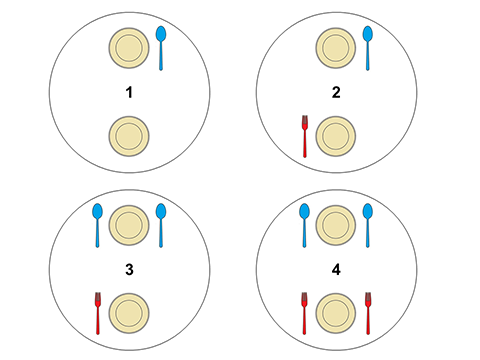
</details>
----------
## ورودی نمونه ۳
```
3
SSSSFF
```
## خروجی نمونه ۳
```
NO
```
<details class="white">
<summary>**توضیح نمونه ۳**</summary>
در تصاویر زیر، قرار گرفتن قاشقها و چنگالها را، با توجه به رشته داده شده، به صورت مرحله به مرحله میبینید.
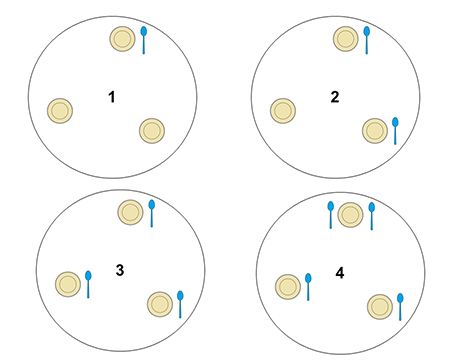
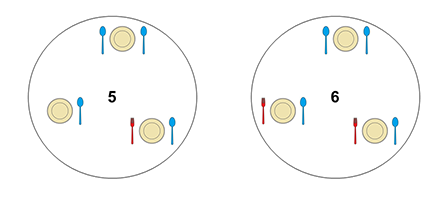
</details>
----------
## ورودی نمونه ۴
```
4
FSFFSFSS
```
## خروجی نمونه ۴
```
YES
```
<details class="white">
<summary>**توضیح نمونه ۴**</summary>
در تصاویر زیر، قرار گرفتن قاشقها و چنگالها را، با توجه به رشته داده شده، به صورت مرحله به مرحله میبینید.
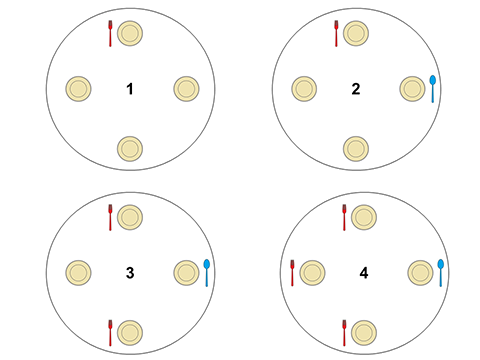
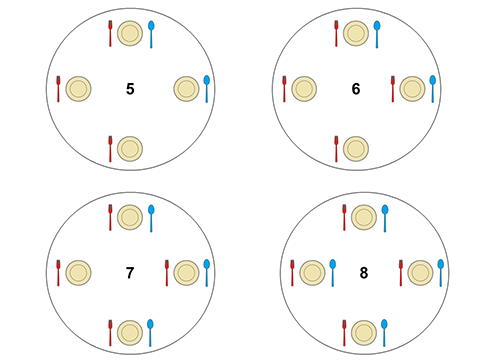
</details>
+ محدودیت زمان: ۰.۵ ثانیه
+ محدودیت حافظه: ۶۴ مگابایت
----------
یک دستگاه خودپرداز داریم که روی آن ۱۰ دکمه برای وارد کردن **هر رقم** و یک دکمه برای **پاک کردن** سمت راستترین رقم عدد وارد شده، وجود دارد.
میخواهیم با این دستگاه، عدد $n$ را وارد کنیم. اما میدانیم ۱۰ دکمه ارقام این دستگاه خراب است ولی دکمه پاک کردن، به درستی کار میکند.

ما مشکل دستگاه را فهمیدهایم و میدانیم اگر دکمه رقم $d$ وارد شود، رشته $s_d$ (به همان ترتیب) وارد دستگاه میشود. همچنین مطمئن هستیم که رقم اول رشته $s_d$ خود $d$ است. ممکن است $s_d$ شامل رقم تکراری باشد.
حال از شما میخواهیم کمترین تعداد فشار دادن دکمهها که برای وارد کردن عدد $n$ لازم است را محاسبه کنید.
# ورودی
در سطر اول ورودی عدد صحیح و مثبت $n$ داده میشود.
$$1 \leq n \leq 10^{1000}$$
در ۱۰ سطر بعدی در سطر $d$ام رشته $s_d$ آمده است.
$$ 1 \leq |s_d| \leq 10$$
تضمین میشود که رقم اول $s_d$ خود $d$ است ولی ممکن است $s_d$ رقم تکراری داشته باشد.
# خروجی
در تنها سطر خروجی، کمینه تعداد عملیات لازم برای وارد کردن عدد $n$ را بنویسید.
# مثالها
----------
## ورودی نمونه ۱
```
140102
0
1
2
3
4
5
6
7
8
9
```
## خروجی نمونه ۱
```
6
```
<details class="white">
<summary>**توضیح نمونه ۱**</summary>
دستگاه خودپرداز بالا سالم است. یعنی با فشار دادن دکمه هر رقم، فقط همان رقم نوشته میشود؛ پس کافی است برای نوشتن عدد $140102$ به صورت زیر عمل کنیم.
+ **عملیات اول.** قبل از انجام این عملیات، هیچ رقمی وارد دستگاه نشده است، پس با فشار دادن دکمه `1`، عدد $1$ وارد دستگاه میشود.
+ **عملیات دوم.** تا قبل از این عملیات عدد $1$، وارد شده است. در این عملیات با فشار دادن دکمه `4`، عدد $14$ وارد دستگاه میشود.
+ **عملیات سوم.** تا قبل از این عملیات عدد $14$، وارد شده است. در این عملیات با فشار دادن دکمه `0`، عدد $140$ وارد دستگاه میشود.
+ **عملیات چهارم.** تا قبل از این عملیات عدد $140$، وارد شده است. در این عملیات با فشار دادن دکمه `1`، عدد $1401$ وارد دستگاه میشود.
+ **عملیات پنجم.** تا قبل از این عملیات عدد $1401$، وارد شده است. در این عملیات با فشار دادن دکمه `0`، عدد $14010$ وارد دستگاه میشود.
+ **عملیات ششم.** تا قبل از این عملیات عدد $14010$، وارد شده است. در این عملیات با فشار دادن دکمه `2`، عدد $140102$ وارد دستگاه میشود.
</details>
----------
## ورودی نمونه ۲
```
18415
0
15
2
3
415
59
6
7
84
9
```
## خروجی نمونه ۲
```
4
```
<details class="white">
<summary>**توضیح نمونه ۲**</summary>
دستگاه فوق خراب است. برای وارد کردن عدد $18415$ با کمترین تعداد عملیات میتوانیم به صورت زیر عمل کنیم.
+ **عملیات اول.** قبل از انجام این عملیات، هیچ رقمی وارد دستگاه نشده است، پس با فشار دادن دکمه `1`، عدد $15$ وارد دستگاه میشود.
+ **عملیات دوم.** تا قبل از این عملیات عدد $15$، وارد شده است. در این عملیات با پاک کردن آخرین رقم، عدد وارد شده به $1$ تغییر میکند.
+ **عملیات سوم.** تا قبل از این عملیات عدد $1$، وارد شده است. در این عملیات با فشار دادن دکمه `8`، عدد $184$ وارد دستگاه میشود.
+ **عملیات چهارم.** تا قبل از این عملیات عدد $184$، وارد شده است. در این عملیات با فشار دادن دکمه `1`، عدد $18415$ وارد دستگاه میشود.
</details>
----------
## ورودی نمونه ۳
```
18415
0
16
2
3
415
59
6
7
84
9
```
## خروجی نمونه ۳
```
5
```
<details class="white">
<summary>**توضیح نمونه ۳**</summary>
دستگاه فوق خراب است. برای وارد کردن عدد $18415$ با کمترین تعداد عملیات میتوانیم به صورت زیر عمل کنیم.
+ **عملیات اول.** قبل از انجام این عملیات، هیچ رقمی وارد دستگاه نشده است، پس با فشار دادن دکمه `1`، عدد $16$ وارد دستگاه میشود.
+ **عملیات دوم.** تا قبل از این عملیات عدد $16$، وارد شده است. در این عملیات با پاک کردن آخرین رقم، عدد وارد شده به $1$ تغییر میکند.
+ **عملیات سوم.** تا قبل از این عملیات عدد $1$، وارد شده است. در این عملیات با فشار دادن دکمه `8`، عدد $184$ وارد دستگاه میشود.
+ **عملیات چهارم.** تا قبل از این عملیات عدد $184$، وارد شده است. در این عملیات با پاک کردن آخرین رقم، عدد وارد شده به $18$ تغییر میکند.
+ **عملیات پنجم.** تا قبل از این عملیات عدد $184$، وارد شده است. در این عملیات با فشار دادن دکمه `4`، عدد $18415$ وارد دستگاه میشود.
</details>
+ محدودیت زمان: ۱.۵ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
یک سالن سینما داریم که صندلیهای آن به شکل یه جدول $n \times m$ است که دارای $n$ ردیف و $m$ ستون است. ردیفها از بالا به پایین با اعداد $1$ تا $n$، و ستونها از چپ به راست با اعداد $1$ تا $m$، شمارهگذاری شده است. برخی از صندلیها با تماشاچی پر شده و برخی خالی است.
هر بار که یک تماشاچی وارد سالن میشود، به دلیل شیوع کرونا، میخواهد روی صندلیای بنشیند که نزدیکترین تماشاچی **همردیف** آن، از چپ و راست؛ بیشترین فاصله را داشته باشد. اگر هیچ تماشاچی در یک ردیف نباشد، فاصله نزدیکترین تماشاچی به این صندلی را بینهایت در نظر بگیرید.
اگر چند صندلی با این ویژگی وجود دارد صندلی که شماره سطر آن کمینه باشد و اگر چند صندلی با این ویژگی در یک سطر وجود دارد، صندلی که شماره ستون آن کمینه است، الویت دارد.
حال وضعیت اولیه نشستن تماشاچیها به شما داده میشود و از شما میخواهیم جای نشستن $k$ نفر بعدی را مشخص کنید. توجه کنید این $k$ نفر یکی یکی وارد شده و تا نشستن نفر قبلی منتظر میمانند.
# ورودی
در سطر اول ورودی سه عدد صحیح و مثبت $n$، $m$ و $k$ که با یک فاصله از هم جدا شدهاند آمده است. که به ترتیب نشاندهندهی تعداد ردیفها و ستونهای سالن و تعداد تماشاچیهایی است که میخواهند وارد سالن شوند.
$$ 1 \leq n, m \leq 1000$$
$$1 \leq k \leq \min \{ n.m,100 \, 000 \}$$
تضمین میشود که حداقل $k$ صندلی خالی در سالن سینما وجود دارد.
در $n$ سطر بعدی در هر سطر $m$ کاراکتر آمده که کاراکتر $j$ام آمده در سطر $i$ام، وضعیت صندلی سطر $i$ و ستون $j$ را نشان میدهد. اگر این کاراکتر برابر `.` باشد یعنی این صندلی خالی است و اگر `#` باشد یعنی این صندلی پر شده است.
# خروجی
اگر $k$ تعداد تماشاچیهایی که میخواهند وارد سالن شوند، باشد. خروجی $k$ سطر دارد و در سطر $i$ام دو عدد $r_i$ و $c_i$ که با یک فاصله از هم جداشدهاند، چاپ کنید که نشاندهندهی شماره سطر و ستون صندلی است که تماشاچی $i$ام روی آن مینشیند.
# مثالها
----------
## ورودی نمونه ۱
```
2 2 2
..
#.
```
## خروجی نمونه ۱
```
1 1
1 2
```
<details class="white">
<summary>**توضیح نمونه ۱**</summary>
مراحل نشستن این ۲ تماشاچی به ترتیب از چپ به راست نشان داده میشود.
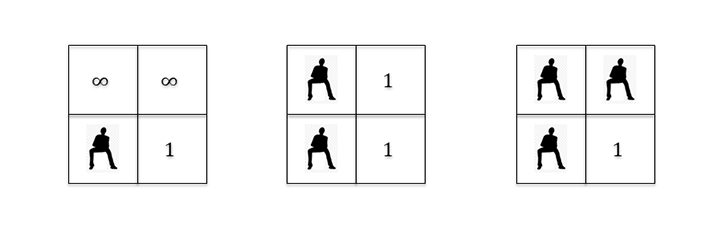
</details>
----------
## ورودی نمونه ۲
```
3 5 11
...##
#...#
.....
```
## خروجی نمونه ۲
```
3 1
3 5
1 1
2 3
3 3
1 2
1 3
2 2
2 4
3 2
3 4
```
<details class="white">
<summary>**توضیح نمونه ۲**</summary>
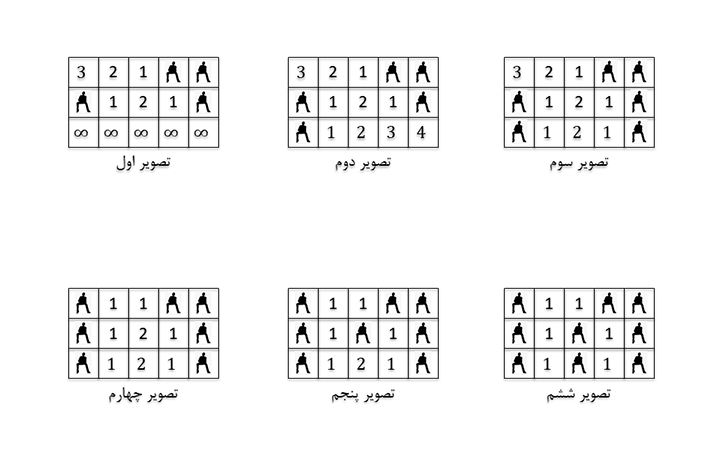
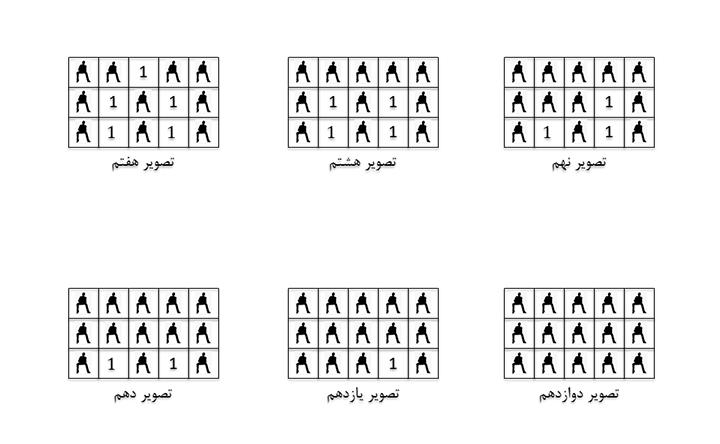
</details>
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
یک دنباله مثل $a_1, a_2, \dots, a_n \,$ «هندسیوار» میگوییم اگر برای هر $n \geq 3$ داشته باشیم:
$${a_{n - 1}}^2 = a_{n} \times a_{n - 2}$$
همه دنبالههای به طول ۱ و ۲ «هندسیوار» هستند.
به یک مستطیل «جذابوار» میگوییم اگر هر سطر آن از چپ به راست و هر ستون آن از پایین به بالا یک دنباله «هندسیوار» باشد.
یک جدول $n \times m$ داریم میخواهیم بزرگترین زیر مستطیلی از آن را پیدا کنیم که «جذابوار» باشد.
# ورودی
در سطر اول ورودی عدد صحیح و مثبت $n$ و $m$ که با یک فاصله از هم جداشدهاند آمده.
$$1 \leq n, m \leq 1000$$
در $n$ سطر بعدی در هر سطر $m$ عدد صحیح و مثبت که با یک فاصله از هم جداشده آمده است.
$$1 \leq a_{i, j} \leq 10^9$$
# خروجی
در تنها سطر خروجی مساحت بزرگترین زیرمستطیل «جذابوار» را چاپ کنید.
# مثالها
----------
## ورودی نمونه ۱
```
3 3
1 1 1
4 6 9
1 1 2
```
## خروجی نمونه ۱
```
6
```
<details class="white">
<summary>**توضیح نمونه ۱**</summary>
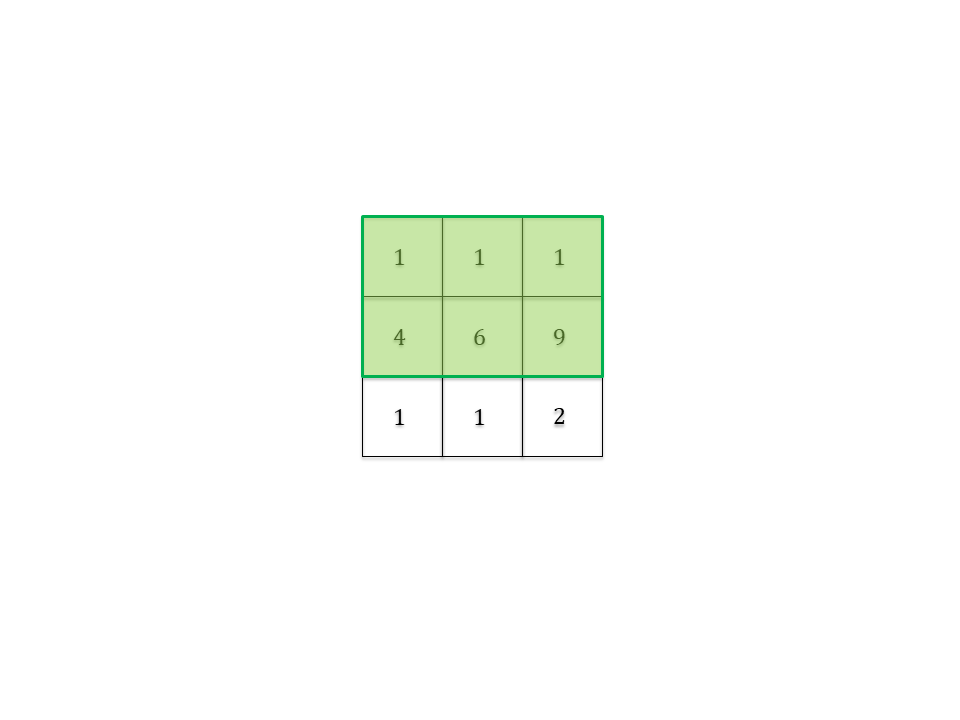
</details>
----------
## ورودی نمونه ۲
```
2 5
1 1 2 1 1
2 2 1 2 2
```
## خروجی نمونه ۲
```
4
```
<details class="white">
<summary>**توضیح نمونه ۲**</summary>
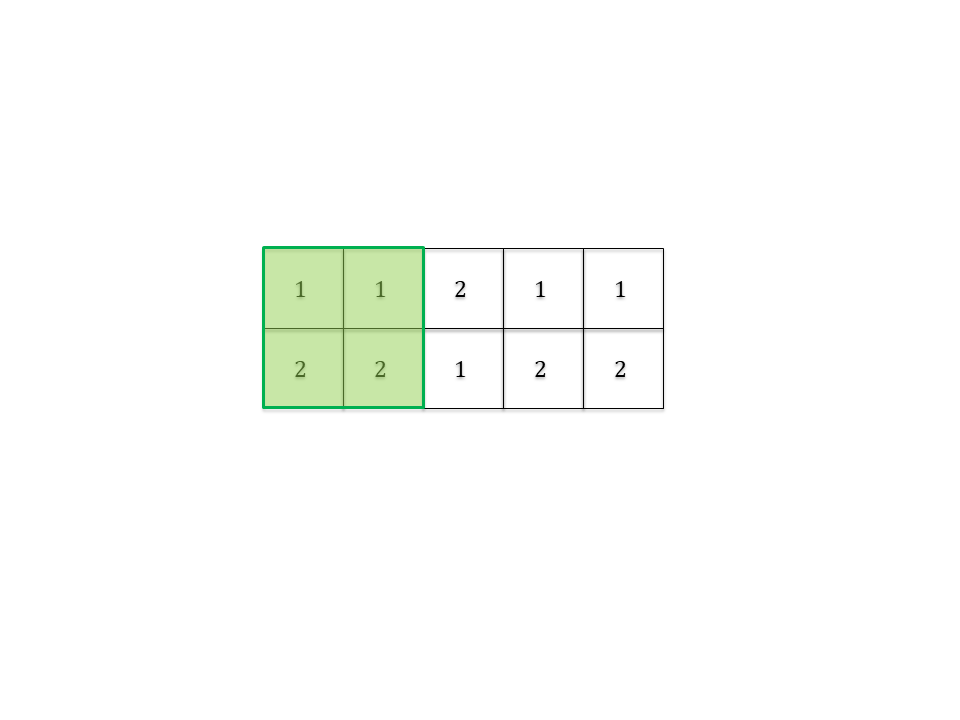
</details>
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
روی تخته $n$ عدد صحیح و مثبت $a_1, a_2, a_3, \dots, a_n \,$ نوشته شده است. در هر مرحله میتوانیم دو عدد از این دنباله را پاک کنیم و سپس ضرب یا جمع آنها را روی تخته بنویسیم.
میخواهیم این کار را طوری انجام دهیم که بعد از $n - 1$ مرحله، عددی که روی تخته باقی میماند بیشینه باشد.
با توجه به اینکه این عدد ممکن است خیلی بزرگ باشد از شما میخواهیم باقیمانده آن بر $10^9+7$ را محاسبه کنید.
# ورودی
در سطر اول ورودی عدد صحیح و مثبت $n$ آمده که نشاندهندهی تعداد اعداد نوشته شده روی تخته است.
$$1 \leq n \leq 100 \, 000$$
در سطر دوم ورودی $n$ عدد صحیح و مثبت $a_1, a_2, \dots, a_n \,$ که با یک فاصله از هم جدا شدهاند آمده است که نشاندهندهی اعداد نوشته شده روی تخته است.
$$1 \leq a_i \leq 10^9$$
# خروجی
در تنها سطر خروجی باقیمانده بزرگترین عددی که میتوان به آن رسید بر $10^9+7$ را چاپ کنید.
# مثالها
----------
## ورودی نمونه ۱
```
3
1 2 3
```
## خروجی نمونه ۱
```
9
```
----------
## ورودی نمونه ۲
```
4
1 1 1 1
```
## خروجی نمونه ۲
```
4
```