* محدودیت زمان:‌ ۱ ثانیه * محدودیت حافظه: ۲۵۶ مگابایت ------------------------------ مولین که به دنبال موجودات افسانه‌ای می‌گردد پا به سرزمین‌های خطرناک گذاشته و اکنون در وسط کویر مصر گیر افتاده‌است. او دیگر از نجات پیدا کردن نا امید شده بود که ناگهان یک کوتوله‌ی سبز رنگ او را پیدا می‌کند! کوتوله به او می‌گوید که می‌تواند یا جادوی خود او را به خانه منتقل کند ولی در صورتی این کار را می‌کند که مولین مساله زیر را برای او حل کند. یک جدول $n \times m$ به شما داده می‌شود که در تقاطع سطر $i$ ام و ستون $j$ ام $a_{i,j}$ نوشته شده است. به چند طریق می‌توان برای هر سطر و هر ستون عددی طبیعی انتخاب کرد به طوری که عدد هر خانه برابر با حاصل ضرب عدد سطر آن در ستون آن باشد؟ مولین که مهارت مثال نزدنی‌ای در سوال‌های المپیاد کامپیوتر دارد فورا مساله را حل کرده و به کمک جادو به خانه اش بر‌می‌گردد. او پس از برگشت به خانه این سوال را برای امتحان برنزکات پیشنهاد می‌دهد. اکنون وظیفه شما است که این مساله را حل کنید. # ورودی در خط اول ورودی دو عدد $ n $ و $ m $ آمده است که به ترتیب تعداد سطرها و ستون‌ها را نشان می‌دهد. در هر یک از $ n $ خط بعدی $ m $ عدد آمده که $ j $ امین عدد در خط $ i $ ام نشان‌دهنده عدد داخل خانه سطر $ i $ ام و ستون $ j $ ام جدول است. $$1 \le n, m \le 1\ 000$$ $$1 \le a_{i,j} \le 10^{12}$$ # خروجی در تنها خط خروجی, جواب مساله را چاپ کنید. # زیرمسئله‌ها | زیرمسئله | نمره | محدودیت | |:-------:|:----------:|:-----------:| |۱|۷ |$n=m=1$ | |۲ |۱۱ | $a_i \le 2$ | |۳|۴۵ |$a_i \le 1\ 000$| |۴|۳۷|بدون محدودیت اضافی| # مثال ## ورودی نمونه ۱ ``` 2 3 2 6 6 6 18 18 ``` ## خروجی نمونه ۱ ``` 2 ```

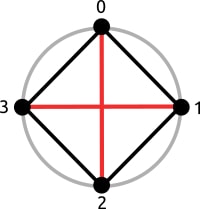
* محدودیت زمان:‌ ۱ ثانیه * محدودیت حافظه: ۲۵۶ مگابایت ------------------------------ کشور هیتایوتا از $ n $ شهر با شماره‌های $ 0 $ تا $ n - 1 $ تشکیل شده و جاده‌های آن به شکل یک $ n $ ضلعی منتظم است. پادشاه برای رفاه حال مردم $ m $ جاده دیگر ساخته است تا مردم بتوانند از این $ n + m $ جاده برای رفت و آمد خود استفاده کنند. (هر جاده دو شهر را با یک خط صاف به هم دیگر وصل می‌کند.)  پادشاه خیلی زود متوجه شد که نگه‌داری از این جاده‌ها کار بسیار هزینه‌بری است. برای همین او می‌خواهد تعدادی از جاده‌ها را خراب کند به صورتی که برای جاده‌های باقی‌مانده دو خاصیت زیر برقرار باشد: + بین هر دو شهر دقیقا یک مسیر وجود داشته باشد. + هیچ دو جاده‌ای یک‌دیگر را (جز در نقطه شروع و پایان) قطع نکنند. پادشاه می‌خواد بداند با محدودیت‌های بالا به چند روش می‌تواند جاده‌ها را خراب کند. دو روش متفاوت است اگر و تنها اگر جاده‌ای وجود داشته باشد که در یکی از آن‌ها خراب شده باشد و در دیگری خراب نشده باشد. از آن‌جایی که این عدد می‌تواند خیلی بزرگ باشد پادشاه می‌خواد بداند باقی‌مانده تقسیم این عدد بر $10^9 + 7$ چند است. # ورودی در خط اول ورودی دو عدد $ n $ و $ m $ آمده است که تعداد شهرها و تعداد جاده‌های اضافه شده را نشان می‌دهد. در $ m $ خط بعدی در هر خط دو عدد $ u $ و $ v $ آمده است که نشان‌دهنده جاده‌ای بین شهر $ u $ و $ v $ است. $$ 3 \le n \le 200$$ $$0 \le m \le \frac{n \times (n-3)}{2}$$ $$0 \le u_i, v_i \le n-1$$ بین هر دو شهر حداکثر یک جاده (از بین $ n + m $ جاده) وجود دارد و هیچ جاده‌ای یک شهر را به خودش وصل نمی‌کند. # خروجی در تنها خط خروجی، عدد مورد نظر پادشاه را چاپ کنید. # زیرمسئله‌ها | زیرمسئله | نمره | محدودیت |:------------------:|:----------:|:------------------:| | ۱ | ۱۳ | $ n \le 7 $ | | ۲ | ۲۱ | یک سر جاده‌های اضافه شده، شهر با شماره $0$ است. | | ۳ | ۶۶ | بدون محدودیت اضافی | # مثال ## ورودی نمونه ``` 4 2 0 2 1 3 ``` ## خروجی نمونه ``` 12 ```

* محدودیت زمان:‌ ۱ ثانیه * محدودیت حافظه: ۲۵۶ مگابایت ---------- اشکان برای سرگرم کردن پرهام یک بازی طراحی کرده‌است. او به پرهام یک جایگشت از اعداد صفر تا $n-1$ می‌دهد و از او می‌خواهد که با کمترین تعداد حرکت این جایگشت را مرتب کند. پرهام در هر نوبت می‌تواند جایگشت را به دو زیردنباله $S_1$ و $S_2$ افراز کند و جایگشت جدید را از کنار هم گذاشتن $S_1$ و $S_2$ به دست آورد. برای مثال او می‌تواند در یک نوبت جایگشت $<1, 3, 2, 0, 4, 5>$ را به دو زیردنباله $<3, 0, 4, 5>$ و $<1, 2>$ افراز کند و سپس به جایگشت $<3, 0, 4, 5, 1, 2>$ تبدیل کند. توجه کنید که اعضای زیردنباله به همان ترتیبی که در جایگشت هستند باید قرار گیرند، مثلا $<3, 4, 0>$ زیردنباله معتبری از جایگشت داده شده **نیست**. به پرهام کمک کنید که با کمترین تعداد حرکت جایگشت داده شده را مرتب کند. $$1 \le n \le 100\ 000$$ $$0 \le p_i \le n-1$$ # ورودی در خط اول ورودی عدد $ n $ آمده است. در خط بعد $n$ عدد $ p_0, p_1, ... , p_{n-1} $ آمده که اعداد جایگشت هستند. # خروجی در خط اول خروجی $k$، کمترین تعداد حرکت‌ مورد نیاز را چاپ کنید. در هر یک $ k + 1 $ خط بعدی $ n $ عدد چاپ کنید که خط اول خود جایگشت ورودی و پس از آن در هر خط جایگشتی که از روی جایگشت قبلی‌اش به دست می‌آید را چاپ کنید. اگر بیش از یک روش برای مرتب کردن جایگشت با کمترین تعداد حرکت وجود داشته‌باشد می‌توانید هر کدام را به دلخواه چاپ کنید. # زیرمسئله‌ها | زیرمسئله | نمره | محدودیت | |:-------:|:----------:|:-----------:| |۱ | ۱۱ | $n \le 7$ | |۲| ۲۳ | جایگشت نزولی است ($p_i > p_{i+1}$) و $n$ توانی از دو است یعنی $n=2^k$ | |۳|۴۶ | $n \le 100$| |۴|۲۰|بدون محدودیت اضافی| # مثال ## ورودی نمونه ۱ ``` 3 0 1 2 ``` ## خروجی نمونه ۱ ``` 0 0 1 2 ``` ## ورودی نمونه ۲ ``` 5 0 3 1 2 4 ``` ## خروجی نمونه ۲ ``` 1 0 3 1 2 4 0 1 2 3 4 ``` ## ورودی نمونه ۳ ``` 6 1 3 2 0 4 5 ``` ## خروجی نمونه ۳ ``` 2 1 3 2 0 4 5 3 0 4 5 1 2 0 1 2 3 4 5 ```