+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
*In 16th century Naples, a Galette flatbread was referred to as a pizza. Known as the dish for poor people, it was sold in the street and was not considered a kitchen recipe for a long time. This was later replaced by oil, tomatoes (after Europeans came into contact with the Americas) or fish. An often recounted story holds that on 11 June 1889, to honour the Queen consort of Italy, Margherita of Savoy, the Neapolitan pizza-maker Raffaele Esposito created the "Pizza Margherita", a pizza garnished with tomatoes, mozzarella, and basil, to represent the national colours of Italy as on the Italian flag.*
Ehsan and Yasaman usually eat very much and can eat a whole small pizza each in normal
occasions. They only have one rule which is that they “never share Pizza” with anyone. Now
imagine how hungry they are after a five hours ACM contest. After a five hour contest they need to eat as quickly as possible, so they usually decide to order one giant pizza instead of several small ones and forget about their “never share Pizza” rule. They wonder whether it is possible to put the big rectangular pizza on the surface of the round table such that it does not overhang the border of the table. Since they are so hungry and knocked out, your job is to write a program that helps them!
# ورودی
The first line of input shows the number of test cases $T$.
$$1 \leq T \leq 100$$
Each of following $T$ lines contains three space separated integers $r, w, l$ indicating radius of table, width and length of the pizza.
$$ 1 \leq r, w, l \leq 1000 $$
# خروجی
For each test case you should print a line indicating whether the pizza overhangs the table or not. If the pizza overhangs the border of the table, you should print `Pizza does not fit on the
table.`, otherwise print `Pizza fits on the table.`.
# مثالها
## ورودی نمونه ۱
```
3
38 40 60
35 30 70
50 60 80
```
## خروجی نمونه ۱
```
Pizza fits on the table.
Pizza does not fit on the table.
Pizza fits on the table.
```
A – Donuts and the Giant Pizza
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
+ *Good. You got that too.*
+ *Beats like digits. Every beat is a one, every rest is a zero. Binary code. That's why all those assassins tried to save my life. It was hidden on me, hidden inside my head. A few simple lines of computer code that can break into any system.*
+ *Told all my clients, last one to Sherlock is a sissy.*
+ *I can kill Rich Brook and bring back Jim Moriarty.”*

Shamir0xe, believes in binary numbers. After lots of sleepless nights, he managed to crack
Moriarty’s magical binary number to help Sherlock beat Moriarty. He realized it’s not a unique
number, every number that follows at least two of the following rules, is a magical binary number:
+ number is palindrome in decimal presentation
+ number is palindrome in hexadecimal presentation
+ number is palindrome in binary presentation
a word, phrase, or sequence that reads the same backward as forward, e.g., madam or nurses
run. ex: “abcba” is palindrome while “abcca” is not.
Your job is to help sherlock determine if a number is a magical binary number or not.
# ورودی
The first line of input shows the number of test cases $T$.
$$ 1 \leq T \leq 100$$
Each of following $T$ lines contains an integer $N$.
$$1 \leq N \leq 1000$$
# خروجی
For each test case, if the number is a magical binary number print `Magical`, otherwise print `I’m sorry Sherlock :(`.
# مثالها
## ورودی نمونه ۱
```
3
85
17
12
```
## خروجی نمونه ۱
```
Magical
Magical
I'm sorry Sherlock :(
```
In the first test case:
+ $85 = (1010101)_2 \to \text{Palindrome}$
+ $85 = (55)_{16} \to \text{Palindrome}$
B – 0x55
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
Colonelmo and CaptainH1 were hanging out at Cluna when they noticed something strange.
Cluna allows the customers to pay by credit card in a super secure way: The guy at the counter simply asks about your card's password. And if that isn't enough, he will shout it out as loud as possible after he hears it from you.
We know that there are $N$ people who are going to Cluna today, and the $i$-th person's credit card password is equal to $a_i,$ a $4$ digit number (possibly containing leading zeroes). We know that the people pay (and therefore tell their password) when they are about to leave the shop. We also have the customers' entrance/exit times. Since the guy at the counter repeats the password in a really loud voice, everybody present in the shop at that particular moment will hear it. A customer can memorize a password if and only if she is present at the shop while the cashier is shouting it and the password which is being told is similar to his own password. Two passwords are said to be similar if and only if one is a rearrangement of the digits of the other one ($1234$ is similar to say, $1234$ and $4132$ etc.).
As always, CaptainH1 is quite concerned about security matters. She asks Colonel, how many
passwords that belong to other people are known to each of the customers at the end? Colonel is too busy browsing 9gag and knows that CaptainH1 won't give him his kindersurprise if he doesn't answer in time. Can you help him?
# ورودی
The first line of input contains an integer $N$ and in the next line $N$ space separated Integers $a_1, a_2, \dots, a_N$.
$$ 1 \leq N \leq 2000$$
Next line contains an integer $M$ indicating total number of entrances/exists that have happened ordered by the time of happening.
$$ 0 \leq M \leq 2000$$
Each of following $M$ lines contains an integer $X$ denoting person $X$ will enter the shop if she is not in the shop, or otherwise she will pay and leave the shop.
$$ 1 \leq X \leq N$$
+ The same person can go to Cluna multiple times.
+ Initially there are no customers in Cluna.
# خروجی
Print $N$ space separated numbers $b_1, b_2, \dots , b_N$ each denoting the number of other people whose password is known to $i$-th person.
# مثالها
## ورودی نمونه ۱
```
5
1234 4321 2345 3455 5345
10
1
2
2
4
5
4
5
3
1
1
```
## خروجی نمونه ۱
```
1 0 0 0 1
```
+ Person one knows about person two's password.
+ Person five knows about person four's password.
C – Colonelmo, CaptainH1 and Cluna
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
Minions have been on this planet far longer than we have. They're all different. But they all share the same goal. To serve the most despicable master they could find. After thousands of rough years, finally they found the most despicable master in the world, “Erfan.aa”. They are very happy so they’re having a celebration. After dancing, singing and all of those “heavy rejections”, the time for lunch has come. The great Minion “Sir Kevin” is very creative. He and $8$ other minions form a $3\times3$ grid waiting for Erfan to bring them bananas. The grid is shown in the following picture. Each circle indicates a cell.
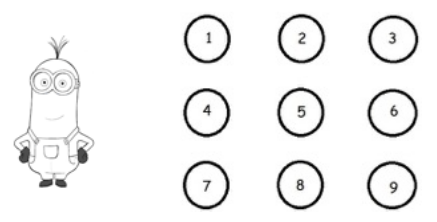
Erfan has $N$ bananas. He will start from a cell on the grid and give a banana to the Minion on that cell and go to another cell, give another banana to the Minion on the new cell and so on... until he runs out of bananas. His movement among cells must obey the following rules:
+ The line connecting the current cell to the next cell should not pass through a cell with unfed Minion
+ Each Minion must be fed at most once.
Example:
If Erfan is on the cell $7$ and The minion on the cell $4$ is fed, he can move to the following cells:
$1, 2, 5, 6, 8$
Erfan is very curious. He wants to know how many ways exist to do this task. He’s now busy in the celebration, Can you help him?
# ورودی
The first line of input shows the number of test cases $T$.
$$1 \leq T \leq 100$$
Each of following $T$ lines contains two space separated integers $S$ and $N,$ indicating start cell and number of bananas respectively.
$$ 1 \leq S, N \leq 9$$
# خروجی
For each test case, print a single line `Case#<caseNumber> : <#PossibleWays>`. For more
clarifications see Sample Output.
# مثالها
## ورودی نمونه ۱
```
4
1 2
5 2
2 1
3 3
```
## خروجی نمونه ۱
```
Case#1 : 5
Case#2 : 8
Case#3 : 1
Case#4 : 31
```
In the first test case:
There are $5$ ways to do the task:
$\{1 \to 2\},$ $\{1 \to 6\},$ $\{1 \to 5\},$ $\{1 \to 8\},$ $\{1 \to 4\}$.
D – Erfan and Minions
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
As you know, it was Valentines day just a couple of days ago and just because students of SBU are amorous, we have changed the whole statement of this problem, just for you :).
Ok, Let’s talk business. We have two groups of people each standing on a line in front of the other group playing a game. Let’s name them group A and B and let’s say group A members are all females (because ladies come first) and all group B members are males. Each person has a basket for gathering flowers (of-course from the other gender 😑 ) and lots of flowers to throw for the other group. (It’s not legal to throw flowers from baskets). Each basket have a limited capacity for collecting flowers. YES we know, this is a very lovely problem. ☺
Game is played in turns (They play simultaneously). In each turn, every person should take one of it’s beautiful and fragrant flowers and throw it in to one of his/her lovers on the other side. If a person’s basket is full, he/she leaves the stage Immediately, and perhaps going to sing the love songs in the streets…. never-mind. Though it’s a game and they all enjoy playing it, it’s a game (horror songs playing… 🎶 ) and the winner is the group exiting last. In other words, a group wins the game if there are no more members of the other group on the stage. We know both group A and group B play optimally and can communicate with each other. Shamir loves valentines and he’s busy getting prepared, So it’s up to you to decide which group will win the game…
# ورودی
The first line of input shows the number of test cases $T$. Each test case will contain $3$ lines.
$$1 \leq T \leq 100$$
The first line contains two space separated integers $N$ and $M$ indicating number of group A and group B members respectively.
$$1 \leq N, M \leq 1000$$
Second and third line will contain $N$ and $M$ space separated integers indicating initial capacity of baskets for group A and B members respectively. It’s guaranteed sum of all numbers in second and third line will not exceed $10^6$.
$$ \sum a_i + \sum b_i \leq 10^6$$
# خروجی
For each test case, print in a single line whether group `A` wins or group `B`. If no one wins print `we will all sing songs together`
# مثالها
## ورودی نمونه ۱
```
1
3 6
3 4 4
1 1 1 4 3 2
```
## خروجی نمونه ۱
```
B
```
E – Flower Lovers
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
Bob is studying at CoC university. Bob wants to make new friends. He thinks: "The friends of my friends can be my friends, too!". So if Bob and Joey are friends, and Joey and Frank are friends, then Bob and Frank can be friends, too. Bob wants to know how many people are there to be friends with. Bob is smart, Be like Bob!

# ورودی
The first line of input shows the number of test cases $T$.
$$1 \leq T \leq 100$$
Each test case starts with a line containing two space separated integers $N$ and $M$ indicating number of students and number of pairs of friends respectively.
$$1 \leq N \leq 400, \quad \quad 0 \leq M \leq 5000$$
Each of the following $M$ lines consist of two space separated integers $A$ and $B$ which indicates that person $A$ and person $B$ are friends.
$$1 \leq A \neq B \leq N$$
There might be repetitive pairs in input. Bob is always number $1$.
# خروجی
For each test case, print a single integer in a line denoting how many students are there for bob to be friends with.
# مثالها
## ورودی نمونه ۱
```
2
4 3
1 2
2 3
2 4
5 5
1 2
1 3
2 4
3 4
4 5
```
## خروجی نمونه ۱
```
2
1
```
F – Be Like Bob not Raha
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
Middle out is a compression algorithm invented by PiedPiper (a compression company) during
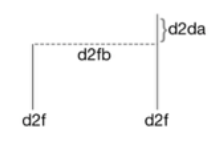
D2F calculations about how fast two agents can manipulate data with help of a third agent. Third agent is in the middle, while the other two are on two endpoints of a stream. Third agent can stay in middle if and only if it holds the D2FB (D2F Bridge) condition. D2FB condition is achieved if and only if D2DA (angle between D2Fs of agents) is smaller than D2DAT (D2DA threshold).
PiedPiper CEO just got fired and he was the only one who knew how to calculate the best
D2DAT, but since Erlich(one of PiedPiper’s board members) is the one who came up with the D2F idea, he knows about some parts of the algorithm to calculate the best D2DAT. Your job is to calculate the minimum integer value for D2DAT such that D2DB condition holds between all agents of the compression process.
Describing what D2F and D2FB are, is kinda hard, so we’re gonna use a simplified version to
show you how the algorithm works. You can suppose D2F is a tall wall, D2FB is a bridge
connecting two walls to each other and D2DA is height difference between two D2Fs.
Minimum possible value for D2DAT is the maximum D2DA between all connected agents.
# ورودی
The first line of input shows the number of test cases $T$.
$$1 \leq T \leq 30$$
Each test case starts with an integer $N$ indicating number of agents and is followed by $N+1$ lines. Next line contains $N$ space separated integers $D2F_1, D2F_2, \dots, D2F_N$ for agents. Line $i+2$’th of the test case describes connected agents to $i$’th agent.
$$1 \leq N \leq 100, \quad \quad 1 \leq D2F_i \leq 10\,000$$
each line starts with an integer $M$ and is followed by $M$ space separated integers $a_1, a_2, \dots, a_m\,\,$. $a_j$ means that agent $i$ and agent $j$ are connected to each other.
$$ 0 \leq M \leq N, \quad \quad 1 \leq a_j \leq M$$
# خروجی
For each test case, print the minimum D2DAT in a line.
# مثالها
## ورودی نمونه ۱
```
2
2
5 7
1 2
1 1
4
2 5 8 9
2 2 3
3 1 4 3
2 2 1
1 2
```
## خروجی نمونه ۱
```
2
6
```
In the first test case:
Agent one D2F has height of 5 and agent two D2F has height of 7.
Difference between them is 2 So the answer is 2.
in the second test case:
Agent one D2F has height of 2, agent two has height of 5, agent tree has height of 8 and agent four has height of 9.
+ Difference between agents one and two is 3
+ Difference between agents one and three is 6
+ Difference between agents two and four is 4
+ Difference between agents two and three is 3
So the answer is 6.
G – Middle Out
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
Ultron, the mischievous alien robot wants to attack the earth with his army and wipe out the
humans, but, everything is not going according to his plan as there are a group of superheroes
called “The Avengers” who are fighting against the alien army. Ultron knows that the avengers can take down the army and he can’t beat all of them unless he finds a way to trap them all
somewhere and kill all of them by exploding the area.
He has learned the ability of breaking and lifting a piece of land by meditation from his master but because he was never paying enough attention to his lessons (he was always dreaming about his evil plans!), he is only able to lift a square shaped piece of land. Since this trick takes a lot of energy from him, he prefers to crack the smallest possible square. Now here is the deal, he gives the position and speed of all the avengers at time “0” to you, if you give him the minimum size of square side that contains all of the avengers from now, he will let you and your laptop to happily live forever on the earth.(for simplicity, he wants the sides of squares to be aligned with Coordinate axes).
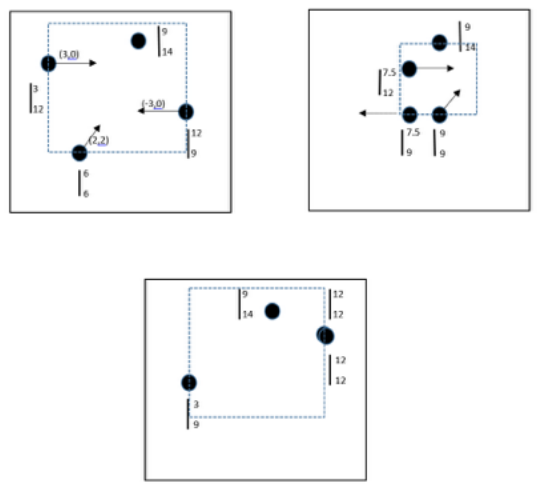
# ورودی
The first line of input shows the number of test cases $T$. Each test case contains an integer $N$ and is followed by $N$ lines.
$$1 \leq N \leq 100\,000$$
Each line consists of $4$ floating point numbers $X, Y, V_X, V_Y$ indicating starting position and speed vector of each avengers.
$$ -10\,000 \leq X , Y \leq 10\,000$$
$$ -100 \leq V_X, V_Y \leq 100$$
You can assume the maximum time is $10^9$
# خروجی
For each test case, print the minimum side of the square which all the avengers could be fitted into.
# مثالها
## ورودی نمونه ۱
```
3
4
3 12 3 0
9 14 0 0
6 6 2 2
12 9 -3 0
3
0 0 1 1
3.5 0 -1 0
0 -1 -1 -1
3
10 10 -1 -0.5
2 4 1 1
-10 15 4 -1.75
```
## خروجی نمونه ۱
```
5.00
3.50
0.00
```
H – Trap of Ultron
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
It will be the greatest event of all times, yes… you’ve guessed
right… it’s SHAMIR’S BIRTHDAY PARTYYYY!!!

But unfortunately, Shamir is very lonely and he is not in a party mood right now, poor Shamir. So he wants to invite as minimum of his friends as possible (at least one!) as long as no one gets sad. One would get sad if he/she misses someone. Yes as you’ve realized this problem is also love-related. So if Shamir invites a person, he has to invite all of his/her crushes too.
+ “what a `b****** p*** a**` ”, Shamir said.
You, as a genius programmer (like AmirShams) should help Shamir Figure it out. you will be given the crushes-list of every person that possibly can come to party. You should determine
what’s the minimum number of people Shamir should invite so that no one during the party get upset and miss some other bastards. So help Shamir! (Remember, Shamir has to invite someone)
# ورودی
The first line of input shows the number of test cases $T$.
$$1 \leq T \leq 10$$
Each test case contains two space separated integers $N$ and $M$ indicating Shamir’s friends (and their friends too) and number of crushes lists respectively and is followed by $M$ lines.
$$1 \leq N, M \leq 100 \, 000$$
Each of following $M$ lines there will be two integers $U$ and $V$ indicating $U$ has a crush over $V$.
$$1 \leq U \neq V \leq N$$
Shamir friends are weird like him. don’t care about his friends genders. so Triangle-love is possible!
# خروجی
For each test case, print the minimum number of Shamir’s friends that should come to the party so that anyone will have a good time in the party (and possibly outside the party).
# مثالها
## ورودی نمونه ۱
```
1
4 4
1 2
2 4
4 1
2 3
```
## خروجی نمونه ۱
```
1
```
I – Shamir’s Birthday Party
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
+ RRRRIIIIIING….. RRRIIIIIINNNGG….
+ Hello? Yes. Yes it's me. Okay, be there ASAP. Guys? We got a situation.
Minutes after the telephone at “The Overweight Police” (also known as “Police-e fat ha”)
headquarters rang, the officers moved out in helicopters to take care of the situation.
It's a robbery. TIGH (TIGH Infamous Group of Hackers) are disappointed in their laptops this time and have set their green-text-on-a-black-background terminals aside to attack the KFC (KFC Federal Club) building in person! $n-1$ rooms and a roof combine for $n$ occupiable places in KFC. The rooms in KFC like the ones in any other ordinary building, are uniquely numbered from $2$ to $n$. Roof is assigned the number $1$.
There are $n-1$ staircases in the building which are the only means to move from one room (or roof) to another. Each staircase connects $2$ different rooms(or a room and the roof). It is known that there exists a unique way to go from the roof to any other room in the building if you only move down the staircases (Which means the setting of the rooms and the staircases among them forms a tree).
The victim is Gigi who He has been to a party last week. Just like everybody else, Gigi took
countless pictures at they party with his sisters, mothers[citation needed], cousins, aunts and his brothers' wives. He's such a kind person that he took pictures with every single one of her $84$ daughters too (Unfortunately one of her daughters was not present at the party). As you know hackers continuously strive and plan to steal random family pictures from random people (not so random in this case. Coincidence? I guess not). TIGH is no exception. But wait! There's more! As you know “police-e fatha looks after everything”. They're not gonna let TIGH escape without a fight.
In $m$ seconds, $m$ events happen in order, each of which fits in exactly one of the following two categories:
+ A member of TIGH steals the photos in the room number $x$.
+ An overweight police jumps in the room number $y$ from the helicopter.
Hence the name, police-e fatha don't like physical activities very much. Also they are pretty
optimistic, so every time an overweight police jumps off from the helicopter into a room, she
thinks about what is the maximum number of TIGH members that she could catch if she only
used the staircases downwards considering she is “lucky”. An overweight police can catch a
TIGH member if and only if they are in the same room at some moment.
The members of TIGH are as optimistic as fatha. When they steal some photos they would try to escape through the roof (using the command “$sudo teleport” which only works in the rooftops).
Since TIGH members are not out of their minds, they will only use staircases upwards. they think to themselves what is the minimum number of fat polices that they have to escape from to reach
the rooftop considering they are “lucky”. A TIGH member has to escape from a fat police if and only if they are in the same room at some moment.
TIGH members are aware of the fact that the cops only move downwards, and the cops know
that the hackers will only move towards the roof. Please note that nobody actually moves from her initial position. They only “think” about what would happen if everybody suddenly had the ability to move (with the conditions specified above). The term “lucky” in the above statements means that everyone thinks about her own best-case scenario.
For example a lucky situation for a cop would be just waiting in his initial node, and catch every TIGH member that tries to pass him. You can prove that this strategy yields the maximum number of hackers that can be caught by the cop. For a better understanding take a look at the samples.
# ورودی
The first line of the input will consist of two numbers $n$ and $m$,
$$0 \lt n \lt 10^5, \quad \quad 0 \lt m \lt 10^5$$
then follow $n-1$ lines each of which describing a staircase in the building “from” room number $x_i$ “downward” to room number $y_i$.
The next $m$ lines are of the form “$t_i\,x_i$” where $1\leq t_i \leq 2$. $t_i = 1$ means that an overweight police is placed in the room number $x_i$ and $t_i = 2$ means that a TIGH member steals photos from the room number $x_i$.
# خروجی
Output $m$ integers in different lines, $i$th of them is the answer to the question that the person in the $i$th event asks herself.
# مثالها
## ورودی نمونه ۱
```
8 10
1 2
2 3
3 4
1 5
5 6
6 7
5 8
1 1
1 2
2 2
2 3
1 3
2 4
1 1
2 5
2 7
1 5
```
## خروجی نمونه ۱
```
0
0
1
1
1
2
3
0
0
2
```
1. No tigh member at all, therefore the answer is 0.
2. Still no tigh member.
3. A hacker and a cop are at room number 2, therefore the the hacker definitely has to escape
him. There is also a cop on the roof too but if the hacker is “lucky”, she can wait for that cop to take the staircase from 1 downward to 4 (Note that the cop can not come back up the staircases). So in the best case scenario she will only encounter the cop at room number 2.
4. no matter how lucky the hacker is, she has to get passed the second cop, because she will
only move upwards and the cop will only move downwards. Again in the best-case scenario she can avoid the first cop.
5. the cop can catch the hacker which occupies the same room with him.
6. Like the above cases, the hacker has to pass along the second and third cops no matter how well things go. Again she can avoid the first (in the input) cop.
7. If the cop is lucky, she can wait at where she is placed (roof) for all the hackers in the lower
levels. Therefore in the best-case scenario she can catch them all.
8. The hacker can avoid both of the cops at #1. (wait for both of them to go towards room #2).
9. Same as above.
10. This cop can catch the hacker which had been previously placed in room number 5. Also in the best-case scenario for him, he will wait until the hacker in the room #7 comes up the stairs and he will arrest him.