• محدودیت زمان: ۰.۵ ثانیه
• محدودیت حافظه: ۶۴ مگابایت

دارا و سارا خواهر و برادر یکدیگر هستند. در مراسم سال نو، مادربزرگ برایشان $n$ عروسک خریده است. اندازه‌ی این عروسک‌ها از $1$ تا $n$ هستند. $1$ از همه کوچک‌تر و $n$ از همه بزرگ‌تر است. این $n$ عروسک برای هر دوی آن‌ها است و قرار است باهم بازی کنند.

مادربزرگ می‌خواهد به ترتیبی آن‌ها را به دارا و سارا نشان بدهد. دارا عاشق کادوهای بزرگ و سارا عاشق کادوهای کوچک است.

• اگر دارا یک عروسک بزرگ‌تر از عروسک‌هایی که تا الان آمده است را ببیند، جیغ می‌زند.
• اگر سارا یک عروسک کوچک‌تر از عروسک‌هایی که تا الان آمده است ببیند جیغ می‌زند.

مثلاً بعد از آمدن عروسک اول، هر دوی آن‌ها جیغ می‌زنند.

مادربزرگ می‌خواهد عروسک‌ها را به ترتیبی نشان دهد که مجموع تعداد جیغ دارا و سارا کمینه شود. به مادربزرگ بگویید در بهترین ترتیب ممکن، حداقل چند جیغ را می‌شنود.

ورودی🔗

در تنها سطر ورودی، عدد صحیح و مثبت $n$ آمده که تعداد عروسک‌ها را نشان می‌دهد.

$1 \leq n \leq 100$

خروجی🔗

در تنها سطر خروجی، کمینه مجموع تعداد جیغ دارا و سارا را چاپ کنید.

مثال‌ها🔗

ورودی نمونه ۱🔗

1

خروجی نمونه ۱🔗

2

در این حالت مادر بزرگ فقط یک عروسک دارد، و با نشان دادن آن، دارا و سارا هر دو جیغ می‌زنند. پس تعداد جیغ‌ها برابر $2$ خواهد بود.

ورودی نمونه ۲🔗

2

خروجی نمونه ۲🔗

3

در این حالت مادر بزرگ می‌تواند:

• در مرحله اول عروسک، $1$ را نشان دهد و دارا و سارا با دیدن آن هر دو جیغ می‌زنند.
• در مرحله دوم عروسک، $2$ را نشان دهد و دارا با دیدن این عروسک یک جیغ می‌زند.

بنابراین مجموع جیغ‌ها $2 + 1 = 3$ خواهد بود.

ورودی نمونه ۳🔗

3

خروجی نمونه ۳🔗

3

در این حالت مادر بزرگ می‌تواند:

• در مرحله اول عروسک، $1$ را نشان دهد و دارا و سارا با دیدن آن هر دو جیغ می‌زنند.
• در مرحله دوم عروسک، $3$ را نشان دهد و دارا با دیدن این عروسک یک جیغ می‌زند.
• در مرحله سوم عروسک، $2$ را نشان دهد و هیچ کدام با دیدن آن جیغ نمی‌زنند.

بنابراین مجموع جیغ‌ها $2 + 1 + 0 = 3$ خواهد بود.

• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

«دکارتی» تردستی ماهر است. وقتی دست دکارتی از روی کارتی رد شود، کارت برعکس می‌شود. (یعنی اگر کارت رو باشد پشت می‌شود و اگر پشت باشد رو می‌شود.) آقای دکارتی می‌خواهد $t$ روز متوالی تردستی کند. در هر روز تعدادی کارت پیش روی او است و او در یک عملیات می‌تواند بازه‌ای دلخواه و متوالی از کارت‌ها را برعکس کند. او می‌خواهد حداقل تعداد عملیات که همه کارت‌ها به سمت رو تبدیل شوند را بداند!

ورودی🔗

در خط اول $t$ می‌آید که نشان دهنده تعداد روزهایی است که آقای دکارتی تردستی می‌کند. $1 \leq t \leq 1000$

در $t$ خط بعد، در هر کدام یک رشته می‌آید که حرف $i$ام آن اگر 1 باشد یعنی کارت $i$ام رو است و اگر 0 باشد یعنی کارت $i$ام به پشت قرار دارد.

تعداد کارت‌های هر روز حداکثر ۵۰ است.

خروجی🔗

در خط $i$ام از $t$ خط جواب مساله را خروجی دهید.

مثال🔗

ورودی نمونه ۱🔗

5
01
00010
11011
111000
101010101

خروجی نمونه ۱🔗

1
2
1
1
4

• در روز اول بازه‌ی $[1,1]$ را برعکس کند.
• در روز دوم بازه‌های $[4,4]$ و $[1,5]$ را برعکس کند.
• در روز سوم بازه‌ی $[3,3]$ را برعکس کند.
• در روز چهارم بازه‌ی $[4, 6]$ را برعکس کند.
• در روز پنجم بازه‌های $[2, 2]$، $[4, 4]$، $[6 ,6]$ و $[8 ,8]$ را برعکس کند.

• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

امین در کلاس درس «قضیه سیلو و نظریه گالوا» شرکت کرده است. دکتر طالب در این کلاس $n$ فایل pdf جزوه برای دانشجویان ارسال کرده است. فایل $i$ام مربوط به جلسه $i$ام است. جلسات به ترتیب تدریس شده‌اند و جزوه هر درس بلافاصله بعد از پایان آن کلاس روی سامانه قرار گرفته است. می‌دانیم امین هم جزوه هر درس را بلافاصله بعد از قرار گرفتن در سامانه دانلود کرده و در یک پوشه مخصوص جزوه‌های این درس ذخیره کرده است.

اما امین یک ابزار کارآمد دارد که این جزوات را بهم می‌چسباند و تنها دو بار از این ابزار استفاده می‌کند، یکبار برای امتحان میان ترم و یکبار برای امتحان پایان ترم.

یعنی اگر امتحان میان‌ترم بین جلسات $m$ ($1 \le m \le n - 1$) و جلسه $m + 1$ کلاس برگزار شود، امین برای درس خواندن، تمام جزوه‌های مربوط به جلسه $1$ تا $m$ را به هم می‌چسباند و یک فایل جدید درست می‌کند. (تا راحت‌تر مطالعه کند.)

همچنین امین برای امتحان پایان‌ترم، جزوه تمام $n$ جلسه را به ترتیب به هم می‌چسباند و یک فایل جدید درست می‌کند.

اکنون امین فارغ التحصیل شده ولی پوشه مربوط به جزوه‌های امین برای این درس باقی‌مانده. یعنی این پوشه شامل $n + 2$ فایل است ولی مشخص نیست که این فایل‌ها مربوط به کدام جلسات است و کدام یک فایل میان‌ترم و کدام یک فایل پایان‌ترم.

تنها چیزی که مشخص است، حجم فایل‌ها است. و می‌دانیم فایلی که از بهم چسباندن چند فایل دیگر بدست بیاید حجمش برابر مجموع حجم آن فایل‌ها خواهد بود.

حال از شما می‌خواهیم با داشتن حجم این $n + 2$ فایل، حجم جزوه میان‌ترم و پایان ترم را مشخص کنید.

ورودی🔗

در سطر اول ورودی عدد صحیح و مثبت $n$ داده می‌شود. که نشان‌دهنده‌ی تعداد جلسات تدریس است. $1 \le n \le 100 \, 000$ در سطر دوم ورودی $n + 2$ عدد صحیح و مثبت $a_1, a_2, \dots, a_{n + 2}$ آمده که حجم فایل‌های امین را نشان می‌دهد. $1 \le a_i \le 10^9$

تضمین می‌شود همواره جوابی برای این مسئله وجود دارد.

خروجی🔗

در تنها سطر خروجی دو عدد صحیح و مثبت که با فاصله از هم جداشده‌اند را چاپ کنید که عدد اول نشان‌دهنده‌ی حجم فایل میان‌ترم و عدد دوم نشان‌دهنده‌ی حجم فایل پایان‌ترم است.

مثال‌ها🔗

ورودی نمونه ۱🔗

2
11 5 6 5

خروجی نمونه ۱🔗

5 11

اگر فرض کنیم حجم فایل جلسه اول $5$ و جلسه دوم $6$ باشد و میان‌ترم بین این دو جلسه برگزار شده باشد، حجم فایل میان‌ترم $5$ و حجم فایل پایان ترم $5 + 6 = 11$ خواهد بود.

ورودی نمونه ۲🔗

6
1 2 3 6 4 5 6 21 

خروجی نمونه ۲🔗

6 21

اگر فرض کنیم، حجم فایل جلسه‌ی $k$ام برابر $k$ باشد. (برای هر $1 \leq k \leq 5$) و امتحان میان ترم بین دو جلسه‌ی سوم و چهارم برگزار شود، حجم فایل میان‌ترم برابر $1 + 2 + 3 = 6$ و پایان ترم برابر $1 + 2 + 3 + 4 + 5 + 6 = 21$ خواهد بود.

• محدودیت زمان: ۲ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

سال رو به اتمام است و شرکت کوئرا قصد دارد نمای ساختمان خود را چشم‌نواز کند. سایر شرکت‌ها هم که کوئرا الگوی آنهاست تصمیم مشابهی می‌گیرند. نمای هر ساختمان $n$ طبقه به عرض $m$ از $n\times m$ پنجره تشکیل شده یعنی نمای هر طبقه از $m$ پنجره متوالی به عرض ۱ تشکیل شده است.

حال شرکت‌ها می‌خواهند تمام پنجره‌های خود را رنگ کنند و برای رنگ‌آمیزی هر پنجره می‌توانند تنها از ۴ رنگ قرمز و آبی و سبز و زرد استفاده کنند ولی توجه کنید که هر رنگ‌آمیزی چشم‌نواز نیست و رنگ آمیزی چشم نواز است که هیچ دو پنجره همرنگی اشتراک با هم نداشته باشند! می‌گوییم دو پنجره با هم اشتراک دارند اگر حداقل یکی از ۴ گوش یک پنجره گوشه پنجره دیگر نیز باشد.

حال مدیر هر شرکت مایل است بداند چند رنگ‌آمیزی چشم‌نواز برای نمای شرکتش وجود دارد! از آنجا که ممکن است این عدد بزرگ باشد باقی‌مانده جواب بر $10^9 + 7$ را خروجی دهید.

ورودی🔗

در خط اول $t$ نشان‌دهنده تعداد شرکت‌ها می‌آید. $1 \leq t \leq 200 \, 000$ در $t$ خط بعد در هر کدام به ترتیب دو عدد $n_i$ و $m_i$ می‌آید که به ترتیب نشان دهند تعداد طبقات و عرض شرکت $i$ام است. $1 \le n_i, m_i \le 500\, 000$

خروجی🔗

در خط $i$ام از $t$ خط خروجی جواب مساله را خروجی دهید.

مثال🔗

ورودی نمونه ۱🔗

4
1 3
2 2
3 3
187563 196327

خروجی نمونه ۱🔗

36
24
72
814094109

• محدودیت زمان: ۱.۵ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

آقای هاشمی $n$ گونی خالی در یک ردیف کنار هم گذاشته است. او گونی‌ها را با اعداد $1$ تا $n$ به ترتیب از چپ به راست شماره‌گذاری کرده است.

او می‌خواهد در $m$ عملیات در این گونی‌ها مهره بریزد. او در عملیات $i$ام سه عدد $l_i$، $r_i$ و $x_i$ را انتخاب می‌کند و سپس در همه‌ی گونی‌های بازه‌ی $[l_i, r_i]$ یک مهره $x_i$ می‌اندازد.

آقای هاشمی می‌خواهد بعد از پایان این $m$ عملیات، برای هر گونی، کوچک‌ترین عددی که هیچ مهره‌ای با آن شماره در آن گونی نیست را حساب کند.

ورودی🔗

در سطر اول ورودی دو عدد صحیح $n$ و $m$ که با یک فاصله از هم جدا شده‌اند آمده است. $1 \leq n, m \leq 500 \, 000$ در $m$ سطر بعدی در هر سطر، سه عدد $l_i$، $r_i$ و $x_i$ که با یک فاصله از هم جدا شده‌اند به ترتیب می‌آیند.

$1 \leq l_i \leq r_i \leq n, \quad \quad 1 \leq x_i \leq 10^9$

خروجی🔗

در تنها سطر خروجی، $n$ عدد صحیح که با یک فاصله از هم جدا شده‌اند چاپ کنید. عدد $i$ام نشان دهنده‌ی پاسخ مسئله برای گونی $i$ام است.

مثال🔗

ورودی نمونه ۱🔗

3 2
1 2 1
2 3 2

خروجی نمونه ۱🔗

2 3 1

بعد از پایان این عملیات‌ها وضعیت مهره‌ها در هر گونی به صورت زیر است:

• گونی $1$: $\{1\}$
• گونی $2$: $\{2, 1\}$
• گونی $3$: $\{2\}$

ورودی نمونه ۲🔗

5 8
1 3 1
3 3 4
1 2 1
5 5 1
4 5 5
2 5 3
1 5 2
3 4 3

خروجی نمونه ۲🔗

3 4 5 1 4

بعد از پایان این عملیات‌ها وضعیت مهره‌ها در هر گونی به صورت زیر است:

• گونی $1$: $\{1, 1, 2\}$
• گونی $2$: $\{1, 1, 3, 2\}$
• گونی $3$: $\{1, 4, 3, 2, 3\}$
• گونی $4$: $\{5, 3, 2, 3\}$
• گونی $5$: $\{1, 5, 3, 2\}$

• محدودیت زمان: ۲ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

یک صفحه شطرنج به صورت یک جدول $n \times m$ داریم. سطرهای آن به ترتیب از بالا به پایین با اعداد $1$ تا $n$ و ستون‌های آن به ترتیب از چپ به راست با اعداد $1$ تا $m$ شماره گذاری شده است.

هر خانه از این جدول یا مانع دارد و یا آزاد است. می‌خواهیم $k$ مهره‌ی فیل در خانه‌های خالی این جدول قرار دهیم، به طوری که هیچ دو فیلی یکدیگر را تهدید نکنند. دو فیل زمانی یک دیگر را تهدید می‌کنند که یک مسیر اریب و بدون مانع بین آن‌ها موجود باشد.

از شما می‌خواهیم با دریافت وضعیت جدول، حداکثر تعداد فیلی که می‌توان در این جدول گذاشت تا هیچ دو فیلی یکدیگر را تهدید نکنند را محاسبه کنید. همچنین یک وضعیت برای قرار دادن فیل‌ها در جدول ارائه کنید. اگر چند پاسخ برای این مسئله وجود دارد، یکی را به دلخواه چاپ کنید.

ورودی🔗

در خط اول به ترتیب دو عدد $n$ و $m$ می‌آید که نشان دهنده ابعاد جدول است.

$1 \le n,m \le 400$

در $n$ خط بعد در هر خط یک رشته به طول $m$ متشکل از . و # می‌آید. اگر حرف $j$ام رشته $i$ام # باشد یعنی خانه‌ی سطر $i$ام و ستون $j$ام با مانع پر شده است و در غیر ایصورت اگر . باشد یعنی آن خانه خالی است.

خروجی🔗

در سطر اول خروجی، عدد صحیح $k$ که نشان‌دهنده‌ی حداکثر تعداد فیل است را چاپ کنید.

در $k$ سطر بعدی، در هر سطر دو عدد صحیح $r_i$ و $c_i$ که با یک فاصله از هم جدا شده‌اند و به ترتیب نشان‌دهنده‌ی شماره‌ی سطر و ستون فیل $i$ام است را چاپ کنید.

مثال‌ها🔗

ورودی نمونه ۱🔗

4 11
...#..#....
.#.##.#....
...#.##....
####..#....

خروجی نمونه ۱🔗

16
1 1
1 3
1 5
1 6
1 8
1 9
1 10
2 1
2 3
3 1
3 3
3 5
4 5
4 8
4 9
4 10

خانه‌های سفید خالی، خانه‌های سیاه مانع و خانه‌های سبز فیل هستند.

ورودی نمونه ۲🔗

10 10
.....#....
.#......#.
.#...#....
.....#....
..........
#....#.#..
.........#
#......#..
...#...#..
.....#....

خروجی نمونه ۲🔗

27
1 1
1 3
1 4
1 8
1 9
1 10
2 1
3 1
3 3
3 10
4 1
4 3
4 7
4 10
5 7
5 10
6 10
7 1
7 2
7 7
8 4
8 9
8 10
9 1
10 3
10 9
10 10

• محدودیت زمان: ۲ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

می‌خواهیم تمام نقاط صحیح محور مختصات را با $n$ رنگ متفاوت، رنگ کنیم.

می‌دانیم طول تناوب رنگ $i$ ام $l_i$ است، به این معنی که اگر هر نقطه‌ای مانند $x$ را با رنگ $i$ام رنگ کنیم، باید نقاط $x+l_i$ و $x-l_i$ نیز حتما به رنگ $i$ام باشند.

از شما خواسته شده است تا بگویید چند روش متفاوت برای این رنگ‌آمیزی وجود دارد. تضمین می‌شود با وجود اینکه تعداد نقاط صحیح محور مختصات نامتناهی است، تعداد روش‌ها متناهی خواهد بود.

از آنجایی که جواب نهایی می‌تواند بسیار بزرگ باشد، کافی است باقی مانده‌ی پاسخ را بر $10^9+7$ چاپ کنید.

ورودی🔗

در اولین خط از ورودی مقدار $n$ به شما داده شده است.

$1 \le n \le 10^6$

در خط بعدی $n$ عدد آمده است که عدد $i$ام نمایانگر مقدار $l_i$ است.

$1 \le l_i \le 10^6$

خروجی🔗

در تنها خط خروجی باید تعداد روش‌های رنگ‌آمیزی محور مختصات را چاپ کنید.

مثال🔗

ورودی نمونه ۱🔗

3
1 1 1

خروجی نمونه ۱🔗

3

ورودی نمونه ۲🔗

4
1 2 4 4

خروجی نمونه ۲🔗

26

• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

چهار ریاضی‌دان که می‌دانند از ریاضی چیزی کاسب نمی‌شوند تصمیم به جمع آوری گردو‌های روی زمین می‌گیرند! به طور مشخص زمین را صفحه مختصات دوبعدی و هرگردو را می‌توانید یک نقطه با مختصات صحیح فرض کنید. حال برای جلوگیری از دعوای احتمالی تصمیم می‌گیرند که زمین را ۴ بخش کنند که در هر بخش تعداد یکسانی گردو باشد. آنها می‌خواهند از دو خط متقاطع برای بخش‌بندی زمین استفاده کنند. برای حل حالت‌های مختلف به آنها کمک کنید $\dots$

ورودی🔗

در خط اول ورودی $t$ یا تعداد سناریوهای مختلف برای باغ گردو می‌آید. سپس در خطوط بعد $t$ تست به شرح زیر می‌آید.

$1 \leq t \leq 100$

در خط اول هر سناریو $n$ یا تعداد گردوها می‌آید و در $n$ خط بعد هر کدام دو عدد $x_i$ و $y_i$ نشان دهنده مختصات یک گردو می‌آید. تضمین می‌شود در یک سناریو دو گردو در یک نقطه نباشند. $1 \le n \le 100$ $|x_i|, |y_i| \le 10^5$

خروجی🔗

برای هر سناریو معادله دو خط را در خطوط متوالی خروجی دهید. توجه کنید نباید گردویی روی خطوط قرار بگیرد و همچنین تضمین می‌شود برای سناریوهای موجود در ورودی حتما دو خط با خاصیت گفته شده موجود است. برای خروجی خطی که معادله نظیرش $a\times x + b \times y + c = 0$ است کافی است سه عدد $a$ و $b$ و $c$ را با فاصله و به ترتیب چاپ کنید به طوری که : $|a|, |b|, |c| \le 10^9$ سه عدد خروجی می‌توانند تا ۹ رقم اعشار داشته باشند.

مثال🔗

ورودی نمونه ۱🔗

2
4
0 0
1 1
0 1
1 0
8
1 1
1 3
2 2
2 3
3 1
3 3
4 1
4 2

خروجی نمونه ۱🔗

0.000 1.000 -0.500
1.000 0.000 -0.500
0.200 1.000 -2.500
1.000 0.000 -2.500

تصویر سناریو اول:

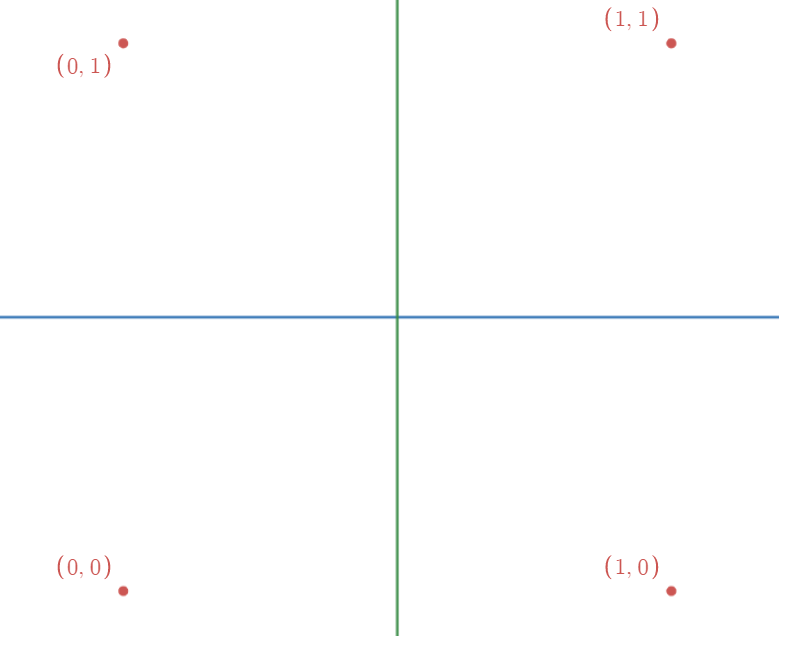
تصویر سناریو دوم: