+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
چهار ریاضیدان که میدانند از ریاضی چیزی کاسب نمیشوند تصمیم به جمع آوری گردوهای روی زمین میگیرند! به طور مشخص زمین را صفحه مختصات دوبعدی و هرگردو را میتوانید یک نقطه با مختصات صحیح فرض کنید. حال برای جلوگیری از دعوای احتمالی تصمیم میگیرند که زمین را ۴ بخش کنند که در هر بخش تعداد یکسانی گردو باشد. آنها میخواهند از دو خط متقاطع برای بخشبندی زمین استفاده کنند. برای حل حالتهای مختلف به آنها کمک کنید $\dots$
# ورودی
در خط اول ورودی $t$ یا تعداد سناریوهای مختلف برای باغ گردو میآید. سپس در خطوط بعد $t$ تست به شرح زیر میآید.
$$1 \leq t \leq 100$$
در خط اول هر سناریو $n$ یا تعداد گردوها میآید و در $n$ خط بعد هر کدام دو عدد $x_i$ و $y_i$ نشان دهنده مختصات یک گردو میآید. تضمین میشود در یک سناریو دو گردو در یک نقطه نباشند.
$$ 1 \le n \le 100$$
$$ |x_i|, |y_i| \le 10^5 $$
# خروجی
برای هر سناریو معادله دو خط را در خطوط متوالی خروجی دهید. **توجه کنید نباید گردویی روی خطوط قرار بگیرد و همچنین تضمین میشود برای سناریوهای موجود در ورودی حتما دو خط با خاصیت گفته شده موجود است.**
برای خروجی خطی که معادله نظیرش $a\times x + b \times y + c = 0$ است کافی است سه عدد $a$ و $b$ و $c$ را با فاصله و به ترتیب چاپ کنید به طوری که :
$$ |a|, |b|, |c| \le 10^9$$
سه عدد خروجی میتوانند تا ۹ رقم اعشار داشته باشند.
# مثال
## ورودی نمونه ۱
```
2
4
0 0
1 1
0 1
1 0
8
1 1
1 3
2 2
2 3
3 1
3 3
4 1
4 2
```
## خروجی نمونه ۱
```
0.000 1.000 -0.500
1.000 0.000 -0.500
0.200 1.000 -2.500
1.000 0.000 -2.500
```
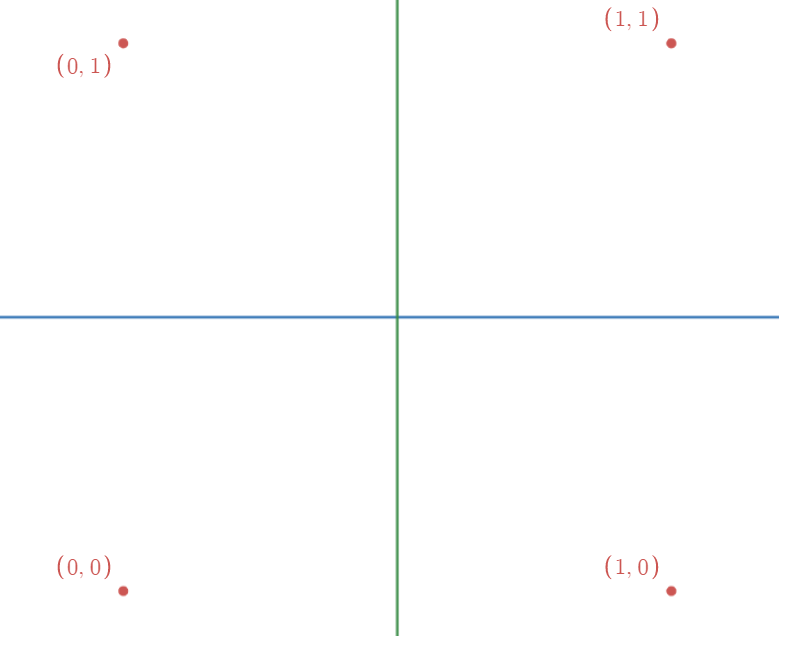
تصویر سناریو اول:
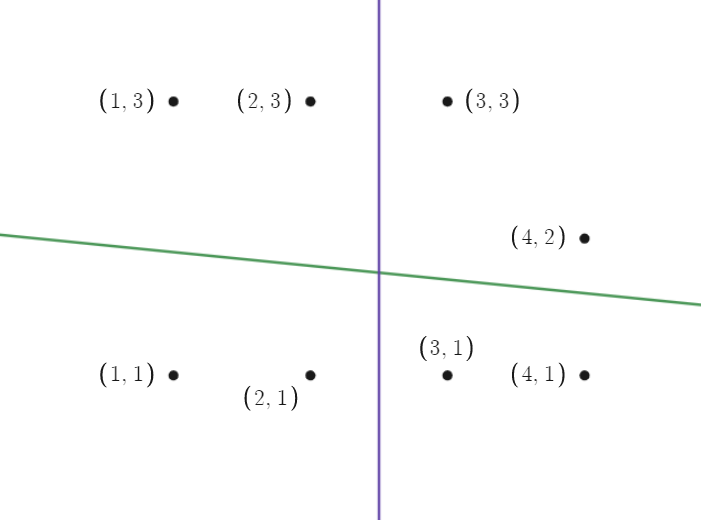
تصویر سناریو دوم: