+ محدودیت زمان: ۲ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
*بین کارهای سنگین اردوی ورودیهای سال بعد دانشگاه، استاد مجتبی برای قدری استراحت به کارتبازی رویآورده اند.*
ابتدا $n$ کارت روی میز قرار دارد که روی هر کارت در ابتدا عدد $a_i$ و پشت آن، عدد $b_i$ قرار دارد. مجتبی کارتبازی را در $k$ مرحله انجام میدهد. در مرحلهی $j$ام، به ازای هر $i$، اگر عدد روی کارت از $t_j$ کمتر مساوی باشد، مجتبی کارت $i$ را برعکس میکند به طوری که عددی که پشت آن بوده اکنون رو قرار میگیرد. پس از طراحی این بازی مجتبی دریافت وقت کافی برای بازی کردن ندارد پس از شما میخواهد جمع اعداد روی کارتها پس از پایان این $k$ مرحله را محاسبه کنید.
# ورودی
در خط اول اعداد $n$ و $k$ آمده اند.
در خط $i$ ام از $n$ خط بعدی دو عدد $a_i$ و $b_i$ آمده اند.
در خط $j$ ام از $k$ خط بعدی عدد $t_j$ آمده است.
$$1 \le n, k \le 200\ 000$$
$$1 \le a_i, b_i, t_j \le 10^9$$
# خروجی
جمع اعداد روی کارتها پس از پایان این $k$ مرحله را چاپ کنید.
# زیرمسئلهها
| زیرمسئله | نمره | محدودیت |
|:-------:|:----------:|:-----------:|
|۱| ۴ | $ n, k \le 1\ 000 $ |
|۲| ۳۱ | $ n, k \le 40\ 000 $ |
|۳| ۶۵ | بدون محدودیت اضافی |
# مثال
## ورودی نمونه
```
5 3
4 6
9 1
8 8
4 2
3 7
8
2
9
```
## خروجی نمونه
```
18
```
اعداد روی کارتها پیش از مرحلهی اول:
$$4, 9, 8, 4, 3$$
اعداد روی کارتها پس از مرحلهی اول:
$$ 6, 9, 8, 2, 7$$
اعداد روی کارتها پس از مرحلهی دوم:
$$6, 9, 8, 4, 7$$
اعداد روی کارتها پس از مرحلهی سوم:
$$4, 1, 8, 2, 3$$
+ محدودیت زمان: ۲ ثانیه
+ محدودیت حافظه: ۵۱۲ مگابایت
----------
*دوستداران استاد مجتبی در انتظار بازگشت او از اردوی جهادی پیراهن میدرند.*
در فیاضکده $n$ روستا با شمارههای ۱ تا $n$ وجود دارد. از هر روستا دقیقا یک جادهی خروجی دارد (دقت کنید که اگر از روستای $A$ بتوان به روستای $B$ رفت، نمیتوان لزوما از روستای $B$ به $A$ نیز رفت، جادهها یکطرفه اند).
استاد در کنار جویباری در روستای شماره 1 نشسته و گذر عمر میبیند. استاد که دلش هوای سفر کرده است میخواهد با شروع از روستای 1، $k$ جاده را بپیماید و در شهری که میرسد مستقر گردد. اهالی هر روستا میخواهند که استاد در روستای آنها مستقر گردد. ریش سفید فیاضکده میتواند یک شهر $p$ را انتخاب کند و جادهی خروجی قبلی آنرا خراب کرده و سپس جاده ای از شهر $p$ به یک شهر $q$ دلخواه بکشد (این شهر $q$ میتواند همان شهر قبلی که $p$ به آن جاده داشت نیز باشد).
حال ریش سفید از شما کمک میخواهد که به ازای هر شهر $i$ به او بگویید چند زوج مرتب $(p,q)$ وجود دارد که استاد در نهایت در شهر $i$ مستقر گردد.
# ورودی
در خط اول دو عدد $n$ و $k$ آمده اند.
در خط $i$ام از $n$ خط بعدی عدد $U_{i}$ آمده که نشان دهنده شماره روستایی است که روستای $i$ ام به آن جاده دارد.
$$ 1 \le n \le 100\ 000 $$
$$ n \le k \le 10^{18} $$
# خروجی
در خط $i$ ام از $n$ خط خروجی جواب را به ازای شهر با شماره $i$ چاپ کنید.
# زیرمسئلهها
| زیرمسئله | نمره | محدودیت |
|:-------:|:----------:|:-----------:|
|۱| ۱۰ | $ n \le 100 $ |
|۲| ۳۷ | $ n \le 3\ 000 $ |
|۳| ۳۳ | $ U_{i} \neq U_{j}\ (1 \le i < j \le n) $ |
|۴| ۲۰ | بدون محدودیت اضافی |
# مثال
## ورودی نمونه ۱
```
5 7
5
1
4
3
2
```
## خروجی نمونه ۱
```
1
2
3
3
16
```
جفت مرتبهای درست به ازای هر $i$ عبارتند از :
$$1 : (1,1) $$
$$2 : (1,2), (2,2)$$
$$3 : (1,3), (2,3), (5,4)$$
$$4 : (1,4), (2,4), (5,3)$$
$$5 : (1,5), (2,1), (2,5), (3,1), (3,2), (3,3), (3,4), (3,5), (4,1), (4,2) (4,3), (4,4), (4,5), (5,1), (5,2), (5,5) $$
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۵۱۲ مگابایت
----------
*استاد مجتبی یک بازی جدید دانلود کرده است.*
بازی شامل یک جدول $(m+2) \times n$ است که در آن توپی از یک خانهای سطر اول به پایین پرت میشود و در نهایت به یک خانه از سطر $(m+2)$ام میرسد.
در هریک از سطرهای ۲ تا $(m+1)$ام یک مانع سوراخ دار قرار دارد. مانع سوراخ دار سطر $i$ام را میتوان با ۳ عدد $A_{i}, B_{i}, C_{i}$ نشان داد ($A_{i} \le C_{i} \le B_{i}$)، به این معنی که این مانع از خانه $(i,A_{i})$ تا خانه $(i,B_{i})$ را پوشش میدهد و در خانه $(i,C_{i})$ از آن یک سوراخ دارد. اگر توپ از بالا به این مانع برخورد کند، قل میخورد و از خانه ی دارای سوراخ خارج میشود و به مسیرش به سمت پایین ادامه میدهد.
برای قرار دادن مانع $i$ام، بازیکن باید $D_{i}$ هزینه بپردازد. هدف بازی این است که بتوان با کمترین هزینه طوری مانعها را قرار داد که توپ از هر یک از خانههای سطر اول شروع کند، به یک خانه یکسان از سطر آخر برسد (مثلا توپ از هرجا شروع کند به خانهی دوم از سطر آخر برسد).
استاد که در بند سوراخ و خانههای خالی جدول نیست، از شما میخواهد که بازی را برای او انجام دهید.
# ورودی
در سطر اول به ترتیب دو عدد $m$ و $n$ آمده اند.
در سطر $i$ام از $m$ سطر بعدی ورودی، ۴ عدد $A_{i+1}$ ،$B_{i+1}$ ،$C_{i+1}$ و $D_{i+1}$ آمده اند.
$$ 1 \le m \le 100\ 000 $$
$$ 1 \le n \le 1\ 000\ 000\ 000$$
$$ 1 \le A_{i+1}\le C_{i+1} \le B_{i+1} \le n$$
$$ 1 \le D_{i+1} \le 1\ 000\ 000\ 000$$
# خروجی
اگر کار خواسته شده در سوال امکان پذیر نیست عدد $-1$، و در غیر این صورت کمترین هزینه را چاپ کنید.
# زیرمسئلهها
| زیرمسئله | نمره | محدودیت |
|:-------:|:----------:|:-----------:|
|۱| ۱۱ | $ m \le 10, n \le 1\ 000 $ |
|۲| ۱۸ | $ m \le 200 $ |
|۳| ۲۲ | $ m \le 1\ 000 $ |
|۴| ۴۹ | بدون محدودیت اضافی |
# مثال
## ورودی نمونه ۱
```
5 6
2 4 3 5
1 2 2 8
3 6 5 2
4 6 4 7
2 4 3 10
```
## خروجی نمونه ۱
```
25
```
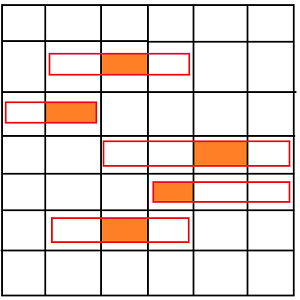
اگر از مانعهای سطر سوم، پنجم و ششم استفاده کنیم، توپ با شروع از هر خانه سطر اول، به خانه سوم از سطر آخر میرسد.