• محدودیت زمان: ۰.۲۵ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

ماریو که با دست خالی حریف کینگ کوپا نمی‌شود، تصمیم به خرید شمشیر ویژه می‌گیرد. ماریو $C_M$ سکه و $G_M$ الماس دارد. از طرفی شمشیر ویژه به $C_S$ سکه و $G_S$ الماس نیاز دارد.

همچنین به شما عدد صحیح $rate$ نشان‌دهنده تعداد سکه در ازای یک الماس داده می‌شود و ماریو می‌تواند با دادن $rate$ سکه یک الماس بگیرد ویا یک الماس بدهد و $rate$ سکه دریافت کند.

ماریو تبدیل را به تعداد دلخواه می‌تواند تکرار کند. آیا می‌تواند شمشیر ویژه را بخرد؟

توجه کنید اگر شمشیر ویژه را بخرد می‌تواند کینگ‌کوپا را شکست دهد و شهر قارچ‌ها و شاهزاده خانم در امان می‌مانند. :)

ورودی🔗

در سطر اول ورودی به ترتیب از چپ به راست دو عدد می‌آید که اولی $C_M$ و دومی $G_M$ خواهد بود. در سطر بعدی هم دو عدد $C_S$ و $G_S$ خواهند آمد. و در سطر سوم هم $rate$ که یک عدد صحیح است خواهد آمد.

$0 \le C_M, G_M, C_S, G_S \le 10$ $1 \le rate \le 10$

خروجی🔗

در تنها سطر خروجی اگر ماریو می‌توانست شمشیر ویژه را بخرد Yes و در غیر اینصورت No را خروجی دهید.

به بزرگی و کوچکی حروف توجه کنید.

مثال🔗

ورودی نمونه ۱🔗

5 2
9 0
3

خروجی نمونه ۱🔗

Yes

اگر ماریو ۲ الماس خود را بدهید ۶ سکه بدست می‌آورد و با ۱۱ سکه‌ای که در مجموع دارد، قادر به خرید شمشیر می‌شود چراکه آن به ۹ سکه نیاز دارد.

ورودی نمونه ۲🔗

10 2
1 4
5

خروجی نمونه ۲🔗

No

هر جور که سکه‌ها و الماس‌ها را بهم تبدیل کند نمی‌تواند شمشیر ویژه را بخرد.

• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

لایتین مکوئین در کاپ پیستون شرکت کرده‌است؛ ولی از آن‌جا رقابت بسیار تنگاتنگ بود یادش نمیاد چه کسی اول شده! مسابقه در تعداد دور مشخص برگزار شده و طول یک دور را می‌دانیم. همچنین سرعت هر ماشین و میزان توقف ماشین‌ها را مکوئین به ما می‌دهد.

به او بگویید چه کسی اول شده قبل از آنکه نتایج رسماً اعلام شود.

توجه کنید که مکوئین خود سرعت است :)

ورودی🔗

در سطر اول ورودی، به ترتیب دو عدد صحیح تعداد دور مسابقه $loop$ و مسافت هر دور به متر $length$ از چپ به راست می‌آیند. $1 \le loop, length \le 200$

سپس در سطر بعد یک عدد $n$ نشانگر تعداد ماشین‌ها می‌آید. $1 \le n \le 100$

در سطر $i$ام از $n$ سطر بعد دو عدد می‌آید که اطلاعات ماشین $i$ را نشان می‌دهد. عدد اول $t_i$ یا میزان زمان تعویض لاستیک و سوخت‌گیری در طول کل مسابقه برحسب ثانیه است و عدد دوم $v_i$ سرعت ماشین برحسب متر بر ثانیه است. $0 \le t_i \le 100$ $1 \le v_i \le 100$

خروجی🔗

در تنها سطر خروجی شماره ماشین برنده را خروجی دهید.

تضمین می‌شود هیچ دو ماشینی همزمان برنده مسابقه نشوند.

مثال🔗

ورودی نمونه ۱🔗

20 10
3
100 100
50 4
1 2

خروجی نمونه ۱🔗

2

ورودی نمونه ۲🔗

200 200
3
100 100
50 90
0 80

خروجی نمونه ۲🔗

2

• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

طهماسب امروز ۴ ساله شد و بعد از آن‌که شمع‌ها رو فوت کرد تا ۱۲۰ ساله بشه تصمیم به برش کیک تولد خود گرفت. طهماسب $n$ برش روی کیک در زاویه‌های مختلف زد تا کیک را بین $n$ نفر حاضر در جشن تقسیم کند. بعد از زدن برش‌ها او بزرگترین تکه را برای خود برداشت.

به مامان طهماسب که نگران سلامتی اوست بگویید که طهماسب چند درصد از کیک را خورده است.

ورودی🔗

در سطر اول عدد صحیح $n$ می‌آید. $2 \le n \le 100 \, 000$ در سطر دوم $n$ عدد با فاصله می‌آیند که $i$امین آن‌ها $degree_i$ درجه برش $i$ام با دقیقاً ۴ رقم دقت اعشار است. $0 \le degree_i < 360$ تضمین می‌شود هیچ دو برشی در یک مکان زده نشود.

خروجی🔗

در تنها خط خروجی درصد کیکی که طهماسب خورده را خروجی دهید. اگر اختلاف جواب شما با جواب سوال حداکثر $0.001$ باشد. پاسخ درست در نظر گرفته می‌شود.

مثال🔗

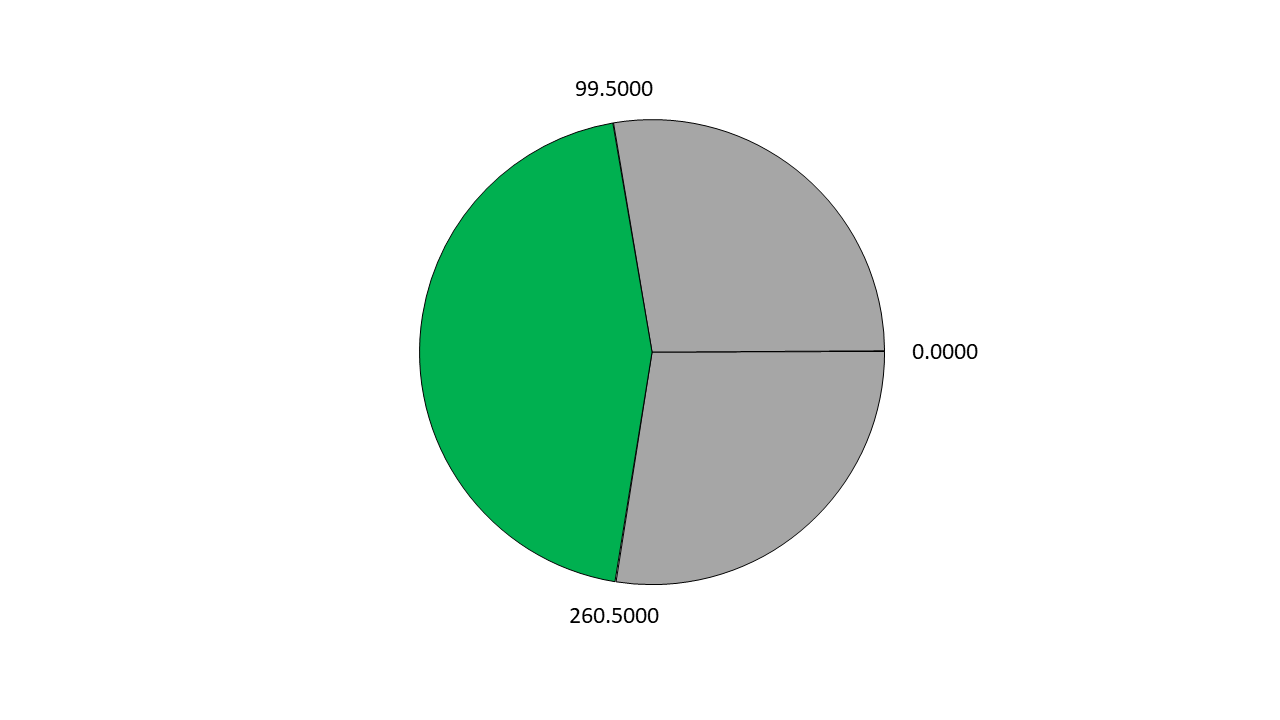
ورودی نمونه ۱🔗

3
0.0000 260.5000 99.5000

خروجی نمونه ۱🔗

44.72222222

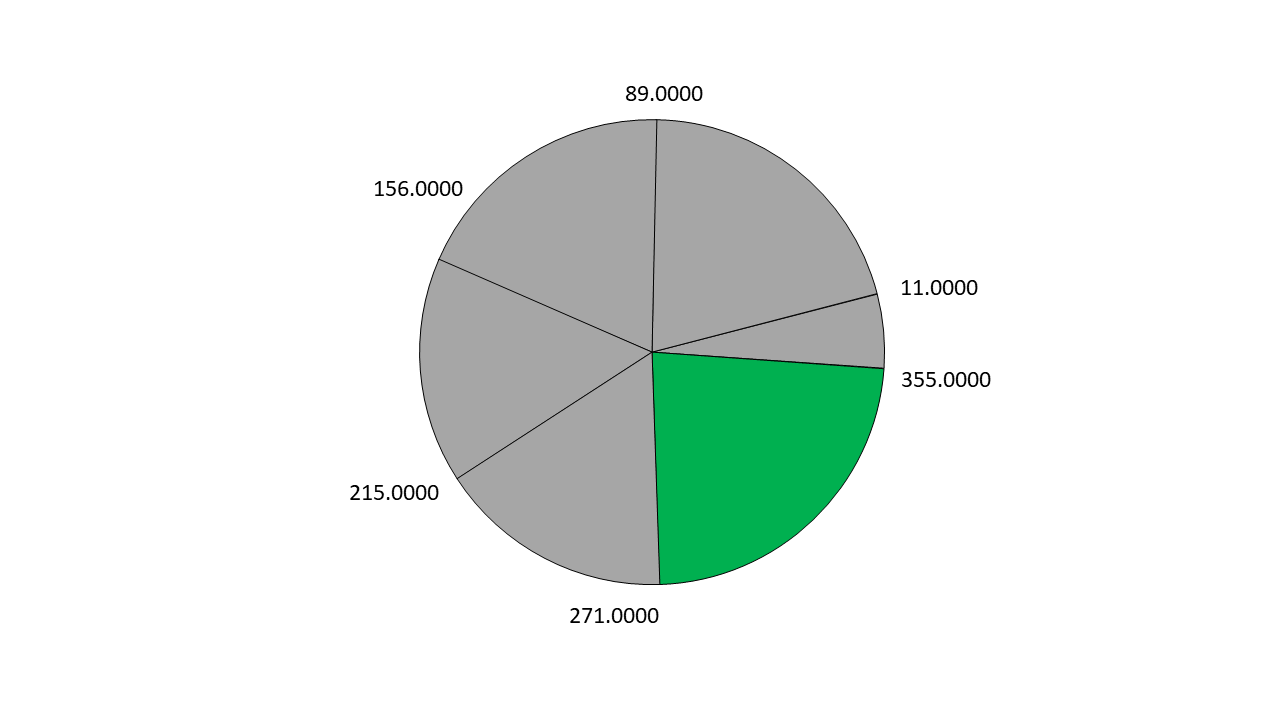
ورودی نمونه ۲🔗

6
11.0000 89.0000 355.0000 271.0000 215.0000 156.0000

خروجی نمونه ۲🔗

23.334

• محدودیت زمان: ۲ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

یک جمله معروف هست که میگه اجسام در دیدگاه میکروسکوپی و ماکروسکوپی یک شکل‌ند. یا به عبارتی اگر یک جسم رو با ذره‌بین خیلی قوی ببینیم یا کلی ازش فاصله بگیریم, یک‌چیز دیده خواهد شد.

$\space$

رها بعد از دیدن این جمله به فکر فرو می‌رود. او به یک کوتریس که نزدیکش بود خیره می‌شود و در می‌یابد که در هر خانه کوتریس که سفید باشد خود کوتریس اولیه و اگر سیاه باشد عکس کوتریس اولیه تکرار شده.

از آنجا که جدول بی‌انتهاست, او از شما سوالاتی درباره با رنگ خانه‌های جدول با دقت‌های مختلف می‌پرسد. توجه کنید در دقت اول خود جدول دیده می‌شود. در دقت دوم هر خانه از کوتریس دقت اول خود به صورت کوتریسی که گفته شد دیده می‌شود و $\dots$

کوتریس یا مخفف کوئرا ماتریس در این سوال جدولی است که هر خانه آن سفید یا سیاه است.

منظور از عکس کوتریس $Q$ یک کوتریس با ابعاد مشابه $Q$ است که رنگ خانه‌های متناظرش بر خلاف $Q$ است.

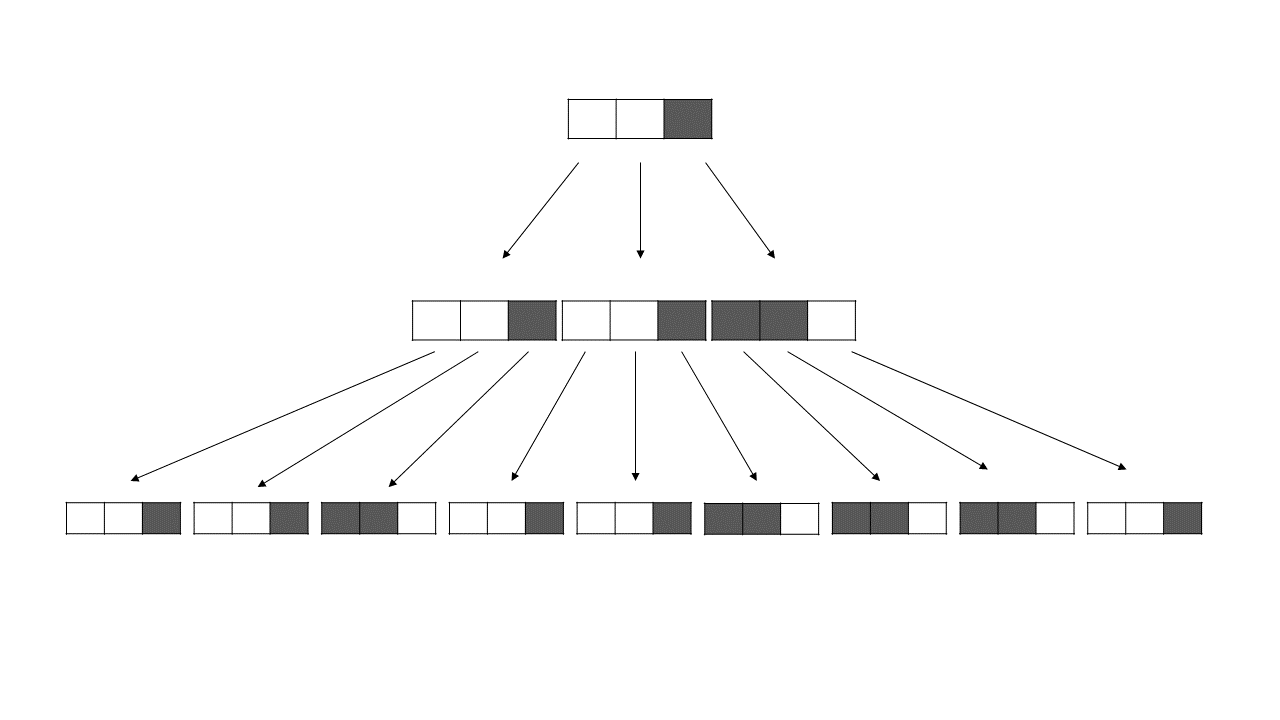
توجه کنید در کوتریس اولیه تعداد خانه‌های سفید بیشتر از خانه‌های سیاه است و به همین دلیل اگر با دقت کم به جدول نگاه کنیم رنگ غالب را خواهیم دید!

ورودی🔗

در سطر اول ورودی دو عدد صحیح $n$ تعداد سطرها و $m$ تعداد ستون‌ها به ترتیب از چپ به راست می‌آید. $1 \le n, m \le 1000$ در $n$ سطر بعد در هر سطر رشته‌ای $m$ حرفی از اعداد ۰ و ۱ بدون فاصله می‌آید که ۰ نشانگر سفید و ۱ نشانگر سیاه است.

در سطر بعدی عدد صحیح $q$ نشانگر تعداد پرسش‌های رها می‌آید. $1 \le q \le 100 \, 000$ در $q$ سطر بعد در هر سطر ۳ عدد صحیح $k_i$ و $x_i$ و $y_i$ می‌آید که در واقع رها از شما می‌پرسد در کوتریس دقت $k_i$ رنگ خانه واقع در سطر $x_i$ از بالا و ستون $y_i$ از چپ چه چیزی است. $1 \le k_i \le 6$ $1 \le x_i \le n^{k_i}$ $1 \le y_i \le m^{k_i}$ اکیداً توصیه می‌شود مراقب محدودیت‌ها باشید!

خروجی🔗

یک سطر با $q$ حرف در خروجی بنویسید که حرف $i$ـم پاسخ پرسش $i$ باشد. به ازای پاسخ سفید ۰ و به ازای پاسخ سیاه ۱ خروجی داده شود.

مثال🔗

ورودی نمونه ۱🔗

1 3
001
6
1 1 1
1 1 2
1 1 3
2 1 2
2 1 6
2 1 9

خروجی نمونه ۱🔗

001010

شکل این کوتریس در سوال آمده است.

ورودی نمونه ۲🔗

2 2
10
00
6
1 1 1
1 1 2
2 3 1
2 3 2
2 3 3
2 4 3

خروجی نمونه ۲🔗

101010

• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

پیتر در لندن می‌خواهد پیامی برای مایکل در جردن ارسال کند. از آن‌جا که مایکل در تهران است، پیتر باید پیام خود را در بستر پیام‌رسانی وطنی ارسال کند. پیام‌رسان وطنی به حرف x حساس است و هر جا که پیتر این حرف را بزند اول پیام‌رسان پیام فعلی پیتر را برعکس می‌کند و سپس این حرف را به انتها آن اضافه می‌کند. برای مثال اگر او abcx بنویسد و ارسال کند مایکل cbax دریافت خواهد کرد.

مایکل که درگیر بسکتبال است، پیام پیتر را به شما نشان می‌دهد و از شما می‌خواهد آنچه واقعاً منظور پیتر بوده را به او بگویید.

ورودی🔗

در تنها سطر ورودی یک رشته ناتهی متشکل از حروف کوچک انگلیسی می‌آید که طول آن حداکثر صدهزار است.

خروجی🔗

در تنها سطر خروجی رشته ای که هدف پیتر بوده را خروجی دهید. توجه کنید که تحت شرایط گفته شده جواب مساله یکتاست.

مثال🔗

ورودی نمونه ۱🔗

cbax

خروجی نمونه ۱🔗

abcx

$a \to ab \to abc \to cbax$

ورودی نمونه ۲🔗

xabcxefx

خروجی نمونه ۲🔗

cbaxefxx

$c \to cb \to cba \to abcx \to abcxe \to abcxef \to fexcbax \to xabcxefx$

• محدودیت زمان: ۲ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

شهر اعداد که پیشتر شورای شهر خود را تشکیل داده بود، به ناکارآمدی شورا حتی اگر همه‌شان کارا باشند پی‌برد. مردم شهر اینک نیاز به پادشاه را درک کرده‌اند و تصمیم به انتخاب پادشاه می‌گیرند.

اما مشکل اینجاست که مردم نظر یکسانی درباره فرد شایسته ندارند. به طور دقیق‌تر هر فردی در شهر اعداد یک عدد دارد و از نظر فردی با عدد $x$ فردی با عدد $y$ بهتر از فردی با عدد $z$ است اگر و تنها اگر $y \oplus x > z \oplus x$ باشد. که در اینجا منظور از علامت $\oplus$ عملیات xor است.

حال اعداد شهروندان شهر به شما داده می‌شود و بگویید در همه حالات انتخاب دو نفر و یک داور، هر شهروند چند بار پیروز می‌شود. توجه کنید داور می‌تواند شرکت کننده هم باشد.

برای درک بهتر می‌توانید به توضیحات نمونه مراجعه کنید.

ورودی🔗

در سطر اول $n$ تعداد شهروندان می‌آید. در سطر بعد $n$ عدد می‌آید که $i$امین آن‌ها $a_i$ عدد شهروند $i$ است. $1 \le n \le 1000 \, 000$ $0 \le a_i \le 10^9$

خروجی🔗

در تنها سطر خروجی تعداد برتری های افراد با فاصله مطلوب است.

مثال🔗

ورودی نمونه ۱🔗

3
0 2 3

خروجی نمونه ۱🔗

4 2 3

ورودی نمونه ۲🔗

5
0 0 1 4 5

خروجی نمونه ۲🔗

6 6 10 11 12

• محدودیت زمان: ۲ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

پارسا نذر کرده‌بود اگر نمره یک درس کذایی رو ۲۰ بگیره $t$ روز به بچه‌ها شکلات میده. حال نمرات درس اومده و او باید به نذرش عمل کنه. او هر روز یک گونی شکلات با خودش به بیرون می‌بره و بچه‌ها صف می‌کشن تا پارسا بهشون شکلات بده. در هر گونی تعدادی بسته شکلات وجود داره که از بالا به پایین چیده شده و درون هر بسته تعدادی شکلات قرار داره. پارسا در هر نوبت تعدادی بسته از بالا گونی برمی‌داره و به اولین نفر صف میده. اگر بچه‌ها هم‌اندازه شکلات نگیرن از دست پارسا دلخور می‌شن. پارسا که نمی‌خواهد هیچ کس دلخور باشه از شما می‌پرسه بچه‌ها اگر چند نفر باشن ممکنه دلخوری به وجود نیاد؟

توجه کنید که همه بسته‌های شکلات بین افراد پخش خواهند شد.

ورودی🔗

در سطر اول ورودی $t$ تعداد روز‌ها می‌آید و سپس اطلاعات $t$ روز به شرح زیر می‌آید.

در سطر اول روز $i$ عدد $n_i$ نشانگر تعداد بسته‌های درون گونی روز $i$ می‌آید و سپس در خط بعد $n_i$ عدد صحیح با فاصله از هم می‌آیند که عدد $j$ام آنها یا $a_{ij}$ تعداد شکلات‌های بسته $j$ام از بالا است.

$1 \le t \le 10 \, 000$ $1 \le n_i, \sum_{i=1}^t n_i \le 1 \, 000 \, 000$ $1 \le a_{ij} \le 10^{12}$

خروجی🔗

برای هر روز به ترتیب پاسخ را در دو سطر خروجی دهید.

در سطر اول هر روز تنوع تعداد افراد ممکن و در سطر دوم همه حالات تعداد افراد ممکن به صورت صعودی.

مثال🔗

ورودی نمونه ۱🔗

3
2
1 2
3
1 2 3
4
4 1 3 4

خروجی نمونه ۱🔗

1
1
2
1 2
2
1 3

در روز دوم ۳ بسته شکلات با تعداد شکلات‌های ۱ و ۲ و ۳ داریم. یک حالت این است که یک نفر در صف باشد و هر ۳ بسته را به او بدهیم و حالت دیگر این است که دو نفر در صف باشند و ۲ بسته اول را به نفر ۱ و بسته آخر را به نفر ۲ بدهیم و بدین شکل هر دو نفر ۳ شکلات گیرشان می‌آید.