+ محدودیت زمان: ۰.۵ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
ویروس جدیدی به جان سیستم رهنما افتاده است. نام این ویروس «کاپی» بوده و با کپی کردن فایلها حافظه را پر میکند! نحوهی کپی کردن «کاپی» هم به این صورت است که ابتدا یک عدد $n$ به صورت تصادفی انتخاب کرده و سپس فایلی را انتخاب کرده و آن را کپی میکند. بعد نام این فایل جدید را به این صورت انتخاب میکند که به تعداد $n$ بار اول اسمش عبارت `copy of` میآورد و سپس نام فایل اولیه را میآورد؛ برای مثال اگر فایلی به نام `you` را بخواهد کپی کند و عدد انتخابی سه باشد، نام فایل کپی شده برابر `copy of copy of copy of you` خواهد شد. (دقت کنید که بعد از هر عبارت `copy of` یک فاصله میآید.)
متاسفانه حملات پی در پی آنتیویروسهای رهنما «کاپی» را ضعیف کرده است. با دادن نام فایل و تعداد بار کپی کردن فایل، نام فایل کپی شده را خروجی دهید.
# ورودی
در تنها سطر ورودی عدد $n$ و رشتهی $s$ آمده است که به ترتیب نمایانگر عدد تصادفی انتخاب شده توسط ربات و نام فایل انتخاب شده، میباشد. طول رشته $s$ حداکثر صد میباشد. تضمین میشود که نام فایل انتخاب شده فقط از حروف کوچک انگلیسی درست شده است.
$$ 0 \le n \le 100 $$
# خروجی
در تنها سطر خروجی نام فایل کپی شده را چاپ نمایید.
# مثال
## ورودی نمونه ۱
```
3 copyof
```
## خروجی نمونه ۱
```
copy of copy of copy of copyof
```
## ورودی نمونه ۲
```
1 shoma
```
## خروجی نمونه ۲
```
copy of shoma
```
کمک به کاپی
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
در شهر مرد مالیاتچی مردم به زبان Taxlang با یک دیگر سخن میگویند که شامل حروف T و A و X و M و N میباشد. بدلیل اینکه این شهر مربوط به سال 1717 قبل از میلاد است برای نوشتن یک عبارت، بلوک هایی متناظر با کاراکتر های آنرا بر روی دیواره ی غارها حک میکنند. به طور دقیق تر این زبان از چپ به راست خوانده شده و شامل بلوک هایی به طول ۵ و ارتفاع ۳ میباشد و هر بلوک دقیقا با یکی از حروف این زبان متناظر است که با مشاهده ورودیهای نمونه میتوانید به راحتی تناظر میان آنها را کشف کنید.
مرد مالیاتچی که متاسفانه هنوز وقت نکرده است که خواندن یاد بگیرد، متنی به زبان خودشان به شما داده و ترجمهی آن را از شما میخواهد.
# ورودی
ورودی شامل سه خط از کاراکترها میباشد. طول هر خط مضربی از ۵ بوده و حداکثر ۱۰۰ میباشد.
تضمین میشود که ورودی معتبر بوده و دقیقا یک ترجمه مناسب برای آن وجود دارد.
# خروجی
در تنها سطر خروجی ترجمه متن داده شده را خروجی دهید.
# مثال
## ورودی نمونه ۱
```
*****
oo*oo
oo*oo
```
## خروجی نمونه ۱
```
T
```
## ورودی نمونه ۲
```
oo*oo
o***o
*ooo*
```
## خروجی نمونه ۲
```
A
```
## ورودی نمونه ۳
```
*ooo*
oo*oo
*ooo*
```
## خروجی نمونه ۳
```
X
```
## ورودی نمونه ۴
```
**o**
*o*o*
*ooo*
```
## خروجی نمونه ۴
```
M
```
## ورودی نمونه ۵
```
*ooo*
*o*o*
*ooo*
```
## خروجی نمونه ۵
```
N
```
## ورودی نمونه ۶
```
*****oo*oo*ooo***o**oo*oo*ooo*
oo*ooo***ooo*oo*o*o*o***o*o*o*
oo*oo*ooo**ooo**ooo**ooo**ooo*
```
## خروجی نمونه ۶
```
TAXMAN
```
تکسلنگ
+ محدودیت زمان: ۰.۵ ثانیه
+ محدودیت حافظه: ۱۲۸ مگابایت
*****
برای کنترل جهان باید از کنترل کولر شروع کرد!
«رادزینکا دوبرامیل ویچشسلافوویچ»
به تازگی مطّلع شدیم که علاوه بر آقای خطری، آقای بیخطر هم میخواهد برای شرکت در «انتخابات ریاست کولر» نامزد شود. آقای خطری پس از اطّلاع از این خبر، بسیار نگران میشود و تصمیم میگیرد با آقای بیخطر مذاکره کند و او را از این امر منصرف کند.
امّا آقای بیخطر که از آقای خطری بسیار میترسد، شروع به فرار میکند تا این که در ترامپولین شماره $n$ از مسیر ترامپولینی گیر میافتد.
مسیر ترامپولینی متشکل از $n$ ترامپولین است که در یک صف دور کرهی زمین قرار دارند و **به ترتیب ساعتگرد** از $1$ تا $n$ شمارهگذاری شده اند. اگر کسی روی ترامپولین شماره $i$ بپرد، $i$ ترامپولین (بطور ساعتگرد) جلوتر خواهد رفت. این روند تا زمانی که دو نفر در یک خانه قرار نگیرند ادامه خواهد داشت!
مثلن اگر $n=3$ و کسی روی ترامپولین اوّل بپرد، ابتدا یک واحد جلو میرود و به ترامپولین دوم میرسد. سپس دو واحد جلو خواهد رفت و به ترامپولین اوّل بازخواهد گشت. این روند مدام تکرار میشود.
آقای خطری که به دنبال آقای بیخطر است، به مسیر ترامپولینی میرسد امّا از شمارهی ترامپولینها آگاه نیست. حال او از شما میخواهد به او بگویید به ازای چند انتخاب ترامپولین اوّلیّه، او سرانجام آقای بیخطر را خواهد یافت.
# ورودی
در ورودی تنها یک عدد طبیعی $n$ داده شده است.
$$ 1 \le n \le 10^9 $$
# خروجی
در تنها خط خروجی باید یک عدد صحیح چاپ کنید که برابر تعداد ترامپلینهایی است که آقای خطری با شروع از آنها سرانجام به ترامپلین آقای بیخطر میرسد.
# مثال
## ورودی نمونه ۱
```
1
```
## خروجی نمونه ۱
```
1
```
در این نمونه، آقای خطری با شروع از ترامپلین شماره ۱ همیشه در آن میماند.
## ورودی نمونه ۲
```
6
```
## خروجی نمونه ۲
```
2
```
در این نمونه، آقای خطری میتواند از ترامپلین شماره ۳ و یا ۶ شروع کند. در صورت شروع از ترامپلین شماره ۳، پس از یک حرکت به ترامپلین شماره ۶ میرسد.
ترامپُلین
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
علی آقا رانندهی اسنپ در شکرستان است. شکرستان، $n$ تا تقاطع دارد که با $m$ جادهی یکطرفه به هم وصل شدهاند.
علی آقا از شهری خوشش میآید که اگر از هر تقاطعی شروع به حرکت کند، نتواند با طی کردن تعدادی جاده برگردد به همان تقاطعی که شروع کرده بود.
میدانیم که علی آقا از شکرستان خوشش میآید.
علی آقا مشتری زیادی ندارد؛ برای همین میخواهد که از چند تا جاده خلاف جهت معین شده عبور کند تا مشتری بیشتری نصیبش شود.
در ضمن علی آقا میخواهد **حداقل از یک جاده خلاف جهتش عبور کند.**
از جایی که علی آقا خیلی هم خلاف نیست میخواهد کمترین تعداد جاده را خلاف برود.
علی آقا تصمیم گرفت که یک سری جاده را برای خلافرفتن انتخاب کند بطوری که **از شهری که با عوض کردن جهت جادههای انتخاب شده ایجاد می شود خوشش بیاید.**
به علی آقا کمک کنید که بداند حداقل جهت چند جاده را باید عوض کند و آنها چه جادههایی هستند.
# ورودی
در خط اول دو عدد $n$ و $m$ آمده است و در $m$ خط بعدی مشخصات جادههای شکرستان آمده است؛ به گونهای که در خط $i+1$ ام ورودی دو عدد $u_i$ و $v_i$ آمدهاست که نشان میدهد جادهی $i$ام از $u_i$ به $v_i$ است.
تضمین میشود بین هیچ دو تقاطعای بیشتر از یک جاده نیست و علی آقا از شکرستان خوشش میآید.
$$1 \le n, m \le 1\ 000\ 000$$
$$ 1 \le v_i \neq u_i \le n $$
# خروجی
در خط اول $t$ کمترین تعداد جاده های لازم که علی آقا باید انتخاب کند را چاپ کنید.
در خط $t$ خط بعدی شماره جادههایی که علی آقا باید انتخاب کند را به هر ترتیبی چاپ کنید.
در صورت وجود چند جواب یکی را به دلخواه چاپ کنید.
# مثال
## ورودی نمونه ۱
```
2 1
1 2
```
## خروجی نمونه ۱
```
1
1
```
## ورودی نمونه ۲
```
5 7
3 4
2 4
2 3
1 4
1 3
5 3
5 4
```
## خروجی نمونه ۲
```
1
5
```
علی خلافه
+ محدودیت زمان: ۲ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
نقطهبازی یک بازی قدیمی است. این بازی معمولا بین دو بازیکن در یک صفحه $N \times M$ که شامل $N$ ردیف است که در هر ردیف $M$ نقطه است، انجام میشود. ردیفها را از بالا به پایین با ۱ تا $n$ و ستونها را از چپ به راست با ۱ تا $m$ نامگذاری میکنیم.
بازی به این صورت است که هر کس در نوبت خود بین دو نقطهی مجاور که قبلا بین آنها پارهخطی کشیده نشده است ، پارهخطی میکشد.
هر گاه حرکت کسی منجر به ساخت تعدادی مربع $1 \times 1$ شود، به تعداد مربعها امتیاز میگیرد و **همچنین حرکت بعدی را نیز باید خودش انجام دهد**.
بازی وقتی تمام میشود که نشود پارهخطی کشید.
همانطور که میدانید یک برنامهنویس بیشتر از هر چیز به تفریح و سرگرمی نیاز دارد. به همین منظور ناصر و یاسر که دو تا از خوبهای شرکت رهنما هستند، تصمیم میگیرند با هم نقطهبازی کنند.
از آنجایی که ناصر اعتقاد دارد که معمولا شروع کننده بازی، برنده بازی است **همواره** حرکت اول را او انجام میدهد.
بعد از پایان بازی یک مسئله ذهن ناصر را مشغول میکند؛ آیا کسی میتواند بدون دیدن برگه بازی و صرفا با دانستن پارهخطهای کشیده شده نتیجه بازی را بفهمد.
ما از شما میخواهیم به ناصر کمک کنید و برنامهای بنویسید تا صرفا با گرفتن حرکات، نتیجه نهایی را برای ما محاسبه کند.
** (برای فهم بیشتر، شکلی که برای ورودی نمونه دوم کشیده شده را نگاه کنید.) **
# ورودی
در خط اول $n$ و $m$ که ابعاد صفحه هستند داده میشود.
در $ 2\times n \times m - n - m $ خط بعدی در هر خط چهار عدد مانند $(x_{1} , y_{1} , x_{2} , y_{2})$
به شما داده میشود که به معنای این است که نقطهی سطر $x_{1}$ و ستون $y_{1}$ به نقطه سطر $x_{2}$ و ستون $y_{2}$ با یک پارهخط متصل شد.
همچنین تضمین میشود که ناصر و یاسر تنها حرکات مجاز انجام میدهند.(یعنی همواره پارهخط بین دو نقطهی مجاور است که تا به حال بین آنها خطی کشیده نشده است.)
همچنین داریم:
$$ 2 \le n , m \le 200 $$
$$ 1 \le x_{1} , x_{2} \le n$$
$$ 1 \le y_{1} , y_{2} \le m$$
# خروجی
در یک خط دو عدد (که با فاصله از هم جدا شدهاند) چاپ کنید که عدد اول امتیاز ناصر و عدد دوم امتیاز یاسر باشد.
## ورودی نمونه ۱
```
2 2
1 1 1 2
1 2 2 2
2 2 2 1
2 1 1 1
```
## خروجی نمونه ۱
```
0 1
```
## ورودی نمونه ۲
```
2 3
1 1 2 1
1 2 2 2
1 2 1 3
1 1 1 2
2 1 2 2
2 2 2 3
1 3 2 3
```
## خروجی نمونه ۲
```
1 1
```
شکل زیر نمایانگر بازی ورودی نمونه دوم است:
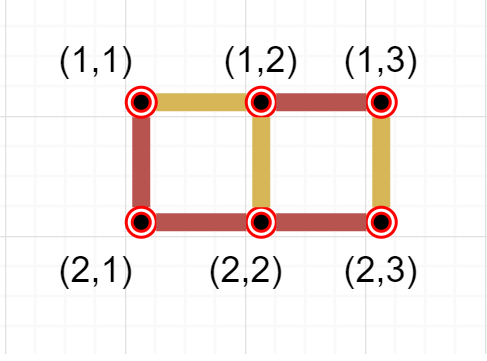
نقطه بازان رهنما
+ محدودیت ز مان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
محمدرضاص که کنکورش را داده، میخواهد در همهی مسابقات برنامهنویسی کوئرا شرکت کند؛ اما درگیریهایش باعث شدند او پس از شروع مسابقه برسد.
محمدرضاص پس از اینکه متوجه شد دیگر نمیتواند در مسابقهی ششم کوئرا شرکت کند، از ناراحتی از هوش رفت. او در خواب و خیال خودرا در یک صفحه شطرنجی با $H$ سطر و $W$ ستون یافت. او دید که سطرهای این جدول با اعداد طبیعی ۱ تا $H$ از بالا به پایین و ستونهای آن با اعداد طبیعی ۱ تا $W$ از چپ به راست شماره گذاری شدهاند و خودش روی خانهی در سطر و ستون اول(خانهی بالا-چپ جدول)، سوار بر یک اسب سفید متنظر حرکت است. همچنین دید که $n$ خانه از صفحه شطرنج شامل مانع هستند (یعنی اسب او نمیتاند وارد آن خانهها شود) و روی خانهی در سطر $H$ و ستون $W$ (خانهی پایین-چپ جدول) دارد مسابقهی کوئرا برگزار میشود!
اسبی که محمدرضاص روی آن سوار است مانند همهی اسبهای شطرنج، میتواند بصورت $L$ حرکت کند. یعنی به خانههایی میتواند برود که فاصله اقلیدسی آنها با خانهی کنونی برابر $\sqrt 5$ است. محمدرضاص با خوشحالی قصد حرکت کردن به سمت خانهی مسابقه کرد، اما متوجه شد که اسب رویاهای او شل است و تنها میتواند به سمت پایین-راست حرکت کند؛ یعنی پس از هر حرکت باید شماره سطر و ستونش زیاد بشود.
دقت کنید که ممکن است محمدرضاص با این وضعیت نتواند به خانهی مسابقه برسد، مثلاً اگر $H = 3$ و $W = 10$ اینگونه میشود.
حال محمدرضاص میخواهد از فضای خیالی خود سوء استفاده کرده و از خود بیشترین تعداد کپی ممکن را بگیرد و از مسیرهای مختلف به محل برگزاری مسابقه برود. (بدون علم به اینکه مسابقه حضوری نیست!)
اکنون محمدرضاص بیدار و هشیار شده و اطلاعات صفحه شطرنج خیالش را به ما داده است. با ورودی گرفتن $W, H$ و خانههای شامل مانع، تعداد مسیرهای مختلفی که محمدرضاص میتوانست با اسب خود از گوشهی بالا-چپ به گوشهی پایین-راست جدول برود را خروجی دهید.
چون که این عدد میتواند بسیار بزرگ باشد، باقیماندهی این عدد پس از تقسیم بر $10007$ را خروجی دهید.
# ورودی
سطر اول ورودی شامل سه عدد $H$ و $W$ و $n$ است که به ترتیب نمایانگر تعداد سطرها و تعداد ستونهای صفحه شطرنج خیالی محمدرضاص و تعداد خانههای شامل مانع آن هستند.
سپس در $i$ مین سطر از هریک از $n$ سطر بعدی، دو عدد $h_i$ و $w_i$ آمدهاند که نمایانگر سطر و ستون $i$مین مانع هستند.
$$0 \le n \le 10$$$$1 \le h_i \le H \le 100\ 000\ 000$$$$1 \le w_i \le W \le 100\ 000\ 000$$
# خروجی
تنها سطر خروجی باید شامل یک عدد باشد که برابر باقیماندهی تعداد مسیرهای محمدرضاص پس از تقسیم بر $10007$ است.
# مثال
## ورودی نمونه ۱
```
1 1 0
```
## خروجی نمونه ۱
```
1
```
## ورودی نمونه ۲
```
7 10 2
1 2
7 1
```
## خروجی نمونه ۲
```
5
```
خیال شطرنجی
+ محدودیت ز مان: ۳ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
بدخواه، بدِ جامعهی هنری را هم میخواهد. او تدارک ساخت فیلمی را داده و از $n$ بازیگر مطرح سینما دعوت کرده که در فیلم او بازی کنند. آنها با دیدن فیلمنامه قبول کردند، غافل از نقشههایی که بدخواه برایشان دارد...
بدخواه در همان روز اول کار، به سراغ فیلمبرداری صحنهی پایانی میرود - صحنهی دوئل. در این صحنه، این $n$ بازیگر حضور دارند و هریک کسی را در ذهن خود هدف میگیرد، بطوری که هرکس توسط دقیقاً یک نفر هدفگرفته شود. بازیگر $i$ـم، بازیگر $p_i$ـم را هدف قرار میدهد. در یک لحظه همهی بازیگرها اقدام به شلیک میکنند اما سرعت عکسالعمل آنها برابر نیست و بازیگر $i$ـم، $t_i$ میلی ثانیه طول میکشد تا ماشه را بچکاند و طعم مرگ را به بازیگر $p_i$ـم بچشاند. بدلیل حرفهای بودن این بازیگرها، هریک دقیقاً به اندازهی مقدار تعیین شده ($t_i$ میلی ثانیه) صبر کرده و سپس بسرعت، هفتتیر را بالا آورده و به هدفش ($p_i$ـمین بازیگر) شلیک میکند. این اعمال در زمان اندک انجام میشود.(میتوان فرض کرد اگر شلیک انجام شود، فرد $p_i$ در لحظهی $t_i$ میمیرد.)
اما بدخواهِ نابکار، در هفتتیر این افتخارات ملی، تیرهای واقعی گمارده و با هر شلیک، یک جوان هنرمند میمیرد. اگر بازیگر $i$ـم قبل از زمان $t_i$ مرده باشد، در لحظهی $t_i$ شلیکی از طرف این بازیگر صورت نمیگیرد.
حال بدخواه سناریو را به شما میدهد (مقدار $t_i$ها و $p_i$ها) و از شما میپرسد که با اجرای این سناریو، در نهایت چند بازیگر زنده میمانند. سپس به امید کشتههای بیشتر، $q$ بار این سناریو را عوض میکند؛ هربار یکی از $t_i$ها را تغییر میدهد و پس از هر تغییر نیز از شما میپرسد که حال چطور؟! و شما باید تعداد بازیگرهای زنده پس از اجرای این سناریو را به او بگویید.
دقت کنید که تغییرات انجام شده باقی میمانند؛ بعنوان مثال دومین تغییر روی سناریو ای صورت میگیرد که پیش از آن، اولین تغییر روی آن اعمال شده است.
# ورودی
سطر اول ورودی شامل یک عدد $n$ است که نمایانگر تعداد بازیگرها در سناریوی بدخواه است.
در سطر دوم ورودی، $n$ عدد متفاوت آمده است. $i$ـمین عدد $p_i$ است که نمایانگر هدف بازیگر $i$ـم در سناریوی اولیه است.
در سطر سوم ورودی، $n$ عدد آمده است. $i$ـمین عدد $t_i$ است که نمایانگر زمان عکسالعمل بازیگر $i$ـم در سناریوی اولیه است.
در سطر چهارم ورودی، یک عدد $q$ آمده است که نمایانگر تعداد تغییرهای سناریو است. سپس در $i$ـمین سطر از $q$ سطر بعدی، دو عدد $b_i$ و $y_i$ آمده است که یعنی در تغییر $i$ـم، زمان عکسالعمل بازیگر $b_i$ـم در سناریو به $y_i$ تغییر میکند.
تضمین میشود که همهی اعداد $t_1, t_2, t_3, ..., t_n, y_1, y_2, y_3, ..., y_q$ متفاوت هستند.
$$ p_i \neq i $$$$2 \le n \le 200\ 000$$
$$0 \le q \le 200\ 000$$
$$1 \le p_i, b_i \le n$$
$$1 \le y_i, t_i \le 1\ 000\ 000\ 000$$
# خروجی
خروجی باید شامل $q + 1$ سطر باشد که هرکدام شامل یک عدد هستند. عدد در سطر اول باید برابر تعداد بازیگرهای زنده درصورت اجرای سناریوی اولیه است. عدد در $i + 1$ـمین سطر باید برابر تعداد بازیگرهای زنده باشد، در صورتی که $i$ تغییر اول روی سناریوی اولیه انجام شود و سناریو را اجرا کنند.
# مثال
## ورودی نمونه
```
4
2 3 4 1
1 3 4 5
3
1 8
2 7
3 6
```
## خروجی نمونه
```
2
2
1
1
```