+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
Shayan, a computer engineering student at the University of Tehran with a great passion for mathematics, is a little bit lazy and always makes the minimum effort to solve every task he comes up with. In the first few weeks of school, Shayan’s little cousin Hadi has a few problems with his math exercises and asks Shayan to help him. These math exercises are all about the sum of digits of a number.
Shayan obviously teaches his little cousin how to solve them, but he also assigns Hadi some exercises to make sure that he really understands the concept. Due to his laziness, Shayan doesn’t want to think of some numbers to use. To save time, he will use a recursive strategy to create $n$ exercises of increasing difficulty that Hadi will use to practice.
The $n$ exercises are defined by Shayan as follows: First, we define an initial exercise made out of a single digit $s_1 = d$. Then, we define the remaining exercises with the following formula:
$$s_n = s_{n-1} * n * s_{n-1}$$
Where $*$ is the operation of concatenation, for example $12 * 34 * 56 = 123456$.
Now that the exercises are ready, help Shayan verify Hadi’s solutions by writing an algorithm that, given the initial digit $d$ and the index $n$ of the exercise, calculates the correct answer, i.e. the sum of the digits of $s_n$.
# input
The first line contains two integers: $d$ and $n$, respectively, the initial digit defined by Shayan and the index of the element of the sequence for which Shayan wants to calculate the sum of the digits.
$$0 \leq d \leq 9$$
$$1 \leq n \leq 60$$
# output
You need to write a single line containing the sum of digits of $s_n$.
It is guaranteed that the result will fit in a normal signed 64-bit integer variable. It will
definitely overflow a 32-bit variable.
# example
### sample input 1
```
1 3
```
### sample output 1
```
11
```
### sample input 2
```
3 11
```
### sample output 2
```
6104
```
A- Shayan's number
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
We have a city with $n$ apartments labeled with postal codes $1$ to $n$. The
$i-$th road in this city, connects apartments $a_i$ and $b_i$. Consider delivering food orders to each apartment in the city in the following manner:
For each $k = 1, 2, ..., n$, Snapp Food wants to solve the following problem:
+ First, deliver order $1$ to apartment $k$.
+ Then, for each of the food orders $2, …, n$ in this sequence, deliver the order to the apartment chosen as follows:
Choose an apartment that still does not have an order delivered to it and is adjacent to an apartment with an order already delivered to it. If there are multiple such apartments, choose one of them at random.
Find the number of ways in which we can deliver orders to the apartments, modulo $10^9 + 7$
# input
The first line of the input is the number of apartments $n$. The following $n$ lines, each define a road from apartment $a_i$ to $b_i$.
$$2 \leq n \leq 200 000$$
$$1 \leq a_i, b_i\leq n$$
# output
For each $k = 1, 2, ... , n$ in this sequence, print a line containing the answer to the problem.
# example
### sample input 1
```
3
1 2
1 3
```
### sample output 1
```
2
1
1
```
### sample input 2
```
5
1 2
2 3
3 4
3 5
```
### sample output 2
```
2
8
12
3
3
```
B- Food Ordering
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
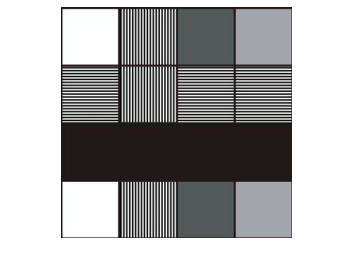
Erfan wants to draw a painting on an $n \times m$ board. He can draw some strips on the board using a paintbrush of width $1$. In each step, he must choose a new color and paint a full column or a full row. He wants to draw an image on the board, but he doesn’t know which color to use first. You must help him find out the order of the colors.
# input
There are multiple test cases in the input. The first line of each test case contains two integers $n$ and $m$ which indicate the count of rows and columns of the board, respectively
Following the first line, there are $n$ lines with $m$ integers $c_{i, j}$($1 \leq i \leq n, 1 \leq j \leq m$) denoting the color in each cell.
$$1 \leq n, m \leq 100$$
$$1 \leq c_{i, j} \leq 1000$$
# output
For each test case, write a single line containing the order of colors used to paint the board. If there are several answers, output the one which is lexicographically smallest (considering each number as a symbol).
# example
### sample input 1
```
4 4
1 5 4 3
6 5 6 6
2 2 2 2
1 5 4 3
```
### sample output 1
```
1 3 4 6 5 2
```
### sample input 2
```
3 2
1 1
2 3
2 3
```
### sample output 2
```
2 3 1
```
C- Painting
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
Misagh, the young adventurer, has found the map to the treasure of Kish Island. The ghost zombie pirate Tabas, the infamous evil pirate of the Persian Gulf has hidden the treasure somewhere inside the Kish Dolphins Park (KDP). KDP is made up of a number of corridors forming a maze. To protect the treasure, Tabas has placed a number of stone blocks inside the corridors to block the way to the treasure. The map shows the hardness of each stone block, which determines how long it takes to destroy the block. KDP has a number of gates on the boundary from which Misagh can enter the corridors. Fortunately, there may be a pack of dynamites at some gates, so if Misagh enters from such a gate, he may take the pack with him. Each pack has a number of dynamites that can be used to
destroy the stone blocks in a much shorter time. Once entered, Misagh cannot exit KDP and enter again, nor can he walk in the area of other gates (so, he cannot pick more than one pack of dynamites).
The hardness of the stone blocks is an integer between 1 and 9, showing the number of days required to destroy the block. We neglect the time required to travel inside the corridors. Using dynamite, Misagh can destroy a block almost immediately, so we can ignore the time required for it as well. The problem is to find the minimum time at which Misagh can reach the treasure. He may choose any gate he wants to enter KDP.
# input
The input consists of multiple test cases. Each test case contains the map of KDP viewed from above. The map is a rectangular matrix of characters. Misagh can move in four directions: up, down, left, and right, but cannot move diagonally. He cannot enter a location shown by asterisk characters (*), even using all his dynamites! The character ($) shows the location of the treasure. A digit character (between 1 and 9) shows a stone block of hardness equal to the value of the digit. A hash sign (#) which can appear only on the boundary of the map, indicates a gate without a dynamite pack. An uppercase letter on the boundary shows a gate with a pack of dynamite. The letter (A) shows that there is one dynamite in the pack, (B) shows that there are two dynamites in the pack, and
so on. All other characters on the boundary of the map are asterisks. Corridors are indicated by dots (.). There is a blank line after each test case. The last line of the input contains two dash characters (--).
The width and the height of the map are at least 3 and at most 100 characters
# output
For each test case, write a single line containing a number showing the minimum number of days it takes Misagh to reach the treasure, if possible. If the treasure is unreachable, write IMPOSSIBLE.
# example
### sample input 1
```
*****#*********
*.1....4..$...*
*..***..2.....*
*..2..*****..2*
*..3..******37A
*****9..56....*
*.....******..*
***CA**********
*****
*$3**
*.2**
***#*
--
```
### sample output 1
```
1
IMPOSSIBLE
```
D- Kish Island
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
Snapp Food wants to praise the best restaurants according to their in-app scores. Each restaurant has introduced and sent its representative to Snapp Food’s center.
There are $n$ representatives who are given ID numbers $1$ through $n$, standing in a row from left to right. Initially, the ID number of the $i$-th person from the left is $p_i$.
Snapp Food wants you to rearrange the representatives in ascending order of the ID number from left to right, by repeatedly doing the three kinds of operations below. You can do these operations any number of times (possibly zero) in any order:
+ Choose an integer $i(1 \leq i \leq n$), pay the cost $a_i$, and move representative $i$(the person with the ID number $i$) to any position of your choice.
+ Choose an integer $i(1 \leq i \leq n$), pay the cost $b_i$, and move representative $i$ to the left end of the row.
+ Choose an integer $i(1 \leq i \leq n$), pay the cost $b_i$, and move representative $i$ to the right end of the row.
Minimize the total cost you pay before achieving the objective.
# input
The first line of the test case is the number of representatives $n$.
In the next line of the input, the representative IDs ($p_i$) are separated by space.
The following $n$ lines, each includes the three aforementioned costs: $a_i, b_i, c_i$.
$$1 \leq n \leq 2 \times 10^5$$
$$1 \leq p_i \leq n$$
$$1 \leq a_i, b_i, c_i \leq 10^9$$
$$p_i \neq p_j (i \neq j)$$
all values in input are integers.
# output
Print the minimum total cost you need to pay before achieving the objective.
# example
### sample input 1
```
3
3 1 2
9 3 5
8 6 4
9 4 6
```
### sample output 1
```
6
```
E- Restaurant Scores
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
Fast-forward to 2031, when (fingers-crossed!) UTCPC has long been a competition that happens in a real physical location, and not just a boring online contest anymore. Shayan and Soroush are thinking about the logistics of organizing next year’s UTCPC 2032: among many other things, they have to rent a building big enough to accommodate everyone!
In order to rent a space of the right size, they want to know the maximum number of people who will be present at the same time on that day. Since they cannot predict the future, they decide to look at data from last year’s event. Unfortunately, no one recorded this exact information, but luckily, at the entrance, there was a turnstile that continuously logged the entry and exit of the people (without authenticating them).
Because of a timezone bug on the turnstiles, the events log is in a weird random order. However, the raw timestamp of each event was preserved correctly. Help organize a successful UTCPC 2032 by calculating, starting from this raw data, the maximum number of people that were in the building at any given time during the last UTCPC!
# input
The first line contains the integer $n$, the total number of events registered by the turnstiles.
The next $n$ lines contain two integers $x_i$ and $y_i$ respectively: the type of event('1' if a person enters, and '-1' if a person exits) and the exact second at which the event was registered.
$$1 \leq n \leq 10^5$$
$$0 \leq y_i \leq 10^6$$
+ $n$ is always even: no one can leave before entering, and all attendees will leave before the end of the event.
+ If a person leaves the building at the exact same second when another person is entering, they
are not counted as being at the event at the same time.
# output
You need to write a single line containing the maximum number of people who were present at the event at the same time that day
# example
### sample input 1
```
4
1 3
1 2
-1 4
-1 5
```
### sample output 1
```
2
```
### sample input 2
```
4
1 0
1 1
-1 1
-1 2
```
### sample output 2
```
1
```
F- UTCPC
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
Hadi loves organizing computer science competitions such as UTCPC. Because of this, he often needs to have online meetings with sponsors, professors, volunteers, and so on.
To keep track of all these meetings, he naturally uses a calendar, but the meetings can get so frequent that sometimes more than one meeting is scheduled to take place at the same time! Hadi is keeping up with this for now (virtual meetings, multiple browser windows, nodding and smiling to the camera, …) but he agrees it should really be avoided as much as possible.
We consider two meetings to happen at the same time even if they just touch, for example a meeting taking place from time 1 to time 3 overlaps with another taking place from time 3 to time 6, because William needs some time to switch meetings, he cannot finish one meeting and immediately be connected to the other meeting.
Hadi asked his friend Shayan to implement an algorithm to reduce meeting overlap in his calendar. The calendar has $n$ meetings, the $i$-th of which starts at time $L_i$ and ends at time $R_i$. We define the “schedule cost” as the maximum number of meetings that Hadi is attending simultaneously. Shayan’s algorithm is allowed to cancel $k$ meetings and wants to minimize the cost of the new schedule.
Help Shayan write the algorithm for Hadi’s calendar!
# input
The first line contains two integers: $n$ and $k$ respectively, the total number of meetings and the maximum number of meetings that Shayan’s algorithm can cancel.
Each of the next $n$ lines contain a pair of integers: $L_i$ and $R_i$, respectively, the starting and the ending time of the $i$-th meeting.
$$2 \leq n \leq 10^5$$
$$2 \leq L_i \lt R_i \leq 10^5$$$$1 \leq k \lt n$$
+ Each pair ($L_i, R_i$)is unique.
# output
You need to write a single line containing the minimum cost of the new schedule.
# example
### sample input 1
```
3 1
5 12
2 8
6 15
```
### sample output 1
```
2
```
### sample input 2
```
5 2
3 10
6 13
11 19
2 20
4 8
```
### sample output 2
```
2
```
G- Meetings
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
Ehsan has been invited to Ramtin’s birthday party, where he knows there will be a lot of drinks, food, and games to socialize with friends. Ramtin has a lot of games to play with, but as a good computer teacher, his games are mostly designed to test how good his students are at problem-solving. Often, in these games, one is required to be able to find a solution to a problem and to be quick in doing it.
For fairness sake, Ramtin let Ehsan pick today’s game, and so they all started playing. At the beginning of the game, there is a black box from which every participant randomly picks a string $s_i$ Once every one of the $n$ participants has chosen their string, they have to try to pair them up with each other’s string, attempting to create palindromes while doing so.
More specifically, they can choose any $s_i$ and $s_j$($i \neq j$) and attempt to concatenate them to make a palindrome string. The winner of the game is the fastest person who finds the exact number of ways they can create a palindrome string among all possible pairs.
Help Ehsan win the game by writing an algorithm that, given $n$ unique strings, calculates the number of ways a palindrome string can be constructed!
# input
The first line contains one integer $n$, the number of players. Each of the next $n$ lines contains a string $s_i$, the string chosen by the $i$-th player.
$$2 \leq n \leq 10^4$$
$$1 \leq |s_i| \leq 600$$
+ Each string is unique
+ Each string is always formed by lowercase English letters
# output
You need to write a single line containing the number of ways we can create a palindrome string.
# example
### sample input 1
```
5
abcd
dcba
lls
s
sssll
```
### sample output 1
```
4
```
### sample input 2
```
3
bat
tab
cat
```
### sample output 2
```
2
```
H- Palindromic Match
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
Amin grew tired of the cold and rainy winters in Tabriz. This year, he decided to spend his holidays in Italy, his home country, and to finally visit his favorite amusement park, Pizzalandia.
Pizzalandia, as seen from above, is a rectangle of $X \times Y$ meters (respectively $X$ meters horizontally and $Y$ vertically). Its biggest attraction is without a doubt the Pizzatrain, which runs clockwise along the borders of the rectangle at a fixed speed of 1 meter per second.
Since Amin has already explored most of the park, he thinks it’s finally time for him to get on the train himself, which can be done simply by being on the border of the rectangle at the same second of the train.
He knows the current coordinates of the train, $T_x$ and $T_y$, and he’s currently standing in coordinates $W_x, W_y$. Inside the park, it’s only possible to move horizontally or vertically.
Amin wants to get on the train quickly, but having noticed that today the park is very crowded, he decided that he would simply choose a direction, move in that direction at a speed of 1 meter per second, and then just wait for the train to reach his location.
Help Filippo by figuring out the minimum time it will take him to board the train with this strategy.
# input
This problem has multiple test cases. The first line contains $T$, the number of test cases to solve.
Each of the following $T$ lines contains six integers: the horizontal and vertical lengths of Pizzalandia $X$ and $Y$ , the Pizzatrain’s horizontal and vertical coordinates $𝑇_x$ and $T_y$, and finally Amin’s horizontal and vertical coordinates $W_x$ and $W_y$.
$$1 \leq T \leq 1000$$
$$1 \leq X, Y \leq 10^9$$
$$0 \leq T_x \leq X$$
$$0 \leq T_y \leq Y$$
+ The train is guaranteed to be (and stay!) on the border
$$0 \leq W_x \lt X$$
$$0 \leq W_y \lt Y$$
# output
For each test case, you need to write a single line containing the minimum number of seconds it will take Amin to get on the train, by following his strategy of moving in only one direction.
# example
### sample input 1
```
1
7 6 4 6 3 4
```
### sample output 1
```
5
```
I- Travel to Italy
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
A new Solar Eclipse is going to happen on Mars. Scientists from different parts of the world are traveling to Mars to watch and study this phenomenon. You just managed to calculate exactly the best point of Mars lands for your study of the eclipse, and want to land your flying saucer at that place. But, you notice that there are already other spacecrafts landed near that area.
In the bird’s-eye view, all the spacecrafts (including yours) are circles with a constant radius $R$. Logically, you hate to land your spacecraft on the others (no intersection of areas is allowed, but touching the other crafts is acceptable), though, the other saucers did not obey this rule on their own landings (i.e. their circles might have positive-area intersections with each other). In order to land your own craft on Mars, you want to find the place that minimizes the distance between the center of your flying saucer and your already calculated best point (and obeys the no-intersection rule). That’s what you should do in this problem.
# input
The input has multiple test cases. Each test case starts with a line containing an integer $n$ (number of already landed spacecrafts), and a real number $r$.The land is small enough for us to be modeled by a two-dimensional plane, and $(0, 0)$ is conventionally the best point for us to land. Each of the next $n$ lines specifies the location of a landed flying saucer by giving two real numbers, $x$ and $y$ as the coordinates of its center. The input ends with a case of $n = r = 0$ which must not be processed.
$$1 \leq n \leq 100$$
$$0 \lt R$$
$$0 \leq |x|, |y| \leq 1000$$
# output
Write the result of the $i$-th test case on the $i$-th line of the output. You should just write the minimum possible distance between the center of your landed craft and the origin of the plane, rounded to **exactly** 6 digits after the decimal point.
# example
### sample input 1
```
1 1.234
2.468 0
1 2
2 2
2 1
1 1
-1 -1
0 0
```
### sample output 1
```
0.000000
1.171573
1.414214
```
J- Solar Eclipse
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
Saman loves brackets (or parentheses). He calls a sequence of ‘(’ and ‘)’ characters a “valid bracket sequence” if either:
+ It’s an empty sequence, or
+ For each open bracket, we can find a closed bracket on its right such that the substring
between these two brackets forms a valid bracket sequence, and such that after removing that substring, the remaining brackets also form a valid bracket sequence.
For example, `(())` and `()()` are both valid, while `)(` and `())(()` are not.
Furthermore, he calls a string of parentheses “$k$-valid” if, f, after adding $k$ open brackets to its left and $k$ closed brackets to its right, it is valid (either because it was valid before, or because it became valid). For example `)(` and `())(()` are both $1$-valid, while `))((` is 2-valid.
Saman is curious to find for any given $n$ and $k$ how many bracket sequences there are with length $2n$ that are $k$-valid. Because the result may be very large, Saman is only interested in its remainder after dividing it by $10^9 + 7$.
Help Saman by writing a program that quickly calculates this number for $Q$ different queries.
# input
The first line contains one integer $Q$, the number of queries Saman is interested in.
The next $Q$ lines contain each a pair of integers $n_i$ and $k_i$.
$$1 \leq n \leq 10^5$$
$$1 \leq n_i, k_i \leq 10^6$$
# output
You need to write $Q$ lines containing each the result of the $i$-th query: for each query, print the number of strings of length $2n_i$ that are $k_i$-valid, modulo $10^9 + 7$
# example
### sample input 1
```
3
2 1
4 2
5 3
```
### sample output 1
```
5
62
242
```