• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

شکارچی گنج‌ها در دنیای کدکاپ شنیده که در یک نقطه از فضای سه بعدی کدکاپ، گنجی وجود دارد که این نقطه بر روی گوشه‌ یک مکعب مستطیل قرار دارد.

در فضای سه‌بعدی کدکاپ یک مکعب‌مستطیل، وجود دارد که وجه‌های آن موازی محورهای مختصات است. این مکعب‌مستطیل مانند هر مکعب‌مستطیل دیگری در دنیای کدکاپ، ۸ نقطه در گوشه‌ها دارد. مختصات یکی از نقطه‌ها گم‌ شده است و همه معتقدند که گنج در آن نقطه قرار دارد. با گرفتن مختصات ۷ نقطه‌ی دیگر این مکعب مستطیل، مختصات نقطه ای که گنج در آن قرار دارد را به شکارچی گنج‌ها بگویید.

ورودی🔗

ورودی شامل ۷ خط است و در هر خط ۳ عدد آمده است.

در خط $i$ از ورودی سه عدد $x_i$ و $y_i$ و $z_i$ آمده است که نشانگر مختصات یکی از گوشه‌های مکعب‌مستطیل است.

$0 \leq x_i, y_i, z_i \leq 1000 \, 000$

خروجی🔗

خروجی برنامه‌ی شما باید شامل یک خط باشد که در آن سه عدد $x$ و $y$ و $z$ مختصات گوشه‌ی گم‌شده را نشان دهد.

مثال‌ها🔗

ورودی نمونه ۱🔗

0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0

خروجی نمونه ۱🔗

1 1 1

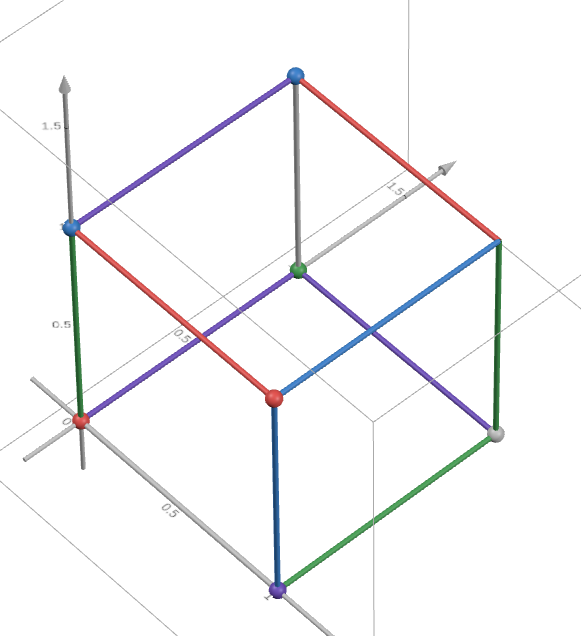
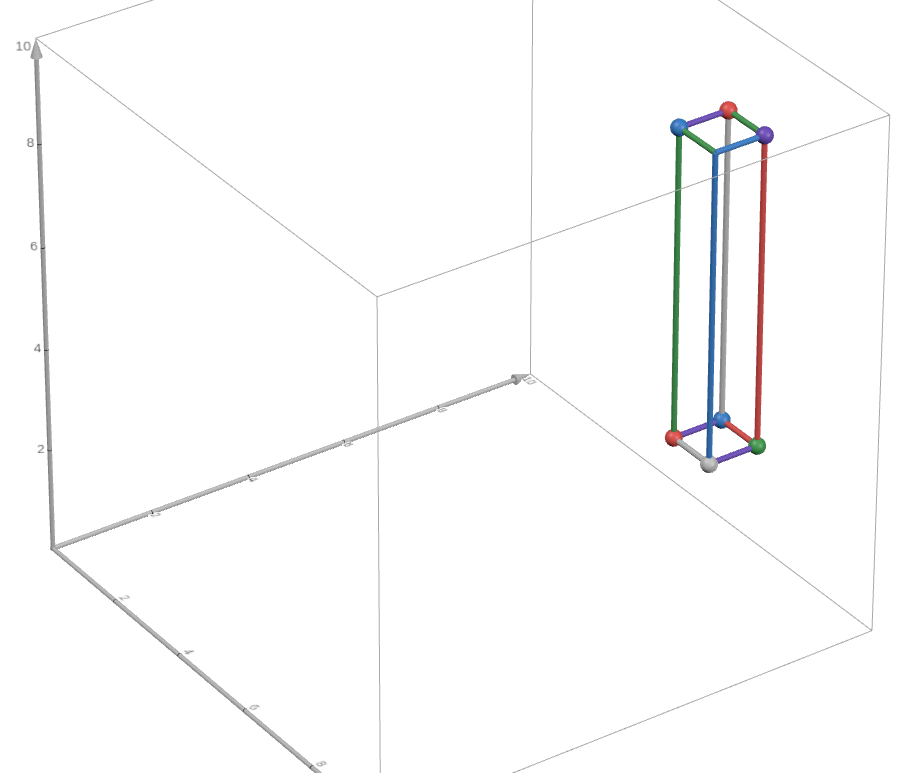
ورودی نمونه ۲🔗

7 9 9
7 9 3
8 9 3
8 9 9
8 8 3
7 8 3
7 8 9

خروجی نمونه ۲🔗

8 8 9

if 1 <= n <= 100:
    # answer of problem
else:
    # print('invalid input')

input('please enter:')

package ir.quera.contest;

• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

یک صفحه‌ی شطرنجی $n \times m$ را در نظر بگیرید. سطرهای آن را از بالا به پایین با اعداد $1$ تا $n$ و ستون‌های آن را از چپ به راست با اعداد $1$ تا $m$ شماره‌گذاری می‌کنیم. خانه‌ی سطر $i$ام و ستون $j$ام از این جدول را به صورت زوج مرتب $(i, j)$ نشان می‌دهیم.

دو نوع مهره داریم «ربع فیل شمال غربی» و «ربع فیل جنوب شرقی» که به ترتیب با دو حرف A و B نشان می‌دهیم.

• اگر یک مهره‌ی نوع A در خانه‌ی $(i, j)$ جدول قرار بگیرد، همه‌ی خانه‌های $(i - 1, j - 1)$، $(i - 2, j - 2)$ و... را در صورت وجود تهدید می‌کند.

• اگر یک مهره‌ی نوع B در خانه‌ی $(i, j)$ جدول قرار بگیرد، همه‌ی خانه‌های $(i + 1, j + 1)$، $(i + 2, j + 2)$ و... را در صورت وجود تهدید می‌کند.

حال می‌خواهیم در هر خانه از این جدول حداکثر یک ربع فیل از نوع A یا B قرار دهیم به طوری که هیچ دوتایی یکدیگر را تهدید نکنند.

از شما می‌خواهیم چیدمانی از این مهره‌ها را در جدول قرار دهید، که حداکثر تعداد مهره استفاده شود. به عبارت دیگر می‌خواهیم تعداد خانه‌های خالی جدول کمینه باشد. (بنابراین مجموع تعداد مهره‌های نوع A و B باید بیشینه باشد و تعداد هر کدام لزومی ندارد ماکسیمم باشد.)

اگر چند حالت برای رسیدن به جواب وجود دارد یکی را به دلخواه چاپ کنید.

ورودی🔗

در تنها سطر ورودی، دو عدد صحیح و مثبت $n$ و $m$ داده می‌شود که به ترتیب تعداد سطرها و ستون‌های جدول را نشان می‌دهد.

$1 \leq n, m \leq 100$

خروجی🔗

در $n$ سطر و در هر سطر $m$ کاراکتر چاپ کنید. کاراکتر $j$ام در سطر $i$ام جواب وضعیت $(i, j)$ را نشان می‌دهد.

اگر آن خانه خالی بود .، اگر مهره‌ی نوعA بود A و در غیر این‌صورت B را چاپ کنید. توجه کنید هر جواب درستی، قابل قبول است.

مثال‌ها🔗

ورودی نمونه ۱🔗

3 4

خروجی نمونه ۱🔗

.AAB
AABB
BBB.

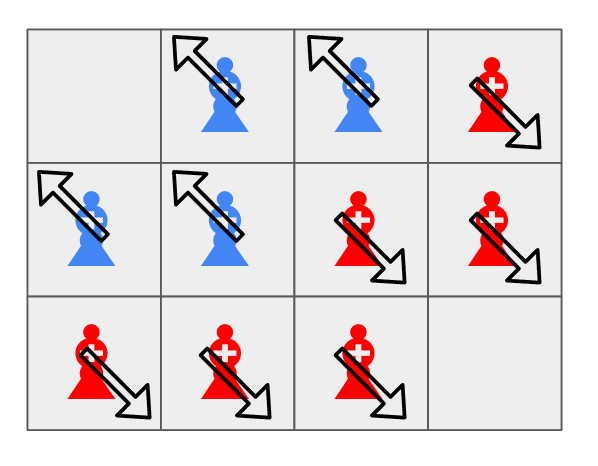
ورودی نمونه ۲🔗

2 5

خروجی نمونه ۲🔗

AAAAA
BBBBB

• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

در یک مهمانی $n$ عدد کیک با اندازه برابر داریم. $k$ مهمان به این مهمانی می‌آیند و میزبان می‌خواهد کیک‌ها را طوری تقسیم کند که به هر مهمان مقدار برابری کیک برسد و هیچ کیکی باقی نماند.

روش تقسیم کیک‌ها به این صورت است که در هر مرحله میزبان تعداد دلخواهی قطعه کیک را انتخاب می‌کند و همه را به دو قسمت برابر تقسیم می‌کند.

از آن‌جا که میزبان سرش حسابی شلوغ است از شما خواسته است که در تقسیم کیک‌ها را به او کمک کنید و به او بگویید که اصلا این کار امکان‌پذیر است یا خیر و اگر امکان‌پذیر هست حداقل چند مرحله تقسیم باید انجام شود.

ورودی🔗

در خط اول ورودی ابتدا عدد $t$ که نشان‌دهنده‌ی تعداد مهمانی‌های برگزار شده، آمده‌است.

$1 \le t \le 100 \, 000$

سپس در $t$ خط بعدی، در هر خط دو عدد $n$ و $k$ به ترتیب داده می‌شوند که اولی نشان‌دهنده‌ی تعداد کیک‌های اولیه و دومی تعداد مهمان‌ها است. $1 \le n, k \le 10^9$

خروجی🔗

برای هر مهمانی اگر تقسیم کیک امکان‌پذیر بود، کم‌ترین تعداد برش لازم و در غیر این صورت عدد -1 را در یک خط به عنوان خروجی چاپ کنید.

مثال🔗

ورودی نمونه ۱🔗

3
10 3
4 8
7 16

خروجی نمونه ۱🔗

-1
1
4

سناریو اول. در سناریو اول $n = 10$ کیک و $k = 3$ مهمان داریم. پس باید به هر مهمان اندازه‌ی $\frac{10}{3} = 3.333\cdots$ برابر یک کیک کامل برسد. هر بار می‌توانیم فقط قطعات کیک را نصف کنیم پس هیچ وقت نمی‌توانیم با تعدادی برش و برداشتن چند قطعه به این عدد برسیم.

سناریو دوم. در سناریو اول $n = 4$ کیک و $k = 8$ مهمان داریم. پس باید به هر مهمان اندازه‌ی $\frac{4}{8} = 0.5$ برابر یک کیک کامل برسد. پس می‌توانیم با یک عملیات همه‌ی کیک‌ها را نصف کنیم و به هر مهمان یک قطعه بدهیم.

سناریو سوم. در سناریو اول $n = 7$ کیک و $k = 16$ مهمان داریم. پس باید به هر مهمان اندازه‌ی $\frac{7}{16} = 0.4375$ برابر یک کیک کامل برسد. پس می‌توانیم با چهار عملیات هر کیک را به ۱۶ قسمت تقسیم کنیم (هر بار همه قطعات را کنار هم می‌گذاریم و با یک عملیات همه را نصف می‌کنیم.) سپس به هر مهمان ۷ قطعه کیک می‌دهیم.

• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

منظور از مشق یک مجموعه $k$ عضوی جمع $\lfloor\frac{k}{2}\rfloor$ عضو بزرگ‌تر منهای $\lceil\frac{k}{2}\rceil$ عضو کوچک‌تر آن است. برای مثال مشق مجموعه‌ی $\{2, 3, 7\}$ برابر $7-3-2=2$ و مشق مجموعه‌ی ${1, 2, 3, 4}$ برابر $4 + 3 - 2 - 1 = 4$ است. مشق مجموعه‌ی تهی را صفر در نظر بگیرید.

اعضای یک مجموعه‌ی $n$ عضوی از اعداد صحیح را داریم، می‌خواهیم به ازای تمام $2^n$ زیرمجموعه ممکن از این مجموعه، مشق آن‌ها را با هم جمع کنیم. از شما می‌خواهیم برنامه‌ای بنویسید که این مقدار را حساب کند. (برای بهتر متوجه شدن سوال، مثال اول را مطالعه کنید.)

چون ممکن است حاصل خیلی بزرگ باشد، باقی‌مانده‌ی پاسخ را بر $10^9 + 7$ محاسبه کنید.

ورودی🔗

در خط اول عدد $n$ و سپس در خط بعد $n$ عدد صحیح $a_i$ با فاصله از هم ورودی داده می‌شوند.

$1 \le n \le 5000$ $1 \le a_i \le 1000 \, 000$

تضمین می‌شود که $a_1 \lt a_2 \lt \dots \lt a_n\,$ باشد.

خروجی🔗

حاصل جمع مورد نظر را خروجی دهید.

مثال🔗

ورودی نمونه ۱🔗

4
1 2 3 7

خروجی نمونه ۱🔗

22

$\begin{array}{ccc} \{\} & \to & 0 \\ \{ 2 \} & \to & -2 \\ \{ 7 \} & \to & -7 \\ \{ 1 \} & \to & -1 \\ \{ 3 \} & \to & -3 \\ \{ 2, 7 \} & \to & 7 - 2 = 5 \\ \{ 1, 2 \} & \to & 2 - 1 = 1 \\ \{ 2, 3 \} & \to & 3 - 2 = 1 \\ \{ 1, 7 \} & \to & 7 - 1 = 6 \\ \{ 3, 7 \} & \to & 7 - 3 = 4 \\ \{ 1, 3 \} & \to & 3 - 1 = 2 \\ \{ 1, 3, 7 \} & \to & 7 - 3 - 1 = 3\\ \{ 1, 2, 3 \} & \to & 3 - 2 - 1 = 0 \\ \{ 2, 3, 7 \} & \to & 7 - 3 - 2 = 2 \\ \{ 1, 2, 7 \} & \to & 7 - 2 - 1 = 4 \\ \{ 1, 2, 3, 7 \} & \to & 7 + 3 - 2 - 1 = 7\\ \end{array}$

بنابراین حاصل جمع برابر است با: $0 - 2 - 7 -1 -3 + 5 + 1 + 1 + 6 + 4 + 2 + 3 + 0 + 2 + 4 + 7 = 22$

ورودی نمونه ۲🔗

3
1 2 3

خروجی نمونه ۲🔗

1000000005

$\begin{array}{ccc} \{\} & \to & 0 \\ \{ 1 \} & \to & -1 \\ \{ 2 \} & \to & -2 \\ \{ 3 \} & \to & -3 \\ \{ 1, 2 \} & \to & 2 - 1 = 1\\ \{ 1, 3 \} & \to & 3 - 1 = 2 \\ \{ 2, 3 \} & \to & 3 - 2 = 1 \\ \{ 1, 2, 3 \} & \to & 3 - 2 - 1 = 0 \\ \end{array}$

بنابراین حاصل جمع برابر است با: $0 - 1 -2 -3 + 1 + 2 + 1 + 0 = -2$

توجه کنید باقی‌مانده‌ی $-2$ بر $1000,000,007$ برابر $1000,000,005$ است.

• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

نقشه‌ی کشور احسان شامل $n$ شهر است که با $m$ جاده به هم متصل شده‌اند. احسان که خیلی از تجزیه‌ی کشور به دست انقلابیون می‌ترسد، می‌خواهد میزان مقاومت نقشه به تجزیه را بررسی کند. می‌گوییم کشور در معرض تجزیه است اگر جاده‌ای وجود داشته باشد که با حذفش، تمامی شهرهای یک بخش توسط شورشی‌ها تصرف شده باشند. از بین تمام $2^n$ حالتی که شورشی‌ها می‌توانند تعدادی از شهرها را تصرف کرده باشند، تعداد حالاتی را می‌خواهیم بدانیم که کشور در معرض تجزیه نباشد.

باقی‌مانده این عدد را به $10^9+7$ چاپ کنید.

ورودی🔗

خط اول ورودی تنها شامل دو عدد طبیعی $n$ و $m$ است که با فاصله از هم آمده‌اند. در $m$ خط بعدی، در هر خط دو عدد طبیعی آمده است که نشان دهنده‌ی دو شهری است که این جاده به هم متصل می‌کند. $1 \le n \le 100 \, 000$ $1 \le m \le 300 \, 000$

تضمین می‌شود از هر شهر با استفاده از جاده‌ها می‌توان به هر شهر دیگر سفر کرد همچنین هیچ جاده‌ای یک شهر را به خودش متصل نمی‌کند و بین هیچ دو شهری بیش از یک جاده وجود ندارد.

خروجی🔗

باقی‌مانده‌ی تعداد حالاتی که کشور در معرض تجزیه نیست را به $10^9+7$ چاپ کنید.

ورودی نمونه ۱🔗

3 2
1 2
2 3

خروجی نمونه ۱🔗

2

در این تصویر دو حالتی را که کشور در معرض تجزیه نیست را می‌بینیم.

ورودی نمونه ۲🔗

4 4
1 2
2 3
3 1
1 4

خروجی نمونه ۲🔗

7

• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

علی مدیر یک پروژه پل‌سازی است که به پایانش نزدیک شده است. در این پروژه ابتدا $n$ پایه بتنی بر روی زمین ساخته شده است، به طوری که پایه‌ی $i$ام در مکان $x_i$ قرار دارد. برای تکمیل پروژه باید مسیر بین پایه‌ی اول ($x_1$) و پایه‌ی آخر ($x_n$) با تعدادی تخته‌‌چوبی به طول $T$ به هم متصل شوند. طبق قوانین پل‌سازی، زیر هر تخته‌چوب باید حداقل $k$ پایه‌ی بتنی وجود داشته باشد، تا تخته‌چوب، سفت در جای خود قرار بگیرد. علی می‌خواهد بداند به ازای تمام $k$های بین $1$ و $n$ در صورتی که می‌توان پل را ساخت، به حداقل چند تخته‌چوب نیاز دارد.

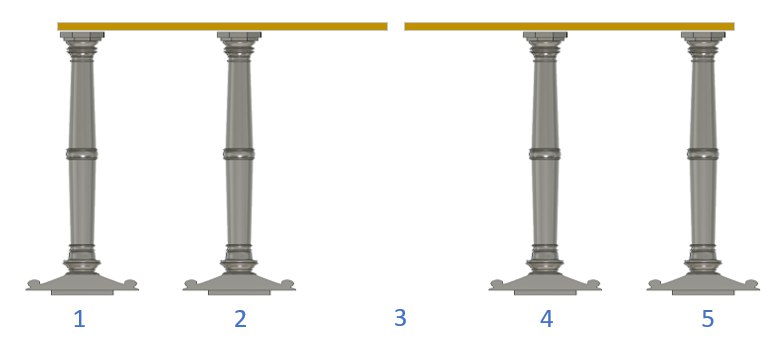
در تصویر بالا جواب مسئله برای $k=2$ برای تست اول نشان داده شده است.

توجه کنید عرض ستون‌ها را صفر در نظر می‌گیریم. فرض کنید یک تخته‌چوب یک بازه‌ی بسته مثل $[x, x + T]$ را متصل می‌کند و ستون‌های شامل این بازه، زیر آن در نظر گرفته می‌شود. شما باید بازه‌ی $[x_1, x_n]$ را متصل کنید و ممکن است تخته چوب‌ها اشتراک داشته باشند.

ورودی🔗

در خط اول ورودی دو عدد طبیعی $n$ و $T$ با فاصله از هم آمده‌ است.

$1 \le n \le 100 \, 000$ $1 \le T \le 10^9$

در خط دوم ورودی $n$ عدد آمده است که مکان پایه‌های بتنی پل را نشان می‌دهد. عدد $i$ام آن برابر $x_i$ است. $0 \le x_i \le 10^9$

تضمین می‌شود که $x_1 \lt x_2 \lt \dots \lt x_n\,$ باشد.

خروجی🔗

در تنها خط خروجی، $n$ عدد خروجی دهید که نشان‌دهنده‌ی جواب مسئله، به ترتیب به ازای $k$های $1$ تا $n$ باشد و اگر ساختن پل ممکن نبود، به‌جای تعداد تخته‌چوب‌ها -1 چاپ کنید.

ورودی نمونه ۱🔗

4 2
1 2 4 5

خروجی نمونه ۱🔗

2 2 -1 -1 

ورودی نمونه ۲🔗

4 10
0 1 2 20

خروجی نمونه ۲🔗

2 -1 -1 -1