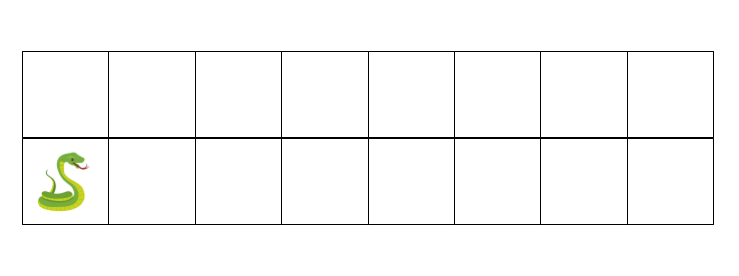
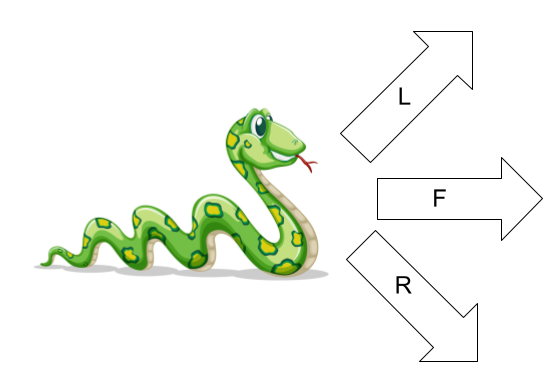
+ محدودیت زمان: ۱ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- در شهر کدکاپ، مارها بدن‌های بسیار طولانی دارند و در تونل‌هایی به شکل جدول ۸ $\times$ ۲ زندگی می‌کنند. یک مار کدکاپی مانند شکل زیر در خانه‌ی پایین چپ این جدول قرار دارد به طوری که سر این مار به سمت انتهای تونل (سمت راست تصویر) است.  هر بار این مار یکی از ۳ حرکت زیر را انجام می‌شود: + حرکت `F`: در همان سطری که هست به خانه روبه‌رو می‌رود. + حرکت `L`: در سطر سمت چپ خودش به خانه روبه‌رو می‌رود. + حرکت `R`: در سطر سمت راست خودش به خانه روبه‌رو می‌رود.  اگر سر این مار به خانه‌ای برود که در جدول وجود ندارد، محکم به دیوار می‌خورد و می‌میرد. به شما حرکت‌های مار داده می‌شود، از شما می‌خواهیم وضعیت بدن مار را بعد از همه‌ی آن حرکت‌ها مشخص کنید یا بگویید که مار می‌میرد. برای بهتر متوجه شدن سوال، به توضیحات نمونه‌ها مراجعه کنید. # ورودی یک رشته به طول ۷ با کاراکترهای `F`، `L` یا `R` که نشان دهنده‌ی حرکت مار به مستقیم، چپ یا راست است. # خروجی دو رشته به طول ۸ شامل ۰ و ۱ که ۱ نشان دهنده‌ی حضور مار در آن خانه و ۰ نشان دهنده‌ی خالی بودن آن خانه باشد که در دو خط چاپ می‌شوند. 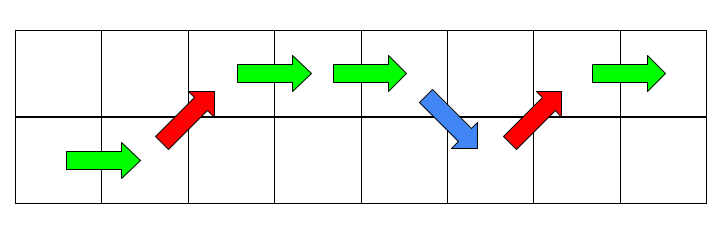# مثال‌ها ## ورودی نمونه ۱ ``` FLFFRLF ```` ## خروجی نمونه ۱ ``` 00111011 11000100 ```` <details> <summary> **توضیح نمونه ۱** </summary> ---------- مسیر حرکت مار به صورت زیر است.  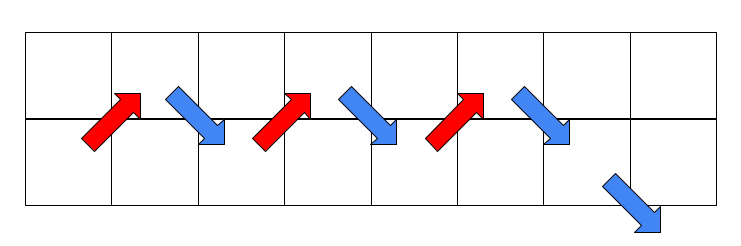---------- </details> ## ورودی نمونه ۲ ``` LRLRLRR ```` ## خروجی نمونه ۲ ``` DEATH ```` <details> <summary> **توضیح نمونه ۲** </summary> ---------- بعد از انجام آخرین حرکت، سر مار به دیوار می‌خورد و می‌میرد. (چون در ستون پایینی است و نمی‌تواند پایین‌تر به راست برود.)  ---------- </details> <details class="red"> <summary> **اشتباهات متداول** </summary> <details class="red"> <summary> **چک کردن شرایط ورودی مسئله** </summary> نیازی نیست چک کنید شرایط گفته شده در ورودی برقرار است یا نه. توضیحات محدودیت‌ها فقط برای آگاهی شما درباره‌ی تست‌ها و محدودیت‌های مسئله است و قطعاً در ورودی‌های داده شده به برنامه‌ی شما رعایت می‌شوند. پس نیازی نیست بنویسید: ```python if 1 <= n <= 100: # answer of problem else: # print('invalid input') ``` </details> <details class="red"> <summary> **ابتدا همه‌ی ورودی را گرفتن و در نهایت همه‌ی خروجی را چاپ کردن** </summary> شما می‌توانید لابه‌لای دریافت ورودی، خروجی دهید. پس نیازی نیست ابتدا همه‌ی ورودی‌ها را دریافت کنید و در نهایت همه‌ی خروجی‌ها را چاپ کنید. مخصوصاً برای سوالاتی که باید به چندین سوال پاسخ دهید، می‌توانید دو قسمت ورودی و خروجی را کاملاً مستقل در نظر بگیرید و مطمئن باشید تداخلی پیش نمی‌آید. </details> <details class="red"> <summary> **چاپ کردن موارد اضافه برای دریافت ورودی** </summary> لطفاً از چاپ کردن موارد اضافه مثل `please enter a number` برای دریافت ورودی پرهیز کنید. برای مثال در زبان پایتون نباید بنویسید: ```python input('please enter:') ``` </details> <details class="red"> <summary> **چند فایلی کد زدن** </summary> برای زبان‌هایی مثل جاوا نباید در بالای کد شما آدرس پکیج داده شود. برای مثال در بالای کد خود نباید بنویسید: ```java package ir.quera.contest; ``` </details> <details class="red"> <summary> **استفاده از چند `Scanner` برای دریافت ورودی** </summary> در زبان جاوا، باید فقط یک شئ از جنس `Scanner` تعریف کنید و همه‌ی ورودی‌ها را با آن دریافت کنید. </details> <details class="red"> <summary> **نحوه‌ی دریافت ورودی و چاپ کردن خروجی** </summary> برای آشنایی بیشتر برای نحوه‌ی دریافت ورودی و چاپ کردن خروجی این [لینک](https://quera.org/course/assignments/2693/problems/8774) را مطالعه کنید. </details>

+ محدودیت زمان: ۱ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- در کشور کدکاپ قدیم $n$ شهر با شماره‌های ۱ تا $n$ وجود داشته است. این کشور $n - 1$ جاده دو طرفه داشت و هر جاده دقیقاً دو شهر را به هم متصل می‌کرد. می‌دانیم در کدکاپ قدیم از هر شهری به هر شهر دیگر یک مسیر وجود داشته است (در واقع نقشه‌ی کشور کدکاپ به صورت یک [درخت](https://fa.wikipedia.org/wiki/%D8%AF%D8%B1%D8%AE%D8%AA_%28%D9%86%D8%B8%D8%B1%DB%8C%D9%87_%DA%AF%D8%B1%D8%A7%D9%81%29) بوده است). منظور از یک *مسیر*، دنباله‌ای از شهرهای **مختلف** مثل $v_1, v_2, \dots, v_k\,$ است؛ به‌طوری که هر دو شهر متوالی با یک جاده به هم متصل شده باشد. طول این مسیر را $k$ می‌نامیم. منظور از بلندترین مسیر کشور، مسیری است که بین همه‌ی مسیرهای ممکن، بلندترین طول دارد. اما اکنون نقشه‌ی کشور کدکاپ را از دست دادیم و برای هر شهر، تعداد جاده‌هایی که از آن خارج شده را می‌دانیم. می‌خواهیم با توجه به این عددها در بین تمام نقشه‌های ممکن برای کدکاپ قدیم، نقشه‌ای را در نظر بگیریم که طول بلندترین مسیر آن بیشینه است. از شما می‌خواهیم این طول را حساب کنید. # ورودی در اولین خط ورودی عدد $n$ که نشان دهنده تعداد شهرهای کدکاپ قدیم داده می‌شود. $$2 \leq n \leq 1 \, 000 \, 000$$ سپس در خط بعد $n$ عدد $d_i$ با فاصله از هم داده می شوند که عدد $i$ام یعنی $d_i$ نشان دهنده تعداد جاده‌های خارج شده از شهر $i$ است. $$1 \leq d_i \leq n - 1$$ تضمین می‌شود از روی دنباله‌ی داده شده، حداقل یک نقشه برای کدکاپ قدیم می‌توان ساخت. # خروجی شما باید در یک خط، طول بلندترین مسیر در نقشه‌ی کدکاپ قدیم را چاپ کنید. 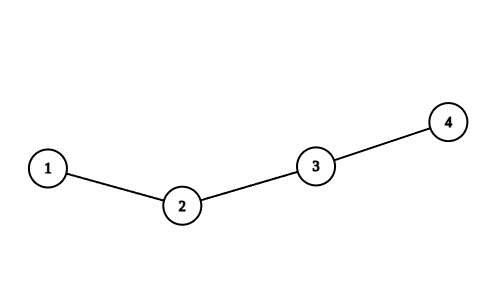# مثال‌ها ## ورودی نمونه ۱ ``` 4 1 2 2 1 ``` ## خروجی نمونه ۱ ``` 4 ``` <details> <summary> **توضیح نمونه ۱** </summary> ---------- نقشه‌ی کدکاپ قدیم می‌تواند به صورت زیر باشد، تا تعداد جاده‌های خارج شده از هر شهر دقیقاً برابر اعداد ورودی باشد. بلند‌ترین مسیر آن $\langle 1, 2, 3, 4 \rangle$ است که طول آن ۴ است و این حداکثر مقدار ممکن است.  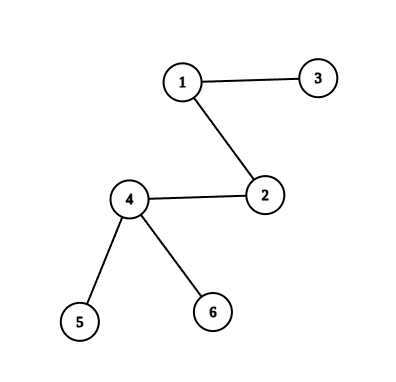---------- </details> ## ورودی نمونه ۲ ``` 6 2 2 1 3 1 1 ``` ## خروجی نمونه ۲ ``` 5 ``` <details> <summary> **توضیح نمونه ۲** </summary> ---------- یکی از بلند‌ترین مسیرهای آن $\langle 3, 1, 2, 4, 5 \rangle$ است که طول آن ۵ است. و بین تمام حالت‌های قابل قبول دیگر برای نقشه‌ی کدکاپ قدیم، این مثال بیشترین طول را برای بلندترین مسیر دارد.  ---------- </details>

+ محدودیت زمان: ۱ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- در شهر کدکاپ‌آباد تنها یک خط مترو وجود دارد که هر روز تنها یک بار از ایستگاه ۱ شروع کرده و تا ایستگاه آخر می‌رود. $n$ ساکن این شهر هر روز صبح برای رفتن به سر کار از این خط مترو استفاده می‌کنند. شهروند $i$ام اول صبح می‌خواهد از ایستگاه $s_i$ به ایستگاه $e_i$ برود. قطار شهر کدکاپ‌آباد بسیار قدیمی است و حداکثر $L$ نفر می‌توانند سوار آن شوند. هر فرد می‌تواند در ایستگاه $s_i$ سوار قطار شود و در یکی از ایستگاه‌های ادامه‌ی مسیر پیاده شود و باقی مسیر را پیاده برود. اگر شهروند $i$ام در ایستگاه $m_i$ از قطار پیاده شود باید $\mid m_i-e_i \mid$ واحد پیاده برود. زمان پیاده شدن هر شهروند از قطار طوری تعیین کنید که مجموع میزان پیاده روی شهروندان کمینه شود. (توجه کنید که $m_i$ می‌تواند برابر با $s_i$ باشد. یعنی شما می‌توانید یکی از شهروندان را اصلاً سوار قطار نکنید.) # ورودی در سطر اول ورودی، دو عدد صحیح و مثبت $n$ و $L$ آمده است که $n$ نشان دهنده‌ی شهروندان شهر کدکاپ‌آباد و $L$ نشان دهنده‌ی حداکثر تعداد مسافر سوار بر قطار است. $$1 \leq n, L \leq 100 \, 000$$ در هر کدام از $n$ سطر بعدی، در سطر $i$ام $s_i$ و $e_i$ آمده است که نشان دهنده‌ی مبدا و مقصد شهروند $i$ ام است. $$1 \leq s_i \lt e_i \leq 300 \, 000$$ # خروجی کمینه‌ی مجموع خستگی شهروندان را چاپ کنید. 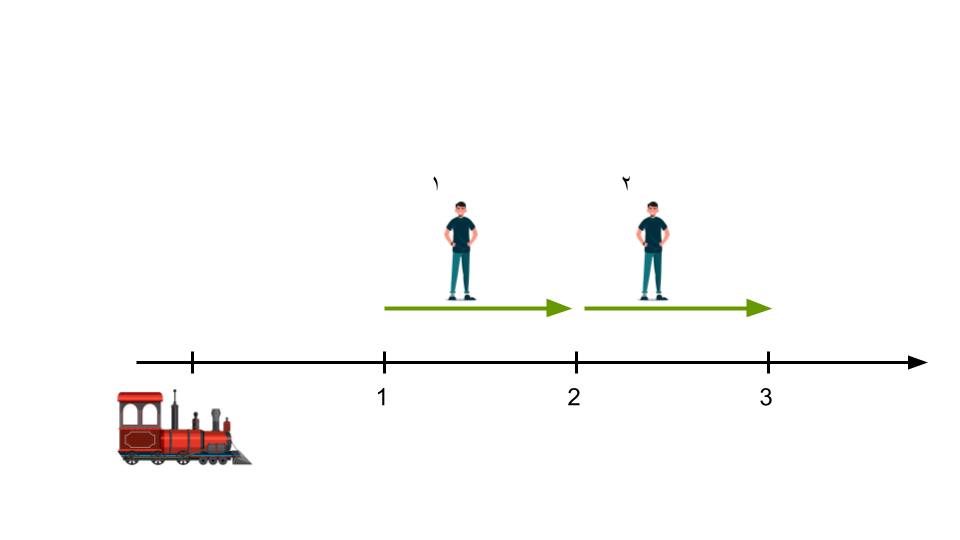# مثال‌ها ## ورودی نمونه ۱ ``` 2 1 1 2 2 3 ```` ## خروجی نمونه ۱ ``` 0 ```` <details> <summary> **توضیح نمونه ۱** </summary> ----------  + در ایستگاه ۱ مسافر ۱ را سوار می‌کند. + در ایستگاه ۲ مسافر ۱ را پیاده می‌کند و مسافر ۲ را سوار می‌کند. + در ایستگاه ۳ مسافر ۲ را پیاده می‌کند. به این ترتیب هر دو مسافرها در مقصدی که می‌خواهند پیاده می‌شوند. پس مجموع خستگی‌ها $0 + 0 = 0$ می‌شود. 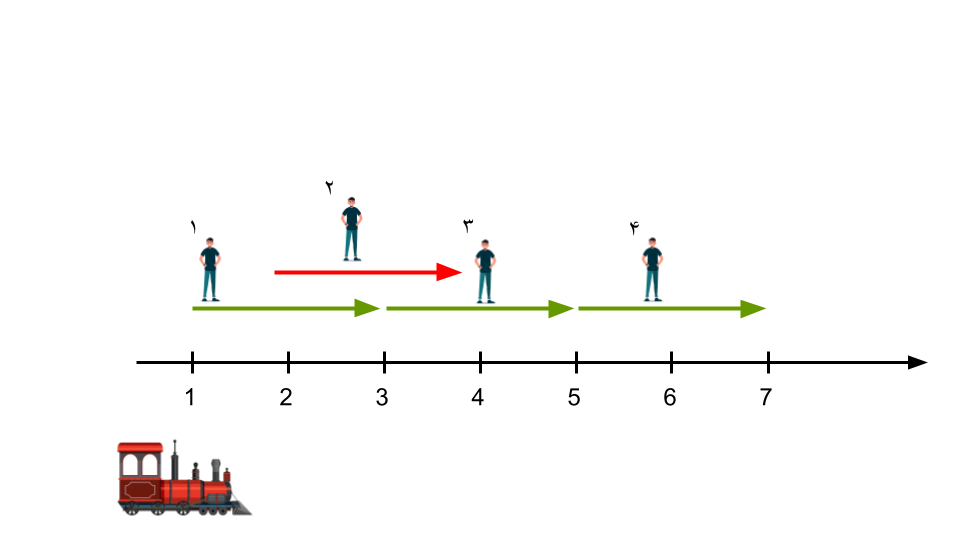---------- </details> ## ورودی نمونه ۲ ``` 4 1 1 3 2 4 3 5 5 7 ```` ## خروجی نمونه ۲ ``` 2 ```` <details> <summary> **توضیح نمونه ۲** </summary> ----------  + در ایستگاه ۱ مسافر ۱ را سوار می‌کند. + در ایستگاه ۳ مسافر ۱ را پیاده می‌کند و مسافر ۳ را سوار می‌کند. + در ایستگاه ۵ مسافر ۳ را پیاده می‌کند و مسافر ۴ را سوار می‌کند. + در ایستگاه ۷ مسافر ۴ را پیاده می‌کند. به این ترتیب مسافرهای ۱، ۳ و ۴ در مقصدی که می‌خواهند پیاده می‌شوند ولی مسافر ۲ اصلاً سوار نشده و باید پیاده به مقصدش برود و به‌اندازه‌ی $\mid 4 - 2 \mid = 2$ خسته می‌شود. پس مجموع خستگی‌ها $0 + 2 + 0 + 0 = 2$ می‌شود. 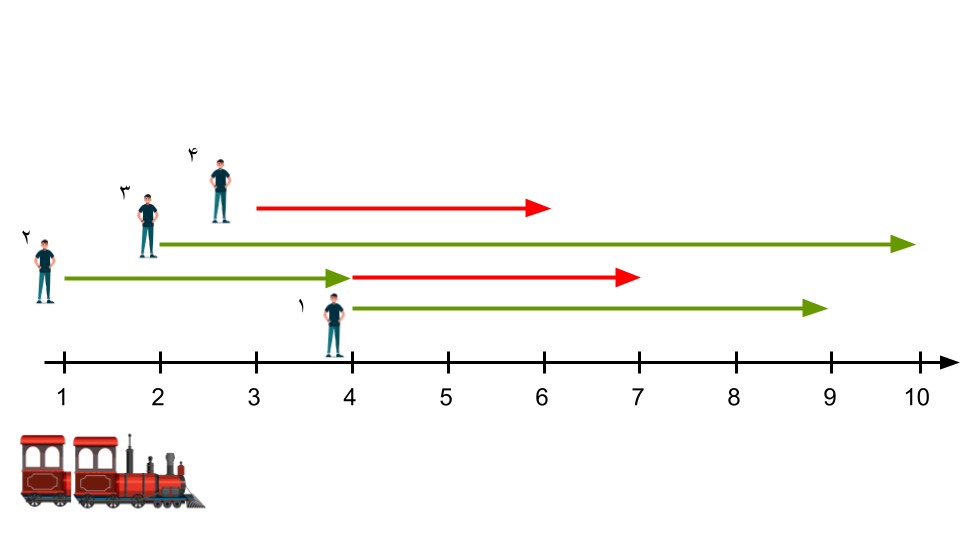---------- </details> ## ورودی نمونه ۳ ``` 4 2 4 9 1 7 2 10 3 6 ```` ## خروجی نمونه ۳ ``` 6 ```` <details> <summary> **توضیح نمونه ۳** </summary> ----------  + در ایستگاه ۱ مسافر ۲ را سوار می‌کند. + در ایستگاه ۲ مسافر ۳ را سوار می‌کند. (توجه کنید اینبار ۲ نفر ظرفیت دارد.) + در ایستگاه ۴ مسافر ۲ را پیاده می‌کند و مسافر ۱ را سوار می‌کند. + در ایستگاه ۹ مسافر ۱ را پیاده می‌کند. + در ایستگاه ۱۰ مسافر ۳ را پیاده می‌کند. به این ترتیب مسافرهای ۱ و ۳ در مقصدی که می‌خواهند پیاده می‌شوند ولی مسافر ۴ اصلاً سوار نشده و باید پیاده به مقصدش برود و به‌اندازه‌ی $\mid 6 - 3 \mid = 3$ خسته می‌شود. همچنین مسافر ۲ در ایستگاه ۴ پیاده شده ولی می‌خواست به ایستگاه ۷ برود و به‌اندازه‌ی $\mid 7 - 4 \mid = 3$ خسته می‌شود. پس مجموع خستگی‌ها $0 + 3 + 0 + 3 = 6$ می‌شود. ---------- </details>

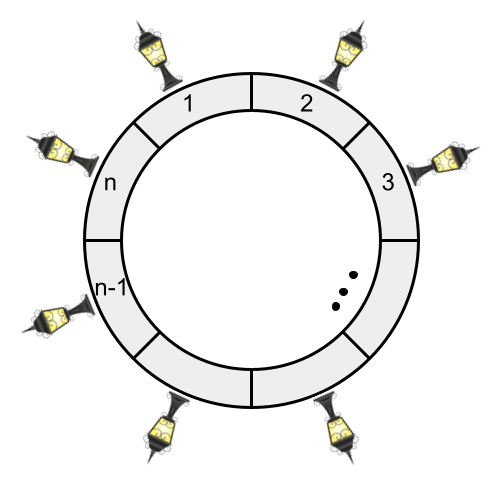
+ محدودیت زمان: ۱ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- میدان اصلی شهر کدکاپ بسیار بزرگ است. دور این میدان $n$ چراغ روشنایی قرار دارد. این چراغ‌ها را با اعداد ۱ تا $n$ به ترتیب ساعت‌گرد شماره‌گذاری کرده‌اند.  می‌دانیم اگر یک چراغ روشن شود، محوطه زیر آن و دو چراغ مجاورش روشن می‌شود. به صورت رسمی‌تر اگر چراغ شماره‌ی $i$ را روشن کنیم، ($1 \leq i \leq n$) محوطه‌ی زیر چراغ $i$، $i - 1$ و $i + 1$ روشن می‌شود. (اگر $i + 1$ از $n$ بیشتر شد به‌جای آن ۱ و اگر $i - 1$ از ۱ کمتر شد به‌جای آن $n$ را در نظر بگیرید.) می‌دانیم هزینه‌ی روشن کردن شماره‌ی $i$ برابر $c_i$ است. می‌خواهیم با کمترین هزینه ممکن، تعدادی از چراغ‌ها را روشن کنیم به طوری که محوطه‌ی زیر همه‌ی چراغ‌ها روشن باشد. # ورودی در سطر اول عدد $t$ آمده که تعداد تست‌ها را نشان می‌دهد. $$1 \leq t \leq 200 \, 000$$ در هر خط یک عدد $n$ و سپس در خط بعد $n$ عدد نشان‌دهنده‌ی میزان هزینه برای روشن کردن هر چراغ را می‌گوییم. $$1 \leq n \leq 200 \, 000$$ $$1 \leq c_i \leq 1\ 000 \, 000$$ تضمین می‌شود $\sum n$ برای همه‌ی تست‌ها حداکثر $200 \, 000$ باشد. # خروجی عدد نهایی نشان دهنده‌ی کمترین هزینه‌ای که تمام خیابان‌ها روشن شود را چاپ کنید. # مثال‌ها ## ورودی نمونه ۱ ``` 5 5 1 1 1 2 2 3 3 4 7 5 7 5 4 1 1 1 100 7 4 4 4 4 4 4 4 ```` ## خروجی نمونه ۱ ``` 2 3 5 100 12 ```` <details> <summary> **توضیح نمونه ۱** </summary> ---------- اگر چراغ‌های ۱ و ۳ را روشن کنیم. هزینه‌ی $c_1 + c_3 = 1 + 1 = 2$ پرداخت می‌کنیم. همچنین برای هر کدام از محوطه‌ها حداقل یک چراغ مجاورش روشن شده است. ---------- </details> <details> <summary> **توضیح نمونه ۲** </summary> ---------- روشن کردن چراغ اول برای روشن کردن تمام محوطه کافی است و هزینه‌ی روشن کردن آن $c_1 = 3$ است. ---------- </details> <details> <summary> **توضیح نمونه ۳** </summary> ---------- اگر چراغ‌های ۳ و ۵ را روشن کنیم. هزینه‌ی $c_3 + c_5 = 4 + 1 = 5$ پرداخت می‌کنیم. همچنین برای هر کدام از محوطه‌ها حداقل یک چراغ مجاورش روشن شده است. ---------- </details> <details> <summary> **توضیح نمونه ۴** </summary> ---------- در این نمونه دقیقاً یک چراغ وجود دارد. پس باید آن را روشن کنیم تا محوطه روشن شود. ---------- </details> <details> <summary> **توضیح نمونه ۵** </summary> ---------- در این نمونه ۷ چراغ داریم که هزینه‌ی روشن کردن آن‌ها برابر است. برای روشن کردن کل محوطه به روشن کردن حداقل ۳ چراغ نیاز داریم. با روشن کردن ۱، ۴ و ۷ می‌توانیم به این هدف برسیم. پس حداقل هزینه‌ی روشن کردن کل میدان برابر $c_1 + c_4 + c_7 = 4 + 4 + 4 = 12\,$ است. ---------- </details>

+ محدودیت زمان: ۱ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- روی تخته عدد $n$ نوشته شده است. کاپیتان می‌خواهد با انجام تعدادی عملیات این عدد را به ۱ تبدیل کند. او در هر عملیات می‌تواند عدد نوشته شده روی تخته را با یکی از مقسوم‌علیه‌های طبیعی کوچک‌تر از آن عدد جایگزین کند. از آن‌جایی که او می‌خواهد حداکثر استفاده را از تخته گچی بکند، باید طوری این کار را انجام دهد که تعداد عملیات‌ها حداکثر باشد. به چند طریق می‌تواند این عملیات‌ها را انجام دهد به طوری که حداکثر تعداد مرحله را طی کند. دو روش را متقاوت در نظر بگیرید، اگر دنباله‌ی اعدادی که روی تخته نوشته می‌شود متفاوت باشد. # ورودی در تنها سطر ورودی، عدد صحیح و مثبت $n$ داده می‌شود. $$1 \leq n \leq 10^{18}$$ # خروجی باقی‌مانده‌ی پاسخ مسئله بر $10^9 + 7$ را چاپ کنید. # مثال‌ها ## ورودی نمونه ۱ ``` 7 ```` ## خروجی نمونه ۱ ``` 1 ```` <details> <summary> **توضیح نمونه ۱** </summary> ---------- تنها روش ممکن $$ 7 \to 1 $$ است. بنابراین پاسخ ۱ می‌شود. ---------- </details> ## ورودی نمونه ۲ ``` 15 ```` ## خروجی نمونه ۲ ``` 2 ```` <details> <summary> **توضیح نمونه ۲** </summary> ---------- حداکثر طول ممکن ۳ است و ۲ روش $$15 \to 5 \to 1$$ $$15 \to 3 \to 1$$ وجود دارد. بنابراین پاسخ برابر ۲ است. ---------- </details> ## ورودی نمونه ۳ ``` 12 ```` ## خروجی نمونه ۳ ``` 3 ```` <details> <summary> **توضیح نمونه ۳** </summary> ---------- حداکثر طول ممکن ۴ است و ۳ روش $$12 \to 6 \to 3 \to 1$$ $$12 \to 6 \to 2 \to 1$$ $$12 \to 4 \to 2 \to 1$$ وجود دارد. بنابراین پاسخ برابر ۳ است. ---------- </details>

+ محدودیت زمان: ۱ ثانیه + محدودیت حافظه: ۵۱۲ مگابایت ---------- در یک شرکت برنامه‌نویسی، $n$ برنامه‌نویس مشغول به کار هستند. این برنامه‌نویس‌ها با اعداد ۱ تا $n$ شماره‌گذاری می‌شوند. سیستم مدیریتی این شرکت به صورت یک درخت است. یعنی هر برنامه‌نویس به جز برنامه‌نویس شماره‌ی ۱، یک مدیر دارد. مدیر برنامه‌نویس $i$ را با $p_i$ نشان می‌دهیم. در واقع ساختار این شرکت به صورت یک درخت ریشه‌دار است. عید نوروز نزدیک است و این برنامه‌نویس‌ها می‌خواهند از شرکت خارج شوند و برای سفر به شهر کدکاپ بروند. زمانی برنامه‌نویس شماره‌ی $i$ می‌تواند از شرکت خارج شود که $p_i$ هم از سازمان خارج شده باشد. برای هر $k$ از ۱ تا $n$ حساب کنید چند زیرمجموعه $k$ عضوی از برنامه‌نویس‌ها می‌توانند از شرکت خارج شوند. چون ممکن است پاسخ خیلی بزرگ باشد، باقی‌مانده‌ی آن را بر $10^9 + 7$ چاپ کنید. # ورودی در سطر اول ورودی، عدد صحیح و مثبت $n$ آمده که تعداد برنامه‌نویس‌های شرکت را نشان می‌دهد. $$2 \leq n \leq 10 \, 000$$ در سطر دوم ورودی، $n - 1$ عدد صحیح $p_2, p_3, \dots, p_n\,$ می‌آید. $$1 \leq p_i \lt i$$ # خروجی خروجی $n$ سطر دارد و در سطر $k$ام تعداد حالت‌هایی که $k$ نفر شرکت را ترک کنند محاسبه کنید. 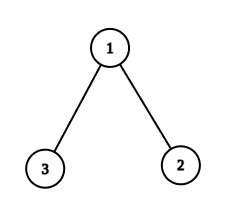# مثال‌ها ## ورودی نمونه ۱ ``` 3 1 1 ``` ## خروجی نمونه ۱ ``` 1 2 1 ``` <details> <summary> **توضیح نمونه ۱** </summary> ----------  + برای حالت $k = 1$ فقط باید یک برنامه‌نویس شرکت را ترک کند و آن فقط $1$ است. (۱ حالت) + برای حالت $k = 2$ فقط باید دو برنامه‌نویس شرکت را ترک کنند و آن‌ها می‌توانند $1, 2$ یا $1, 3$ باشند. (۲ حالت) + برای حالت $k = 3$ فقط باید سه برنامه‌نویس شرکت را ترک کنند و آن‌ها می‌توانند $1, 2, 3$ هستند. 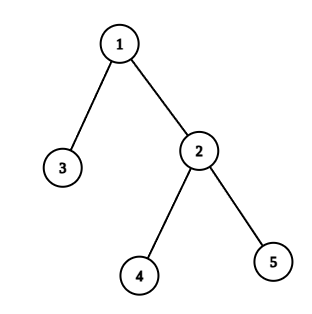(۱ حالت) ---------- </details> ## ورودی نمونه ۲ ``` 5 1 1 2 2 ``` ## خروجی نمونه ۲ ``` 1 2 3 3 1 ``` <details> <summary> **توضیح نمونه ۲** </summary> ----------  مشابه نمونه‌ی قبل مجموعه افرادی که می‌توانند خارج شوند عبارت است از: $$k = 1 \to \{1\}$$ $$k = 2 \to \{1, 2\}, \{1, 3\}$$ $$k = 3 \to \{1, 2, 3\}, \{1, 2, 4\}, \{1, 2, 5\}$$ $$k = 4 \to \{1, 2, 3, 4\}, \{1, 2, 3, 5\}, \{1, 2, 4, 5\}$$ $$k = 5 \to \{1, 2, 3, 4, 5\}$$ ---------- </details>