+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
نقشه کشور کدکاپ از بالا به صورت یک جدول $n \times m$ است. یعنی این کشور، به $nm$ شهر $1 \times 1$ تقسیم میشود.
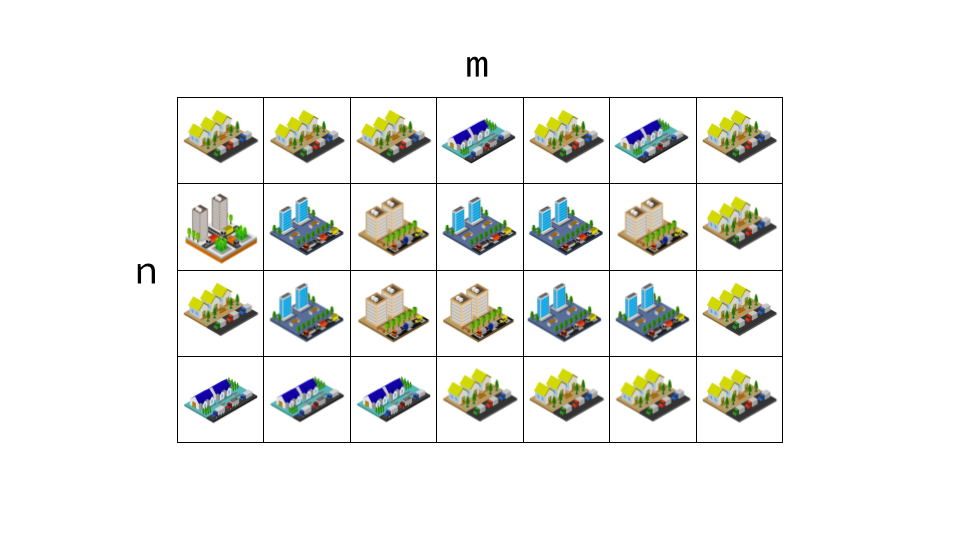
به یک شهر کدکاپ، *مرزی* میگوییم اگر یکی از دیوارهای آن به سمت بیرون کشور باشد. از شما میخواهیم برنامهای بنویسید که با دریافت $n$ و $m$، تعداد شهرهای مرزی کدکاپ را حساب کند.
# ورودی
در سطر اول ورودی، عدد صحیح و مثبت $n$ داده میشود.
$$1\leq n \leq 100$$
در سطر دوم ورودی، عدد صحیح و مثبت $m$ داده میشود.
$$1\leq m \leq 100$$
# خروجی
در تنها سطر خروجی، یک عدد صحیح که نشاندهندهی تعداد شهرهای مرزی کدکاپ را چاپ کنید.
# مثالها
## ورودی نمونه ۱
```
3
4
````
## خروجی نمونه ۱
```
10
````
<details>
<summary>
**توضیح نمونه ۱**
</summary>
در این نمونه، شهرهای کدکاپ، مانند شکل زیر، به صورت یک جدول $3 \times 4$ هستند که ۱۰ شهر مرزی (شهرهایی که به بیرون جدول راه دارند) آن با خانههای ویلایی مشخص شدهاند.
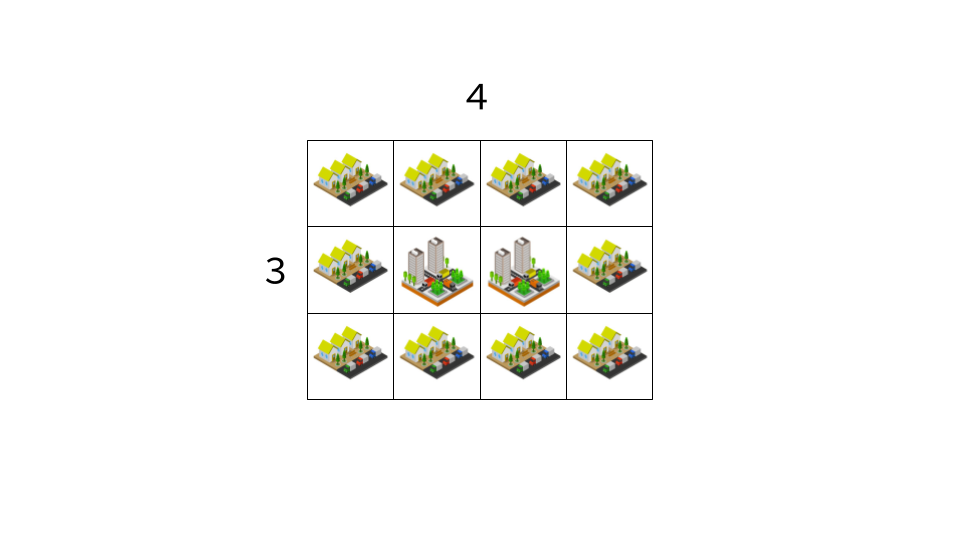
</details>
## ورودی نمونه ۲
```
1
5
````
## خروجی نمونه ۲
```
5
````
<details>
<summary>
**توضیح نمونه ۲**
</summary>
در این نمونه، شهرهای کدکاپ، مانند شکل زیر، به صورت یک جدول $1 \times 5$ هستند که همهی شهرهای آن مرزی (شهرهایی که به بیرون جدول راه دارند) هستند.
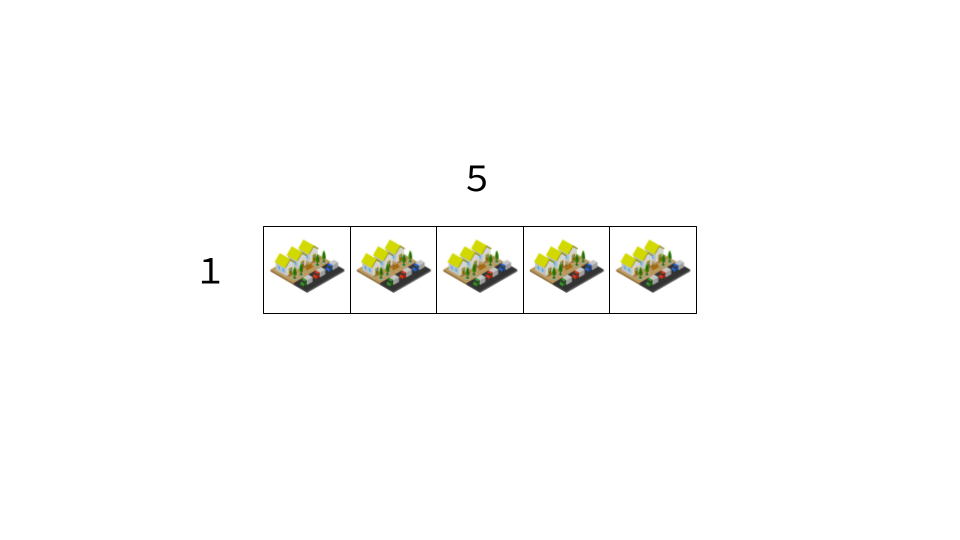
</details>
## ورودی نمونه ۳
```
1
1
````
## خروجی نمونه ۳
```
1
````
<details>
<summary>
**توضیح نمونه ۳**
</summary>
در این نمونه، شهرهای کدکاپ، مانند شکل زیر، به صورت یک جدول $1 \times 1$ هستند و فقط یک شهر دارد و همان شهر هم مرزی (شهری که به بیرون جدول راه دارد) است.
</details>
<details class="red">
<summary>
**اشتباهات متداول**
</summary>
<details class="red">
<summary>
**چک کردن شرایط ورودی مسئله**
</summary>
نیازی نیست چک کنید شرایط گفته شده در ورودی برقرار است یا نه. توضیحات محدودیتها فقط برای آگاهی شما دربارهی تستها و محدودیتهای مسئله است و قطعاً در ورودیهای داده شده به برنامهی شما رعایت میشوند. پس نیازی نیست بنویسید:
```python
if 1 <= n <= 100:
# answer of problem
else:
# print('invalid input')
```
</details>
<details class="red">
<summary>
**ابتدا همهی ورودی را گرفتن و در نهایت همهی خروجی را چاپ کردن**
</summary>
شما میتوانید لابهلای دریافت ورودی، خروجی دهید. پس نیازی نیست ابتدا همهی ورودیها را دریافت کنید و در نهایت همهی خروجیها را چاپ کنید. مخصوصاً برای سوالاتی که باید به چندین سوال پاسخ دهید، میتوانید دو قسمت ورودی و خروجی را کاملاً مستقل در نظر بگیرید و مطمئن باشید تداخلی پیش نمیآید.
</details>
<details class="red">
<summary>
**چاپ کردن موارد اضافه برای دریافت ورودی**
</summary>
لطفاً از چاپ کردن موارد اضافه مثل `please enter a number` برای دریافت ورودی پرهیز کنید. برای مثال در زبان پایتون نباید بنویسید:
```python
input('please enter:')
```
</details>
<details class="red">
<summary>
**چند فایلی کد زدن**
</summary>
برای زبانهایی مثل جاوا نباید در بالای کد شما آدرس پکیج داده شود. برای مثال در بالای کد خود نباید بنویسید:
```java
package ir.quera.contest;
```
</details>
<details class="red">
<summary>
**استفاده از چند `Scanner` برای دریافت ورودی**
</summary>
در زبان جاوا، باید فقط یک شئ از جنس `Scanner` تعریف کنید و همهی ورودیها را با آن دریافت کنید.
</details>
<details class="red">
<summary>
**نحوهی دریافت ورودی و چاپ کردن خروجی**
</summary>
برای آشنایی بیشتر برای نحوهی دریافت ورودی و چاپ کردن خروجی این [لینک](https://quera.org/course/assignments/2693/problems/8774) را مطالعه کنید.
</details>
شهرهای مرزی
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
روی یک میز $2n$ سکه داریم. $n$ سکه در بالای میز با شمارههای ۱ تا $n$ و $n$ سکه در پایین میز با شمارههای ۱ تا $n$ قرار دارند. میدانیم تعدادی (شاید صفر) از سکهها تقلبی، و بقیهی سکهها اصل هستند. سکههای اصل با هم، و سکههای تقلبی باهم، هموزن هستند. همچنین میدانیم وزن سکههای تقلبی **کمتر** از وزن سکههای اصلی است.
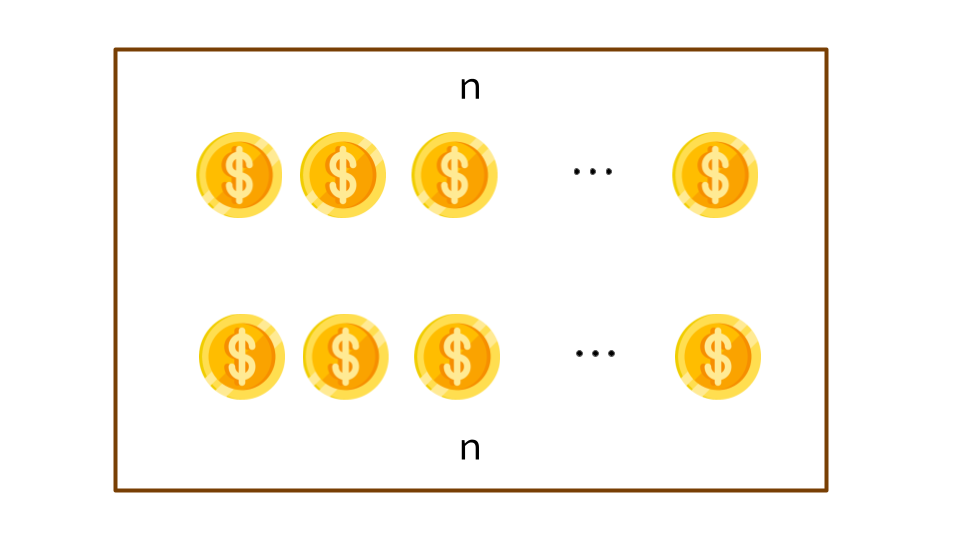
برای هر $i$ و $j$، وزن سکهی $i$ام از طرف بالا میز را با سکهی $j$ام از طرف پایین میز مقایسه کردیم و در صورتی که:
+ وزن سکهی $i$ بالا، کمتر سکهی $j$ پایین بود علامت `<`
+ وزن سکهی $i$ بالا، بیشتر سکهی $j$ پایین بود علامت `>`
+ وزن سکهی $i$ بالا، برابر سکهی $j$ پایین بود علامت `=`
را در سطر $i$ام ستون $j$ام یک جدول $n \times n$ نوشتهایم.
حال میخواهیم از روی این جدول مشخص کنیم کدام سکهها اصل و کدام سکهها تقلبی هستند. ممکن است در جدول داده شده، تناقضی وجود داشته باشد و یا نتوانیم با کمک این دادهها وضعیت را به صورت یکتا مشخص کنیم. از شما میخواهیم برنامهای بنویسید که این سه حالت را شناسایی کرده و نتیجه را اعلام کند.
**برای بهتر متوجه شدن سوال، نمونهها را مطالعه کنید.**
# ورودی
در سطر اول ورودی، عدد صحیح و مثبت $n$ به شما داده میشود.
$$1 \leq n \leq 2 \,,000$$
در $n$ سطر بعدی، در هر سطر $n$ کاراکتر داده میشود که یکی از `<`، `=` یا `>` است. یعنی سکهی $i$ام از $j$ام کوچکتر (`<`)، بزرگتر (`>`) یا مساوی (`=`) است.
# خروجی
اگر اطلاعات داده شده تناقض دارند عبارت `invalid`، در غیراینصورت اگر نمیتوانستیم بهصورت یکتا وضعیت تقلبی یا اصل بودن را شناسایی کنیم عبارت `not unique` و در غیراینصورت در دو سطر، در هر سطر یک رشته از `0` (تقلبی) و `1` (اصل) به طول $n$ چاپ کنید که به ترتیب وضعیت تقلبی یا اصل بودن سکههای بالای و پایین میز را نشان میدهد.
# مثالها
## ورودی نمونه ۱
```
4
<=<<
<=<<
=>==
<=<<
````
## خروجی نمونه ۱
```
0010
1011
````
<details>
<summary>
**توضیح نمونه ۱**
</summary>
اگر وزن ۴ سکهی بالا را با $u_1, u_2, u_3, u_4\,$ و ۴ سکهی پایین را با $d_1, d_2, d_3, d_4 \,$ نشان دهیم. دادههای جدول بالا به صورت زیر هستند:
\[
\begin{array}{cccc}
u_1 \lt d_1 & u_1 = d_2 & u_1 \lt d_3 & u_1 \lt d_4 \\
u_2 \lt d_1 & u_2 = d_2 & u_2 \lt d_3 & u_2 \lt d_4 \\
u_3 = d_1 & u_3 \gt d_2 & u_3 = d_3 & u_3 = d_4 \\
u_4 \lt d_1 & u_4 = d_2 & u_4 \lt d_3 & u_4 \lt d_4 \\
\end{array}
\]
سکههای تقلبی با رنگ نارنجی و سکههای اصل با رنگ زرد در تصویر زیر مشخص شدهاند. این تنها حالت ممکن برای تقلبی یا اصل بودن سکهها است و نتیجه مقایسهها هم همین را نشان میدهد.
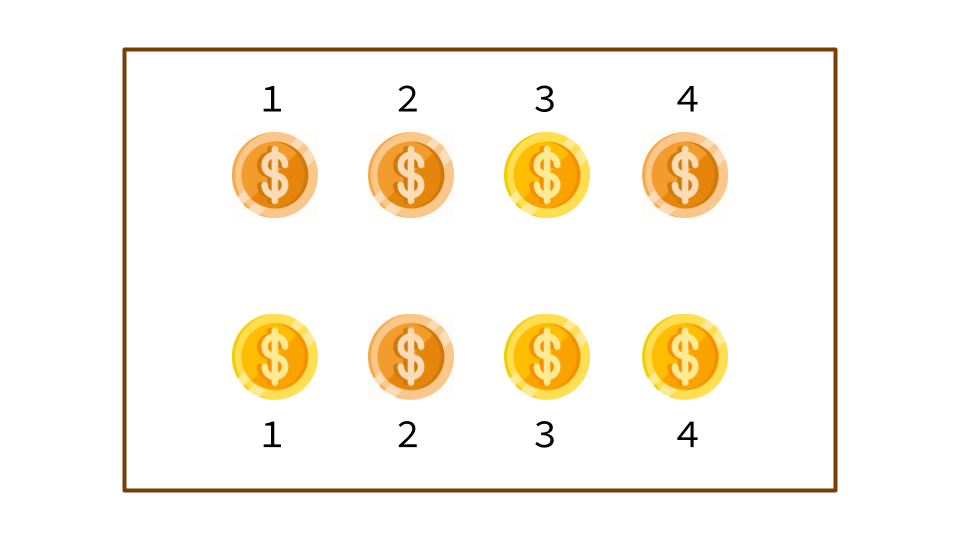
</details>
## ورودی نمونه ۲
```
3
=<<
<=<
<<=
````
## خروجی نمونه ۲
```
invalid
````
<details>
<summary>
**توضیح نمونه ۲**
</summary>
هر دو سکهی ۱ (بالا و پایین)، ۲ و ۳ باهم هموزن هستند. پس میتوانیم وزن آنها را با $w_1$، $w_2$ و $w_3$ نشان دهیم.
میدانیم سکهی ۱ (بالا) از سکهی ۲ (پایین) سبکتر است ($w_1 \lt w_2$). سکهی ۲ (بالا) از سکهی ۱ (پایین) سبکتر است ($w_2 \lt w_1$). و این تناقض است و پاسخ `invalid` میشود.
</details>
## ورودی نمونه ۳
```
1
=
````
## خروجی نمونه ۳
```
not unique
````
<details>
<summary>
**توضیح نمونه ۳**
</summary>
در این حالت دو سکه داریم، سکهی ۱ بالا و سکهی ۱ پایین و میدانیم آنها هموزن هستند. ممکن است هر دو تقلبی و یا هر دو اصل باشند. پس نمیتوان وضعیت آنها را یکتا مشخص کرد و پاسخ `not unique` میشود.
</details>
سکه و وزن
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
یک ساعت شنی داریم که اگر همهی شنهای داخل آن کاملاً در سمت بالا باشد، $M$ دقیقه طول میکشد تا شنها به قسمت پایین منتقل شوند. ما این ساعت شنی را در لحظهی ۰ روی میز قرار دادیم و راس دقیقهی $T$ این ساعت شنی را روی میز بر میداریم. در لحظهی ۰ همهی شنها در قسمت بالایی ساعت قرار دارد.

همچنین $n$ لحظه $t_1, t_2, \dots, t_n\,$ از قبل به ما داده شده و میتوانیم در این لحظهها ساعت شنی را برعکس کنیم، یا هیچ تغییری ندهیم. (در بقیه لحظهها این کار ممکن نیست.) میخواهیم طوری این فرآیند را انجام دهیم که هیچ یک دقیقهی متوالی در این $T$ دقیقه پیش نیاید که ساعت شنی روی میز باشد و همهی شنهایش به قسمت پایین رفته باشد و حرکتی نکند (توجه کنید یک لحظه خالی شدن مهم نیست). از شما میخواهیم برنامهای بنویسید که بررسی کند آیا میتوانیم این کار را انجام دهیم یا خیر؟
برای بهتر متوجه شدن سوال، به توضیح نمونهها توجه کنید.
# ورودی
در سطر اول ورودی، عدد صحیح $t$ آمده که تعداد تستهای یک ورودی را نشان میدهد.
$$1 \leq t \leq 100$$
در سطر اول هر تست سه عدد صحیح $n$، $M$ و $T$ با فاصله از هم داده میشوند.
$$1 \leq n, M \leq 100$$
$$1 \leq T \leq 300$$
در سطر دوم هر تست $n$ عدد صحیح $t_1, t_2, \dots, t_n\,$ داده میشود.
$$0 \lt t_1 \lt t_2 \lt \dots \lt t_n \lt T$$
# خروجی
برای هر تست، در صورتی که این کار شدنی است `YES` و در غیر این صورت `NO` چاپ کنید.
# مثالها
## ورودی نمونه ۱
```
2
2 6 10
3 6
1 10 25
11
````
## خروجی نمونه ۱
```
YES
NO
````
<details>
<summary>
**توضیح نمونه ۱**
</summary>
در تست اول، $M = 6$ دقیقه طول میکشد تا ساعت شنی کاملاً خالی شود. ساعت شنی را در دقیقهی ۰ روی میز قرار میدهیم و در دقیقهی $T = 10$ از روی میز بر میداریم. در دقیقههای $t_1 = 3$ و $t_2 = 6$ میتوانیم ساعت شنی را برعکس کنیم.
اگر در لحظهی $t_2 = 6$ برعکس کنیم هیچ وقت ساعت یک دقیقه متوالی بیحرکت نخواهد بود. چون از دقیقهی ۰ تا ۶ در حال خالی شدن است و درست در همان لحظه، ساعت برعکس میشود و در دقیقهی ۱۰، هنوز به اندازهی ۲ دقیقه شن دارد و هیچوقت ساعت از حرکت نیفتاده است.
در تست اول، $M = 10$ دقیقه طول میکشد تا ساعت شنی کاملاً خالی شود. ساعت شنی را در دقیقهی ۰ روی میز قرار میدهیم و در دقیقهی $T = 25$ از روی میز بر میداریم. در دقیقهی $t_1 = 11$ میتوانیم ساعت شنی را برعکس کنیم.
قبل از رسیدن به اولین زمان ممکن برای تغییر وضعیت ساعت، در بازهی دقیقهی ۱۰ تا ۱۱ ساعت شنی بیحرکت میماند. پس نمیتوانیم به هدفمان برسیم.
</details>
ساعت شنی
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
در یک مهمانی $n$ مهمان حضور دارند. مهمانان این مهمانی کمی عجیبوغریب هستند و هر مهمان تنها با مهمانانی که قد یا وزنشان دقیقاً برابر با اوست حرف میزند! به یک مهمانی **بد** میگوییم اگر مهمانها را بتوان به دو گروه تقسیم کرد، به طوری که هیچ کسی از گروه اول نتواند با هیچ فردی از گروه دوم حرف بزند. میزبان میخواهد تعدادی مهمان جدید دعوت کند که مهمانی دیگر **بد** نباشد.
مثلاً اگر مهمانی فقط شامل دو مهمان یکی با قد ۱۵۰ سانتیمتر و وزن ۷۰ کیلوگرم، و دیگری با قد ۱۸۰ سانتیمتر و وزن ۹۰ کیلوگرم باشد، این دو مهمان نمیتوانند با هم صحبت کنند و بنابراین مهمانی **بد** است. با این حال اگر یک فرد با قد ۱۵۰ سانتیمتر، و وزن ۹۰ کیلوگرم به مهمانی اضافه کنیم، مهمان جدید با هر دو مهمان قبلی میتواند صحبت کند و مهمانی دیگر **بد** نیست.
میزبان آشنایان خیلی زیادی دارد، در نتیجه با هر قد و وزنی که بخواهد میتواند مهمان دعوت کند. میزبان باید حداقل چند میهمان جدید دعوت کند که میهمانی **بد** نباشد؟
# ورودی
در سطر اول ورودی، عدد صحیح و مثبت $n$ که نشان دهندهی تعداد مهمانان اولیه است داده میشود.
$$1 \leq n \leq 300 \, 000$$
در هر کدام از $n$ سطر بعدی، در سطر $i$ام $h_i$ و $w_i$ که نشان دهندهی قد و وزن مهمان $i$ام است داده میشود.
$$1 \leq h_i, w_i \leq 300 \, 000$$
# خروجی
حداقل تعداد مهمان جدیدی که میزبان باید دعوت کند، تا مهمانی **بد** نباشد را چاپ کنید.
# مثالها
## ورودی نمونه ۱
```
2
150 70
180 90
````
## خروجی نمونه ۱
```
1
````
<details>
<summary>
**توضیح نمونه ۱**
</summary>
----------
این مثال در متن سوال توضیح داده شده است.
----------
</details>
## ورودی نمونه ۲
```
3
1 3
1 9
2 4
````
## خروجی نمونه ۲
```
1
````
<details>
<summary>
**توضیح نمونه ۲**
</summary>
----------
اگر مهمانی با قد ۱ و وزن ۴ به مهمانی اضافه شود، دیگر مهمانی بد نیست.
----------
</details>
## ورودی نمونه ۳
```
4
1 3
7 3
2 5
1 5
````
## خروجی نمونه ۳
```
0
````
<details>
<summary>
**توضیح نمونه ۳**
</summary>
----------
مهمانی همین الان هم بد نیست!
----------
</details>
مهمانی بد
+ محدودیت زمان: ۲ ثانیه
+ محدودیت حافظه: ۵۱۲ مگابایت
----------
به یک رشته مثل $s$ یک *جملهی جبری* میگوییم هرگاه فقط از بتوان آن را به دو قسمت مثل $ab$ تقسیم کرد که $a$ یک عدد طبیعی و $b$ رشتهای از حروف کوچک انگلیسی باشد. برای مثال رشتههای `3x` و `115ali` عبارت جبری هستند ولی `1x2y` ،`12` و `xy` عبارت جبری نیستند.
حال به شما یک رشته به طول $n$ مثل $s$ از حروف کوچک انگلیسی (کاراکترهای `a` تا `z`) و ارقام (کاراکترهای `1` تا `9`) داده میشود و از شما $q$ درخواست میشود، در خواستها دو نوع دارند:
+ در درخواست نوع اول، دو عدد $l$ و $r$ که $1 \leq l \leq r \leq n$ است داده میشود و تعداد زیررشتههای متوالی $s_l, s_{l+1}, \dots, s_r$ آن که عبارت جبری هستند را چاپ کنید.
+ در درخواست نوع دوم، عدد $i$ و کاراکتر $c$ به شما داده میشود و از شما میخواهیم $s_i$ را به $c$ تغییر دهید.
منظور از زیررشتهی متوالی یک رشته مثل $s$، رشتهای است که از حذف کردن تعدادی (حتی صفر) کاراکتر از ابتدا و انتهای آن بدست بیاید. برای مثال `ode`، `cup` زیررشتهی متوالی `codecup` است ولی `ccup` و `puc` زیررشتهی متوالی آن نیست.
# ورودی
در سطر اول دو عدد صحیح و مثبت $n$ و $q$ داده میشود.
$$1 \leq n, q \leq 200 \, 000$$
در سطر دوم ورودی رشتهی $s$ شامل $n$ کاراکتر از حروف کوچک و ارقام به طول $n$ داده میشود. در $q$ سطر بعدی در هر سطر یا سه عدد `1` و $l$ و $r$ داده میشود که نشان دهندهی درخواستی از نوع اول است.
$$1 \leq l \leq r \leq n$$
یا دو عدد `2` و $i$ و کاراکتر `c` داده میشود که نشان دهندهی درخواست نوع دوم است.
$$1 \leq i \leq n$$
$$c \in \{a, b, \dots, z, 1, 2, \dots, 9\}$$
# خروجی
در سطرهای جداگانه، به ترتیب پاسخ پاسخ درخواستهای نوع اول را چاپ کنید. تضمین میشود حداقل یک درخواست از نوع اول وجود دارد.
# مثالها
## ورودی نمونه ۱
```
10 6
183xa11u7z
1 1 5
2 2 x
1 1 5
1 5 9
2 9 8
1 1 10
````
## خروجی نمونه ۱
```
6
3
2
6
````
<details>
<summary>
**توضیح نمونه ۱**
</summary>
در درخواست اول تعداد زیررشتههای جبری `183xa` پرسیده شده که برابر ۶ است (`3x`، `3xa`، `83x`، `83xa`، `183x` و `183xa`).
در درخواست دوم رشتهی $s$ به `1x3xa11u7z` تبدیل میشود.
در درخواست سوم تعداد زیررشتههای جبری `1x3xa` پرسیده شده که برابر ۳ است (`1x`، `3x` و `3xa`).
در درخواست چهارم تعداد زیررشتههای جبری `a11u7` پرسیده شده که برابر ۲ است (`1u` و `11u`).
در درخواست پنجم رشتهی $s$ به `1x3xa11u9z` تبدیل میشود.
در درخواست ششم تعداد زیررشتههای جبری `1x3xa11u9z` پرسیده شده که برابر ۶ است (`1x`، `3x`، `3xa`، `1u`، `11u` و `9z`).
</details>
جمله جبری
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
یک جدول $n \times m$ داریم که در خانهی سطر $i$ام، ستون $j$ام آن عدد **حقیقی** $x_{i, j}$ نوشته شده است. باید هر خانهی این جدول مثل $x_{i, j}$ را به $\lfloor x_{i, j} \rfloor$ یا $\lceil x_{i, j} \rceil$ تبدیل کنیم. باید این تغییرات را طوری انجام دهیم به طوری که جمع سطرها و ستونها تغییر نکند.
از شما میخواهیم برنامهای بنویسید که تشخیص دهد انجام این کار شدنی است یا نه و در صورتی که این کار شدنی است، یک روش انجام این کار ارائه دهید.
# ورودی
در سطر اول ورودی، عدد صحیح و مثبت $t$ آمده که تعداد تستها را نشان میدهد.
$$1 \leq t \leq 100$$
در سطر اول هر تست، دو عدد صحیح $n$ و $m$ داده میشود که به ترتیب تعداد سطرها و ستونها جدول را نشان میدهد.
$$1 \leq n, m \leq 100$$
در $n$ سطر بعدی، در هر کدام $m$ عدد حقیقی که با فاصله از هم جدا شدهاند داده میشود. عدد $j$ام در سطر $i$ام همان $x_{i, j}$ است. هر عدد با دقت دقیقاً ۳ رقم بعد از اعشار داده میشود.
$$-1000 \lt x_{i, j} \lt 1000$$
# خروجی
برای هر تست، در سطر اول خروجی، در صورتی که انجام عملیاتها ممکن است، `YES`و در غیر این صورت `NO` را چاپ کنید. برای حالتهایی که انجام عملیاتها ممکن است، یک جدول $n \times m$ چاپ کنید که عدد سطر $i$ام ستون $j$ام آن برابر `0` یا `1` است عدد سطر $i$ام ستون $j$ام به ترتیب نشان دهندهی انتخاب $\lfloor x_{i, j} \rfloor$ یا $\lceil x_{i, j} \rceil$ است.
اگر چند حالت برای رسیدن به جواب وجود دارد، یکی را به دلخواه انتخاب کنید.
# مثالها
## ورودی نمونه ۱
```
3
2 3
3.000 4.000 1.000
5.000 3.000 1.000
3 2
0.500 0.500
0.500 0.500
0.500 1.000
3 3
5.000 3.333 1.667
2.667 0.000 3.333
3.333 2.667 3.000
```
## خروجی نمونه ۱
```
YES
0 0 0
0 0 0
NO
YES
0 0 1
1 1 0
0 1 1
```
<details>
<summary>
**توضیح نمونه ۱**
</summary>
در نمونه اول، چون همهی اعداد جدول صحیح هستند، فرقی ندارد که کدام را $\lfloor . \rfloor$ یا $\lceil . \rceil$ تبدیل کنیم. در هر حال جدول به صورت زیر میشود که جمع سطرها و ستونها ثابت میماند.
\[
\begin{array}{ccc}
3 & 4 & 1 \\
5 & 3 & 1 \\
\end{array}
\]
در نمونهی دوم، هر طوری که $\lfloor . \rfloor$ یا $\lceil . \rceil$ بگذاریم، جمع ستون اول عددی صحیح میشود ولی جمع ستون اول اکنون ۱.۵ است که عددی صحیح نیست. پس جمع این ستون را نمیتوانیم ثابت نگه داریم.
در نمونهی سوم میتوانیم صورت زیر عمل میکنیم و جمع سطرها و ستونها ثابت میماند.
\[
\begin{array}{ccc}
\lfloor 5.000 \rfloor & \lfloor 3.333 \rfloor & \lceil 1.667 \rceil \\
\lceil 2.667 \rceil & \lceil 0.000 \rceil & \lfloor 3.333 \rfloor \\
\lfloor 3.333 \rfloor & \lceil 2.667 \rceil & \lceil 3.000 \rceil \\
\end{array}
\]
</details>