+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
تیم والیبال «کدکاپ» (CodeCup) و تیم والیبال «کوئرا» (Quera) باهم $t$ دَست والیبال بازی کردهاند. میدانیم در دست $i$ام، $n$ امتیاز بین دو تیم رد و بدل شده. هر امتیاز به دقیقاً یکی از دو تیم کدکاپ یا کوئرا رسیده. هر تیمی که زودتر به امتیاز ۲۵ برسد برنده آن دست است.

داور این بازی، حرف اول تیم گیرندهی هر امتیاز را به ترتیب در یک رشتهی $n$ کاراکتری نوشته است. یعنی اگر امتیاز $i$ام را تیم کدکاپ گرفته باشد، کاراکتر $i$ام برابر `C` و اگر امتیاز $i$ام را تیم کوئرا گرفته باشد، کاراکتر $i$ام برابر `Q` است.
میدانیم همهی دستها به درستی داوری شده و به محض برنده شدن یک تیم، آن دست به پایان رسیده. اما این داور فراموش کرده نام تیم برنده را بنویسد. از شما میخواهیم با بررسی کردن این رشتهها، تیم برندهی هر دست را مشخص کنید.
برای بهتر متوجه شدن خواستهی سوال، مثال پایین را مطالعه کنید.
# ورودی
در سطر اول ورودی، عدد صحیح $t$ آمده که تعداد ستها را نشان میدهد.
$$1 \leq t \leq 100$$
در سطر اول هر ست، عدد صحیح $n$ آمده که تعداد امتیازهای رد و بدل شده را نشان میدهد.
$$25 \leq n \leq 49$$
در سطر دوم هر ست، یک رشته از $n$ کاراکتر است که کاراکتر $i$ام برابر `C` است اگر امتیاز را تیم کدکاپ گرفته باشد و `Q` است اگر امتیاز را تیم کوئرا گرفته باشد.
تضمین میشود ورودی درست است و دقیقاً یکی از تیمها در هر ست، برنده شده.
# خروجی
در $t$ سطر برندهی هر ست را به ترتیب چاپ کنید. اگر برنده تیم کدکاپ بود رشتهی `CodeCup` و اگر برنده تیم کوئرا بود `Quera` را چاپ کنید.
**توجه کنید سیستم داوری به بزرگ و کوچک بودن حروف حساس است.**
# مثال
## ورودی نمونه ۱
```
2
44
QQQQCCCQQQQQCCQQQQCQCCCCCCQQQQCCCQQQQQCCCCQQ
25
CCCCCCCCCCCCCCCCCCCCCCCCC
````
## خروجی نمونه ۱
```
Quera
CodeCup
````
<details class="blue">
<summary>
جدول امتیازات دست اول
</summary>
| ردیف | Quera | CodeCup |
|:---|:---:|---:|
| 1 | 1 | 0 |
| 2 | 2 | 0 |
| 3 | 3 | 0 |
| 4 | 4 | 0 |
| 5 | 4 | 1 |
| 6 | 4 | 2 |
| 7 | 4 | 3 |
| 8 | 5 | 3 |
| 9 | 6 | 3 |
| 10 | 7 | 3 |
| 11 | 8 | 3 |
| 12 | 9 | 3 |
| 13 | 9 | 4 |
| 14 | 9 | 5 |
| 15 | 10 | 5 |
| 16 | 11 | 5 |
| 17 | 12 | 5 |
| 18 | 13 | 5 |
| 19 | 13 | 6 |
| 20 | 14 | 6 |
| 21 | 14 | 7 |
| 22 | 14 | 8 |
| 23 | 14 | 9 |
| 24 | 14 | 10 |
| 25 | 14 | 11 |
| 26 | 14 | 12 |
| 27 | 15 | 12 |
| 28 | 16 | 12 |
| 29 | 17 | 12 |
| 30 | 18 | 12 |
| 31 | 18 | 13 |
| 32 | 18 | 14 |
| 33 | 18 | 15 |
| 34 | 19 | 15 |
| 35 | 20 | 15 |
| 36 | 21 | 15 |
| 37 | 22 | 15 |
| 38 | 23 | 15 |
| 39 | 23 | 16 |
| 40 | 23 | 17 |
| 41 | 23 | 18 |
| 42 | 23 | 19 |
| 43 | 24 | 19 |
| 44 | 25 | 19 |
</details>
<details class="blue">
<summary>
جدول امتیازات دست دوم
</summary>
| ردیف | Quera | CodeCup |
|:---|:---:|---:|
| 1 | 0 | 1 |
| 2 | 0 | 2 |
| 3 | 0 | 3 |
| 4 | 0 | 4 |
| 5 | 0 | 5 |
| 6 | 0 | 6 |
| 7 | 0 | 7 |
| 8 | 0 | 8 |
| 9 | 0 | 9 |
| 10 | 0 | 10 |
| 11 | 0 | 11 |
| 12 | 0 | 12 |
| 13 | 0 | 13 |
| 14 | 0 | 14 |
| 15 | 0 | 15 |
| 16 | 0 | 16 |
| 17 | 0 | 17 |
| 18 | 0 | 18 |
| 19 | 0 | 19 |
| 20 | 0 | 20 |
| 21 | 0 | 21 |
| 22 | 0 | 22 |
| 23 | 0 | 23 |
| 24 | 0 | 24 |
| 25 | 0 | 25 |
</details>
برنده والیبال
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------

دنبالهی $\{f_n\}$ برای همهی اعداد طبیعی مثل $n$ ساخته میشود. ابتدا مقدار $f_1 = 2$ درنظر بگیرید. برای $n$های بزرگتر از ۱، مقدار $f_n$ به این صورت بدست میآید:
اگر $n$ عددی زوج باشد:
$$f_n = \lfloor\frac{f_{n-1}}{2}\rfloor \times \lceil\frac{f_{n-1}}{2}\rceil$$
اگر $n$ عددی فرد باشد:
$$ f_n = f_{n-1} - 4$$
منظور از $\lfloor x \rfloor$ (بخوانید کَفِ $x$) بزرگترین عدد صحیح، کوچکتر یا مساوی $x$ است. برای مثال
$\lfloor 3.2 \rfloor = 3$،
$\lfloor -1.3 \rfloor = -2$
و
$\lfloor 2 \rfloor = 2$.
منظور از $\lceil x \rceil$ (بخوانید سَقفِ $x$) کوچکترین عدد صحیح، بزرگتر یا مساوی $x$ است. برای مثال
$\lceil 3.2 \rceil = 4$،
$\lceil -1.3 \rceil = -1$
و
$\lceil 2 \rceil = 2$.
حال از شما $t$ سوال پرسیده میشود. در هر سوال یک عدد طبیعی مثل $n$ داده میشود و از شما مقدار $f_n$ را میخواهند.
# ورودی
در سطر اول ورودی، عدد صحیح و مثبت $t$ آمده که تعداد سوالات را نشان میدهد.
$$1 \leq t \leq 100\,000$$
در $t$ سطر بعدی، در هر سطر، یک عدد صحیح و مثبت مثل $n$ داده میشود.
$$1 \leq n \leq 10^9$$
# خروجی
در $t$ سطر مختلف پاسخ سوالات را به ترتیب چاپ کنید.
# مثالها
## ورودی نمونه ۱
```
5
1
7
2
1403
8
````
## خروجی نمونه ۱
```
2
-3
1
-3
2
````
$f_1 = 2$
$f_2 = \lfloor\frac{f_1}{2}\rfloor \times \lceil\frac{f_1}{2}\rceil = \lfloor\frac{2}{2}\rfloor \times \lceil\frac{2}{2}\rceil = 1 \times 1 = 1$
$f_3 = f_2 - 4 = 1 - 4 = -3$
$f_4 = \lfloor\frac{f_3}{2}\rfloor \times \lceil\frac{f_3}{2}\rceil = \lfloor\frac{-3}{2}\rfloor \times \lceil\frac{-3}{2}\rceil = -2 \times -1 = 2$
$f_5 = f_4 - 4 = 2 - 4 = -2$
$f_6 = \lfloor\frac{f_5}{2}\rfloor \times \lceil\frac{f_5}{2}\rceil = \lfloor\frac{-2}{2}\rfloor \times \lceil\frac{-2}{2}\rceil = -1 \times -1 = 1$
$f_7 = f_6 - 4 = 1 - 4 = -3$
$f_8 = \lfloor\frac{f_7}{2}\rfloor \times \lceil\frac{f_7}{2}\rceil = \lfloor\frac{-3}{2}\rfloor \times \lceil\frac{-3}{2}\rceil = -2 \times -1 = 2$
بازگشت ابدی
+ محدودیت زمان: ۲ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
یک کیک مکعب مستطیلی $a \times b \times c$ موازی محورهای مختصات داریم. در واقع این کیک تمام نقاط $(x, y, z)$ است که $0 \leq x \leq a$، $0 \leq y \leq b$ و $0 \leq z \leq c$ باشد.
داخل این کیک $n$ قطعه شکلات قرار دارد. هر قطعه شکلات یک مکعب مستطیل موازی محورها است. میدانیم که هیچ دو قطعه شکلاتی با هم اشتراک ندارند. هر قطعه شکلات را با شش عدد $x_1, y_1, z_1, x_2, y_2, z_2\,\,\,$ نشان میدهیم و یعنی تمام نقاط $(x, y, z)$ که $x_1 \leq x \leq x_2$، $y_1 \leq y \leq y_2$ و $z_1 \leq z \leq z_2$ از کیک شکلاتی هستند. بقیه فضای کیک را خمیر تشکیل داده است.

خانم کاپکیک میخواهد این کیک را بین $m$ نفر تقسیم کند. او میخواهد کیک را $m - 1$ برش از بالا (موازی صفحهی $yz$) بزند به طوری که $m$ قطعه بدست آمده حجم یکسانی شکلات داشته باشند.
از شما میخواهیم مختصات این برشها را پیدا کنید.
# ورودی
در سطر اول ورودی دو عدد صحیح $n$ و $m$ آمده که به ترتیب تعداد قطعات شکلات و تعداد نفرات را نشان میدهد.
$$1 \leq n \leq 10\,000$$
$$2 \leq m \leq 10\,000$$
در سطر دوم ورودی سه عدد صحیح $a$، $b$ و $c$ آمده که ابعاد کیک را نشان میدهد.
$$1 \leq a, b, c \leq 100$$
در $n$ سطر بعدی، در هر سطر شش عدد صحیح $x_1, y_1, z_1, x_2, y_2, z_2\,\,\,$ داده میشود که مختصات قطعه شکلاتی را نشان میدهد.
$$0 \leq x_1 \lt x_2 \leq a, \quad 0 \leq y_1 \lt y_2 \leq b, \quad 0 \leq z_1 \lt z_2 \leq c$$
تضمین میشود که هیچ دو قطعه شکلاتی با هم اشتراک ندارند.
# خروجی
خروجی $m - 1$ خط دارد و در خط $i$ام عدد اعشاری $X_i$ که نشان دهندهی برشی است که باید بزنیم. شما باید برشها را به ترتیب چاپ کنید یعنی:
$$0 \lt X_1 \lt X_2 \lt \dots \lt X_{m-1} \lt a$$
زمانی پاسخ شما پذیرفته میشود که اختلاف حجم شکلاتی که به هر کس میرسد با مقدار دقیق آن حداکثر ۰.۰۰۱ باشد.
# مثال
## ورودی نمونه ۱
```
2 3
3 4 5
0 0 0 1 1 1
2 2 2 3 4 5
```
## خروجی نمونه ۱
```
2.222222222217
2.611111111103
```
عدالت شکلاتی
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
در کشور کدکاپ $n$ شهر وجود دارد. شهرهای کدکاپ با اعداد $1$ تا $n$ شمارهگذاری شدهاند. بین شهرهای کدکاپ تعدادی جاده قرار دارد. میدانیم هر جاده دو طرفه است و دقیقاً دو شهر مختلف را به هم متصل میکند. در واقع نقشه کشور کدکاپ، بهصورت یک گراف ساده است.
به سه شهر مختلف مثل $u$، $v$ و $w$ یک *مثلث* میگوییم، هرگاه بین $uv$، $vw$ و $uw$ یک جاده وجود داشته باشد.
نقشهی کشور کدکاپ گم شده اما تعداد شهرهای آن یعنی $n$ را میدانیم. همچنین برای $m$ جفت از شهرها مثل $a_i$ و $b_i$ میدانیم شهر $a_i$ و شهر $b_i$ باهم در حداقل یک مثلث آمدهاند. یعنی شهر دیگری مثل $c_i$ وجود دارد که این سهشهر باهم یک مثلث تشکیل میدهند. توجه کنید که مقدار $c_i$ را نداریم.
همچنین برای $k$ جفت از شهرها مثل $a_i$ و $b_i$ میدانیم در هیچ مثلثی نیامدهاند. یعنی هیچ شهری مثل $c_i$ وجود ندارد که با آنها تشکیل مثلث بدهد.
حال از شما میخواهیم باتوجه به این اطلاعات بررسی کنید نقشهی قابل قبولی برای کشور کدکاپ وجود دارد یا نه. همچنین در صورت وجود چنین کشوری، یک مثال از آن را ارائه کنید.
# ورودی
در سطر اول ورودی، عدد صحیح $t$ آمده که تعداد تستها را نشان میدهد.
$$1 \leq t \leq 1000$$
در سطر اول هر تست سه عدد $n$، $m$ و $k$ آمده است که به ترتیب تعداد شهرهای کدکاپ قدیم، تعداد جفت شهرهایی که در حداقل یک مثلث آمدهاند و تعداد جفت شهرهایی که در هیچ مثلثی نیامدهاند.
$$1 \leq n \leq 1000, \quad 0 \leq m + k \leq \frac{n(n - 1)}{2}$$
در $m+k$ سطر بعدی، در هر سطر دو شهر $u$ و $v$ آمده که $m$ جفت اول در حداقل یک مثلث آمدهاند و $k$ جفت آخر در هیچ مثلثی نیامدهاند.
$$1 \leq u \neq v \leq n$$
تضمین میشود که هر جفت شهر حداکثر یکبار بیاید. همچنین مجموع $n$ برای همهی تستها حداکثر ۱۰۰۰ باشد.
# خروجی
با عبارت `YES` و `NO` بگویید چنین گرافی وجود دارد یا نه. اگر جواب `YES` بود یک نقشه با شرایط گفته شده چاپ کنید.
برای چاپ کردن نقشه، در سطر بعد از `YES` عدد $e$ را چاپ کنید که تعداد جادههای موجود را نشان میدهد. سپس در $e$ سطر بعدی در هر سطر دو عدد صحیح مثل $u$ و $v$ با یک فاصله از هم چاپ کنید که وجود یک جاده بین $u$ و $v$ را نشان میدهد.
توجه کنید باید هر جاده را حداکثر یکبار چاپ کنید و هیچ جادهای ابتدا و انتهای یکسانی نداشته باشند. اگر چند جواب برای مسئله وجود دارد، یکی را به دلخواه چاپ کنید.
# مثالها
## ورودی نمونه ۱
```
4
3 0 0
3 1 0
2 1
3 2 0
1 2
3 1
3 1 2
2 1
3 1
2 3
```
## خروجی نمونه ۱
```
YES
2
2 1
1 3
YES
3
1 2
3 1
3 2
YES
3
1 2
1 3
2 3
NO
```
مثلث گمشده
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
تصویر زیر، نمای کوه کدکاپ است. میدانیم ارتفاع این کوه از هر دو طرف تا قله همواره صعودی است. توجه کنید ممکن است در بازهای ارتفاع ثابت بماند اما هیچوقت در مسیر قله، ارتفاع کاهش نمییابد.
زمینشناسان $n$ نقطه در کوه کدکاپ را انتخاب کرده و ارتفاع کوه را در آن نقاط را اندازه گیری کردهاند. ارتفاع این نقاط را به ترتیب از چپ به راست با $h_1, h_2, \dots, h_n\,$ مشخص میکنیم. با این حال اندازهگیری زمینشناسان خطا دارد و ارتفاع واقعی کوه در این $n$ نقطه برابر با اعداد اندازهگیری شده نیست. ارتفاع واقعی کوه را در این $n$ نقطه با $H_1, H_2, \dots, H_n\,$ نشان میدهیم.

بنابراین با توجه به ویژگی کوه کدکاپ میدانیم دنبالهی $H$ در ابتدا صعودی و سپس نزولی است. یعنی عدد صحیحی مثل $i$ که $1 \leq i \leq n$ وجود دارد به طوری که $H_1, H_2, \dots, H_i\,$ تشکیل یک دنبالهی صعودی و دنبالهی $H_{i+1}, H_{i+2}, \dots, H_n\,$ تشکیل یک دنبالهی نزولی بدهد.
به یک دنباله مثل $a_1, a_2, \dots, a_n\,$ صعودی میگوییم هرگاه $a_1 \leq a_2 \leq \dots \leq a_n\,$ باشد. به یک دنباله مثل $a_1, a_2, \dots, a_n\,$ نزولی میگوییم هرگاه $a_1 \geq a_2 \geq \dots \geq a_n\,$ باشد.
میگوییم خطای اندازهگیری $k$ است اگر هر کدام از $h_i$ها حداکثر $k$ واحد با $H_i$ اختلاف داشته باشد. ($|h_i-H_i|\leq k\,$)
به شما دنبالهی $h_1, h_2, \dots, h_n\,$ داده میشود. از شما میخواهیم کمینه خطای ممکن برای این دادهها را حساب کنید. یعنی کوچکترین $k$ی **صحیحی** را پیدا کنید که دنبالهای مثل $H$ وجود داشته باشد که هر عضوش با $h$ حداکثر $k$ واحد اختلاف داشته باشد و در ابتدا صعود و سپس نزولی باشد.
# ورودی
در سطر اول ورودی، عدد صحیح $t$ آمده که تعداد تستها را نشان میدهد.
$$1 \leq t \leq 200\,000$$
در سطر اول هر تست، عدد صحیح و مثبت $n$ آمده که تعداد اعداد آرایه را نشان میدهد.
$$1 \leq n \leq 200\,000$$
در سطر دوم هر تست، $n$ عدد $h_1, h_2, \dots, h_n\,$ با فاصله از هم آمده است.
$$1 \leq h_i \leq 10^9$$
توجه کنید که با وجود این که $h_i$ عددی است، $H_i$ ممکن است هر عددی شامل اعداد منفی یا بزرگتر از $10^9$ باشد.
تضمین میشود مجموع $n$ها برای همهی تستها حداکثر ۲۰۰،۰۰۰ باشد.
# خروجی
در $t$ سطر کمینه خطای ممکن برای هر تست را به ترتیب چاپ کنید.
# مثال
## ورودی نمونه ۱
```
2
5
10 20 30 20 10
7
1 4 1 3 2 1 3
```
## خروجی نمونه ۱
```
0
1
```
اندازهگیری کوه
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
سر چنگک آقا و خانم پیت کند شده و آنها میخواهند سر آن را تعویض کند.

برای تعویض سر چنگک، آقا و خانم پیت به سراغ یک درخت $n$ راسی میروند. برای ساخت سر یک چنگک آنها باید **یال**های یک زیرگراف $3x$ یالی خاص را از درخت حذف کنند. این زیرگراف خاص از $3$ مسیر $x$ یالی تشکیل شده است که راس اولشان با هم مشترک است. این گراف برای حالت $x=2$ در شکل نمایش داده شده است.
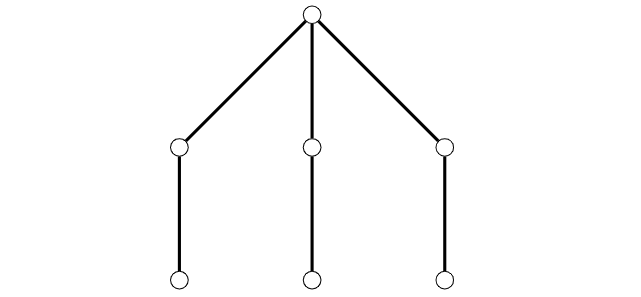
آقا و خانم پیت با استفاده از این درخت حداکثر چند سر چنگک میتوانند بسازند؟ توجه کنید که آقا و خانم پیت راسهای درخت را هیچگاه حذف نمیکنند. آنها تنها یک زیرگراف مشابه شکل پیدا میکنند و **یال**های آن را از درخت حذف میکنند. بنابراین دو چنگک میتوانند در راس با هم اشتراک داشته باشند.
# ورودی
در سطر اول ورودی، ابتدا عدد طبیعی $n$ و سپس $x$ داده میشود.
$$1\leq n \leq 300\,000$$
$$1\leq x \leq 100\,000$$
در سطر دوم ورودی، $n-1$ عدد $a_2, a_3, a_4, ,..., a_n$ داده میشود.
که عدد $a_i$ نشان دهندهی این است که راس $i$ به راس $a_i$ در درخت متصل است.
$$1\leq a_i \leq n$$
تضمین میشود گراف حاصل یک درخت است.
# خروجی
در تنها سطر خروجی، یک عدد صحیح که نشان دهندهی حداکثر تعداد چنگکهایی است که آقا و خانم پیت میتوانند با استفاده از درخت بسازند را چاپ کنید.
# مثالها
## ورودی نمونه ۱
```
5 1
1 1 3 3
````
## خروجی نمونه ۱
```
1
````
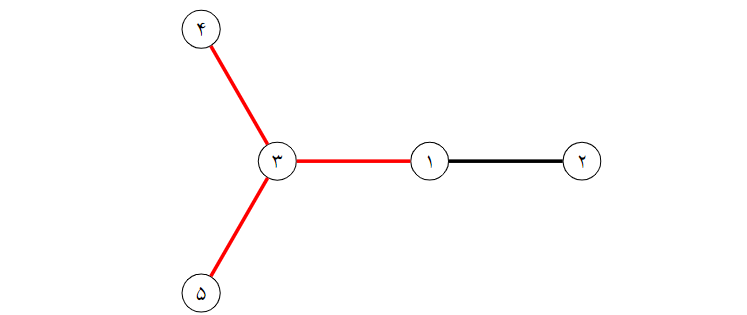
یالهایی که آقا و خانم پیت برای ساخت سر چنگک اولشان باید حذف کنند با رنگ قرمز مشخص شده است.
## ورودی نمونه ۲
```
7 1
1 1 3 3 2 2
````
## خروجی نمونه ۲
```
2
````
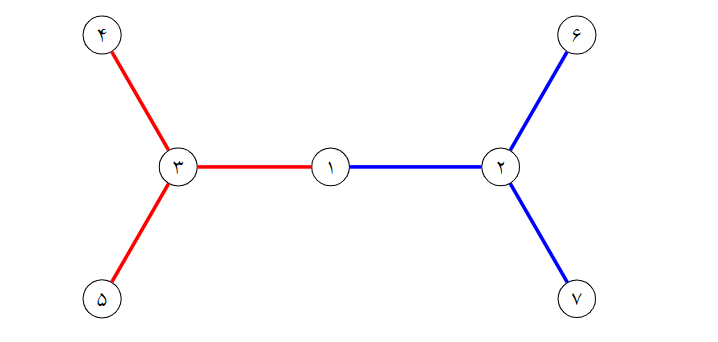
یالهایی که آقاو خانم پیت برای سر چنگک اول حذف میکنند با رنگ قرمز و یالهای که برای سر چنگک دوم حذف میکنند با رنگ آبی مشخص شدهاست.
## ورودی نمونه ۳
```
8 1
1 1 1 1 1 1 1
````
## خروجی نمونه ۳
```
2
````
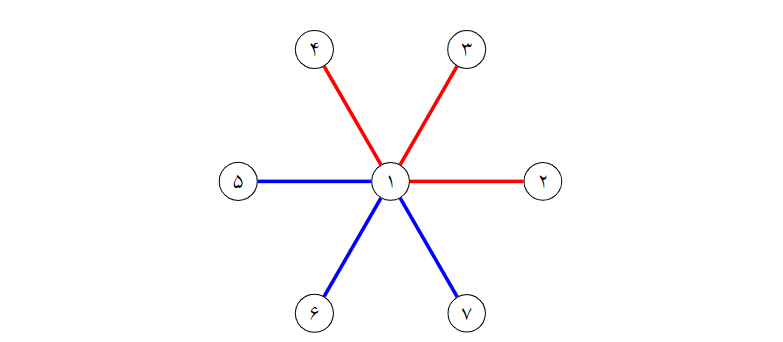
یالهایی که آقا و خانم پیت برای سر چنگک اول حذف میکنند با رنگ قرمز و یالهایی که برای سر چنگک دوم حذف میکنند با رنگ آبی مشخص شدهاست.
## ورودی نمونه ۴
```
12 2
1 2 3 4 4 5 6 1 1 9 10
````
## خروجی نمونه ۴
```
1
````
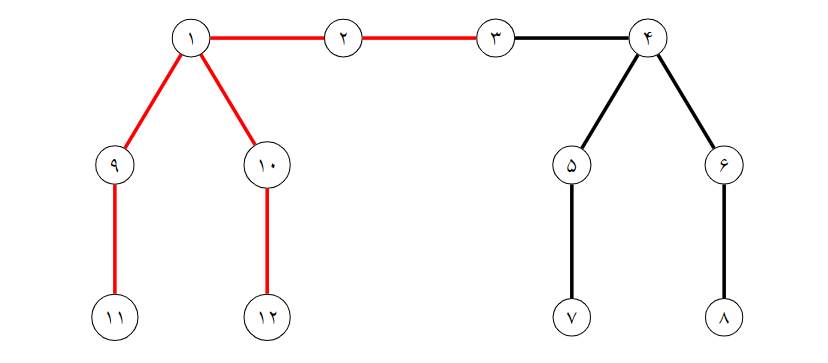
یالهایی که آقا و خانم پیت برای ساخت سر چنگکشان استفاده میکنند با رنگ قرمز مشخص شده است.