+ محدودیت زمان: ۱ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- یک قورباغه در چاهی به عمق $h$ متر گیر کرده است. او روزها تلاش می‌کند و $a$ متر از دیوار بالا می‌رود و شب‌ها که می‌خوابد $b$ متر به سمت پایین سر می‌خورد.  اولین لحظه‌ای که ارتفاع او از $h$ بیشتر یا مساوی شود، از چاه خارج می‌شود. از شما می‌خواهیم بررسی کنید حداقل چند روز طول می‌کشد تا قورباغه از چاه خارج شود. برای بهتر متوجه شدن خواسته‌ی سوال به قسمت مثال‌ها مراجعه کنید. # ورودی در سطر اول ورودی، عدد صحیح و مثبت $t$ آمده که تعداد تست‌ها را نشان می‌دهد. $$1 \leq t \leq 100$$ در $t$ سطر بعدی در هر سطر سه عدد $a$، $b$ و $h$ آمده است. $$0 \leq b \lt a \leq h \leq 100$$ # خروجی در $t$ سطر به ترتیب شماره‌ی روزی که قورباغه از چاه خارج شده را چاپ کنید. # مثال‌ها ## ورودی نمونه ۱ ``` 3 3 1 30 3 1 31 10 5 10 ```` ## خروجی نمونه ۱ ``` 15 15 1 ```` در تست اول و دوم حرکت قورباغه به صورت زیر است: + روز ۱ تا ارتفاع $3 + 0 = 3$ بالا می‌رود. + شب ۱ به ارتفاع $3 - 1 = 2$ سر می‌خورد. + روز ۲ تا ارتفاع $2 + 3 = 5$ بالا می‌رود. + شب ۲ به ارتفاع $5 - 1 = 4$ سر می‌خورد. + روز ۳ تا ارتفاع $4 + 3 = 7$ بالا می‌رود. + شب ۳ به ارتفاع $7 - 1 = 6$ سر می‌خورد. + ... + روز ۱۴ تا ارتفاع $26 + 3 = 29$ بالا می‌رود. + شب ۱۴ به ارتفاع $29 - 1 = 28$ سر می‌خورد. + روز ۱۵ تا ارتفاع $28 + 3 = 31$ بالا می‌رود و نجات پیدا می‌کند. در تست سوم در روز اول قورباغه تا ارتفاع $10 + 0 = 10$ بالا می‌رود و از چاه خارج می‌شود. <details class="red"> <summary> **اشتباهات متداول** </summary> <details class="red"> <summary> **چک کردن شرایط ورودی مسئله** </summary> نیازی نیست چک کنید شرایط گفته شده در ورودی برقرار است یا نه. توضیحات محدودیت‌ها فقط برای آگاهی شما درباره‌ی تست‌ها و محدودیت‌های مسئله است و قطعاً در ورودی‌های داده شده به برنامه‌ی شما رعایت می‌شوند. پس نیازی نیست بنویسید: ```python if 1 <= n <= 100: # answer of problem else: # print('invalid input') ``` </details> <details class="red"> <summary> **ابتدا همه‌ی ورودی را گرفتن و در نهایت همه‌ی خروجی را چاپ کردن** </summary> شما می‌توانید لابه‌لای دریافت ورودی، خروجی دهید. پس نیازی نیست ابتدا همه‌ی ورودی‌ها را دریافت کنید و در نهایت همه‌ی خروجی‌ها را چاپ کنید. مخصوصاً برای سوالاتی که باید به چندین سوال پاسخ دهید، می‌توانید دو قسمت ورودی و خروجی را کاملاً مستقل در نظر بگیرید و مطمئن باشید تداخلی پیش نمی‌آید. </details> <details class="red"> <summary> **چاپ کردن موارد اضافه برای دریافت ورودی** </summary> لطفاً از چاپ کردن موارد اضافه مثل `please enter a number` برای دریافت ورودی پرهیز کنید. برای مثال در زبان پایتون نباید بنویسید: ```python input('please enter:') ``` </details> <details class="red"> <summary> **چند فایلی کد زدن** </summary> برای زبان‌هایی مثل جاوا نباید در بالای کد شما آدرس پکیج داده شود. برای مثال در بالای کد خود نباید بنویسید: ```java package ir.quera.contest; ``` </details> <details class="red"> <summary> **استفاده از چند `Scanner` برای دریافت ورودی** </summary> در زبان جاوا، باید فقط یک شئ از جنس `Scanner` تعریف کنید و همه‌ی ورودی‌ها را با آن دریافت کنید. </details> <details class="red"> <summary> **نحوه‌ی دریافت ورودی و چاپ کردن خروجی** </summary> برای آشنایی بیشتر برای نحوه‌ی دریافت ورودی و چاپ کردن خروجی این [لینک](https://quera.org/course/assignments/2693/problems/8774) را مطالعه کنید. </details>

+ محدودیت زمان: ۱ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- کارکنان کوئرا می‌خواهند به یک سینما که گنجایش $k$ نفر را دارد، بروند. مشکل این است که برای هر کارمند کوئرا که به سینما برود، او باید حتماً به همراه تمام دوستانش برود. اگر کارمند $i$ام کوئرا $a_i$ دوست داشته باشد (به جز خودش)، حداکثر چند نفر از اعضای کوئرا می‌توانند همزمان به سینما بروند؟  # ورودی در سطر اول ورودی، دو عدد طبیعی $n$ و $k$ که به ترتیب تعداد کارکنان کوئرا و گنجایش سینما را نشان می‌دهند، داده می‌شود.$$1\leq n \leq 100\,000$$ $$1\leq k \leq 10^9$$ در سطر بعدی $n$ عدد صحیح داده می‌شود که عدد $i$ام تعداد دوستان کارمند $i$ام کوئرا است. $$0 \leq a_i \leq 10^9$$ # خروجی در تنها سطر خروجی حداکثر تعداد کارمندان کوئرا که می‌توانند با هم به سینما بروند را چاپ کنید. # مثال‌ها ## ورودی نمونه ۱ ``` 5 10 4 3 0 2 1 ```` ## خروجی نمونه ۱ ``` 4 ```` اگر همه‌ی ۵ کارمند کوئرا با دوستانشان بیایند، ۱۵ نفر می‌شوند ولی ظرفیت سینما ۱۰ نفر است. اما اگر کارمند ۱ و دوستانش نیایند دقیقاً ۱۰ نفر می‌شوند. بنابراین پاسخ مسئله ۴‌ یعنی تعداد کارمندانی که به سینما می‌آیند، است.

+ محدودیت زمان: ۱ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- مدتی است که امین خیلی پرمشغله شده است. به همین دلیل کار همه پیش او گیر است و از امین درخواست کرده‌اند که **شماره‌تلفن** خودش را به آن‌ها بدهد.  امین نمی‌خواهد کار آن‌ها را راحت کند تا با تماس‌هایشان کار او را بیشتر کنند. به همین دلیل تصمیم گرفته‌است شماره‌تلفن خود را به بخش های **به طول ۲ یا ۳** ، تکه تکه (افراز) کند و هر تکه را به یک نفر بدهد. هر تکه باید با یک عدد **ناصفر** شروع شود. به ازای هر شماره‌ی امین به او بگویید آیا این‌کار امکان پذیر است یا نه و در صورت امکان پذیر بودن یک روش ارائه کنید. برای بهتر متوجه شدن خواسته‌ی سوال به مثال‌ها مراجعه کنید. # ورودی در سطر اول ورودی، عدد طبیعی $q$ داده می‌شود که نشانگر تعداد شماره‌تلفن‌های امین است. $$1\leq q \leq 3000$$ در $2q$ سطر بعدی اطلاعات شماره‌تلفن‌ها آمده است. به این شکل که در سطر $ 2i - 1$ عدد $y_i$ به عنوان طول شماره تلفن و در سطر بعدی آن، رشته $x_i$ که از ارقام `0` تا `9` تشکیل شده و بیانگر شماره‌تلفن $i$ام امین است داده می‌شود. $$0 \leq y_i \leq 100\,000$$ مجموع طول تمام شماره تلفن‌ها حداکثر $100\,000$ است. # خروجی پاسخ شما باید شامل $q$ خط باشد. در خط $i$ام باید ‍‍‍`YES` چاپ کنید، اگر امین می‌تواند شماره‌تلفن مورد نظر را به تکه‌های درستی افراز کند. در این حالت باید در سطر بعدی عدد $k$ که نشان دهنده‌ی تعداد تکه‌ها است را چاپ کنید و در $k$ سطر بعدی در هر سطر تکه‌های شماره‌ی تلفن را به ترتیب چاپ کنید. اگر چند روش صحیح برای تکه کردن وجود دارد یکی را به دلخواه چاپ کنید. و در صورتی که هیچ راهی وجود ندارد که امین بتواند شماره‌تلفن مورد نظر را به تکه‌های درستی افراز کند `NO` چاپ کنید. # مثال‌ها ## ورودی نمونه ۱ ``` 7 5 12345 2 83 1 4 5 09999 4 1023 4 1203 5 11203 ```` ## خروجی نمونه ۱ ``` YES 2 12 345 YES 1 83 NO NO YES 2 10 23 NO YES 2 11 203 ```` + شماره‌ی اول امین `12345` است و می‌توانیم آن را به دو قسمت `12` و `345` تقسیم کنیم. (توجه کنید تقسیم ‍`12` و `345` هم درست است.) + شماره‌ی دوم امین `83` است و خودش یک قسمت است. (توجه کنید تقسیم `8` و `3` درست نیست چون اندازه‌ی قسمت‌ها باید ۲ یا ۳ باشد.) + شماره‌ی سوم امین `4` است و یک شماره‌ی یک رقمی است پس نمی‌توانیم آن را به بخش‌های ۲ یا ۳ رقمی تقسیم کنیم. + شماره‌ی چهارم امین `09999` است و هر طوری که قسمت کنیم بخش اول با صفر شروع می‌شود پس این کار شدنی نیست. + شماره‌ی پنجم امین `1023` است و ‌می‌توانیم آن را به دو قسمت `10` و `23` تقسیم کنیم. + شماره‌ی ششم امین `1203` است و نمی‌توانیم آن را به دو قسمت ۲ یا ۳ رقمی تقسیم کنیم که هیچ بخشی از آن با صفر شروع نشود. + شماره‌ی هفتم امین `11203` است و می‌توانیم آن را به دو قسمت `11` و `203` تقسیم کنیم. (توجه کنید تقسیم `112` و `03` درست نیست چون بخش دوم با صفر شروع می‌شود.)

+ محدودیت زمان: ۱ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- یک مهره‌ی اسب در خانه‌ی مرکزی یک جدول که از هر طرف نامتناهی است، قرار دارد. این مهره یک خانه را به عنوان مقصد خود انتخاب کرده است و می‌خواهد به سریع‌ترین روش ممکن به آن خانه‌ برسد. شما باید این کمترین تعداد حرکت ممکن را پیدا کنید. به طور دقیق‌تر، در ابتدا اسب در خانه‌ی $(0,0)$ جدول قرار دارد شما باید حداقل تعداد حرکت مورد نیاز برای رفتن اسب به خانه‌ی $(x,y)$ را پیدا کنید. مهره‌ی اسب در هر حرکت می‌تواند در یکی از جهت‌های عمودی یا افقی دو خانه به پیش برود و در جهت دیگر یک خانه به جلو برود. این هشت خانه‌ در شکل زیر با رنگ قرمز مشخص شده‌اند.  # ورودی در سطر اول ورودی، عدد طبیعی $t$ داده می‌شود. $$1\leq t \leq 3000$$ در سطر $i$ام از $t$ سطر بعدی، دو عدد $x_i$ و $y_i$ آمده است. $$0\leq x_i,y_i \leq 10^9$$ # خروجی پاسخ شما باید شامل $t$ خط باشد. در خط $i$ام باید حداقل حرکت مورد نیاز اسب برای رسیدن به $(x_i,y_i)$ با شروع از $(0,0)$ را چاپ کنید. # مثال‌ها ## ورودی نمونه ۱ ``` 6 1 1 2 1 2 2 3 3 3 1 2000 0 ```` ## خروجی نمونه ۱ ``` 2 1 4 2 2 1000 ````  + مسیر رسیدن اسب به خانه‌ی $(1,1)$ را می‌توانید در شکل زیر با توجه به اعداد صورتی پیدا کنید. + مسیر رسیدن اسب به خانه‌ی $(2,1)$ را می‌توانید در شکل زیر با توجه به عدد قهوه‌ای پیدا کنید. + مسیر رسیدن اسب به خانه‌ی $(2,2)$ را می‌توانید در شکل زیر با توجه به اعداد سیاه پیدا کنید. + مسیر رسیدن اسب به خانه‌ی $(3,3)$ را می‌توانید در شکل زیر با توجه به اعداد بنفش پیدا کنید. + مسیر رسیدن اسب به خانه‌ی $(3,1)$ را می‌توانید در شکل زیر با توجه به اعداد صورتی آبی پیدا کنید.

+ محدودیت زمان: ۲ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- در یک کشور $n$ شهر وجود دارد. شهرها با اعداد ۱ تا $n$ شماره‌گذاری شده‌اند. بین این شهرها $m$ جاده دو طرفه وجود دارد. هر جاده دقیقاً دو شهر را بهم وصل می‌کند. برای هر جاده می‌دانیم محدودیت ارتفاع ورود عبور کامیون‌ها چقدر است. اگر این محدودیت عدد $h_i$ باشد یعنی کامیون‌های با ارتفاع بیشتر از $h_i$ اجازه‌ی ورود به این جاده را ندارند.  از شما $q$ راننده کامیون سوال می‌پرسند. راننده‌ی $j$ام می‌خواهد از شهر شماره‌ی $u_j$ به شهر شماره‌ی $v_j$ برود و ارتفاع بار کامیون آن $h_j$ است، آیا مسیری (نه لزوماً کوتاه‌ترین) برای این سفر وجود دارد یا نه؟ # ورودی در سطر اول ورودی، دو عدد صحیح و مثبت $n$ و $m$ آمده که تعداد شهرها و جاده‌ها را نشان می‌دهد. $$1 \leq n, m \leq 1000 \, 000$$ در $m$ سطر بعدی، در سطر $i$ام سه عدد $u_i$ و $v_i$ و $h_i$ می‌آید که نشان دهنده‌ی وجود یک جاده بین شهر $u_i$ و $v_i$ با محدودیت ارتفاع حداکثر $h_i$ است. $$1 \leq u_i, v_i \leq n, \quad \quad 1 \leq h_i \leq 10^9$$ در سطر بعدی عدد صحیح و مثبت $q$ آمده که تعداد راننده کامیون‌ها را نشان می‌دهد. $$1 \leq q \leq 1000\,000$$ در $q$ سطر بعدی، در سطر $j$ام سه عدد $u_j$ و $v_j$ و $h_j$ می‌آید که یعنی این راننده می‌خواهد از شهر شماره‌ی $u_j$ به شهر شماره‌ی $v_j$ برود و ارتفاع بار کامیون آن $h_j$ است. $$1 \leq u_j, v_j \leq n, \quad \quad 1 \leq h_j \leq 10^9$$ # خروجی در $q$ سطر، در صورتی که انجام این سفر برای راننده شدنی است `YES` و در غیر این صورت `NO` چاپ کنید. 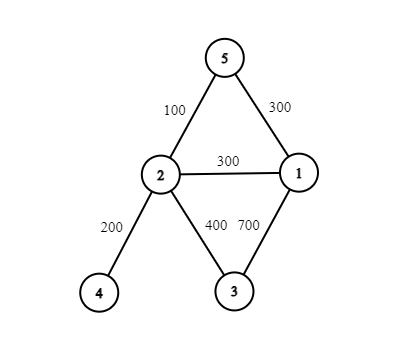# مثال‌ها ## ورودی نمونه ۱ ``` 5 6 1 2 300 1 3 700 2 4 200 2 5 100 1 5 300 2 3 400 4 3 5 300 3 5 600 1 3 200 2 4 500 ```` ## خروجی نمونه ۱ ``` YES NO YES NO ````  شکل بالا وضعیت شهرها و جاده‌ها را نشان می‌دهد. + کامیون اول می‌خواهد از شهر ۳ به شهر ۵ با ارتفاع بار ۳۰۰ برود. اگر از شهر ۳ به شهر ۱ و از شهر ۱ به شهر ۵ برود. هیچ مشکلی با پل‌های عابر میان راه نمی‌خورد. بنابراین پاسخ `YES` است. + کامیون دوم می‌خواهد از شهر ۳ به شهر ۵ با ارتفاع بار ۶۰۰ برود اما هیچ جاده‌ای به شهر ۵ وجود ندارد که چنین ارتفاعی را مجاز کند. بنابراین پاسخ `NO` است. + کامیون سوم می‌خواهد از شهر ۱ به شهر ۳ با ارتفاع بار ۲۰۰ برود. اگر از جاده‌ی مستقیم استفاده کند این کار شدنی است. پس پاسخ `YES` است. + کامیون چهارم می‌خواهد از شهر ۲ به شهر ۴ با ارتفاع بار ۵۰۰ برود اما هیچ جاده‌ای به شهر ۴ وجود ندارد که چنین ارتفاع باری را مجاز کند. بنابراین پاسخ `NO` است.

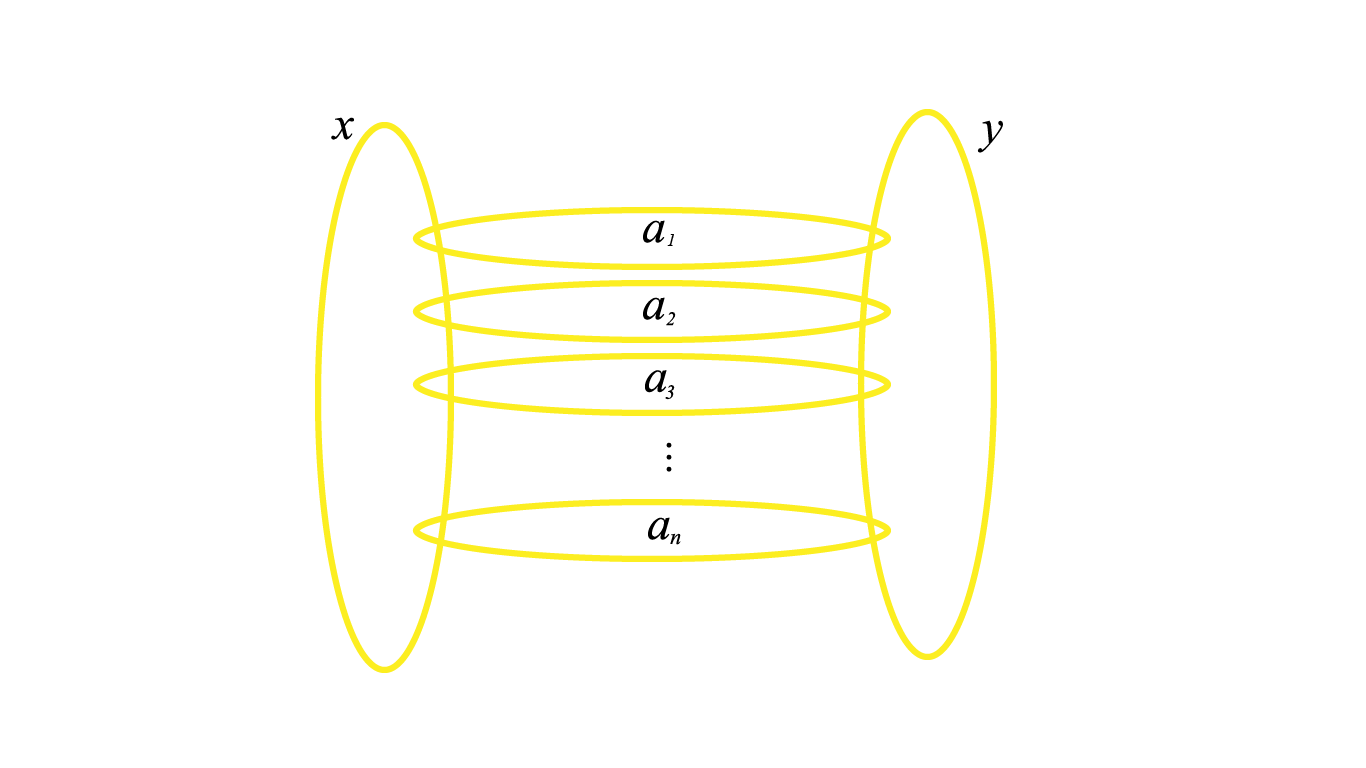
+ محدودیت زمان: ۱ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- یک زنجیر مانند شکل زیر داریم:  این زنجیر دو حلقه جدا از هم به ارزش $x$ و $y$ تومان دارد که با $n$ زنجیر کوچک‌تر و دو به دو جدا از هم به یکدیگر متصل شده‌اند. ارزش حلقه‌ی کوچک‌ها به ترتیب $a_1, a_2, \dots, a_n\,$ تومان است. می‌خواهیم مقدارهای $x$ و $y$‌ و $a_1, a_2, \dots, a_n\,$ را طوری تعیین کنیم که بتوانیم همه‌ی مبالغ $1$ تا $x + y + a_1 + \dots + a_n$ را پرداخت کنیم. برای پرداخت اگر تصمیم بگیریم تعدادی از حلقه‌ها را بدهیم فرض کنید بقیه‌ی حلقه‌ها ناپدید می‌شوند و ما می‌توانیم حلقه‌های باقی‌مانده را پرداخت کنیم. همچنین می‌خواهیم حلقه‌هایی که به یک نفر می‌دهیم باید همبند باشد یعنی به دو قسمت تبدیل نشود و حلقه‌ها تو در توی هم باشند. فرض کنید شکستن یا داخل هم کردن حلقه‌ها ممکن نیست. از شما می‌خوهیم طوری عدد گذاری کنید که حداکثر مبلغ ممکن را پرداخت کنیم. برای بهتر فهمیدن خواسته‌ی سوال، مثال‌ها را ببیند. # ورودی در تنها سطر ورودی، عدد صحیح و مثبت $n$ داده می‌شود. $$2 \leq n \leq 50 $$ # خروجی در سطر اول خروجی، دو مقدار طبیعی $x$ و $y$ را چاپ کنید. در سطر دوم خروجی، $n$ عدد طبیعی $a_1, a_2, \dots, a_n\,$ با فاصله از هم چاپ کنید. $$1 \leq x, y, a_1, a_2, \dots, a_n \leq 10^{18}$$ اگر چند جواب مختلف وجود دارد یکی را به دلخواه چاپ کنید. # مثال‌ها ## ورودی نمونه ۱ ``` 2 ```` ## خروجی نمونه ۱ ``` 1 2 3 7 ```` اگر عددگذاری را مانند شکل زیر انجام دهیم همه‌ی مبالغ از ۱ تا ۱۳ تومان قابل پرداخت با تعدادی حلقه‌ی متصل به‌هم است.  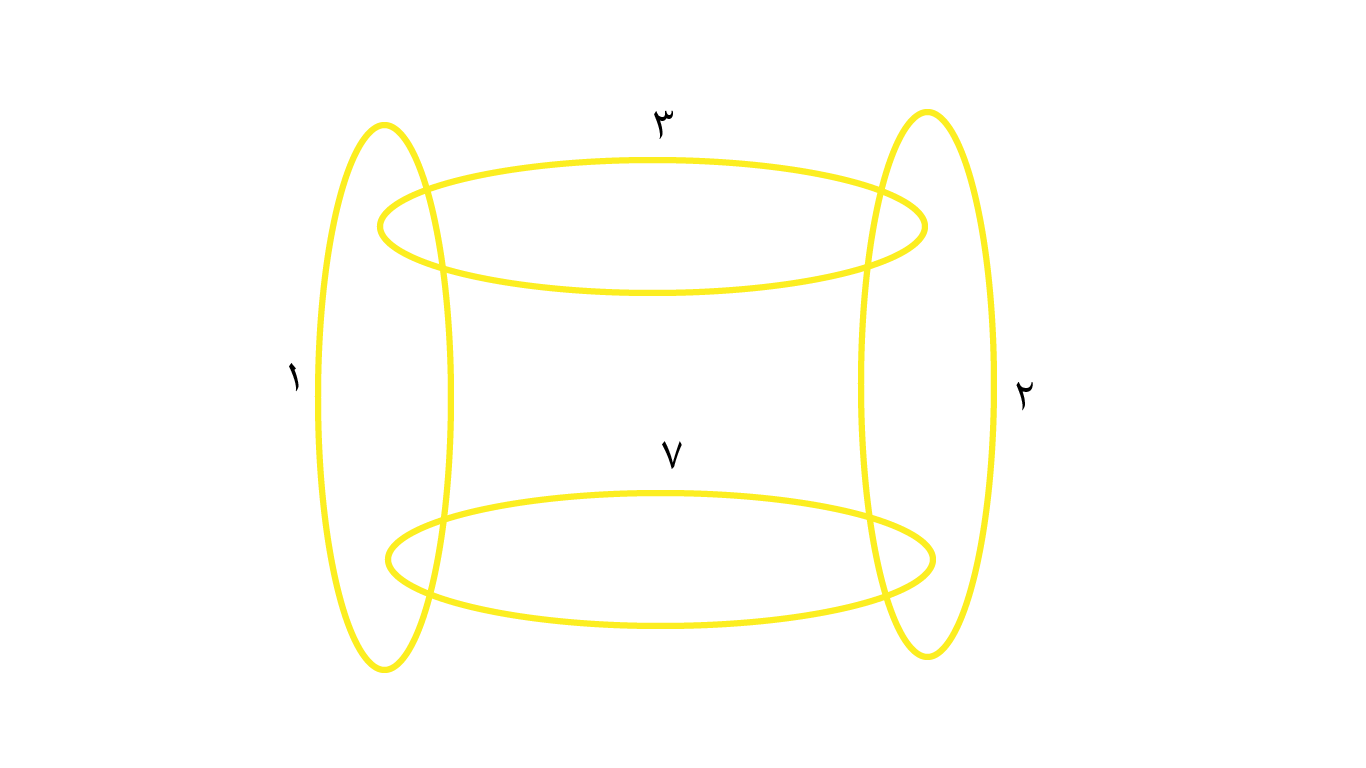+ برای پرداخت ۱ تومان حلقه‌ی ۱ را می‌دهیم. + برای پرداخت ۲ تومان حلقه‌ی ۲ را می‌دهیم. + برای پرداخت ۳ تومان حلقه‌ی ۳ را می‌دهیم. + برای پرداخت ۴ تومان حلقه‌های ۱ و ۳ را می‌دهیم. + برای پرداخت ۵ تومان حلقه‌های ۲ و ۳ را می‌دهیم. + برای پرداخت ۶ تومان حلقه‌های ۱، ۲ و ۳ را می‌دهیم. + برای پرداخت ۷ تومان حلقه‌ی ۷ را می‌دهیم. + برای پرداخت ۸ تومان حلقه‌های ۱ و ۷ را می‌دهیم. + برای پرداخت ۹ تومان حلقه‌های ۲ و ۷ را می‌دهیم. + برای پرداخت ۱۰ تومان حلقه‌های ۱، ۲ و ۷ را می‌دهیم. + برای پرداخت ۱۱ تومان حلقه‌های ۱، ۳ و ۷ را می‌دهیم. + برای پرداخت ۱۲ تومان حلقه‌های ۲، ۳ و ۷ را می‌دهیم. + برای پرداخت ۱۳ تومان حلقه‌های ۱، ۲، ۳ و ۷ را می‌دهیم همچنین ۱۳ بیشترین عددی است که می‌توانیم پرداخت کنیم. توجه کنید برای پرداخت ۳ تومان نمی‌توانستیم حلقه‌ی ۱ و ۲ را بدهیم چون دو تکه می‌شود و شرط همبندی را ندارد.