+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
آقای جلالیان یک تاس دارد. این تاس یک مکعب است که شامل ۶ وجه بوده و روی هر وجه آن یک عدد از ۱ تا ۶ هر کدام دقیقاً یکبار نوشته شده است.
در شکل زیر، باز شدهی تاس و نحوهی قرار گرفتن اعداد روی وجههای مختلف نمایش داده شده است:
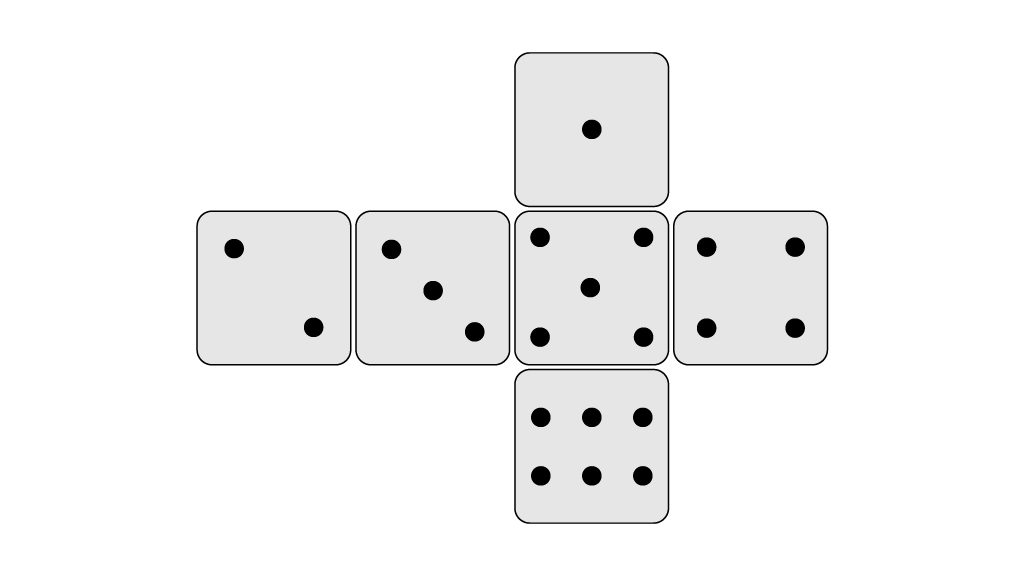
برای آقای جلالیان جالب است بداند که اگر این تاس را به شکل مکعب در نظر بگیریم، عدد نوشته شده بر روی هر وجه، در مقابل کدام عدد قرار میگیرد. به عبارتی دیگر، میخواهد بداند در شکل مکعبی، وجه مقابل هر عدد چیست.
برای همین آقای جلالیان به شما عدد $n$ از ۱ تا ۶ را میدهد و از شما میخواهد برنامهای بنویسید که عدد وجه مقابل $n$ را چاپ کنید.
# ورودی
در تنها سطر ورودی، عدد صحیح $n$ داده میشود.
$$1\leq n \leq 6$$
# خروجی
در تنها سطر خروجی عدد صحیح $m$ که عدد روبهروی $n$ در تاس آقای جلالیان است را چاپ کنید.
# مثالها
## ورودی نمونه ۱
```
1
````
## خروجی نمونه ۱
```
6
````
<details class="green">
<summary>
**توضیح نمونه ۱**
</summary>
همانطور که در تصویر زیر مشخص است، $m = 6$ روبهروی $n = 1$ قرار دارد.
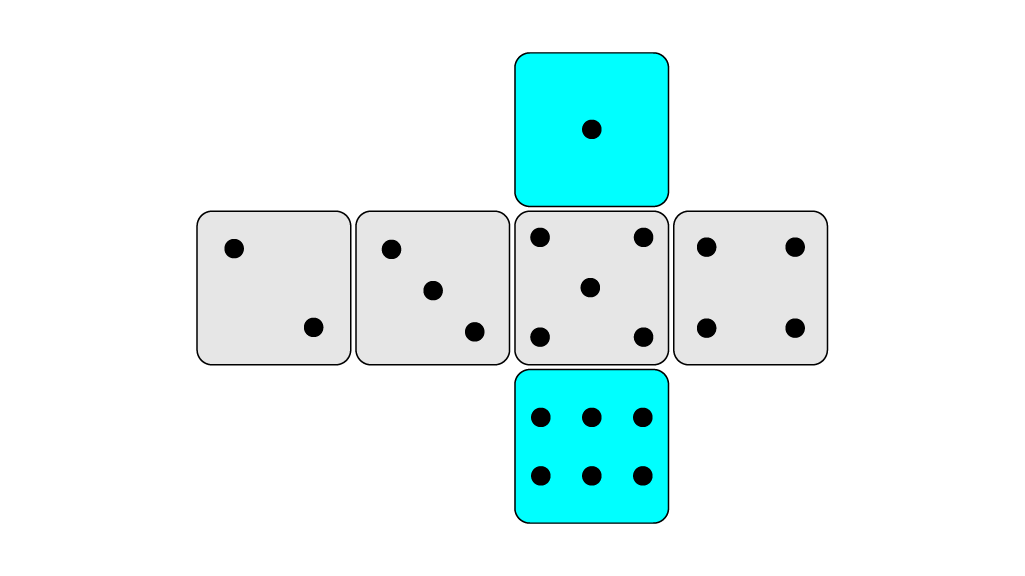
</details>
## ورودی نمونه ۲
```
5
````
## خروجی نمونه ۲
```
2
````
<details class="green">
<summary>
**توضیح نمونه ۲**
</summary>
همانطور که در تصویر زیر مشخص است، $m = 2$ روبهروی $n = 5$ قرار دارد.
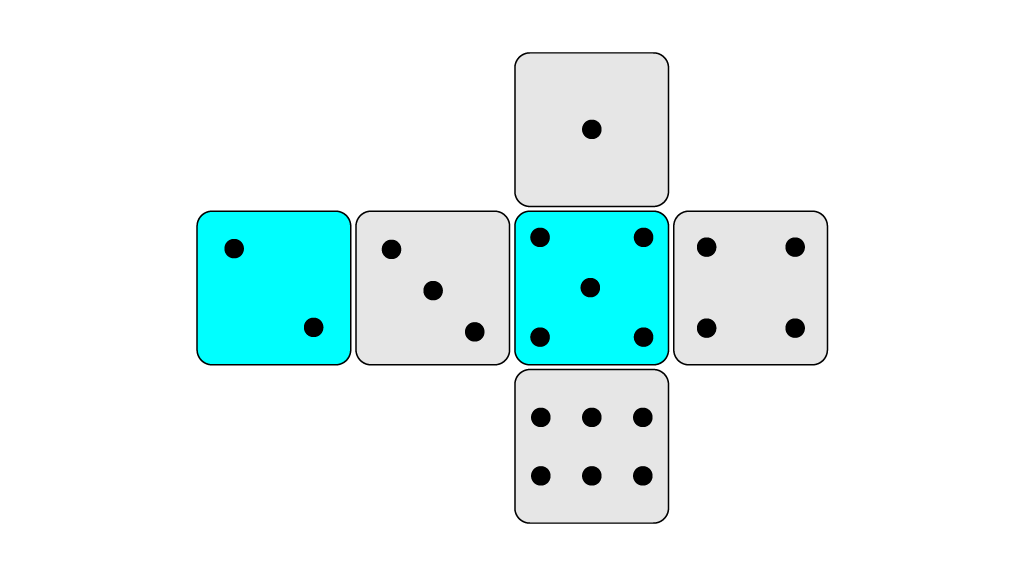
</details>
<details class="red">
<summary>
**اشتباهات متداول**
</summary>
<details class="red">
<summary>
**چک کردن شرایط ورودی مسئله**
</summary>
نیازی نیست چک کنید شرایط گفته شده در ورودی برقرار است یا نه. توضیحات محدودیتها فقط برای آگاهی شما دربارهی تستها و محدودیتهای مسئله است و قطعاً در ورودیهای داده شده به برنامهی شما رعایت میشوند. پس نیازی نیست بنویسید:
```python
if 1 <= n <= 100:
# answer of problem
else:
# print('invalid input')
```
</details>
<details class="red">
<summary>
**ابتدا همهی ورودی را گرفتن و در نهایت همهی خروجی را چاپ کردن**
</summary>
شما میتوانید لابهلای دریافت ورودی، خروجی دهید. پس نیازی نیست ابتدا همهی ورودیها را دریافت کنید و در نهایت همهی خروجیها را چاپ کنید.
</details>
<details class="red">
<summary>
**چاپ موارد اضافه برای دریافت ورودی**
</summary>
لطفاً از چاپ کردن موارد اضافه مثل `please enter a number` برای دریافت ورودی پرهیز کنید. برای مثال در زبان پایتون نباید بنویسید:
```python
input('please enter:')
```
</details>
<details class="red">
<summary>
**چند فایلی کد زدن**
</summary>
برای زبانهایی مثل جاوا نباید در بالای کد شما آدرس پکیج داده شود. برای مثال در بالای کد خود نباید بنویسید:
```java
package ir.quera.contest;
```
</details>
<details class="red">
<summary>
**استفاده از چند `Scanner` برای دریافت ورودی**
</summary>
در زبان جاوا، باید فقط یک شئ از جنس `Scanner` تعریف کنید و همهی ورودیها را با آن دریافت کنید.
</details>
<details class="red">
<summary>
**نحوهی دریافت ورودی و چاپ کردن خروجی**
</summary>
برای آشنایی بیشتر برای نحوهی دریافت ورودی و چاپ کردن خروجی این [لینک](https://quera.org/course/assignments/2693/problems/8774) را مطالعه کنید.
</details>
تاس آقای جلالیان
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
آقای جلالیان یک تقویم جلالی عجیب روی میز کارش دارد. تقویم او از دو تاس مکعبی با ۶ وجه تشکیل شده است. اما روی این تاسها لزوما اعداد `1`، `2`، ...، `6` نوشته نشده است بلکه ممکن است روی هر وجه یک رقم از `0`، `1`، ...، `9` نوشته شده باشد.
آقای جلالیان از روز اولی که وارد شرکت شد، با تاسهایش روزشماری میکند تا بداند تا امروز چند روز از اولین روز کاریاش در شرکت میگذرد.

روش استفاده آقای جلالیان از تاسهایش برای نشان دادن شماره روز به این صورت است که با **یک تاس** اعداد یک رقمی و با کنارهم گذاشتن دوتاس اعداد دو رقمی ساخته میشوند. مثلاً اگر تاس سمت چپ رقم `3` و تاس سمت راست رقم `2` را نشان دهد یعنی در روز `32`ام هستیم.
آقای جلالیان میداند که قرار است دقیقاً تا روز $n$ام در شرکت بماند که $n$ عددی حداکثر دو رقمی است. او تصمیم دارد دو تاس خام بگیرد و روی وجههای تاس اول ارقام $a_1, a_2, \dots, a_6\,$ و روی وجههای تاس دوم ارقام $b_1, b_2, \dots, b_6\,$ را بنویسد به طوری که بتواند در همهی روزهای ۱ تا $n$ شمارهی روز را روی میزش نمایش دهد.
به آقای جلالیان کمک کنید تا مقدارهای مناسب برای $a_1, a_2, \dots, a_6\,$ و $b_1, b_2, \dots, b_6\,$ را پیدا کند یا به او بگویید هیچ روشی برای انجام این کار وجود ندارد.
# ورودی
در تنها سطر ورودی، یک عدد طبیعی $n$ داده میشود که نشاندهنده شماره روز آخرین روز کاری آقای جلالیان است.
$$1\leq n \leq 99$$
# خروجی
در صورتی که این کار امکان پذیر نبود `-1` چاپ کنید. و در غیر این صورت خروجی شامل دو سطر خواهد بود.
در سطر اول خروجی ۶ رقم $a_1, a_2, \dots, a_6\,$ با فاصله از هم چاپ کنید که هر رقم نشاندهنده یک رقم روی یکی از وجههای تاس اول است و به همین شکل در سطر دوم خروجی ۶ رقم $b_1, b_2, \dots, b_6\,$ با فاصله از هم چاپ کنید که هر رقم نشاندهنده یک رقم روی یکی از وجههای تاس دوم است.
**اگر چند جواب برای این مسئله وجود دارد، یکی را به دلخواه چاپ کنید.**
# مثالها
## ورودی نمونه ۱
```
10
```
## خروجی نمونه ۱
```
0 0 5 3 2 4
1 1 6 7 8 9
```
در اینجا آقای جلالیان روی وجههای تاس اول ارقام `0`، `0`، `5`، `3`، `2` و `4` و روی وجههای تاس دوم ارقام `1`، `1`، `6`، `7`، `8` و `9` را نوشته است.
چون همهی ارقام `1` تا `9` حداقل یکبار ظاهر شدهاند، پس برای نشاندادن روزهای ۱ تا ۹ مشکلی نیست.
برای روز ۱۰ام، میتواند `1` را از تاس دوم و `0` را از تاس اول بردارد.
## ورودی نمونه ۲
```
99
```
## خروجی نمونه ۲
```
-1
```
آقای جلالیان هیچ روشی ندارد که طوری ارقام ۰ تا ۹ را روی وجههای دو تاس طوری قرار دهد که همهی اعداد ۱ تا ۹۹ قابل نمایش باشند. بنابراین پاسخ `-1` است.
تقویم آقای جلالیان
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
شهر کدکاپ به صورت یک صفحهی مختصات دو بعدی است. در این شهر آدمها همیشه در نقطههایی مثل $(x,y)$ قرار دارند که $x$ و $y$ دو عدد صحیح هستند. منظور از فاصلهی دو نقطهی $(x, y)$ و $(a,b)$ عدد $|a - x| + |b - y|$ است.
یک پلیس در نقطهی $(0, 0)$ قرار دارد. یک دزد از بانکی که در نقطهی $(d, 0)$ قرار دارد دزدی میکند. آژیر خطر به صدا در میآید و بازی دزد و پلیس شروع میشود.

دزد در هر ثانیه یا در نقطهی قبلی میماند یا به یکی از نقطههای بالا، پایین، چپ یا راست میرود. یعنی اگر در نقطهی $(x, y)$ باشد در ثانیهی بعدی در یکی از نقطههای $(x, y)$، $(x + 1, y)$، $(x - 1, y)$، $(x, y + 1)$ یا $(x, y - 1)$ قرار دارد. در واقع دزد در یک ثانیه میتواند به نقطهای که فاصلهی آن حداکثر ۱ است برود.
پلیس در هر ثانیه میتواند به نقطهای که فاصلهی آن حداکثر ۲ است برود. میدانیم پلیس همیشه موقعیت دزد را میداند. او همیشه بر اساس موقعیت دزد نقطهای که یک ثانیه بعد در آن است را مشخص میکند. اگر اکنون پلیس در نقطهی $(x, y)$ و دزد نقطهی $(a, b)$ باشد:
+ اگر $|x - a| \gt |y - b|$ باشد پلیس به یکی از نقطههای $(x + 2, y)$، $(x + 1, y )$، $(x - 1, y)$ یا $(x - 2, y)$ میرود که به دزد نزدیکتر است.
+ اگر $|x - a| \lt |y - b|$ باشد پلیس به یکی از نقطههای $(x, y+2)$، $(x,y+1)$، $(x,y-1)$ یا $(x,y-2)$ میرود که به دزد نزدیکتر است.
+ اگر $|x - a| = |y - b|$ باشد پلیس به یکی از نقطههای $(x + 1,y+1)$، $(x-1,y+1)$، $(x+1,y-1)$ یا $(x-1,y-1)$ میرود.
برای راحتی کار فرض کنید آنها **یکی در میان حرکتشان** را انجام میدهند یعنی ابتدا پلیس، سپس دزد، مجدداً پلیس، سپس دزد و... . با توجه به قوانین حرکت آنها میتوان فهمید بالاخره پلیس به نقطهای که دزد در آن قرار دارد میرسد و دزد دستگیر میشود.
حال شهردار کدکاپ میخواهد بداند با توجه به حالتهای مختلفی که حرکت دزد دارد، چند نقطه در صفحه وجود دارد که ممکن است در آن نقطه دزد توسط پلیس دستگیر شود.
برای بهتر متوجه شدن خواستهی سوال به توضیح نمونهها توجه کنید.
# ورودی
در سطر اول ورودی، عدد صحیح و مثبت $t$ آمده که تعداد سناریوها را نشان میدهد.
$$1 \leq t \leq 100 \, 000$$
در $t$ سطر بعدی در هر سطر عدد صحیح و مثبت $d$ که موقعیت دزد را نشان میدهد داده میشود.
$$1 \leq d \leq 10^9$$
# خروجی
خروجی $t$ سطر دارد که برای هر سناریو، تعداد نقاطی که دزد ممکن است در آن دستگیر شود را چاپ کنید.
# مثالها
## ورودی نمونه ۱
```
3
2
5
9
````
## خروجی نمونه ۱
```
1
21
85
````
<details class="green">
<summary>
**توضیح نمونه ۱**
</summary>
در این سناریو پلیس در نقطهی $(0,0)$ و دزد در نقطهی $(2,0)$ قرار دارد.

در ثانیهی اول پلیس $|2 - 0| \gt |0 - 0|$ را محاسبه کرده و تصمیم میگیرد به یکی از نقاط $(2,0)$، $(1,0)$، $(-1,0)$ یا $(-2,0)$ برود که به دزد نزدیکتر است. از آنجایی که دزد در نقطهی $(2,0)$ قرار دارد قبل از اینکه حرکت کند دستگیر میشود.
چون فقط یک نقطه وجود دارد که دزد ممکن است در آن دستگیر شود، پاسخ برابر ۱ است.
</details>
<details class="green">
<summary>
**توضیح نمونه ۲**
</summary>
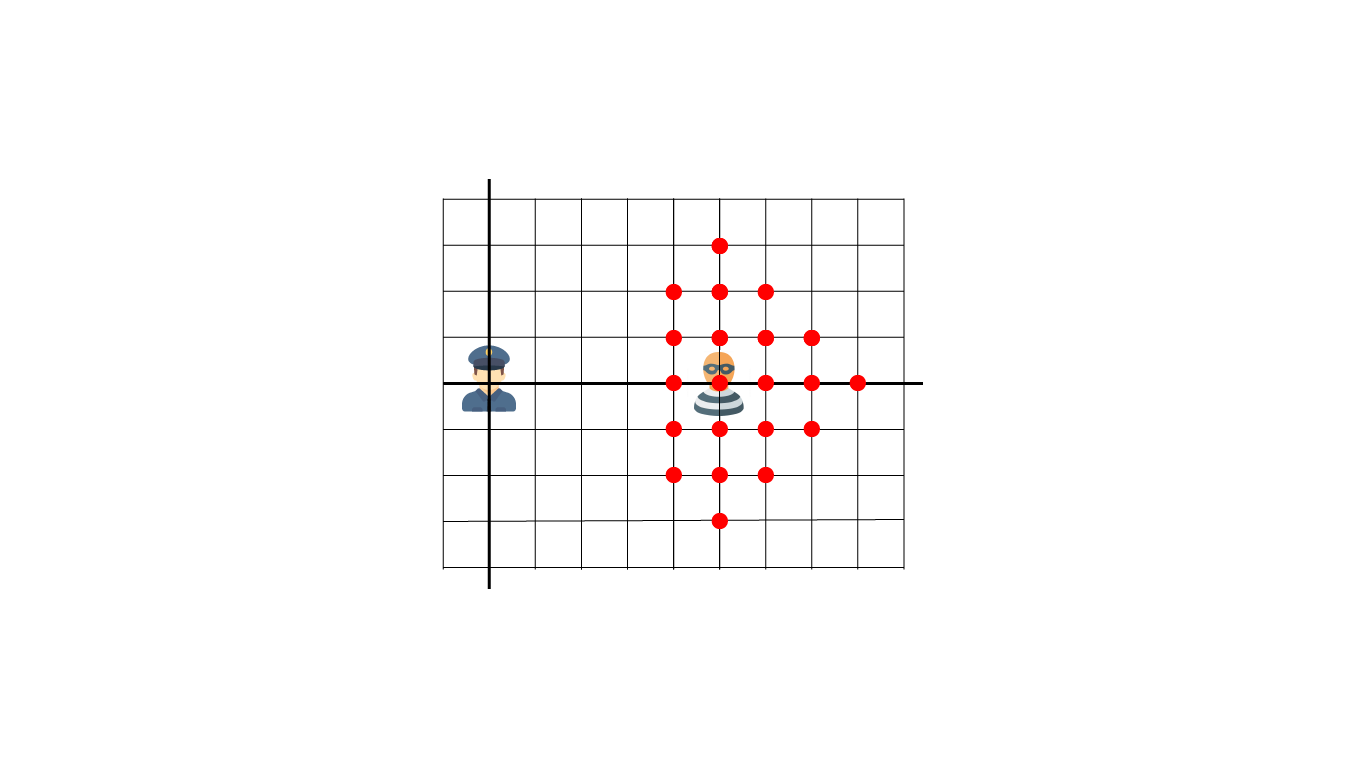
در ثانیهی اول پلیس $|5 - 0| \gt |0 - 0|$ را محاسبه کرده و تصمیم میگیرد به یکی از نقاط $(2,0)$، $(1,0)$، $(-1,0)$ یا $(-2,0)$ برود که به دزد نزدیکتر است. از آنجایی که نقطهی $(2,0)$ به دزد نزدیکتر است آن را انتخاب میکند. سپس نوبت دزد است که در ثانیهی اول حرکت کند. فرض کنید او تصمیم میگیرد به نقطهی بالایی یعنی $(5,1)$ برود.
در ثانیهی دوم پلیس $|5-2| \gt |0 - 1|$ را محاسبه کرده و تصمیم میگیرد به یکی از نقاط $(4,0)$، $(3,0)$، $(1,0)$ یا $(0,0)$ برود که به دزد نزیکتر است. از آنجایی که نقطهی $(4,0)$ به دزد نزدیکتر است آن را انتخاب میکند. سپس نوبت دزد است که در ثانیهی دوم حرکت کند. فرض کنید تصمیم میگیرد سر جای خودش یعنی $(5,1)$ بماند.
در ثانیهی سوم پلیس $|4-5| = |1-0|$ را محاسبه میکند و تصمیم میگیرد به یکی از نقاط $(5,1)$، $(5,-1)$، $(3,1)$ یا $(3,-1)$ برود که به دزد نزدیکتر است. از آنجایی که دزد در نقطهی $(5,1)$ قرار دارد قبل از اینکه حرکت کند دستگیر میشود.
پس نقطهی $(5,1)$ یکی از نقاط دستگیری دزد است. با توجه به حالتهای مختلف برای تصمیمگیری حرکت دزد، همهی نقاط قرمز مشخص شده در شکل بالا ممکن است محل دستگیری دزد باشد.
</details>
<details class="green">
<summary>
**توضیح نمونه ۳**
</summary>
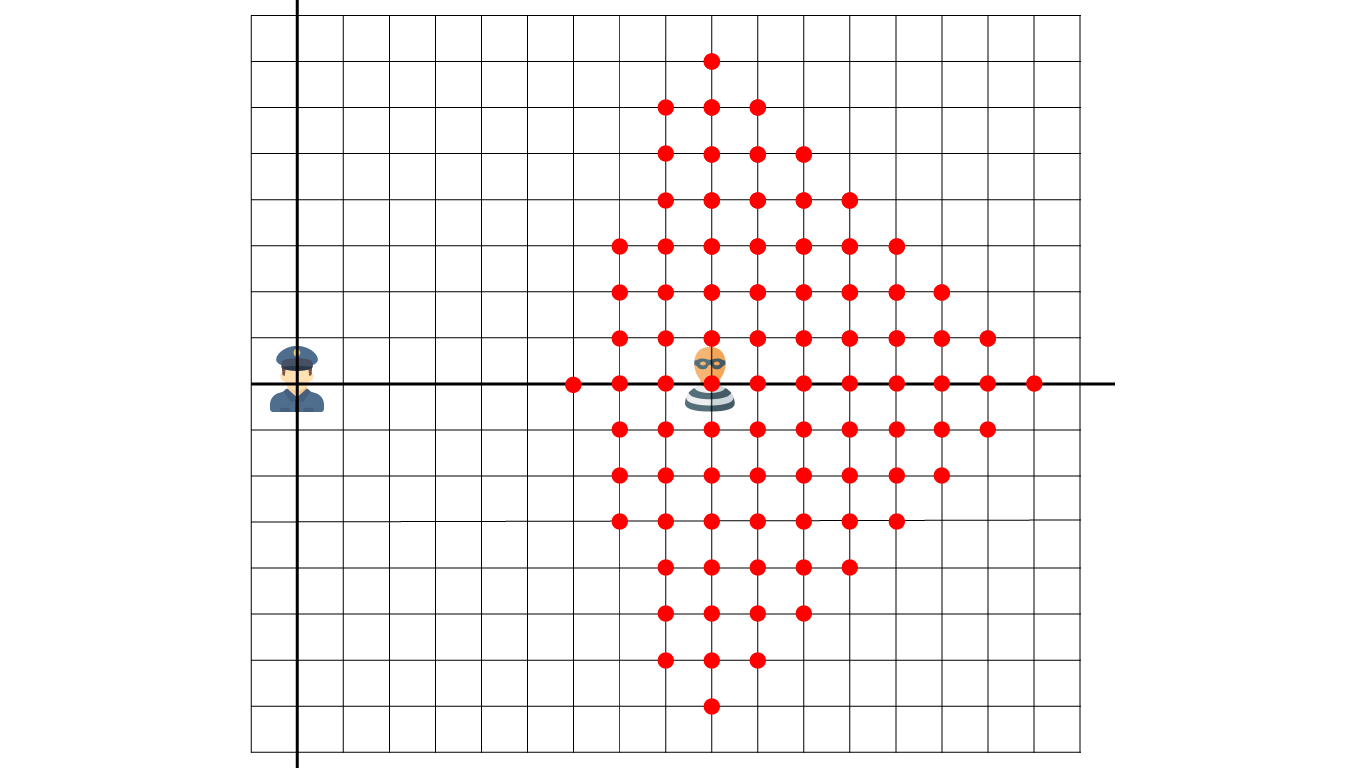
مشابه قبل همهی نقاطی که محل دستگیری دزد هستند در شکل بالا نشان داده شده.
</details>
دزد و پلیس
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
رئیس جمهور کشور کدکاپ میخواهد به هر استاندار تعدادی سکه جایزه بدهد. او میخواهد برای ایجاد رقابت بین استانها، به استاندارهایی که در دو استان همسایه قرار دارند تعداد سکه متفاوتی جایزه بدهد.

جادههای این کشور دو طرفهاند و بین دو استان کشیده شدهاند. میدانیم اگر از هر استان کشور کدکاپ شروع کنیم میتوانیم با رفتن به استانهای همسایه، به تمام استانهای کشور برسیم. همچنین تعداد جادهها بسیار کم است و به اندازه حداقل تعداد جاده برای رسیدن از تمام استانها به استانهای دیگر طراحی شده است. میتوان اثبات کرد که همیشه تعداد جادهها یکی کمتر از تعداد استانها است.
کمترین تعداد سکهای که رئیس جمهور برای جایزه دادن به استاندارها باید خرج کند به صورتی که استاندارهای هیچ دو استان مجاوری تعداد سکه برابر دریافت نکرده باشند، را محاسبه کنید.
# ورودی
در سطر اول ورودی، عدد صحیح و مثبت $t$ آمده که تعداد سناریوها را نشان میدهد. سپس در ادامه برای هر سناریو به ترتیب ورودیها داده میشوند.
$$1 \leq t \leq 300 \, 000$$
در سطر اول هر سناریو عدد صحیح و مثبت $n$ که نشانگر تعداد شهرها در سناریو $i$ام است ورودی داده میشود.
سپس در $n - 1$ خط بعدی جادههای کشور ورودی داده میشوند، در هر خط دو عدد صحیح و مثبت $v_i$ و $u_i$ داده میشود که دو استان مبدا و مقصد جاده را مشخص میکنند.
$$1 \leq n \leq 300 \, 000$$
$$1 \leq u_i, v_i \leq n$$
**تضمین میشود که مجموع $n$ روی همهی سناریوها حداکثر ۳۰۰،۰۰۰ باشد.**
# خروجی
خروجی $t$ سطر دارد که برای هر سناریو، در یک خط کمترین میزان سکه برای جایزه دادن به کل استانها را باید چاپ کنید.
# مثالها
## ورودی نمونه ۱
```
2
2
2 1
8
7 3
4 6
1 7
5 4
7 4
2 7
8 4
````
## خروجی نمونه ۱
```
3
11
````
<details class="green">
<summary>
**توضیح نمونه ۱**
</summary>
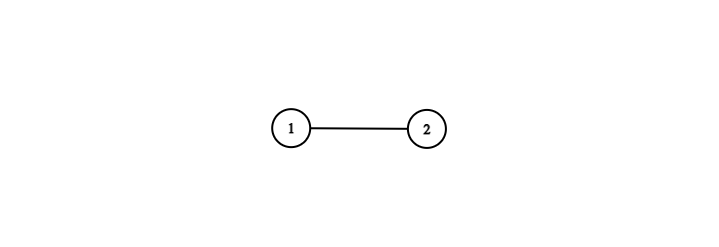
اگر به استان ۱، $1$ سکه و به استان ۲، $2$ سکه داده شود، هیچ دو استان مجاوری تعداد یکسانی سکه دریافت نمیکنند و این کمترین مجموع سکه ممکن را دارد. بنابراین پاسخ برابر $1 + 2 = 3$ است.
</details>
<details class="green">
<summary>
**توضیح نمونه ۲**
</summary>
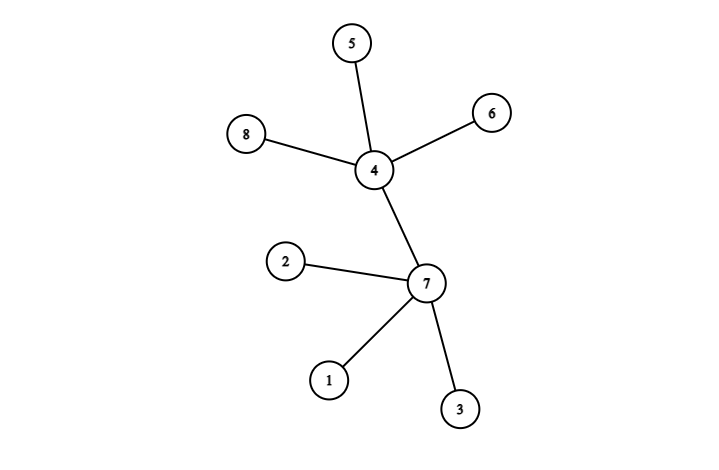
اگر به استان ۱، ۲، ۳، ۵، ۶ و ۸ $1$ سکه و به استان ۴، $2$ سکه و به استان ۷، $3$ سکه داده شود، هیچ دو استان مجاوری تعداد یکسانی سکه دریافت نمیکنند و این کمترین مجموع سکه ممکن را دارد. بنابراین پاسخ برابر $6 \times 1 + 2 + 3 = 11$ است.
</details>
جایزه به استاندار
+ محدودیت زمان: ۱.۵ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
مریم آرایه $n$ عضوی $a=[a_1,a_2,...,a_n]$ را دارد. او میخواهد **امتیاز** $q$ تا از زیربازههای این آرایه را پیدا کند. **امتیاز** یک زیربازه برابر با تعداد اعدادی است که نسبت به این زیربازه **خوشحال** هستند.
همچنین میدانیم عدد $k$ نسبت به زیربازهی $[a_{l},a_{{l}+1},a_{{l}+2},...,a_{r}]$ **خوشحال** است اگر عدد $k$ دقیقاً $x$ بار در زیربازه آمده باشد که $cl_k \leq x \leq cr_k$ باشد.

برای مثال اگر $a$ برابر با $[1,2,1]$ باشد و $cl_1=cr_1=1$ عدد $1$ نسبت به زیربازهی $1$ تا $2$ ($[1,2]$) **خوشحال** است چون یک بار در این بازه آمده است ولی نسبت به زیربازهی $1$ تا $3$ ($[1,2,1]$) **خوشحال** نیست چون دو بار در این بازه آمده است و $cr_1 < 2$.
# ورودی
در سطر اول ورودی، سه طبیعی $n$ که طول آرایه، $m$ که حداکثر عدد آرایه و $q$ که تعداد زیربازههایی است که مریم میخواهد امتیاز آنها را بداند.
$$1\leq n, m, q \leq 300\,000$$
در سطر بعدی $n$ عدد $a_1, a_2, \dots, a_n\,$ آمده که اعضای آرایه را نشان میدهند.
$$1 \leq a_i \leq m$$
در $m$ سطر بعدی، در سطر $i$ام بعدی دو عدد $cl_i$ و $cr_i$ آمده است.
$$1\leq cl_i \leq cr_i \leq 300\,000$$
در هر کدام از $q$ سطر بعدی دو عدد آمده است که بازهای را که مریم میخواهد امتیاز آن را پیدا کند. پس در سطر $i$ام از این $q$ سطر بعدی دو عدد $l_i, r_i$ آمده است که مریم امتیاز
$[a_{l_i},a_{{l_i}+1},a_{{l_i}+2},...,a_{r_i}]\quad$
را میخواهد پیدا کند.
# خروجی
در تنها سطر خروجی $q$ عدد چاپ کنید که عدد $i$ام امتیاز زیربازهی $[a_{l_i},a_{{l_i}+1},a_{{l_i}+2},...,a_{r_i}]\quad$ است.
# مثالها
## ورودی نمونه ۱
```
6 3 4
1 2 3 1 2 1
2 3
1 1
1 1
1 6
1 4
3 5
4 4
````
## خروجی نمونه ۱
```
2 3 2 0
````
در این مثال آرایه $a$ به صورت
$[1, 2, 3, 1, 2, 1]$
است.
عدد `1` زمانی خوشحال است که بین $[2, 3]$ بار تکرار شود. عدد `2` و `3` زمانی خوشحال هستند که دقیقاً $1$ بار ظاهر شوند.
+ زیر بازهی اول از ۱ تا ۶ (یعنی $[1, 2, 3, 1, 2, 1]$) است. که اعداد ۱ و ۳ خوشحال هستند پس امتیاز آن ۲ است.
+ زیر بازهی دوم از ۱ تا ۴ (یعنی $[3, 1, 2, 1]$) است. که اعداد ۱، ۲ و ۳ خوشحال هستند پس امتیاز آن ۳ است.
+ زیر بازهی سوم از ۳ تا ۵ (یعنی $[3, 1, 2]$) است. که اعداد ۲ و ۳ خوشحال هستند پس امتیاز آن ۲ است.
+ زیر بازهی چهارم از ۴ تا ۴ (یعنی $[1]$) است. که هیچ عددی خوشحال نیست، پس امتیاز آن ۰ است.
امتیاز آرایه
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
سارا در مرکز محور مختصات ایستاده است و تکان نمیخورد. اطراف او $n$ سیبل وجود دارد که او میخواهد به سمت آنها تیر اندازی کند. سارا میخواهد با کمترین تعداد گلولهی ممکن تمام سیبلها را سوراخ کند. سارا برای اینکار به حداقل چند گلوله نیاز دارد؟
همچنین میدانیم گلولههای سارا بسیار با کیفیت هستند و بعد از برخورد با یک سیبل بدون تغییر جهت به مسیر خود ادامه میدهند و اگر باز هم سیبلی در مسیرشان بود آنها را هم سوراخ میکنند. همچنین اگر مسیر یک گلوله تنها با نقطهی گوشهی یک سیبل برخورد داشته باشد (مماس باشد) آن سیبل سوراخ میشود.
در شکل زیر سیبلها با رنگ قرمز مشخص شدهاند و یک خط فرضی شلیک برای سارا با خط هاشور خوردهی سبز نشان داده شده است. این جهت شلیک، دو تا از سیبلها را سوراخ میکند.
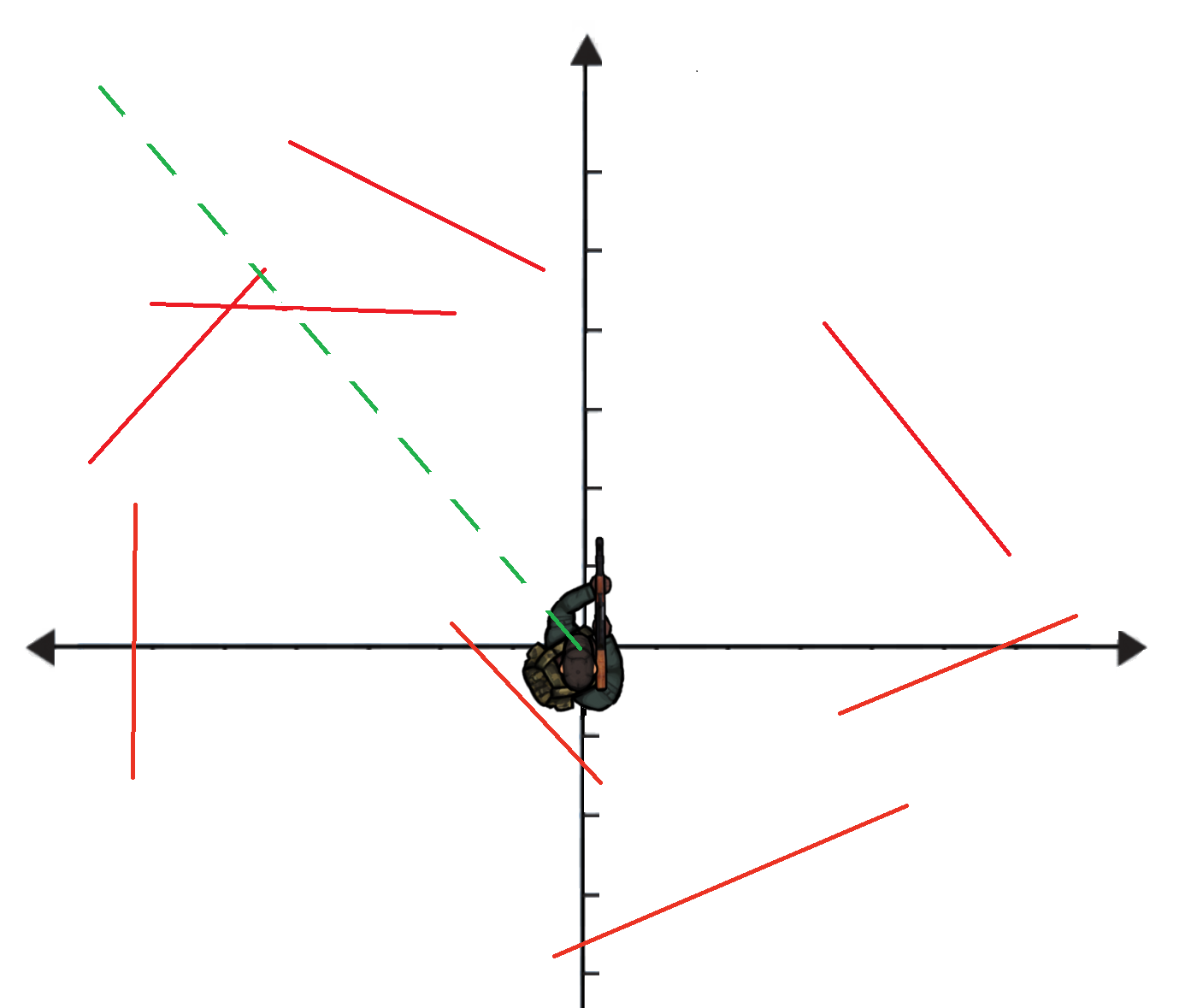
# ورودی
در سطر اول ورودی، عدد طبیعی $n$ که تعداد سیبلها است داده شده است.
$$1\leq n \leq 100\,000$$
در $t$ سطر بعدی، در هر سطر اطلاعات یک سیبل داده شده است. هر سیبل با دادن چهار عدد $x_1, y_1, x_2, y_2\,$ مشخص میشود که $(x_1,y_1)$ مختصات یک سر سیبل و $(x_2,y_2)$ مختصات سر دیگر سیبل است.
$$-10^9\leq x_1,x_2 \leq 10^9$$
$$-10^9\leq y_1,y_2 \leq 10^9$$
همچنین میدانیم هیچ سیبلی از روی سارا (نقطهی $(0, 0)$) عبور نمیکند و همچنین اگر هر سیبل را از دو طرفش ادامه دهیم این خط هم با سارا (نقطهی $(0, 0)$) برخورد نمیکنند.
# خروجی
حداقل تعداد گلولهی مورد نیاز برای سوراخ کردن تمام سیبلها را در تنها سطر خروجی چاپ کنید.
# مثالها
## ورودی نمونه ۱
```
4
0 1 1 0
2 0 0 -1
0 -3 -1 0
-5 0 0 4
````
## خروجی نمونه ۱
```
2
````
<details class="green">
<summary>
**توضیح نمونه ۱**
</summary>
اگر ۲ شلیک را مانند شکل زیر انجام دهد هر ۴ سیبل را سوراخ کرده است.
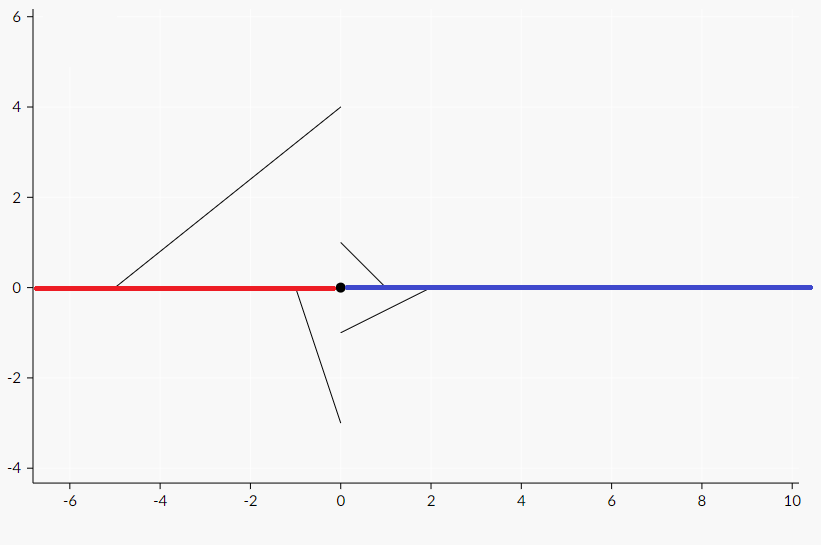
</details>
## ورودی نمونه ۲
```
6
-1 2 -2 1
-5 5 6 5
-5 -6 6 5
-5 5 -5 -6
-2 1 -2 -1
-1 2 0 2
````
## خروجی نمونه ۲
```
3
````
<details class="green">
<summary>
**توضیح نمونه ۲**
</summary>
اگر ۳ شلیک را مانند شکل زیر انجام دهد هر ۶ سیبل را سوراخ کرده است.
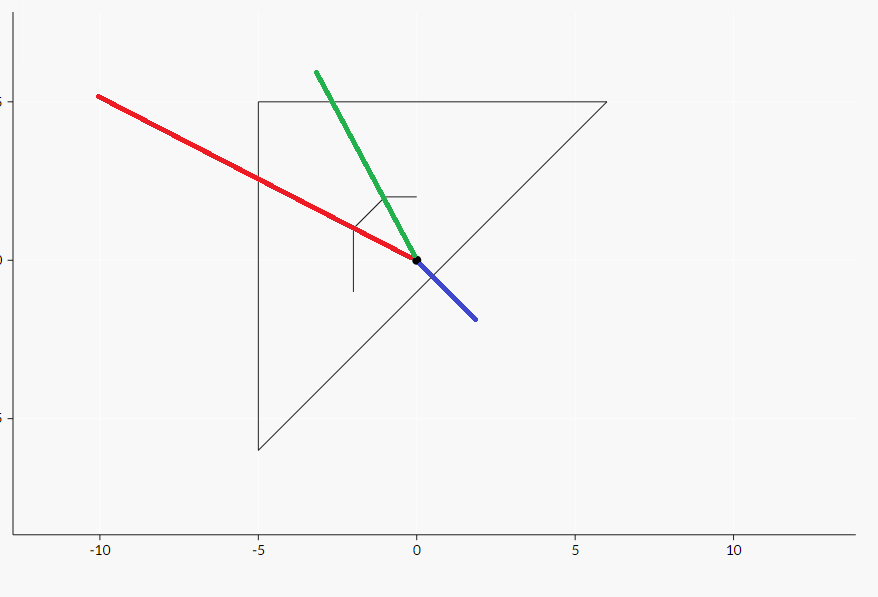
</details>