• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

با توجه به در خواست های آمده از بالا اسم سوال از الماس جادویی به سختش نکن تغییر کرد.

در جزیره آدم نخوار ها هر الماس ارزش معادل $x$ سکه طلا دارد و هر سکه طلا ارزش معادل $y$ سکه نقره دارد و هر سکه نقره ارزش معادل $z$ سکه برنز دارد. امیرحسین می خواهد $n$ الماس که در افسانه ها می گویند جادویی است را سوغاتی از جزیره خارج کند اما چون آدم های جزیره مهربان هستند زمانی که ۱ الماس امیرحسین بخرد باقی الماس ها را مجانی به او می دهند. به امیرحسین بگویید برای اینکار حداقل به چند سکه برنز نیاز دارد.

ورودی🔗

ورودی شامل $t+1$ خط است که در خط اول عدد طبیعی $t$ آمده است. $1 \le t \le 10^5$ در $t$ خط بعدی به ازای هر تست کیس ۴ متغیر $n$ و $x$ و $y$ و $z$ به ترتیب آمده است. $1 \le n, x, y, z \le 10^4$

خروجی🔗

خروجی برنامه‌ی شما باید شامل $t$ که خط $i$ام جواب تست $i$ام است.

مثال🔗

ورودی نمونه ۱🔗

2
1 1 1 1
2 2 2 3

خروجی نمونه ۱🔗

1
12

ورودی نمونه ۲🔗

1
1 2 3 4

خروجی نمونه ۲🔗

24

• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

سینا به تازگی یک تابع مشکوک در خونه‌اش پیدا کرده است و می‌خواهد خواص آن را برسی کند. این تابع یک آرایه $n$ عضوی از اعداد طبیعی $A$ و عدد طبیعی $x$ را به عنوان ورودی می‌گیرد و مقدار زیر را خروجی می‌دهد: $\sum_{i=1}^{n} {(A_i {\&} x)} - x$ که & نماد binary AND می‌باشد.

سینا آرایه $A$ را انتخاب کرده و از شما می‌خواهد طوری مقدار $x$ را انتخاب کنید که خروجی تابع بیشینه باشد.

ورودی🔗

ورودی شامل دو خط است که در خط اول آن عدد طبیعی $n$ آمده است. $1 \le n \le 10^5$ در خط دوم $n$ عدد آرایه به ترتیب با فاصله از هم آمده اند که $i$امین آن $A_i$ نام دارد. $0 \le A_i \le 10^9$

خروجی🔗

در خروجی بیشینه مقداری که تابع می تواند خروجی دهد را چاپ کنید.

مثال🔗

ورودی نمونه ۱🔗

5
8 3 12 2 13

خروجی نمونه ۱🔗

23

• محدودیت زمان: ۲ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

آرمین و پارسا عید خود را با بازی مثلثایره‌ گذراندند. در این بازی $n$ ردیف داریم که در ردیف $i$ام، $i$ تا دایره وجود دارد و این دایره‌ها مانند شکل زیر روی همدیگر قرار گرفته‌اند.

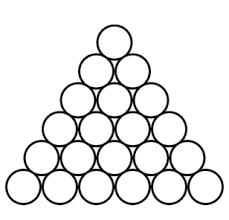
حال بازی به این صورت انجام می‌شود که ابتدا پارسا در هر ردیف دقیقا یک دایره را قرمز می‌کند و سپس آرمین از بالاترین دایره شروع می‌کند و هر دفعه از دایره‌ای که روی آن هست به دایره‌ای می‌رود که دقیقا زیر دایره فعلی هست (دو دایره این خصوصیت را دارند یعنی یا پایین چپ می‌رود یا پایین راست). این کار را تا وقتی انجام می‌دهد که به یک دایره‌ای از ردیف $n$ برسد. امتیاز آرمین برابر با تعداد دایره‌های قرمزی است که از روی آن رد می‌شود.

حال پارسا می‌خواهد امتیاز آرمین کمینه شود و آرمین می‌خواهد امتیاز خود را بیشینه کند. اگر هر دو به بهترین شکل بازی کنند امتیاز پایانی آرمین چند می‌شود؟

ورودی🔗

این مسئله $T$ تا تست کیس دارد. $1 \le T \le 10^{5}$ در هر تست کیس عدد $n$ ورودی داده می‌شود. $1 \le n \le 10^{18}$

خروجی🔗

به ازای هر تست کیس در خط‌های جدا امتیاز پایانی آرمین در صورتی که هر دو به بهترین شکل بازی کنند را خروجی دهید.

مثال🔗

ورودی نمونه ۱🔗

3
1
2
3

خروجی نمونه ۱🔗

1
2
2

• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

محمد گرافی شامل $n$ راس و $m$ یال دارد هر یال در گراف محمد یکی از $k$ رنگ موجود را دارد. پارسا برایش سوال پیش آمده است که اگر از راس $s$ در گراف شروع کند و به راس $t$ بخواهد برود حداقل چندبار باید رنگ یال هایی که می‌پیماید را عوض کند.

ورودی🔗

ورودی تنها شامل $m+2$ خط است که در خط اول آن سه عدد طبیعی $n$ و $m$ و $k$ با فاصله و به ترتیب از هم آمده است. $1 \le n, m \le 100$ $1 \le k \le 10^3$ در خط دوم دو عدد $s$ و $t$ به ترتیب آمده است. در $m$ خط بعد ۳ عدد $a_i$ و $b_i$ و $k_i$ آمده است که نشان دهنده وجود یال با رنگ $k_i$ بین $a_i$ و $b_i$ می‌باشد.

خروجی🔗

در خروجی تنها حداقل تعداد رنگ عوض کردن ها خروجی داده شود. اگر این کار امکان پذیر نبود 1- چاپ شود.

مثال🔗

ورودی نمونه ۱🔗

3 2 2
1 3
1 2 1
2 3 2

خروجی نمونه ۱🔗

1

ورودی نمونه ۲🔗

4 4 2
1 4
1 2 1
2 3 1
3 4 1
1 3 2

خروجی نمونه ۲🔗

0

ورودی نمونه ۳🔗

4 3 2
1 4
1 2 1
2 3 2
3 4 1

خروجی نمونه ۳🔗

2

• محدودیت زمان: ۳ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

آرمین، پارسا و محمد برای مسابقه‌ی الگوکاپ دچار کمبود سوال شده‌اند و نمی‌توانند دیگر سوالی طرح کنند. آن‌ها تصمیم گرفتند که سوال از اشخاص دیگر بخرند. $n$ نفر سوال می‌فروشند و مبلغی به ازای سوال‌ها دریافت می‌کنند.

نفر $i$ ام اولین سوال خود را به مبلغ $a_i$ می‌فروشد و به ازای هر سوال بعدی به مقدار $b_i$ به هزینه‌ی قبلی خود اضافه می‌کند به عبارت دیگر نفر $i$ ام $x$ امین سوال خود را به قیمت $a_i + x \times b_i$ می‌فروشد.

حال آرمین، پارسا و محمد مبلغ $m$ پول دارند. بیشترین تعداد سوالی که می‌توانند بخرند چقدر است.

ورودی🔗

ورودی شامل سه خط است که در خط اول آن دو عدد طبیعی $n$ و $m$ با فاصله از هم آمده است. $1 \le n \le 10^5$ $1 \le m \le 10^{18}$ در خط دوم آن $n$ عدد طبیعی با فاصله از هم آمده است که $i$امین آن $a_i$ است.

در خط سوم آن $n$ عدد طبیعی با فاصله از هم آمده است که $i$امین آن $b_i$ است.

$1 \le a_i, b_i\le 10^{18}$

خروجی🔗

خروجی برنامه‌ی شما باید شامل یک عدد باشد که این عدد برابر بیشترین تعداد سوال است که آرمین، پارسا و محمد می‌توانند بخرند.

مثال🔗

ورودی نمونه ۱🔗

3 10
1 2 3 
1 1 1

خروجی نمونه ۱🔗

4

• محدودیت زمان: ۴ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

تازگیا به سینا و داداشش زمین ارث رسیده و سینا به عنوان برادر بزرگتر باید یک قسمت دلخواه از زمین رو برای خودش انتخاب کنه. زمین به شکل یک مستطیل $n \times m$ است و سینا باید یک زیر مستطیل دلخواه با اضلاع موازی زمین اصلی انتخاب کنه.

در زمین $k$ گنج وجود داره که $i$امین در خانه $(x_i, y_i)$ است. به دلیل قانع بودن سینا، او فقط می‌خواد مستطیلی انتخاب کنه که حداقل $t$ گنج داشته باشه. به او بگویید به چند طریق این کار امکان پذیر است.

ورودی🔗

در خط اول ورودی به ترتیب چهار عدد طبیعی $n$، $m$، $k$ و $t$ با فاصله از هم آمده است. $1 \le n, m, k \le 3000$ $1 \le t \le min(10,k)$ در $k$ خط بعد ۲ عدد طبیعی $x_i$ و $y_i$ به ترتیب با فاصله از هم آمده اند. $1 \le x_i \le n$ $1 \le y_i \le m$

خروجی🔗

تعداد زیرمستطیل هایی که شامل حداقل $t$ گنج هستند را چاپ کنید.

مثال🔗

ورودی نمونه ۱🔗

2 2 1 1
1 2

خروجی نمونه ۱🔗

4

برای این مثال یک مستطیل $1 \times 1$ و یک مستطیل $2 \times 1$ و یک مستطیل $1 \times 2$ و یک مستطیل $2 \times 2$ وجود دارد که شامل گنج در مختصات 1 2 است

ورودی نمونه ۲🔗

3 2 3 3
1 1
3 1
2 2

خروجی نمونه ۲🔗

1

ورودی نمونه ۳🔗

3 2 3 2
1 1
3 1
2 2

خروجی نمونه ۳🔗

4

• محدودیت زمان: ۲ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

پارسا در شهری زیبا زندگی می‌کند و اصغر از شهر می خواهد دزدی کند.

پانورامای شهر را می‌توان به صورت یک رشته $s$ نمایش داد که هر کاراکتر نشان‌دهنده شکل ساختمان متناظر است. ساختمان‌های مختلف ممکن است شکل یکسانی داشته باشند و بنابراین در رشته با کاراکترهای یکسان نمایش داده می‌شوند. اصغر یک رشته $p$ را به عنوان برنامه دزدی خود انتخاب کرده است. خوشبختانه این رشته $p$ به دست پلیس افتاده است. حال آنها می‌خواهند تمام مجموعه ساختمان‌هایی که در خطر هستند را پیدا کنند، اما یک پیچیدگی در راه است.

به دستور شهردار جدید، برخی از ساختمان‌ها در شهر باید تخریب شوند. آنها یکی پس از دیگری و به ترتیبی که در رشته $s$ ظاهر می‌شوند، از چپ به راست، تخریب می‌شوند. این برنامه تخریب در شهر خوب شناخته شده است.

دزدی می‌تواند در هر زمانی اتفاق بیفتد: قبل از تمام تخریب‌های برنامه‌ریزی شده، بعد از آنها، یا بین تخریب هر دو ساختمانی که یکی پس از دیگری در برنامه تخریب هستند. با این حال، هیچ تخریبی نمی‌تواند در طول دزدی اتفاق بیفتد.

اصغر به طور دقیق طبق برنامه دزدی خود از چپ به راست دزدی می‌کند. او هیچ ساختمانی را به جز آنهایی که تخریب شده‌اند، نمی‌پراند. او فقط می‌تواند کل برنامه را اجرا کند. با این حال، ممکن است تعداد زیادی از مجموعه‌های ساختمان‌ها وجود داشته باشند که در خطر دزدیده شدن هستند.

به طور رسمی، در نظر بگیرید رشته $t$ که ما از $s$ با حذف کاراکترهای متناظر با ساختمان‌های تخریب شده به دست می‌آوریم. توجه داشته باشید که رشته $t$ در ابتدا برابر با $s$ است اما پس از هر تخریب تغییر می‌کند. اصغر می‌تواند یک مجموعه از ساختمان‌ها را دزدیده اگر در یک لحظه از زمان، این مجموعه یک زیررشته از $t$ را تشکیل دهد و این زیررشته برابر با رشته $p$ باشد.

وظیفه شما این است که دقیقا تعداد مجموعه‌هایی را که در خطر دزدیده شدن هستند، پیدا کنید.

ورودی🔗

خط اول ورودی شامل یک رشته غیرخالی $s$ متشکل از حروف کوچک و بزرگ انگلیسی، ارقام، کاراکترهای ', !, _, . و - است که ساختمان‌های شهر را از چپ به راست نشان می‌دهد. طول این رشته از $1,000,000$ تجاوز نمی‌کند. خط دوم ورودی شامل رشته $p$ است که برنامه دزدی اصغر را نشان می‌دهد. طول این رشته نیز از $1,000,000$ تجاوز نمی‌کند. خط سوم ورودی شامل یک عدد صحیح $m (0 \leq m \leq |s|)$ است که طول برنامه تخریب شهردار است. خط بعدی شامل یک دنباله افزایشی از اعداد صحیح $x_1, x_2, \ldots, x_m (1 \leq x_1 < \ldots < x_m \leq |s|)$ است که شاخص‌های ساختمان‌ها در ترتیبی است که باید تخریب شوند.

خروجی🔗

یک عدد صحیح که تعداد مجموعه‌های مختلف ساختمان‌ها که می‌توانند طبق برنامه اصغر دزدیده شوند.

مثال🔗

ورودی نمونه ۱🔗

aabbcc
abc
3
2 4 5

خروجی نمونه ۱🔗

2

توضیحات: پاسخ برای نمونه داده شده $2$ است زیرا دنباله‌های ممکن از ساختمان‌ها که می‌توانند دزدیده شوند عبارتند از: $135$ (پس از دو تخریب ساختمان) و $136$ (پس از تمام سه تخریب ساختمان).