+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
محمد حیدری به تازگی بعد از گذشت 14 ترم از
ورودش به رشته مهندسی کامپیوتر دانشگاه ولی عصر، فارغ التحصیل و بالاخره از
دانشگاه آزاد شده است! احتمالا نمیتوانید تصور کنید که وی چقدر از پیشرفت محیط
پیرامونش شگفتزده شدهاست. قبل از اینکه به دانشگاه برود، عدهی کمی از گوشی
هوشمند استفاده میکردند؛ اما اکنون همه گوشی هوشمند دارند و سبک زندگیها تغییر
کردهاست. در اولین روزهای اول پس از فارغ التحصیلی، یکی از دوستانش به مناسبت این
روز بزرگ، یک کد تخفیف اسنپ برایش فرستاد و وی را با اسنپ آشنا کرد.
او پس از چندین بار استفاده از اسنپ و معرفی به دوستان خود و استفاده از کد تخفیف برای سفرهای بعدی متوجه شد که *زیرالفبا* همه کدهای تخفیف یکسان است. *زیرالفبا* یک رشته برابر است با **مجموعهی** حروف متفاوت که در این رشته وجود دارند. برای مثال اگر کد تخفیف `XHx2ZLL` باشد زیرالفبای آن برابر با $\{2,H,L,X,Z,x\}$ خواهد بود.
امروز یکی از دوستان محمد به او $n$ کد تخفیف اسنپ، که آنها را با $s_1, s_2, ..., s_n$ نشان میدهیم، فرستادهاست؛ محمد میخواهد قبل از استفاده از این کدهای تخفیف مطمئن شود که این کدهای تخفیف معتبر هستند. او برای هر کد تخفیف، میخواهد زیرالفبا آن را با زیرالفبای کد تخفیف **معتبر** و استفادهشده $t$ مقایسه کند تا متوجه شود که کدامین کدهای تخفیف معتبر هستند. از آنجا که این فرایند طول خواهد کشید، شما باید برنامهای بنویسید تا مشخص کند هر کد تخفیف معتبر هست یا خیر.
# ورودی
سطر اول ورودی شامل عدد طبیعی $n$ و کد تخفیف $t$ است. سپس در $n$ سطر بعدی به ترتیب $s_1$ و $s_2$ و ... و $s_n$ آمدهاست. *تضمین میشود همه کدهای تخفیف ورودی تنها از حروف کوچک و بزرگ و ارقام انگلیسی تشکیل شدهاند.*
$$1 \le n \le 100$$
$$1 \le |s_i|, |t| \le 100$$
# خروجی
در خروجی باید $n$ سطر چاپ کنید. در سطر $i$ ام `Yes` چاپ کنید اگر کد تخفیف $i$ ام معتبر است و در غیر اینصورت `No` چاپ کنید.
# مثال
## ورودی نمونه
```
4 quera102
quEra0012
qu0erraa12
sN0Ap12
qurra00L
```
## خروجی نمونه
```
No
Yes
No
No
```
بحران فارغ التحصیلی!
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
ریحانه و پروانه ماموران سمباف (سازمان مبارزه با اساتید فراری!) هستند که تحرکات یک استاد فراری
(از دست دانشجویان) را دنبال میکنند. منابعی ناشناس آنها را از تلاش اخیر وی
برای فرار مطلع کردهاند. آنها اکنون میدانند که وی قصد دارد از ارتباطات خود
برای سوار شدن بر جت CIA در فرودگاه رفسنجان استفاده کند. اطلاعات دست اول
سمباف تایید کرده است که همه جتهای سازمان سیا در کدهای ارتباطی خود دارای رشته FBI هستند. ریحانه
و پروانه فهرستی از تمام جتهای آماده شده برای روز تعیین شده را جمع آوری کردند.
دقیقاً پنج جت در این لیست وجود دارد. برنامه ای بنویسید که تمام جت های سیا را
پیدا کند.
# ورودی
دقیقا 5 ردیف رشته به عنوان ورودی داده میشود. هر ردیف دقیقاً یک کد ارتباطی
جت سیا از لیست را نشان میدهد. کد ارتباطی حداکثر از 10 حرف انگلیسی بزرگ، اعداد
0 تا 9 و یا خط فاصله (-) تشکیل شده است.
# خروجی
تنها خط خروجی باید حاوی لیستی از اعداد صحیح باشد که شماره
ردیفهای ورودی مربوطه را که شامل کدهای ارتباطی ثبت شده جتهای سیا است، به ترتیب
افزایشی نشان میدهد.
اگر جت سیا وجود ندارد، رشته !HE GOT AWAY را خروجی بدهد.
توجه: حروف بزرگ و کوچک متفاوت در نظر گرفته می شوند،
بنابراین عبارت !He Got Away غلط
است!
# مثال
## ورودی نمونه ۱
```
A-FBI2
9A-IRKOK
RE-KGB3
I-NTERPOL
GM-MI6
```
## خروجی نمونه ۱
```
1
```
## ورودی نمونه ۲
```
N323-CIA
F5-B13I
F-BI-32
MPM-DU-CIA
HAKHFSHT
```
## خروجی نمونه ۲
```
HE GOT AWAY!
```
## ورودی نمونه ۳
```
45-FBI
BOND-007
DT-FBI14
S1N4-13
N1M4-FBILL
```
## خروجی نمونه ۳
```
1 3 5
```
ماموریت غیرممکن!
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
ریحانه، میخواهد
برای عید نوروز شیرینی مربایی به شکل مثلث بسازد. مشکل اینجاست که برای ساخت قالبهای
شیرینی فقط مقدار محدودی ورق فلزی دارد. البته ریحانه وسواس دارد و میخواهد حتما طول
اضلاع مثلثی اعداد طبیعی باشند. برنامهای بنویسید تا به ریحانه نشان دهد که با
این مقدار چند مدل شیرینی مثلثی میتواند بسازد؟
دو قاب شیرینی
مثلثی متفاوت در نظر گرفته میشوند اگر مجموعهی طول اضلاع آنها با یکدیگر متفاوت
باشند. (به مثالها و شکلهایشان توجه کنید!)
# ورودی
در تنها سطر ورودی عدد طبیعی $n$ آمده است که طول ورق اولیه را نشان میدهد.
$$ 3 \le n \le 1\ 000\ 000 $$
# خروجی
در تنها سطر خروجی باید تعداد قالبهایی که ریحانه میتواند بسازد چاپ شود.
# مثال
## ورودی نمونه ۱
```
5
```
## خروجی نمونه ۱
```
1
```
## ورودی نمونه ۲
```
12
```
## خروجی نمونه ۲
```
3
```
توضیح مثال ۲:
مهدی با چوبی به طول ۱۲، قاب عکسهایی به شکلهای زیر میتواند بسازد.
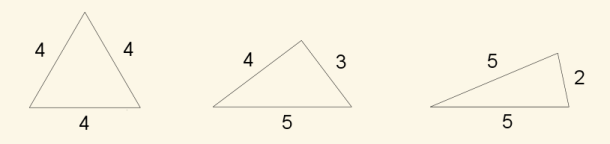
شیرینی مثلثی
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
مهدی به شدت به پادکست علاقه دارد. وی روزانه پادکستهای مختلفی (به ویژه پادکام، پادکست اختصاصی انجمن مهندسی کامپیوتر دانشگاه ولی عصر) را گوش میکند و کلمات کلیدی
آنها را یادداشت مینماید. حال میخواهد این کلمات را به هم بچسباند و در یک فایل
ذخیره کند. به دلیل این که این پادکست برای او بسیار مهم است، وی میخواهد مکان
فایل در پوشهای که آن را ذخیره میکند در بالاترین جای ممکن باشد. نحوه جایگیری
فایل ها در کامپیوتر او به صورت الفبایی است. برای همین او میخواهد که رشتهی
نهایی به صورت الفبایی کوچکترین حالت ممکن را داشته باشد.
اگر $s$ و $t$ دو رشته از حروف باشند، که تعداد حروفشان یکسان است و $s_i$ حرف iام رشتهی s , $t_j$ حرف $j$م رشتهی $t$ را نشان دهد، آنگاه گوییم $s$ از $t$ به صورت الفبایی کوچکتر است اگر برای یک $i$ داشته باشیم $s_i < t_i$
و برای تمام $k < i$ داشته باشیم $s_k = t_k$.
# ورودی
در سطر اول ورودی $n$ آمده است که نشاندهندهی تعداد کلمات است.
در $n$ خط بعدی در هر خط یک کلمه آمده است. طول رشتهی $i$ برابر $l_i$ است. هر رشته از حروف کوچک انگلیسی تشکیل شدهاست.
$$ 1 \le n \le 100 $$
$$ 1 \le l_i \le 20 $$
# خروجی
خروجی شامل یک رشته است که نشاندهندهی رشته قابل ساختی است که از نظر الفبایی کمینه است.
# مثال
## ورودی نمونه ۱
```
3
c
a
b
```
## خروجی نمونه ۱
```
abc
```
محمدجواد با چسباندن کلمه ها به هم میتواند این ۶ رشته را بسازد: {$cba$ ,$cab$ ,$bca$ ,$bac$ ,$acb$ ,$abc$} که از بین آنها رشته $abc$ از بقیه از نظر الفبایی کوچکتر است.
## ورودی نمونه ۲
```
7
bat
javo
he
on
aaghe
irshi
bek
```
## خروجی نمونه ۲
```
aaghebatbekheirshijavoon
```
مهدی و پادکام!
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
دانشجویان به مناسبت روز استاد برای دکتر صباغ یک ساعت شنی هدیه خریدهاند. حال، این ساعت شنی را داریم که اگر همهی شنهای داخل آن کاملاً در سمت بالا باشد، $M$ دقیقه طول میکشد تا شنها به قسمت پایین منتقل شوند. ما این ساعت شنی را در لحظهی ۰ روی میز قرار دادیم و راس دقیقهی $T$ این ساعت شنی را روی میز بر میداریم. در لحظهی ۰ همهی شنها در قسمت بالایی ساعت قرار دارد.

همچنین $n$ لحظه $t_1, t_2, \dots, t_n\,$ از قبل به ما داده شده و میتوانیم در این لحظهها ساعت شنی را برعکس کنیم، یا هیچ تغییری ندهیم. (در بقیه لحظهها این کار ممکن نیست.) میخواهیم طوری این فرآیند را انجام دهیم که هیچ یک دقیقهی متوالی در این $T$ دقیقه پیش نیاید که ساعت شنی روی میز باشد و همهی شنهایش به قسمت پایین رفته باشد و حرکتی نکند (توجه کنید یک لحظه خالی شدن مهم نیست). از شما میخواهیم برنامهای بنویسید که بررسی کند آیا میتوانیم این کار را انجام دهیم یا خیر؟
برای بهتر متوجه شدن سوال، به توضیح نمونهها توجه کنید.
# ورودی
در سطر اول ورودی، عدد صحیح $t$ آمده که تعداد تستهای یک ورودی را نشان میدهد.
$$1 \leq t \leq 100$$
در سطر اول هر تست سه عدد صحیح $n$، $M$ و $T$ با فاصله از هم داده میشوند.
$$1 \leq n, M \leq 100$$
$$1 \leq T \leq 300$$
در سطر دوم هر تست $n$ عدد صحیح $t_1, t_2, \dots, t_n\,$ داده میشود.
$$0 \lt t_1 \lt t_2 \lt \dots \lt t_n \lt T$$
# خروجی
برای هر تست، در صورتی که این کار شدنی است `YES` و در غیر این صورت `NO` چاپ کنید.
# مثالها
## ورودی نمونه ۱
```
2
2 6 10
3 6
1 10 25
11
````
## خروجی نمونه ۱
```
YES
NO
````
<details>
<summary>
**توضیح نمونه ۱**
</summary>
در تست اول، $M = 6$ دقیقه طول میکشد تا ساعت شنی کاملاً خالی شود. ساعت شنی را در دقیقهی ۰ روی میز قرار میدهیم و در دقیقهی $T = 10$ از روی میز بر میداریم. در دقیقههای $t_1 = 3$ و $t_2 = 6$ میتوانیم ساعت شنی را برعکس کنیم.
اگر در لحظهی $t_2 = 6$ برعکس کنیم هیچ وقت ساعت یک دقیقه متوالی بیحرکت نخواهد بود. چون از دقیقهی ۰ تا ۶ در حال خالی شدن است و درست در همان لحظه، ساعت برعکس میشود و در دقیقهی ۱۰، هنوز به اندازهی ۲ دقیقه شن دارد و هیچوقت ساعت از حرکت نیفتاده است.
در تست اول، $M = 10$ دقیقه طول میکشد تا ساعت شنی کاملاً خالی شود. ساعت شنی را در دقیقهی ۰ روی میز قرار میدهیم و در دقیقهی $T = 25$ از روی میز بر میداریم. در دقیقهی $t_1 = 11$ میتوانیم ساعت شنی را برعکس کنیم.
قبل از رسیدن به اولین زمان ممکن برای تغییر وضعیت ساعت، در بازهی دقیقهی ۱۰ تا ۱۱ ساعت شنی بیحرکت میماند. پس نمیتوانیم به هدفمان برسیم.
</details>
هدیه به دکتر صباغ!
* محدودیت زمان: ۱ ثانیه
* محدودیت حافظه: ۲۵۶ مگابایت
------------------------------
پروانه به شدت از دست بادکنک فروشی محل عصبانی است! وی قصد دارد تا برای درآوردن حرص طرف، بادکنکهای حاضر در بیرون مغازهاش را بترکاند! رنگ بادکنک $ i $ام $a_i$ است. پروانه در ابتدای هر روز همزمان بادکنکهای هر دسته از بادکنکهای پشت سر هم و هم رنگ که شامل حداقل ۳ بادکنک باشد میترکاند و در پایان هر روز بادکنکهای باقیمانده دوباره در یک ردیفِ پیوسته با همان ترتیب قرار میگیرند. میخواهیم بدانیم هر بادکنک در چه روزی میترکد.
# ورودی
در خط اول ورودی عدد $ n $ آمده است که تعداد بادکنکها را نشان میدهد.
$$1 \le n \le 300\ 000$$
$$1 \le a_i \le 10^9$$
# خروجی
به ازای هر بادکنک روز ترکیدنش را چاپ کنید، اگر یک بادکنک هیچگاه نمیترکد `-1` را چاپ کنید.
# مثال
## ورودی نمونه
```
7
1 2 2 3 3 3 2
```
## خروجی نمونه
```
-1 2 2 1 1 1 2
```
## ورودی نمونه
```
20
2 2 2 1 1 2 2 1 2 1 2 1 1 2 2 2 1 2 2 2
```
## خروجی نمونه
```
1 1 1 -1 -1 -1 -1 -1 -1 -1 -1 2 2 1 1 1 2 1 1 1
```
خشم پروانه!
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
ایلان ماسک بعد از شکست در خرید توییتر وارد بازار کشت و فروش شلغم شد! امّا در این بین، علفهای هرز مانع کسب و کار او شدند. برای همین، شروع به حذف کردن علفهای هرز کرده است و از شما کمک میخواهد.
مزرعهٔ او به شکل جدولی $n\times m$ است که دارای $n$ سطر با شمارههای $0$ تا $n - 1$ از بالا به پایین و $m$ ستون با شمارههای $0$ تا $m - 1$ از چپ به راست میباشد. در ابتدا $k$ علف هرز در مزرعه وجود دارد. او در هر مرحله میتواند یکی از عملیاتهای زیر را انجام دهد:
+ یک علف هرز از خانهٔ $(i, j)$ را با دست بکَنَد. در این صورت $w_{i, j}$ انرژی مصرف میکند. (برای خم شدن و کندن علف هرز)
+ پا روی خانهٔ $(i, j)$ بگذارد، در این صورت یکی از علفهای هرز موجود در آن خانه از بین رفته و یک علف هرز به خانهی $((i + 1)\mod n, j)$ و علف هرزی دیگر به خانهی $(i, (j + 1)\mod m)$ اضافه میشود. توجه کنید که در این عملیات هیچ انرژیای از او کم نمیشود ($a\mod b$ برابر با باقی مانده تقسیم $a$ بر $b$ است).
حال او وضعیت اولیهٔ مزرعه و علفهای هرز را به شما میدهد و از شما میخواهد که کمترین انرژی لازم برای از بین بردن تمامی علفهای هرز مزرعه را محاسبه کنید.
# ورودی
در خط اول دو عدد $n$ و $m$ و $k$ داده میشود.
در هر یک از $n$ سطر بعدی $m$ عدد آمده است که عدد $j$ ام در سطر $i$ ام مقدار $w_{i, j}$ را مشخص میکند.
در خط $i$ ام از $k$ خط بعدی دو عدد $x_i$ و $y_i$ آمده که نشان میدهد علف هرز $i$ ام در خانه $(x_i, y_i)$ است.
$$ 1 \le n, m \le 1\ 000 $$
$$1 \le k \le 1\ 000$$
$$ 0 \le x_i < n $$
$$ 0 \le y_j < m $$
$$ 1 \le w_{i, j} \le 1\ 000$$
**دقت کنید ممکن است در ابتدا در یک خانه بیش از یک علف هرز وجود داشته باشد.**
# خروجی
در یک خط عدد خواسته شده را چاپ کنید.
# مثال
## ورودی نمونه ۱
```
2 2 1
3 1
1 1
0 0
```
## خروجی نمونه ۱
```
2
```
در ابتدا یک علف هرز در خانهٔ $(0 ,0)$ وجود دارد. ایلان روی آن پا گذاشته و در نتیجه در هر یک از خانههای $(1 ,0)$ و $(0 ,1)$ یک علف هرز بوجود میآید. سپس هر کدام از علفهای هرز جدید را با دست میکند و در مجموع ۲ واحد انرژی از دست میدهد.
## ورودی نمونه ۲
```
3 3 2
7 5 1
4 3 1
1 2 1
0 1
1 0
```
## خروجی نمونه ۲
```
8
```
در ابتدا دو علف هرز یکی در خانه $(0,1)$ و دیگری در خانه $(1,0)$ موجود است، ایلان با پا گذاشتن روی این دو علف آنها را به صورت $(0,2)$، $(1,1)$، $(1,1)$ و $(2,0)$ درمیآورد (توجه کنید دو علف هرز در خانه $(1,1)$ موجود است) سپس تمامی آنها را با دست میکند که در مجموع از او ۸ واحد انرژی میگیرد همچنین میتوان ثابت کرد این مقدار کمینه انرژی لازم است.
ایلان ماسک و بیزنس جدید!
+ محدودیت زمان: ۲ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
در دوران صدارت دکتر شهریور دانشجویان به شدت به عدد 28 اعتقاد داشتند تا جاییکه یک دوره کامل را به اسم این عدد دوره 1028یا گذاشته بودند. آنها **دوره ۱۰۲۸ ایا**، **دوره ۲۸ ایا** را بسیار خفن میپنداشتند(زیرا **دوره ۲۸ ایا** واقعا خفن بودند). اعتقاد **دوره ۱۰۲۸ ایا** به خفونت **دوره ۲۸ ایا** چنان بود که فکر میکردند **دوره ۲۸ ایا** میتوانستند حتی مساله توقف را حل کنند!
مساله توقف ( به انگلیسی : Halting problem ) مطرح می کند که آیا می توان برنامه ای نوشت که یک برنامه از ورودی بگیرد و تعیین کند که آیا برنامه متوقف می شود یا خیر. ثابت شده که در حالت کلی، الگوریتمی برای حل این مساله وجود ندارد.
مسئول **دوره ۱۰۲۸ ایا** برای اینکه اعتماد به نفس **دوره ۱۰۲۸ ایا** تقویت شود، نسخه ساده شدهای از مساله هالت را به آنها داد تا آنها فکر کنند مثل **دوره ۲۸ ایا** خفن هستند.
در این نسخه ساده شده سه نوع دستور موجود است:
```
assign a = b + c
cout a
goto l
```
که در آن $a$ و $b$ و $c$ یک **حرف کوچک انگلیسی** (که نام یک متغیر است) یا یک **عدد یک رقمی** هستند و $l$ شماره خطی از برنامه است. تضمین میشود که بعد از `assign` متغیر `a` همیشه یک حرف کوچک انگلیسی است.
شما باید خط به خط برنامه را دنبال کنید، در صورتی که برنامه پایانناپذیر است، $-1$ را چاپ کنید. در غیر اینصورت خروجی این برنامه را چاپ کنید. در این برنامه `cout` به معنای چاپ کردن یک عدد یا یک متغیر است. `goto` به معنای پرش به یک خط خاص است (خطها از ۱ شمارهگذاری شدهاند). `assign a = b + c` یعنی $b+c$ را در متغیر $a$ قرار بده. هر حرف کوچک انگلیسی نشاندهنده یک متغیر است و محتوای همه متغیرها در ابتدا صفر میباشد.
با توجه به اینکه جواب مسئله ممکن است بزرگ شود شما باید **باقی مانده خروجی بر $10^9+7$** را بگویید.
# ورودی
در ورودی یک برنامه به شما داده میشود.
در خط اول $n$ تعداد خطهای برنامه و در $n$ خط بعد در هر خط یک دستور از برنامه داده میشود.
$$1 \le l \le n \le 100\ 000$$
# خروجی
اگر برنامه دادهشده تمام نمیشود، در تنها سطر خروجی $-1$ چاپ کنید.
در غیر اینصورت خروجیهای برنامه (به ازای هر `cout`) را چاپ کنید.
# مثال
## ورودی نمونه ۱
```
2
assign a = 2 + 2
cout a
```
## خروجی نمونه ۱
```
4
```
## ورودی نمونه ۲
```
4
assign a = 1 + 0
cout a
assign a = a + a
goto 2
```
## خروجی نمونه ۲
```
-1
```
## ورودی نمونه ۳
```
7
cout 0
goto 5
cout 1
goto 7
cout 2
goto 3
cout 3
```
## خروجی نمونه ۳
```
0
2
1
3
```
مسئله دکتر شهریور
+ محدودیت زمان: ۲.۵ ثانیه
+ محدودیت حافظه: ۱۰۲۴ مگابایت
----------
پارسا چون خیلی بچه درس خونی است و به شدت به حل معماها علاقه دارد، سر کلاس اصلا حواسش به درس نبود و در حل معما فرو رفته بود. به همین خاطر، یادش رفت تمرین های فیزیکش را انجام دهد. او هم اکنون در سر کلاس فیزیکش است و چیزی از مساحت زیر نمودار نمی داند.
دکتر شریفی (معلم فیزیک پارسا) که از موضوع خبر دارد، برای تنبیه پارسا، هر ثانیه از $q$ ثانیه زنگ کلاس، یکی از دو کار زیر را انجام می دهد :
1. یک خط با عرض از مبدا $b_i$ و شیب $a_i$ روی تخته می کشد.
2. از پارسا می خواهد مساحت زیر نمودار $L_i$ تا $R_i$ را حساب کند.
**در واقع شما در هر $x$، ارتفاع نمودار در آن $x$ را برابر ماکسیمم $y$ خطوط در آن $x$ فرض کنید.**
پارسا که چیزی از این ها بلد نیست، از شما (کناردستیاش) می خواهد به سرعت پاسخ ها را برای اون محاسبه کنید.
برای وضوح بیشتر به مثال ۲ مراجعه کنید.
# ورودی
در خط اول ورودی، عدد $q$، تعداد ثانیه های زنگ کلاس فیزیک می آید.
در ادامه $q$ خط می آیند. خط $i$ ام، به یکی از دو صورت زیر است :
$$1 \ a_i \ b_i$$
$$2 \ L_i \ R_i$$
که حالت اول نشان دهنده اضافه کردن خط توسط دکتر شریفی است و حالت دوم نشان دهنده یک پرسش از پارسا است.
$$1 \leq q \leq 100\ 000$$
$$-10\ 000 \leq a_i, b_i \leq 10\ 000$$
$$0 \leq L_i < R_i \leq 20\ 000\ 000$$
# خروجی
به ازای هر پرسش از پارسا، در یک خط، مساحت زیر نمودار را چاپ کنید. اختلاف مطلق و نسبی شما با جواب درست نباید بیش از $10^{-6}$ باشد. در واقع اگر جواب شما $p$ و جواب درست $j$ باشد، در صورتی جواب شما درست در نظر گرفته میشود که
$\frac{|p - j|}{max(j, 1)} \le 10^{-6}$.
# مثال
## ورودی نمونه ۱
```
2
1 1 0
2 0 1
```
## خروجی نمونه ۱
```
0.500000
```
دقت کنید که $L , R$ گفته شده به حالت بسته - باز بر روی محور $x$ هاست.
در نتیجه بازه $[0 , 1)$ ، شامل یک مثلث قائمه الزاویه به اضلاع قائمه $1$ خواهد بود که مساحت آن $0.5$ است.
همچنین دقت کنید ممکن است این مقدار منفی هم باشد (در صورتی که تمام خط ها زیر محور $x$ ها بروند)
همچنین اگر خطی کشیده نشده بود، مساحت زیر نمودار را ۰ در نظر بگیرید.
## ورودی نمونه ۲
```
6
1 -1 2
2 0 1
1 0 1
2 0 2
1 1 -1
2 0 3
```
## خروجی نمونه ۲
```
1.500000
2.500000
4.000000
```
پارسا و دکتر شریفی!
+ محدودیت زمان: ۴ ثانیه
+ محدودیت حافظه: ۱۰۲۴ مگابایت
----------
حسین ADHD شدید دارد و به همین خاطر دکتر به وی گفته تا به شهرهای مختلف سفر
کند تا انرژی وی تخلیه شود. علاوه بر این، حسین هیستری جمعی دارد و به همین خاطر
فقط میتواند از یک الگوی خاص در انتخاب مسیر خود پیروی کند. به حسین کمک کنید تا
تمام زیر مجموعههایی که در مسیر مسافرتهای وی وجود دارند و از الگوی حسین پیروی
میکنند را پیدا کند.
یک گراف اصلی و یک گراف الگو به شما داده میشود. حال شما میبایست تعداد زیر گرافهای موجود در گراف اصلی را پیدا کنید به طوری که این زیرگرافها مشابه گراف الگو باشند. (برای فهم بهتر مسئله به شکلهای پایین صفحه مراجعه کنید)
### نکات مهم:
1. گرافها رنگی و جهتدار هستند.
2. گراف الگو ضعیفا همبند است. (در صورتی که جهت یالها را در نظر نگیریم، گراف ما همبند است)
3. بین هر دو راس گراف الگو حداکثر یک یال در هر جهت وجود دارد.
4. هر راس گراف شامل یک شناسه یکتا و یک رنگ است.
5. هر یال گراف شامل یک شناسه راس مبدا و یک شناسه راس مقصد است.
توجه کنید که سوال راهحل کامل ندارد و تستها به صورت رندوم ساخته شدند و برنامه شما هر چه بهتر باشد میتواند نمره بهتری دریافت کند.
# ورودی
### اطلاعات گراف اصلی
1. در خط اول ورودی $n_1$ (تعداد راسهای گراف اصلی) وارد میشود.
2. سپس در $n_1$ خط بعدی یک رشته (شناسه راس) و $a_i$ (شماره رنگ راس) برای راسهای گراف اصلی با یک فاصله از هم وارد میشوند.
3. سپس مقدار $m_1$ (تعداد یالهای گراف اصلی) وارد میشود.
4. سپس در $m_1$ خط بعدی دو رشته برای شناسهی راس مبدا و شناسهی راس مقصد یالهای گراف اصلی با یک فاصله از هم وارد میشوند.
### اطلاعات گراف الگو
5. در خط بعد $n_2$ (تعداد راسهای گراف الگو) وارد میشود.
6. سپس در $n_2$ خط بعدی یک رشته (شناسه راس) و $b_i$ (شماره رنگ راس) برای راسهای گراف الگو با یک فاصله از هم وارد میشوند.
7. سپس مقدار $m_2$ (تعداد یالهای گراف الگو) وارد میشود.
8. سپس در $m_2$ خط بعدی دو رشتهی شناسهی راس مبدا و شناسهی راس مقصد یالهای گراف الگو با یک فاصله از هم وارد میشوند.
$$1 \le n_1 \le 30\ 000$$
$$1 \le a_i \le 4$$
$$1 \le m_1 \le 10*n_1$$
$$1 \le n_2 \le 5$$
$$1 \le b_i \le 4$$
$$1 \le m_2 \le 20$$
# خروجی
خروجی تنها شامل یک عدد است که تعداد زیرگرافهای موجود از گراف اصلی (شبیه به گراف الگو) را نشان میدهد.
# مثال
## ورودی نمونه ۱
```
5
1 1
2 2
3 2
4 2
5 2
8
1 2
1 5
2 3
2 4
2 5
3 4
5 3
5 4
3
A 1
B 2
C 2
2
A B
B C
```
## خروجی نمونه ۱
```
5
```
<details>
<summary>توضیحات نمونهی ۱</summary>
گراف اصلی نمونه ۱:
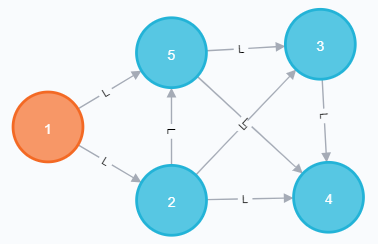
گراف الگو نمونه ۱:
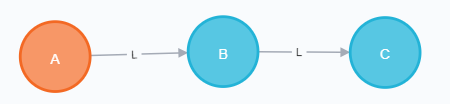
با توجه به جدول زیر تعداد زیرگرافهای مشابه گراف الگو در گراف اصلی، ۵ تاست، بنابراین عدد ۵ در خروجی چاپ میشود.
| |راس A|راس B|راس C|
|:-------:|:---:|:---:|:---:|
|زیرگراف ۱|راس ۱|راس ۲|راس ۳|
|زیرگراف ۲|راس ۱|راس ۲|راس ۴|
|زیرگراف ۳|راس ۱|راس ۲|راس ۵|
|زیرگراف ۴|راس ۱|راس ۵|راس ۳|
|زیرگراف ۵|راس ۱|راس ۵|راس ۴|
</details>
## ورودی نمونه ۲
```
5
1 1
2 2
3 2
4 2
5 2
4
1 2
1 3
1 4
1 5
3
A 1
B 2
C 2
2
A B
A C
```
## خروجی نمونه ۲
```
12
```
<details>
<summary>توضیحات نمونهی ۲</summary>
گراف اصلی نمونه ۲:
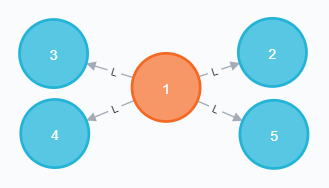
گراف الگو نمونه ۲:
با توجه به جدول زیر تعداد زیرگرافهای مشابه گراف الگو در گراف اصلی، ۱۲ تاست، بنابراین عدد ۱۲ در خروجی چاپ میشود.
| |راس A|راس B|راس C|
|:--------:|:---:|:---:|:---:|
|زیرگراف ۱ |راس ۱|راس ۲|راس ۳|
|زیرگراف ۲ |راس ۱|راس ۲|راس ۴|
|زیرگراف ۳ |راس ۱|راس ۲|راس ۵|
|زیرگراف ۴ |راس ۱|راس ۳|راس ۲|
|زیرگراف ۵ |راس ۱|راس ۳|راس ۴|
|زیرگراف ۶ |راس ۱|راس ۳|راس ۵|
|زیرگراف ۷ |راس ۱|راس ۴|راس ۲|
|زیرگراف ۸ |راس ۱|راس ۴|راس ۳|
|زیرگراف ۹ |راس ۱|راس ۴|راس ۵|
|زیرگراف ۱۰|راس ۱|راس ۵|راس ۲|
|زیرگراف ۱۱|راس ۱|راس ۵|راس ۳|
|زیرگراف ۱۲|راس ۱|راس ۵|راس ۴|
</details>
## ورودی نمونه ۳
```
2
1 1
2 1
2
1 2
2 1
2
A 1
B 1
1
A B
```
## خروجی نمونه ۳
```
2
```
<details>
<summary>توضیحات نمونهی ۳</summary>
گراف اصلی نمونه ۳:

گراف الگو نمونه ۳:

با توجه به جدول زیر تعداد زیرگرافهای مشابه گراف الگو در گراف اصلی، ۲ تاست، بنابراین عدد ۲ در خروجی چاپ میشود.
| |راس A|راس B|
|:-------:|:---:|:---:|
|زیرگراف ۱|راس ۱|راس ۲|
|زیرگراف ۲|راس ۲|راس ۱|
</details>