+ محدودیت زمان: ۱ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- امین و مهدی عاشق هندوانه و خربزه هستند. آن‌ها $h$ هندوانه و $k$ خربزه از میوه فروشی خریده‌اند. می‌دانیم هندوانه‌ها و خربزه‌ها هم وزن و یکسان هستند. امین و مهدی بر این عقیده‌اند که خوردن هر هندوانه ۲ دقیقه بر عمر اضافه می‌کند. همچنین خوردن هر خریزه ۱ دقیقه بر عمر اضافه می‌کند. آن‌ها می‌خواهند این $h + k$ میوه را طوری بین خودشان تقسیم کنند که مجموع عمر اضافه شده‌ی آن‌ها برابر باشد. آن‌ها هیچ‌وقت یک هندوانه یا خریزه را نصف نمی‌کنند و این کار را بی احترامی به آن میوه می‌دانند! از شما می‌خواهیم بررسی کنید که بررسی کند آیا این کار شدنی است یا نه؟ # ورودی در سطر اول ورودی، عدد صحیح و نامنفی $h$ داده می‌شود. در سطر دوم ورودی، عدد صحیح و نامنفی $k$ داده می‌شود. $$0 \leq h, k \leq 100$$ # خروجی در تنها سطر خروجی، در صورتی که این تقسیم شدنی است رشته‌ی `YES` و در غیر این صورت رشته‌ی `NO` را چاپ کنید. # مثال‌ها ## ورودی نمونه ۱ ``` 2 4 ```` ## خروجی نمونه ۱ ``` YES ```` اگر امین و مهدی هر کدام ۱ هندوانه و ۲ خربزه بردارند به عمر هر دو نفر ۴ دقیقه اضافه می‌شود، پس پاسخ `YES` است. ## ورودی نمونه ۲ ``` 3 1 ```` ## خروجی نمونه ۲ ``` NO ```` هر طوری که این خربزه و هنداونه‌ها را بین امین و مهدی پخش کنید، مجموع دقایقی که به عمر آن‌ها اضافه می‌شود برابر نیست. بنابراین پاسخ `NO`‌است. ## ورودی نمونه ۳ ``` 0 0 ```` ## خروجی نمونه ۳ ``` YES ```` در این حالت عمر هر دو نفر ۰ دقیقه اضافه می‌شود و پاسخ `YES` می‌شود.

+ محدودیت زمان: ۱ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- یک ربات ماشینی روی مبدا مختصات صفحه‌ی مختصات دو بعدی قرار دارد. جهت این ماشین رو به $+\infty$ محور $x$ها است. برای اینکه این ربات روی صفحه حرکت کند باید به آن *فرمان* بدهیم. هر فرمان دو حالت زیر را دارد: + فرمان `Forward`، یعنی یک واحد به جلو برو. + فرمان `Rotate`، یعنی ۹۰ درجه در خلاف جهت عقربه‌های ساعت در همان نقطه بچرخ. قبل از حرکت ربات می‌توان به آن یک رشته از $n$ فرمان داد و سپس این ربات به ترتیب این فرمان‌ها را از چپ به راست هر کدام را یکبار اجرا می‌کند. امین که می‌خواهد مسیر حرکت ربات را مشخص کند. او یک مسیر را با دنباله‌ای از حرکت‌های `L`، `R`، `U` و `D` مشخص می‌کند که به ترتیب یعنی یک واحد به چپ (یا رفتن یک واحد به سمت $x$ کمتر)، راست (یک واحد $x$ بیشتر)، بالا (یک واحد $y$ بیشتر) و پایین (یک واحد $y$ کمتر) حرکت کن. حال مسئله این است که اگر رشته‌ی از $n$ کاراکتر که مسیر حرکت را به فرمتی که امین ارائه می‌دهد به شما بدهند می‌توانید آن را به فرمتی که ربات حرکت می‌کند تبدیل کنید به طوری که دقیقاً همان مسیر مورد نظر امین طی شود و کمترین تعداد عملیات انجام شود؟ # ورودی در سطر اول ورودی، عدد صحیح و مثبت $n$ آمده که تعداد کاراکترهای رشته‌ی نشان دهنده‌ی مسیر مورد نظر امین را نشان می‌دهد. $$1 \leq n \leq 100$$ در سطر دوم ورودی، یک رشته از $n$ کاراکتر `L`، `R`، `U` و `D` داده می‌شود که به ترتیب مسیر حرکت مورد نظر امین را نشان می‌دهد. # خروجی در سطر تنها سطر خروجی، یک رشته از حروف `F` و `R` چاپ کنید که نشان دهنده‌ی دنباله‌ی فرمان‌هایی است که به ربات داده می‌شود (منظور از `F` فرمان `Forward` و منظور از `R` فرمان `Rotate` است). # مثال‌ها ## ورودی نمونه ۱ ``` 10 RRRUULDDDD ```` ## خروجی نمونه ۱ ``` FFFRFFRFRFFFF ```` ## ورودی نمونه ۲ ``` 4 UDRL ```` ## خروجی نمونه ۲ ``` RFRRFRFRRF ```` ## ورودی نمونه ۳ ``` 16 URDLLURDDLURRDLU ```` ## خروجی نمونه ۳ ``` RFRRRFRRRFRRRFFRRRFRRRFRRRFFRRRFRRRFRRRFFRRRFRRRFRRRF ````

+ محدودیت زمان: ۱ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- امین و مهدی دارند یک بازی معروف را بازی می‌کنند. این بازی به این شکل است: یک شبکه $n \times n$ از نقاط روی یک برگ کاغذ کشیده می‌شود. سپس بازیکنان به نوبت دو نقطه مجاور را به هم متصل می‌کنند (از نظر افقی یا عمودی). در هر «حرکت» یک بازیکن می‌تواند یک خط بکشد که دو نقطه را به هم وصل کند. هر زمان که یک بازیکن موفق به بستن یک مربع $1 \times 1$ از نقاط می‌شود (یعنی، به واقعیت ۴ نقطه را با دقیقاً ۴ خط وصل می‌کند)، آن بازیکن مربع را «برنده» می‌شود و اولین حرف از نامش (`A` یا `B`) را در فضای خالی درون مربع می‌نویسد. در شرایط عادی، هر بازیکن تلاش می‌کند تا از این مربع‌ها به حد امکان استفاده کند (این بازی باعث خراب شدن دوستی‌های زیادی شده است). امین و مهدی دارند این بازی را بازی می‌کنند اما هر دو خجالتی‌اند و نمی‌خواهند که امتیازی را در برابر هم بگیرند. علاوه بر این، آن‌ها نمی‌خواهند دوستی‌شان را به خاطر یک بازی خراب کنند. امین و مهدی **سعی نمی‌کنند برنده شوند**، آن‌ها فقط می‌خواهند ادامه دادن بازی را و دوستی‌شان **تا زمان امکان‌پذیر** برای ادامه بازی لذت ببرند. با توجه به تنظیمات بازی که تا الان به آن رسیده‌اند، به آن‌ها کمک کنید تا **تعداد حرکاتی که می‌توانند انجام دهند بدون ایجاد هیچ مربع $1 \times 1$ از نقاط** را محاسبه کنند. # ورودی در سطر اول ورودی، عدد صحیح $n$، اندازه شبکه، آمده است. $$2 \leq n \leq 80$$ سپس یک نسخه از کاراکترهای نقشه بازی آمده است. نقشه به این شکل است که شما یک ماتریس $(2n-1) \times (2n-1)$ از کاراکترها را به ترتیب ردیف-به-ردیف دریافت می‌کنید. هر سلول می‌تواند از چهار نوع ممکن باشد ($1 \leq i, j \leq n$): + سلول در $(2i - 1, 2j - 1)$ علامت `*` دارد که نقطه $(i, j)$ را نشان می‌دهد. + سلول در $(2i, 2j)$ علامت `.` دارد که فضای خالی را نشان می‌دهد. + سلول در $(2i, 2j - 1)$ علامت `|` دارد اگر نقاط $(i, j)$ و $(i + 1, j)$ با یک خط متصل شده‌اند و علامت . در غیر این صورت است. + سلول در $(2i - 1, 2j)$ علامت `-` دارد اگر نقاط $(i, j)$ و $(i, j + 1)$ با یک خط متصل شده‌اند و علامت . در غیر این صورت است. تضمین می‌شود که هیچ بازیکنی امتیاز نگرفته است: هیچ مربع‌های واحدی هنوز تشکیل نشده‌اند. # خروجی تعداد حرکاتی را که می‌توان انجام داد، در بدترین حالت، قبل از این که امین یا مهدی مطمئن شوند که امتیازی را گرفته‌اند، خروجی دهید. # مثال‌ها ## ورودی نمونه ۱ ``` 3 *-*.* |.|.| *.*-* |...| *.*.* ```` ## خروجی نمونه ۱ ``` 2 ```` ## ورودی نمونه ۲ ``` 2 *.* ... *.* ```` ## خروجی نمونه ۲ ``` 3 ```` ## ورودی نمونه ۳ ``` 4 *-*-*.* |...|.. *-*-*-* |.....| *.*.*-* |.....| *-*-*-* ```` ## خروجی نمونه ۳ ``` 4 ````

+ محدودیت زمان: ۱ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- رشته‌ی $s_n$ به صورت بازگشتی تعریف می‌شود. $s_0$ برابر رشته‌ی `sefr` است. رشته‌ی $s_n$ از بهم چسبیدن $s_{n-1}$ و تلفظ فینگلیش سه‌رقم سمت راست طول رشته‌ی $s_{n-1}$ بدست می‌آید. بنابراین چون $s_0$‌ یک رشته‌ی چهار کاراکتری است، $s_1$ برابر `sefrchahaar` است و چون $s_1$ یک رشته‌ی یازده کاراکتری است، $s_2$ برابر `sefrchahaaryaazdah` است و... . تلفظ فینگلیش را از جدول‌های پایین سوال زیر درنظر بگیریم، توجه کنید که گاهی در تلفظ برخی از اعداد از `o` استفاده می‌کنیم؛ مثلاً وقتی می‌گوییم صد و بیست، فینگلیش‌ش می‌شود `sadobist`. | اعداد تک رقمی | تلفظ | |:---:|:---:| | `0` | `sefr` | | `1` | `yek` | | `2` | `do` | | `3` | `se` | | `4` | `chahaar` | | `5` | `panj` | | `6` | `shesh` | | `7` | `haft` | | `8` | `hasht` | | `9` | `noh` | | اعداد دو رقمی | تلفظ | |:---:|:---:| | `10` | `dah` | | `11` | `yaazdah` | | `12` | `davaazdah` | | `13` | `sizdah` | | `14` | `chahaardah` | | `15` | `paanzdah` | | `16` | `shaanzdah` | | `17` | `hifdah` | | `18` | `hijdah` | | `19` | `noozdah` | | دهگان | تلفظ | |:---:|:---:| | `10` | `dah` | | `20` | `bist` | | `30` | `si` | | `40` | `chehel` | | `50` | `panjaah` | | `60` | `shast` | | `70` | `haftaad` | | `80` | `hashtaad` | | `90` | `navad` | | صدگان | تلفظ | |:---:|:---:| | `100` | `sad` | | `200` | `devist` | | `300` | `sisad` | | `400` | `chahaarsad` | | `500` | `paansad` | | `600` | `sheshsad` | | `700` | `haftsad` | | `800` | `hashtsad` | | `900` | `nohsad` | # ورودی در سطر اول ورودی، عدد صحیح و نامنفی $n$ داده می‌شود. $$0 \leq n \leq 999$$ # خروجی در تنها سطر خروجی، رشته‌ی $s_n$ را چاپ کنید. # مثال‌ها ## ورودی نمونه ۱ ``` 2 ```` ## خروجی نمونه ۱ ``` sefrchahaaryaazdah ```` ## ورودی نمونه ۲ ``` 5 ```` ## خروجی نمونه ۲ ``` sefrchahaaryaazdahhijdahbistochahaarsioshesh ````

+ محدودیت زمان: ۱ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- امین یک مسابقه تصادفی برگزار می‌کند. در این مسابقه او یک بازه‌ی $[L, R]$ به شرکت‌کننده‌ی مسابقه می‌دهد. سپس از او می‌خواهد که یک عدد صحیح به تصادف و با احتمال برابر از این بازه انتخاب کند. اگر شرکت‌کننده عدد $k$ را انتخاب کند، به او به اندازه‌ی تعداد مقسوم‌علیه‌های $k$ شکلات می‌دهد. حال از شما می‌خواهیم با دریافت دو عدد $L$ و $R$ میانگین تعداد شکلات‌هایی که امین باید هدیه بدهد را حساب کنید. با توجه به اینکه این عدد یک کسر می‌شود، از شما می‌خواهیم پاسخ را به صورت کسر $P/Q$ به ساده‌ترین شکل ممکن چاپ کنید. # ورودی در سطر اول ورودی، عدد صحیح و مثبت $L$ و در سطر دوم ورودی، عدد صحیح و مثبت $R$ داده می‌شود. $$1 \leq L \leq R \leq 10^{12}$$ # خروجی در تنها سطر خروجی، پاسخ مسئله را چاپ کنید. # مثال‌ها ## ورودی نمونه ۱ ``` 1 4 ```` ## خروجی نمونه ۱ ``` 2/1 ```` ## ورودی نمونه ۲ ``` 11 14 ```` ## خروجی نمونه ۲ ``` 7/2 ````

+ محدودیت زمان: ۲ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- یک دنباله از اعداد صحیح مثل $a_1, a_2, \dots, a_n\,$ داریم. $q$ درخواست داده می‌شود. دو نوع درخواست داریم. در هر درخواست دو عدد صحیح $l$ و $r$ که $1 \leq l \leq r \leq n$ است داده می‌شود از شما می‌خواهیم همه‌ی اعداد $a_l, a_{l+1}, \dots, a_r\,$ را به $f(a_l), f(a_{l+1}), \dots, f(a_r)\,$ تغییر داده و در جایگاه آن بنویسید، و سپس مجموع اعداد همین زیربازه $l$ تا $r$ را بعد از تغییر چاپ کنید. یعنی در هر درخواست یک بازه پشت سر هم از دنباله تغییر می‌کند و هر عدد دنباله تبدیل به $f$ خود می‌شود. مقدار $f(k)$ از رابطه‌ی زیر بدست می‌آید: $$f(k) = \lfloor \sqrt{k} \rfloor . (\lfloor \sqrt{k} \rfloor - 1)$$ # ورودی در سطر اول ورودی، عدد صحیح و مثبت $n$ آمده که تعداد اعضای دنباله‌ی را نشان می‌دهد. $$1 \leq n \leq 100 \, 000$$ در سطر دوم ورودی، $n$ عدد صحیح که با یک فاصله از هم جدا شده‌اند آمده است. عدد $i$ ام ظاهر شده مقدار $a_i$ را نشان می‌دهد. $$1 \leq a_i \leq 1000 \, 000$$ در سطر سوم ورودی، عدد صحیح $q$ آمده که تعداد درخواست‌ها را نشان می‌دهد. $$1 \leq q \leq 1000 \, 000$$ در $q$ سطر بعدی، در هر سطر یک درخواست می‌آید. هر درخواست به صورت دو عدد $l$ و $r$ نشان داده می‌شود که $l$ و $r$ به ترتیب شروع و پایان بازه‌ی درخواست را نشان می‌دهند. $$1 \leq l \leq r \leq n$$ # خروجی به تعداد درخواست‌ها، مقدار مجموع زیربازه را بعد از تغییر گفته شده چاپ کنید. # مثال‌ها ## ورودی نمونه ۱ ``` 5 10 4 11 3 7 3 2 4 1 3 1 5 ```` ## خروجی نمونه ۱ ``` 8 8 4 ````

+ محدودیت زمان: ۱ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- معلم ریاضی خیلی از امین خوشش نمی‌آید و همیشه او را مجبور می‌کند که سخت‌ترین مسائل را پای تخته حل کند. امروز هم او یک دنباله شامل $n$ عدد صحیح غیرمنفی $a_1, a_2, \ldots, a_n$ را روی تخته نوشت و امین را پای تخته صدا زد. در یک حرکت، معلم به امین اجازه می‌دهد که یکی از $n$ عدد روی تخته را پاک کرده و به جای آن عددی به میزان یک واحد بیشتر بنویسد. معلم از امین می‌خواهد که با کمترین تعداد حرکت، به گونه‌ای عمل کند که در این دنباله، عددهای متوالی از 1 تا $h$ در جایی ظاهر شوند. به امین کمک کنید تا بفهمد با کمترین تعداد حرکت می‌تواند به این هدف برسد به طوری که برای حداقل یک $i$ داشته باشیم $a_i=1, a_{i+1}=2, \dots, a_{i+h-1}=h$، یا مشخص کنید که این کار غیرممکن است و معلم دوباره بی‌رحمانه امین را اذیت می‌کند. # ورودی اولین خط فایل ورودی شامل دو عدد طبیعی $n$ و $h$ است. $$1 \le h \le n \le 200\,000$$ دومین خط شامل $n$ عدد $a_i$ است --- مقادیر اولیه عناصر دنباله نوشته شده. $$0 \le a_{i} \le n$$ # خروجی در تنها خط فایل خروجی، کمترین تعداد حرکت‌هایی که امین نیاز دارد تا مسئله را حل کند را بنویسید، یا `-1` اگر این کار غیرممکن است. # مثال ## ورودی نمونه ۱ ``` 4 3 1 1 0 2 ```` ## خروجی نمونه ۱ ``` 3 ```` ## ورودی نمونه ۲ ``` 3 2 1 3 2 ```` ## خروجی نمونه ۲ ``` -1 ````

+ محدودیت زمان: ۱ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- امین می‌خواهد برای یک پروژه‌ی برنامه‌نویسی $n$ ساعت وقت بگذارد. او می‌خواهد این $n$ ساعت را در روزهای خود پخش کند، و بی‌نهایت روز در برنامه‌اش وجود دارد! امین می‌داند اگر یک روز کمتر از $\ell$ ساعت کار کند، احساس بیهودگی می‌کند، همچنین می‌داند اگر بیشتر از $r$ ساعت در یک روز مشغول کد زدن باشد برای سلامتی‌اش ضرر دارد. پس تصمیم دارد عددی صحیح بین $[\ell, r]$ (شامل $\ell$ و $r$ است) ساعت کار کند. او می‌خواهد این پروژه را در صورت امکان، با کمترین تعداد روز ممکن تمام کند. از شما می‌خواهیم برنامه‌ای بنویسید که این کمینه روز را مشخص کند. # ورودی در تنها سطر اول ورودی، عدد صحیح و مثبت $n$ آمده است. $$1 \leq n \leq 10^9$$ در سطر دوم ورودی، دو عدد صحیح و مثبت $\ell$ و $r$ داده می‌شود. $$1 \leq \ell \leq r \leq n$$ # خروجی در تنها سطر خروجی، کمینه تعداد روز لازم برای تمام شدن پروژه را مشخص کنید. اگر انجام این کار شدنی نیست `-1` چاپ کنید. # مثال‌ها ## ورودی نمونه ۱ ``` 10 3 4 ```` ## خروجی نمونه ۱ ``` 3 ```` اگر امین روز اول ۴ و روز دوم و سوم ۳ ساعت کار کند، کل ۴ + ۳ + ۳ = ۱۰ ساعت کار انجام می‌شود. انجام این ۱۰ ساعت در کمتر از ۳ روز با این شرایط ممکن نیست. بنابراین پاسخ مسئله برابر ۱۰ است. ## ورودی نمونه ۲ ``` 4 1 2 ```` ## خروجی نمونه ۲ ``` 2 ```` اگر امین روز اول و دوم ۲ ساعت کار کند، کل ۲ + ۲ = ۴ ساعت کار انجام می‌شود. انجام این ۴ ساعت کار در کمتر از ۲ روز با این شرایط ممکن نیست. بنابراین پاسخ مسئله برابر ۲ است. ## ورودی نمونه ۳ ``` 7 3 3 ```` ## خروجی نمونه ۳ ``` -1 ```` امین هر روز دقیقاً ۳ ساعت کار می‌کند پس او می‌تواند پروژه‌های ۳، ۶، ۹، ... انجام دهد و انجام پروژه‌ی ۷ ساعته ممکن نیست. بنابراین پاسخ مسئله `-1` است.

+ محدودیت زمان: ۱ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- مهدی به مناسبت تولدش یک کیک دریافت کرده است. کیک با دو نوع تزیینات تزئین شده است: گل‌های خامه‌ای و گیلاس‌ها. مهدی می‌خواهد یک تکه از کیک برای خودش ببرد به طوری که حداقل شامل یک گل خامه‌ای باشد اما هیچ گیلاسی در آن نباشد. اگر از بالا به کیک نگاه کنیم، کیک به صورت یک مربع قابل نمایش است. با معرفی یک سیستم مختصات دکارتی با مبدا در مرکز کیک و محورهایی که موازی با اضلاع کیک هستند، مختصات یک گوشه کیک $(-10^6, -10^6)$ و گوشه مخالف آن $(10^6, 10^6)$ خواهد بود. تمام گل‌های خامه‌ای و گیلاس‌ها به طور دقیق در داخل این مربع قرار دارند.  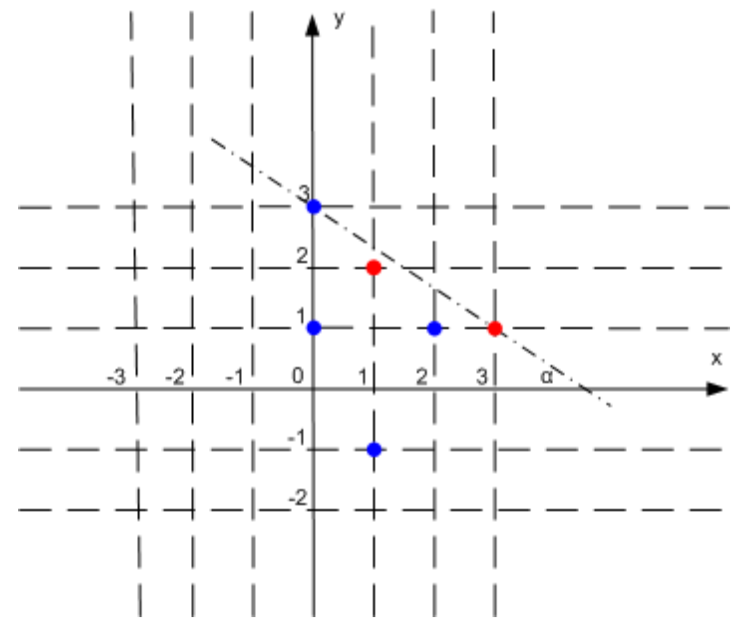برای بریدن یک تکه از کیک، مهدی می‌خواهد یک برش مستقیم انجام دهد. علاوه بر این، برای آسان‌تر کردن برش، او می‌خواهد اندازه زاویه بین خط برش و محور Ox تا حد ممکن کوچک باشد، و اگر یک گیلاس یا گل خانه‌ای دقیقا روی برش بودند، شما بعنوان برش‌دهنده می‌توانید انتخاب کنید که کدام سمت برش بیفتند. وظیفه شما این است که تعیین کنید آیا مهدی می‌تواند کیک را به شکلی که توضیح داده شده برش دهد و کوچکترین زاویه ممکن بین خط برش و محور Ox را پیدا کند. # ورودی خط اول شامل یک عدد صحیح $n$ — تعداد گل‌های خامه‌ای. هر یک از $n$ خط بعدی شامل دو عدد صحیح — مختصات یک گل خامه‌ای. $$1 \leq n \leq 100\,000$$ سپس، یک خط شامل یک عدد صحیح $m$ — تعداد گیلاس‌ها. هر یک از $m$ خط بعدی شامل دو عدد صحیح — مختصات یک گیلاس. $$1 \leq m \leq 100\,000$$ هیچ دو نقطه‌ای که گل‌های خامه‌ای و گیلاس‌ها در آن قرار دارند با هم تداخل ندارند. مختصات گل‌های خامه‌ای و گیلاس‌ها اعدادی صحیح و با قدر مطلق کمتر از $10^6$ هستند. # خروجی اگر برش تکه کیک به روش مشخص شده امکان‌پذیر نباشد، `Impossible` را در فایل خروجی چاپ کنید. در غیر این صورت، کوچکترین زاویه بین خط برش و محور Ox را به صورت رادیان با دقتی نه کمتر از $10^{-4}$ چاپ کنید. # مثال ## ورودی نمونه ۱ ``` 2 1 2 3 1 4 0 1 2 1 0 3 1 -1 ```` ## خروجی نمونه ۱ ``` 0.588002603548 ```` ## ورودی نمونه ۲ ``` 1 1 1 2 0 1 2 1 ```` ## خروجی نمونه ۲ ``` 0 ```` ## ورودی نمونه ۳ ``` 1 10 10 4 10 11 10 9 11 10 9 10 ```` ## خروجی نمونه ۳ ``` Impossible ````

+ محدودیت زمان: ۱ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- می‌خواهیم از بین $n$ نفر از دوستان امین، تعدادی را برای مهمانی تولد دعوت کنیم. امین دوستانش را با اعداد ۱ تا $n$ شماره‌گذاری می‌کند. دوست $i$ام امین به اندازه‌ی $a_i$ با امین صمیمی است. امین می‌خواهد یک زیرمجموعه $k$ عضوی از دوستانش مثل $i_1, i_2, \dots, i_k\,$ را انتخاب کند به طوری که مقدار صمیمت جمع حداکثر شود. صمیمت این جمع که با $s$ نمایش داده می‌شود، از رابطه‌ی زیر بدست می‌آید. $$\frac{1}{s} = \frac{1}{a_{i_1}} + \frac{1}{a_{i_2}} + \dots + \frac{1}{a_{i_k}}$$ به شما میزان صمیمیت امین با دوستانش داده می‌شود. از شما می‌خواهیم برنامه‌ای بنویسید که حداکثر میزان صمیمت ممکن برای مهمانی را محاسبه کند. # ورودی در سطر اول ورودی، عدد صحیح و مثبت $n$ داده می‌شود. $$1 \leq n \leq 200 \, 000$$ در سطر دوم ورودی، $n$ عدد صحیح $a_1, a_2, \dots, a_n\,$ به ترتیب و با فاصله از هم داده می‌شود. $$1 \leq a_i \leq 10^9$$ # خروجی در تنها سطر خروجی، یک عدد اعشاری چاپ کنید که حداکثر میزان صمیمت مهمانی را نشان می‌دهد. پاسخ شما زمانی پذیرفته می‌شود که خطای آن حداکثر $10^{-6}$ باشد. # مثال‌ها ## ورودی نمونه ۱ ``` 5 10 18 12 34 4 ```` ## خروجی نمونه ۱ ``` 34.000000 ```` ## ورودی نمونه ۲ ``` 1 13 ```` ## خروجی نمونه ۲ ``` 13.000000 ````