+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
برای مرحله نهایی کدکاپ ۸، تعدادی بلیت در نظر گرفته شده است؛ تعدادی بلیت استانی به نفر اول هر استان در هر مسابقه تعلق میگیرد و تعدادی بلیت کشوری از مجموع لیگ به ۴۰ نفر برتر تعلق میگیرد. کاپعلی یک دانشجوی منظم است و در همهی ۶ مرحلهی مقدماتی کدکاپ ۸ شرکت کرده و حالا میخواهد بررسی کند آیا به مرحله نهایی راه پیدا میکند یا نه.
بلیت استانی: در هر دور مسابقه، به هر استان یک بلیت تعلق میگیرد به شرط اینکه دستکم **۷ دانشجو** از دانشگاههای استان، در مسابقه کد ارسال کرده باشند و دانشجوی برتر استان (رتبهی اول)، دستکم **۲ سوال** آن مسابقه را حل کرده باشد.
بلیت کشوری: به نفرات برتر جدول کل امتیازات لیگ تعلق میگیرد. حل هر سوال در مسابقات انتخابی، یک امتیاز در جدول لیگ دارد. پس از برگزاری ۶ دور مسابقات انتخابی، **۴۰ نفر برتر** که بیشترین امتیازات را کسب کرده باشند، برنده بلیت کشوری میشوند (در این سوال فرض کنید مهم نیست اگر کسی قبلاً بلیت استانی را دریافت کرده باشد و آن فرد هم در رتبهبندی حساب میشود و لازم نیست افراد بعد از نفر ۴۰ام را چک کنید).
کاپعلی میداند در مسابقهی $k$ام از مراحل انتخابی، $n_k$ دانشجوی هماستان او کد ارسال کرده بودند (شامل خود کاپعلی) و او رتبهی $r_k$ را در استان خود با حل $p_k$ سوال کسب کرده است. همچنین در پایان مراحل انتخابی، رتبهی $R$ را در لیگ کسب کرده است.
حال از شما میخواهیم برای $t$ سناریوی مختلف، بررسی کنید آیا کاپعلی بلیت نهایی کدکاپ را کسب کرده است یا نه.
# ورودی
در سطر اول عدد صحیح $t$ آمده که تعداد سناریوها را نشان میدهد.
$$1 \leq t \leq 10 \, 000$$
اطلاعات هر سناریو در چهار خط آمده است که به شرح زیر است:
در سطر اول هر سناریو، اعداد صحیح $n_1$، $n_2$، $n_3$، $n_4$، $n_5$ و $n_6$ به ترتیب نشاندهنده تعداد شرکتکنندههای استان کاپعلی در مراحل اول تا ششم است. در سطر دوم هر سناریو، اعداد صحیح $r_1$، $r_2$، $r_3$، $r_4$، $r_5$ و $r_6$ به ترتیب نشاندهنده رتبه کسب شده کاپعلی در استان از مرحله اول تا مرحله ششم است.
$$1 \leq r_k \leq n_k \leq 1000$$
در سطر سوم هر سناریو، اعداد صحیح $p_1$، $p_2$، $p_3$، $p_4$، $p_5$ و $p_6$ به ترتیب نشاندهنده تعداد سوالات حل شده توسط کاپعلی در مراحل اول تا ششم است و در سطر چهارم هر سناریو، یک عدد صحیح $R$ داده میشود که رتبه کاپعلی در لیگ است.
$$0 \leq p_k \leq 6, \quad 1 \leq R \leq 1603$$
# خروجی
در تنها خط خروجی، اگر کاپعلی به مرحله فینال راه پیدا کرده `YES` و در غیر این صورت `NO` را خروجی دهید.
# مثالها
## ورودی نمونه ۱
```
4
302 192 138 169 124 138
11 12 27 5 3 9
5 6 4 5 6 4
4
58 54 32 37 50 45
6 9 1 11 8 20
3 3 2 2 2 2
80
1000 1000 1000 1000 1000 1000
1 1 1 1 1 1
6 6 6 6 6 6
1
6 7 7 8 5 9
1 1 2 1 1 2
2 1 2 1 3 3
41
````
## خروجی نمونه ۱
```
YES
YES
YES
NO
````
در ادامه توضیحات بیشتر برای نحوهی بررسی هر سناریو آمده است.
<details class="green">
<summary>
**سناریوی اول:**
</summary>
تعداد شرکتکنندگان در هر ۶ مرحله کافی است (حداقل ۷ نفر). کاپعلی در هر مرحله حداقل ۲ سوال حل کرده، ولی هیچوقت رتبهی اول را کسب نکرده است. بنابراین، بلیت استانی را برنده نشده است. رتبهی کاپعلی در لیگ ۴ است، پس در بین ۴۰ نفر برتر قرار گرفته و بلیت کشوری را کسب میکند. خروجی `YES` است.
</details>
<details class="green">
<summary>
**سناریوی دوم:**
</summary>
تعداد شرکتکنندگان در هر ۶ مرحله کافی است (حداقل ۷ نفر). کاپعلی در هر مرحله حداقل ۲ سوال حل کرده است. او فقط در مرحلهی سوم انتخابی رتبهی اول را کسب کرده و بلیت استانی را بدست آورده است. رتبهی کاپعلی در لیگ ۸۰ است و در بین ۴۰ نفر برتر نیست، اما به دلیل داشتن بلیت استانی، بلیت کشوری را کسب میکند. خروجی `YES` است.
</details>
<details class="green">
<summary>
**سناریوی سوم:**
</summary>
تعداد شرکتکنندگان در هر مرحله کافی است (حداقل ۷ نفر). کاپعلی در هر مرحله رتبه اول را کسب کرده و در هر مرحله حداقل ۲ سوال حل کرده است. بنابراین، شرایط بلیت استانی را در هر ۶ مرحله دارد. همچنین، رتبهی کاپعلی در لیگ ۱ است و در بین ۴۰ نفر برتر قرار دارد، پس شرایط بلیت کشوری را نیز دارد. کاپعلی هر دو بلیت استانی و کشوری را کسب میکند. خروجی `YES` است.
</details>
<details class="green">
<summary>
**سناریوی چهارم:**
</summary>
در مرحلهی اول انتخابی، کاپعلی ۲ سوال حل کرده و رتبهی اول را کسب کرده است، ولی تعداد شرکتکنندگان (۶ نفر) کافی نیست، پس بلیت استانی نمیگیرد.
در مرحلهی دوم انتخابی، تعداد شرکتکنندگان کافی است (۷ نفر) و کاپعلی رتبهی اول را کسب کرده، اما چون کمتر از ۲ سوال حل کرده (۱ سوال)، بلیت استانی نمیگیرد.
در مرحلهی سوم انتخابی، تعداد شرکتکنندگان کافی است (۷ نفر) و کاپعلی حداقل دو سوال را حل کرده، ولی رتبهی اول را کسب نکرده است.
در مرحلهی چهارم انتخابی، تعداد شرکتکنندگان کافی است (۸ نفر) و کاپعلی رتبهی اول را کسب کرده، اما چون کمتر از ۲ سوال حل کرده (۱ سوال)، بلیت استانی نمیگیرد.
در مرحلهی پنجم انتخابی، کاپعلی با حل حداقل دو سوال (۳ سوال) رتبهی اول را کسب کرده، ولی تعداد شرکتکنندگان این مرحله کمتر از ۷ نفر است (۵ نفر)، پس بلیت استانی نمیگیرد.
در مرحلهی ششم انتخابی، تعداد شرکتکنندگان کافی است (۹ نفر) و کاپعلی سه سوال حل کرده، ولی چون رتبهی اول را کسب نکرده، بلیت استانی نمیگیرد.
با توجه به این شرایط، کاپعلی هیچ بلیت استانی دریافت نکرده است و با رتبهی ۴۱ در لیگ، در بین ۴۰ نفر اول قرار ندارد و بلیت کشوری نمیگیرد. خروجی `NO` است.
</details>
بلیت نهایی کدکاپ
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
در کدکاپ سیتی، $n$ خیابان افقی و $m$ خیابان عمودی مانند شکل زیر وجود دارد که هر خیابان افقی و هر خیابان عمودی دقیقاً در یک چهارراه با هم تقاطع دارند. در بالای هر خیابان عمودی یک ماشین به سمت پایین و در پایین آن یک پارکینگ وجود دارد. در سمت راست هر خیابان افقی یک ماشین به سمت چپ و یک پارکینگ در انتهای آن قرار دارد.
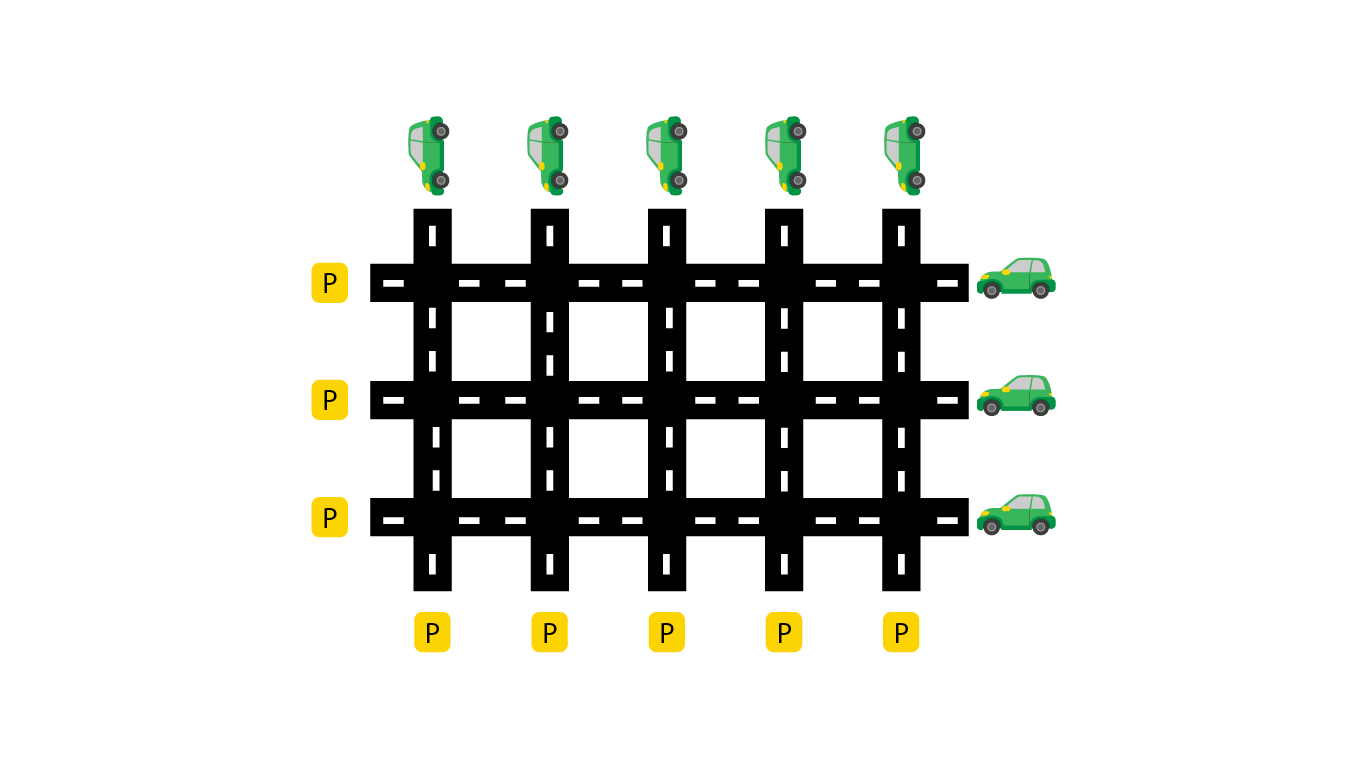
همهی ماشینها در یک لحظه به طور همزمان با سرعت برابر و ثابت شروع به حرکت میکنند. میدانیم عبور از فاصلهی بین دو تقاطع برای یک ماشین، یک دقیقه زمان میبرد. همچنین برای هر ماشین رسیدن به اولین تقاطع نیم دقیقه زمان میبرد و نیم دقیقه زمان میبرد که وارد پارکینگ شود و پارک کند. هرگاه دو ماشین در یک تقاطع به هم برسند یکی از آنها باید یک دقیقه صبر کند تا ماشین دیگر از آن تقاطع عبور کند.
میخواهیم از بین تمام حالتهایی که ممکن است ماشینها در پارکینگ توقف کنند، بررسی کنید کمترین زمانی که لازم است تا همهی ماشینها به پارکینگشان برسند، چقدر است.
# ورودی
در سطر اول ورودی، عدد صحیح $t$ آمده که تعداد سناریوها را نشان میدهد.
$$1 \leq t \leq 10 \, 000$$
در تنها سطر هر سناریو، دو عدد صحیح $n$، $m$ داده میشود که به ترتیب نشاندهنده تعداد خیابانهای افقی و عمودی است.
$$1 \leq n, m \leq 10^9$$
# خروجی
در $t$ سطر، برای هر سناریو به ترتیب حداقل زمان (بر حسب دقیقه) مورد نیاز برای رسیدن تمام ماشینها به پارکینگشان برسند را در خروجی چاپ کنید.
# مثالها
## ورودی نمونه ۱
```
3
4 4
3 5
1 1
````
## خروجی نمونه ۱
```
5
5
2
````
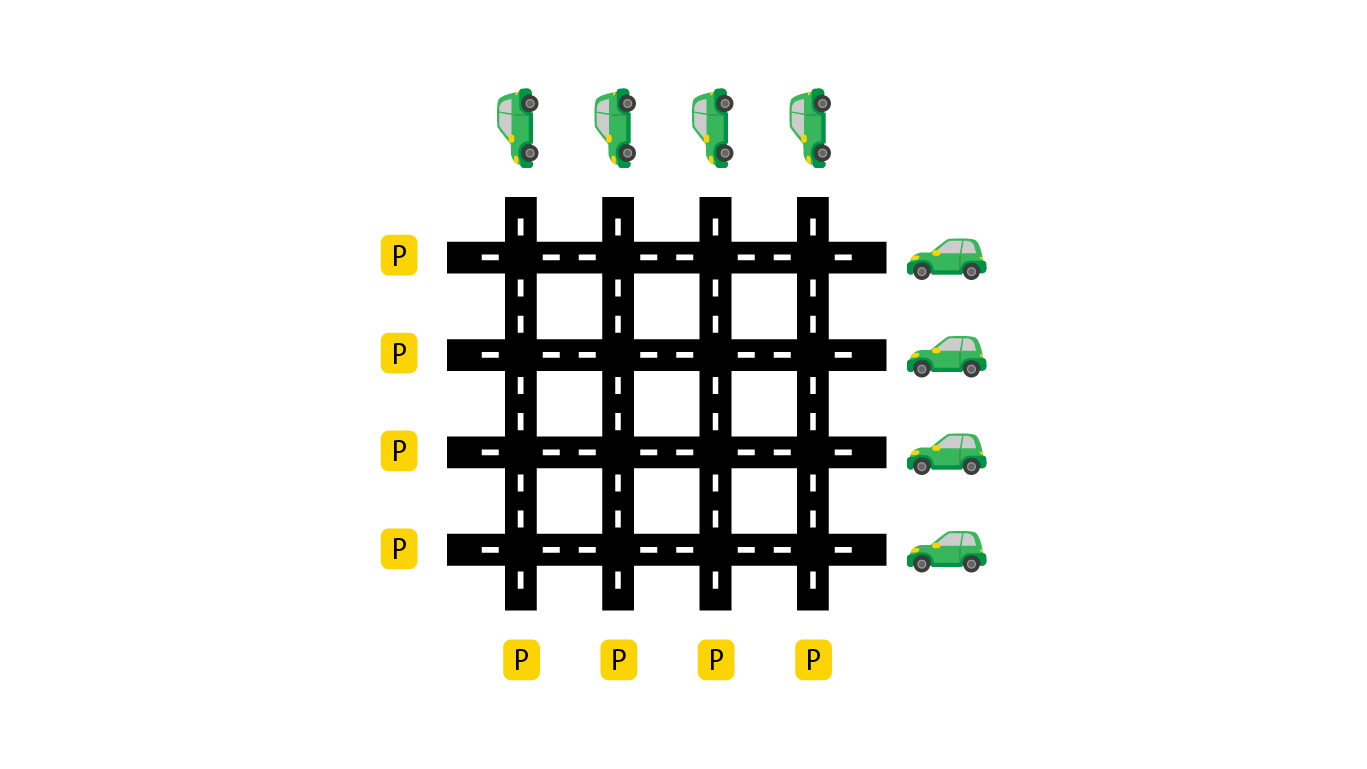
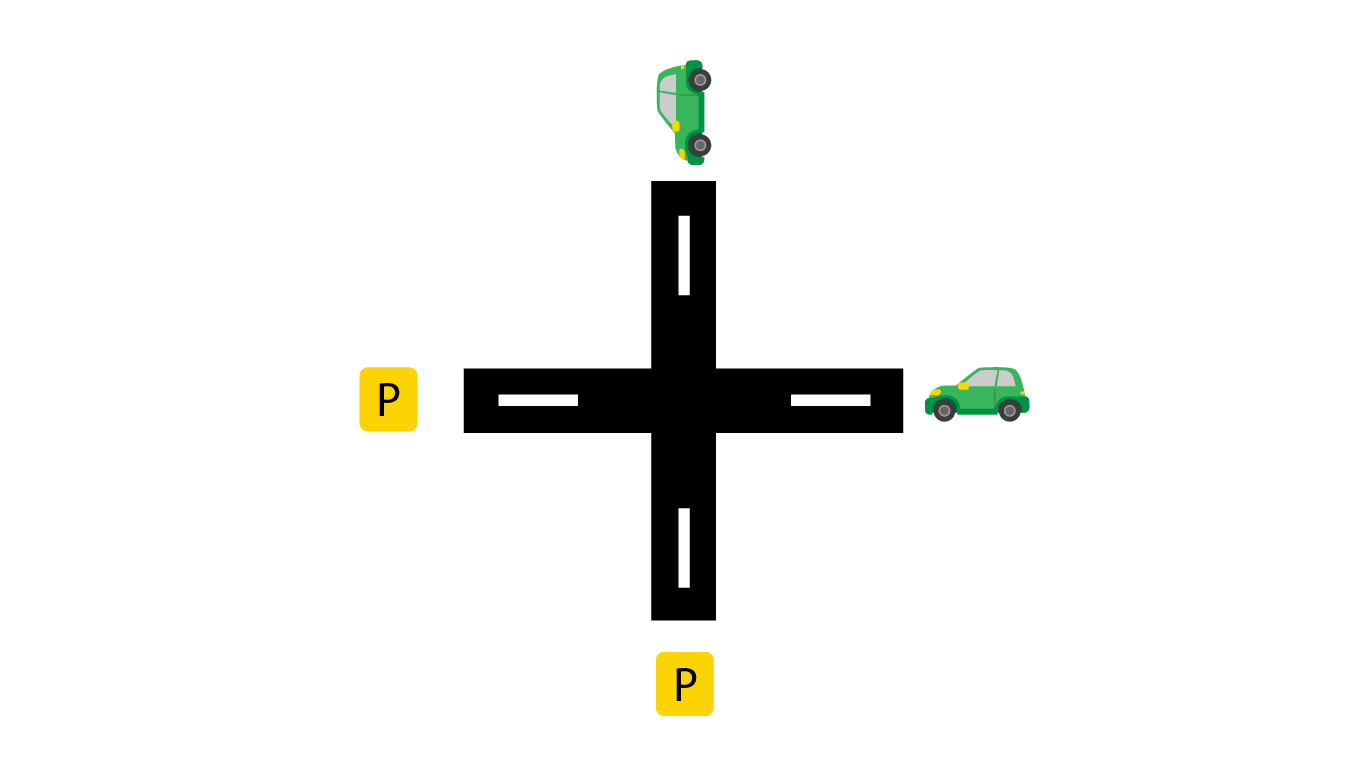
چهارراه کدکاپ
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
در مهمانی شام کدکاپ $n$ دانشجوی علوم کامپیوتر، $m$ دانشجوی مهندسی کامپیوتر و $p$ استاد دانشگاه دعوت شدهاند. در سالن پذیرایی $\frac{n + m + p}{4}$ میز دایرهای ۴ نفره قرار داده شده تا هر مهمان روی یک صندلی بنشیند. میدانیم $n + m + p$ به ۴ بخشپذیر است.

از نظر کوئرا دو نفر که دور یک میز دایرهای **کنار هم** نشستهاند، تشکیل یک زوج خوشحال میدهند، اگر:
+ حداقل یکی از این دو نفر استاد دانشگاه باشد.
+ دو دانشجو با رشتههای مختلف باشند.
حالا میخواهیم مهمانها را طوری روی صندلیهای میز بنشانیم که تعداد زوجهای خوشحال، در مجموع، بیشینه شود. از شما میخواهیم برنامهای بنویسید که این مقدار بیشینه را پیدا کند.
# ورودی
در سطر اول ورودی، عدد صحیح $t$ آمده که تعداد سناریوها را نشان میدهد.
$$1 \leq t \leq 10 \,000$$
در تنها سطر هر سناریو، سه عدد صحیح $n$، $m$ و $p$ که به ترتیب نشاندهنده تعداد دانشجویان علوم کامپیوتر، مهندسی کامپیوتر و اساتید است، داده میشود.
$$0 \leq n, m, p \leq 10^9, \quad n + m + p \geq 4$$
تضمین میشود در هر سناریوها، $n + m + p$ مضرب ۴ باشد.
# خروجی
در $t$ سطر، بیشینهی تعداد زوجهای خوشحال را خروجی دهید.
# مثالها
## ورودی نمونه ۱
```
2
8 2 2
4 0 12
````
## خروجی نمونه ۱
```
8
16
````

در این نمونه، اگر $n = 8$ دانشجوی علوم کامپیوتر روی جایگاه زرد، $m = 2$ دانشجوی مهندسی کامپیوتر روی جایگاه بنفش و $p = 2$ استاد دانشگاه روی جایگاههای سبز بنشینند، ۸ زوج خوشحال که با کمانهای قرمز مشخص شده بهوجود میآید و این، بیشینه تعداد ممکن، در بین تمام حالتها است.
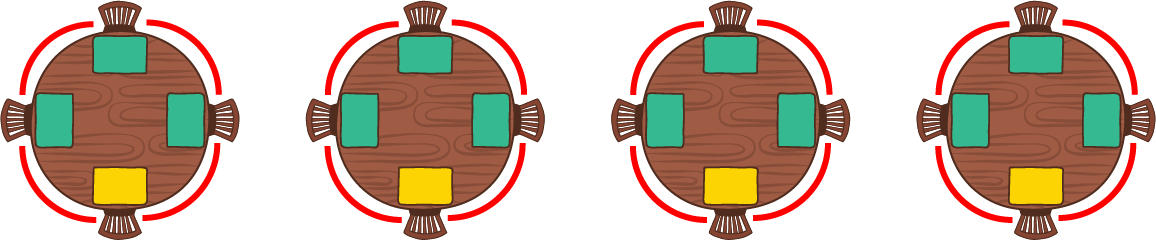
در این نمونه، اگر $n = 4$ دانشجوی علوم کامپیوتر روی جایگاه زرد، و $p = 12$ استاد دانشگاه روی جایگاههای سبز بنشینند، همهی ۱۶ زوج خوشحال میشوند که این، بیشینه تعداد ممکن است.
شام کدکاپ
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
کدکاپ سیتی از $n$ ایستگاه هوایی معلق به نامهای $1, 2, \dots, n$ تشکیل شده است. این ایستگاهها با $n - 1$ پل هوایی به هم متصل هستند و با شروع از هر ایستگاهی میتوانیم به تمام ایستگاهها با استفاده از پلهای هوایی برسیم (ساختار ایستگاهها شبیه به درخت است).
میدانیم کل شهر کدکاپ در هوا معلق است. در این شهر هر ایستگاه برای معلق ماندن باید به حداقل تعدادی از پلهای هوایی متصل باشد. عدد سقوط $f_i$ نشان میدهد ایستگاه $i$ برای معلق ماندن باید به حداقل $f_i$ پل هوایی متصل باشد.
یک تروریست با خود عهد بسته کاری کند که کل شهر کدکاپ سقوط کند. او قرار است در مرکز کنترل تعدادی از ایستگاهها بمب بگذارد. سپس در لحظهای خاص تمام آن ایستگاهها سقوط خواهند کرد و تمام پلهای هواییای که آنها را به ایستگاه های دیگر متصل کرده نیز نابود خواهند شد. سپس تمام ایستگاههایی که با نابودی پلها تعداد پلهای هوایی متصل به آنها از عدد سقوطشان کمتر شده و دیگر نمیتوانند معلق بمانند نیز سقوط میکنند و دوباره تمام پلهای هوایی متصل به این ایستگاهها نیز نابود میشوند. این روند انقدر تکرار میشود تا تمام ایستگاههای باقیمانده حداقل به اندازهی عدد سقوطشان به پلهای هوایی متصل باشند.
با توجه به این که امنیت ایستگاهها متفاوت است. تروریست برای بمبگذاری هر ایستگاه به اندازه عدد امنیتی آن ایستگاه باید تعدادی سکه رشوه دهد. عدد امنیت ایستگاه $i$ام برابر $s_i$ است. کمترین تعداد سکهای که تروریست نیاز دارد تا بعد از بمبگذاری مطمئن باشد تمام ایستگاهها سقوط خواهند کرد چقدر است؟
# ورودی
در سطر اول ورودی عدد طبیعی $t$، تعداد سناریوها داده میشود.
$$1 \leq t \leq 100\, 000$$
در هر سناریو اطلاعات کامل یک کدکاپ سیتی به صورت زیر به شما داده میشود.
در سطر اول هر سناریو عدد طبیعی $n$ که نشانگر تعداد ایستگاهها است به شما داده میشود.
$$1 \leq n \leq 100\, 000$$
سپس در هر کدام از $n - 1$ سطر بعدی اطلاعات پلهای هوایی $i$ام داده میشود. در هر سطر عدد $u_i$ و $v_i$ که نشانگر دو ایستگاهی که توسط پل هوایی $i$ام به هم متصلاند، آمده است.
$$ 1 \leq v_i , u_i \leq n$$
سپس در سطر بعدی $n$ عدد سقوط ایستگاهها به ترتیب داده میشوند.
$$ 0 \leq f_i \leq 100\, 000$$
تضمین میشود در ابتدا کدکاپ سیتی در هوا معلق است پس عدد سقوط هیچ ایستگاه هواییای از تعداد پلهای هوایی متصل به آن بیشتر نیست.
در سطر بعدی به عنوان آخرین سطر ورودی هر سناریو $n$ اعداد $s_i$، نشانگر امنیت ایستگاه $i$ام به ترتیب داده میشوند.
$$ 0 \leq s_i \leq 10^9$$
مجموع $n$ها در تمام سناریوها حداکثر $100 \,000$ است.
$$1 \leq \sum n \leq 100\, 000$$
# خروجی
خروجی شما باید در $t$ خط داده شود. در هر خط کمترین تعداد سکهای که تروریست برای سقوط کل کدکاپ سیتی نیاز دارد را خروجی دهید.
# مثالها
## ورودی نمونه ۱
```
3
3
1 2
2 3
1 1 1
1 1000 2
3
1 2
2 3
1 2 1
1 1000 2
3
1 2
2 3
1 1 1
1 2 3
````
## خروجی نمونه ۱
```
3
1
2
````
سقوط کدکاپ
+ محدودیت زمان: ۱.۵ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
یک دنباله از اعداد طبیعی مثل $a_1, a_2, \dots, a_n\,$ روی یک ردیف نوشته شده است. تخته را به دو دوست به نامهای کدکاپ و دانابینا نشان میدهیم. از آنجایی که آنها دوستان صمیمی هستند، میخواهند راجع به اعداد دنباله با یکدیگر صحبت کنند اما دانابینا نمیتواند اعداد را ببیند. همچنین کدکاپ فقط میتواند به طور غیرمستقیم اعداد دنباله را به او بگوید.
کدکاپ در ابتدا تعداد اعداد دنباله یعنی $n$ را اعلام میکند. سپس از اولین عضو دنباله شروع کرده و به ترتیب برای هر دو عضو متوالی از دنباله، $\text{XOR}$ آنها را محاسبه کرده و اعلام میکند. به عبارت دیگر $n - 1$ عدد $x_1, x_2, \dots, x_{n-1}\,$ که $x_i = a_i \oplus a_{i+1}\,$ است را اعلام میکند.
با اینکه کدکاپ اطلاعات زیادی راجع به اعضای دنباله داده است، برای بهدست آوردن تکتک اعداد دنباله کافی نیست. پس کدکاپ به دانابینا اجازه داده است که دو سوال راجع به دنباله بپرسد.
در هریک از دو سوال دانابینا باید یک مجموعه از اعضای دنباله (نه لزوماً متوالی) را مشخص کند و کدکاپ، $\text{AND}$ آنها را محاسبه کرده و اعلام میکند. سپس دانابینا با توجه به پاسخ کدکاپ، اعداد دنباله را بهدست میآورد. امتیاز نهایی برابر است با تعداد عضو کمتر بین دو مجموعهای که دانابینا در این دو سوال انتخاب کرده است.
بیشترین امتیازی که دانابینا میتواند بگیرد چیست؟ دقت کنید باید $\text{AND}$ اعضای دو مجموعهای که دانابینا از اعضای دنباله انتخاب میکند، اطلاعات کافی برای بهدست آوردن اعداد دنباله را به او بدهد.
# ورودی
در سطر اول ورودی عدد طبیعی $t$، تعداد سناریوها داده میشود.
$$1 \leq t \leq 500$$
هر سناریو در دو سطر به شما ورودی داده میشود. در سطر اول عدد طبیعی $n$ به شما داده میشود.
$$1 \leq n \leq 300\, 000$$
سپس در سطر دوم $n-1$ عدد صحیح $x_1, x_2, \dots, x_{n-1}\,$ به شما داده میشود.
$$ 0 \leq x_i \leq 1000$$
تضمین میشود که $1 \leq \sum n \leq 300\, 000$.
# خروجی
در یک سطر، عدد طبیعی $s$، یعنی بیشترین امتیازی که دانابینا با پرسیدن دو مجموعه و تشخیص دقیق دنباله میتواند بگیرد را خروجی دهید.
# مثالها
## ورودی نمونه ۱
```
3
3
1 3
3
2 3
3
2 1
````
## خروجی نمونه ۱
```
2
2
2
````
نابینای دانا
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
کاپعلی یک جهانگرد است که میخواهد کشور کدکاپ را ببیند. لذت بردن از مسیر برای کاپعلی خیلی مهم است، بنابراین کاپعلی میخواهد تمام جادههایی که میبیند برای او جدید باشند. به زبانی دیگر اگر در مسیرش جادهای باشد که او قبلا از آن عبور کرده باشد، کاپعلی بسیار ناراحت میشود.
کاپعلی میخواهد سه شهر $v$، $u$ و $w$ را انتخاب کند و با شروع از $u$ ابتدا به $v$ برود و سپس از $v$ به $w$ برود و در طول این سفر هیچگاه به دلیل دیدن جادهی تکراری، ناراحت نشود. کاپعلی چند حالت برای انتخاب $v$، $u$ و $w$ دارد؟
# ورودی
در سطر اول ورودی، ابتدا $n$، تعداد شهرهای کدکاپ و سپس $m$، تعداد جادههای کدکاپ آمده است.
$$3 \leq n \leq 100 \, 000$$
$$1 \leq m \leq 200 \, 000$$
در $m$ سطر بعدی، در هر سطر دو عدد $b$ و $a$ آمده که یک جاده را نشان میدهد و مشخص میکند که این جاده شهر $a$ و $b$ را به هم متصل میکند.
$$1 \leq a,b \leq n$$
تضمین میشود هیچ جادهای یک شهر را به خودش متصل نمیکند و بین هر دو شهر حداکثر یک جاده وجود دارد.
توجه کنید که ممکن است از شهری در کدکاپ نتوان به شهری دیگر با استفاده از جادهها رفت.
# خروجی
در تنها سطر خروجی تعداد ($v$، $u$،$w$) هایی را چاپ کنید که کاپعلی میتواند از $u$ به $v$ و سپس به $w$ برود و در این میان هیچ جادهای را بیش از یک بار نبیند.
# مثالها
## ورودی نمونه ۱
```
3 3
1 2
2 3
1 3
````
## خروجی نمونه ۱
```
6
````
## ورودی نمونه ۲
```
7 5
1 2
2 3
3 4
4 5
6 7
````
## خروجی نمونه ۲
```
20
````
## ورودی نمونه ۳
```
7 6
1 2
1 3
2 4
2 5
3 6
3 7
````
## خروجی نمونه ۳
```
54
````
لذت از مسیر
+ محدودیت زمان: ۲ ثانیه
+ محدودیت حافظه: ۵۱۲ مگابایت
----------
روی یک میز، پشت سر هم تعدادی سکه قرار دارد است. این سکهها به ترتیب ارزش $c_1, c_2, \dots, c_n\,$ به این سکهها «کامل» میگوییم هرگاه بتوانیم همهی اعداد ۱ تا $c_1 + \dots + c_n\,$ را با این سکهها پرداخت کنیم.
به شما یک آرایه مثل $c_1, c_2, \dots, c_n\,$ داده میشود و از شما $q$ سوال پرسیده میشود. در هر سوال دو عدد $l$، $r$ داده میشود و از شما میپرسیم آیا آرایهی $c_l, c_{l+1} \dots, c_r\,$ یک مجموعه کامل است یا نه.
# ورودی
در سطر اول ورودی، عدد صحیح و مثبت $n$ داده میشود که تعداد اعداد آرایه را نشان میدهد.
$$1 \leq n \leq 200 \, 000$$
در سطر دوم ورودی، $n$ عدد صحیح $c_1, c_2, \dots, c_n\,$ با فاصله از هم داده میشود.
$$1 \leq c_i \leq 10^9$$
در سطر سوم ورودی، عدد صحیح و مثبت $q$ داده میشود که تعداد سوالات را نشان میدهد.
$$1 \leq q \leq 200 \, 000$$
در $q$ سطر بعدی، در هر سطر دو عدد $l$ و $r$ داده میشود که یک سوال را نشان میدهد.
$$1 \leq l \leq r \leq n$$
# خروجی
در $q$ سطر پاسخ سوالات را به ترتیب چاپ کنید. در صورتی که زیرآرایه پرسیده شده از سکهها کامل است، رشتهی `PERFECT` و در غیر این صورت `NOT PERFECT` را چاپ کنید.
# مثالها
## ورودی نمونه ۱
```
5
1 3 2 8 1
4
1 2
1 3
2 5
1 5
````
## خروجی نمونه ۱
```
NOT PERFECT
PERFECT
NOT PERFECT
PERFECT
````
سکههای کامل
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
برای برگزاری اختتامیه کدکاپ، یک فضای باز در کویری صاف و بیآب و علف در نظر گرفتهایم. از قبل روی زمین $n$ ستون قرار دارد. اگر این محوطه را به صورت صفحهی مختصات دوبعدی در نظر بگیریم. ستونها مانند نقطههایی مثل $(x_1, y_1), (x_2,. y_2), \dots, (x_n, y_n)\,\,\,$ در صفحه هستند.
مدیر مسابقات میخواهد یک طناب دور این ستونها بکشد و محوطه اختتامیه را مشخص کند. او میخواهد طوری این طناب را بکشد، که همهی ستونها داخل محوطه قرار بگیرند و طول طنابی که استفاده میشود، کمینه باشد.
به طرز عجیبی یکی از این $n$ ستون از محوطه حذف شده ولی نمیدانیم کدام ستون است، برای همین برای هر $i = 1, 2, \dots, n\,$ بررسی کنید اگر ستون $(x_i, y_i)$ در زمین نباشد، محیط طنابی که باید بکشیم چقدر است.
همچنین میدانیم هیچ دو ستونی روی هم قرار نگرفته و مساحت ناحیهی مشخص شده برای محوطه، همواره (برای هر ستونی که نباشد)، مثبت بدست میآید.
# ورودی
در سطر اول ورودی، عدد صحیح و مثبت $n$ آمده است.
$$4 \leq n \leq 100 \, 000$$
در $n$ سطر بعدی، در هر سطر دو عدد $x_i$ و $y_i$ آمده که مختصات ستون $i$ام را نشان میدهد.
$$-10^9 \leq x, y \leq 10^9$$
تضمین میشود هیچ دو ستونی روی هم نباشند و مساحت ناحیهی مشخص شده برای محوطه، همواره مثبت بدست میآید.
# خروجی
در $n$ سطر پاسخ مسئلهها را چاپ کنید. در سطر $i$ام حداقل طول طناب مورد نیاز در صورت نبودن ستون $i$ام را چاپ کنید.
پاسخ شما زمانی پذیرفته میشود که اختلاف آن با جواب درست حداکثر $10^{-3}$ باشد.
# مثالها
## ورودی نمونه ۱
```
5
2 0
0 2
0 0
2 1
4 1
````
## خروجی نمونه ۱
```
10.246211251
8.472135955
9.187600728
10.359173603
7.236067977
````
## ورودی نمونه ۲
```
4
-3 0
0 -1
3 0
0 3
````
## خروجی نمونه ۲
```
11.404918347
14.485281374
11.404918347
12.324555320
````