حسن قصد دارد در شبکه مخوف اینترنت یک وبسایت پرآوازه را هک کند پس از تلاش‌های شبانه‌روزی به این نتیجه رسید که رشته‌ای که بین دو طرف رد و بدل می‌شود، رمز با ماکسیمم زیررشته متقارن در آن نسبت بسیار زیادی دارد از آنجا که شما می‌خواهید حسن را در این هک بزرگ کمک کنید این برنامه را برای او بنویسید

ورودی🔗

در تنها خط ورودی رشته‌ای را از ورودی دریافت کنید. طول رشته حداکثر 1000 می‌باشد

خروجی🔗

در تنها خط خروجی بزرگترین زیر رشته متقارن را چاپ کنید. در صورت وجود چند رشته اولین زیر رشته ماکسیمم را چاپ کنید.

مثال:

ورودی نمونه ۱

artrartrt

خروجی نمونه ۱

rtrartr

ورودی نمونه ۲

abacada

خروجی نمونه ۲

aba

لیست راس‌های یک درخت دودویی ( نه لزوما درخت دودویی جستجو ) به صورت پیش‌
ترتیب و میان
‌ترتیب به شما داده می‌شود. شما باید لیست راس
‌های درخت را به صورت پس‌ترتیب چاپ کنید.

توضیح نمایش پیش‌ترتیب، میان‌ترتیب و پس‌ترتیب🔗

توضیح کامل‌تر

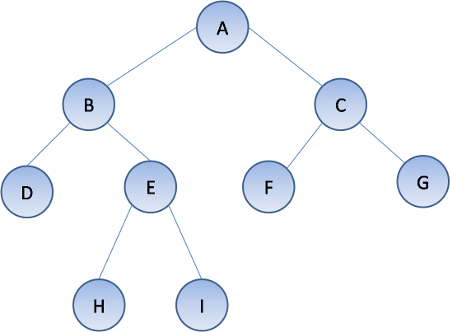
پیمایش پیش‌ترتیب:

1. ریشه را ملاقات کن.
2. زیر درخت چپ را پیمایش کن.
3. زیر درخت راست را پیمایش کن.

• دنباله پیمایش پیش‌ترتیب: A, B, D, E, H, I, C, F, G

پیمایش میان‌ترتیب:

1. زیردرخت چپ را پیمایش کن.
2. ریشه را ملاقات کن.
3. زیردرخت‌ راست را پیمایش کن.

• دنباله پیمایش میان‌ترتیب: D, B, H, E, I, A, F, C, G

پیمایش پس‌ترتیب:

1. زیر درخت چپ را پیمایش کن.
2. زیر درخت راست را پیمایش کن.
3. ریشه را ملاقات کن.

• دنباله پیمایش پس‌ترتیب: D, H, I, E, B, F, G, C, A

ورودی🔗

در خط اول، n تعداد راس‌
های درخت و در خط دوم و سوم، به ترتیب، پیش‌
ترتیب و میان‌
ترتیب درخت دودویی آمده است. برای بیان پیش‌
ترتیب و میان‌
ترتیب در هر خط n عدد که برچسب راس‌های درخت دودویی هستند با فاصله از هم، آمده است. $1 \leq n \leq 10^{4}$

خروجی🔗

در خروجی در یک خط باید n عدد با فاصله از هم جدا شده بنویسید که بیان
گر پس‌ترتیب درخت دودویی باشد.

مثال🔗

ورودی نمونه

8
7 10 4 3 1 2 8 11
4 10 3 1 7 11 8 2

خروجی نمونه

4 1 3 10 11 8 2 7

در آزمایشگاه تحقیقاتی کیهان, موش‌هایی تربیت شده اند که می توانند در کمترین زمان ممکن, به مقصد مورد نظر برسند. آنها می خواهند درستی این قضیه را بررسی کنند. به همین منظور در یک سری محفظه تعدادی موش قرار دادند. (در هر محفظه یک موش)‌ بعضی از محفظه‌ها توسط لوله به هم وصل شده‌اند. (لوله ها به صورت یک طرفه می‌باشند) زمان طی کردن هر لوله برای رسیدن از یک محفظه به محفظه دیگر متفاوت است. اگر یکی از محفظه ها را به دلخواه به عنوان محفظه خروجی بگیریم تا زمان t حداکثر چند موش به محفظه مورد‌نظر می‌رسند.

ورودی🔗

خط اول شامل ۴ عدد صحیح N , M , D , T به ترتیب است. (از چپ به راست) عدد N بیانگر تعداد محفظه هاست. (N<100000) عدد M بیانگر تعداد لوله‌هاست. (M<100000) عدد D بیانگر محفظه مقصد است. ( محفظه ها از 1 تا N شماره گذاری شده اند.) عدد T نیز بیانگر زمان مورد نظر است. (T<10^9) در M خط بعدی اطلاعات لوله‌ها وجود دارد. به این ترتیب که در هر خط سه عدد Src , Dest , Time به ترتیب (از چپ به راست) وجود دارند. این سه عدد بیانگر این است که برای رفتن از محفظه Src به محفظه Dest از طریق این لوله به اندازه Time ثانیه زمان طول می‌کشد. توجه کنید که لوله‌ها یک طرفه می‌باشند.

خروجی🔗

تعداد موش‌هایی که حداکثر تا زمان T به محفظه مورد نظر می‌رسند را چاپ کنید.

نمونه ورودی🔗

4 5 2 50
1 2 50
1 3 20
2 4 10
3 4 11
3 2 10

نمونه خروجی🔗

3

در اقیانوس آرام نواحی ای وجود دارند که به صورت خودمختار اداره می
شوند. این جزایر معمولاً با یک مشکل روب
رو هستند و آن این است که هرکدام از این نواحی از چندین جزیره تشکیل می
شوند که هیچ راه ارتباطی
ای به جز پل های دریایی میان آن
ها وجود ندارد. حال رؤسای ادارات پست این نواحی از شما می خواهند برنامه ای برای آن
ها بنویسید که با گرفتن تعداد همه ی ادارات پست یک ناحیه و سپس دریافت یک ماتریس که شیوه‌
ی ارتباط این ادارات را به هم نشان می
دهد، تعداد دسته‌ی ادارات پستی که با هم ارتباط دارند و با دیگر ادارات پست ارتباط ندارند را معین کند. دقت کنید که در هر کدام از جزیره
‌ها ادارات پست راهی برای رسیدن به هم
دیگر دارند که الزاماً این راه بین دو اداره مستقیم و بدون واسطه نیست. هم
چنین در نظر داشته باشید که بین ادارات پست دو جزیره هیچ ارتباطی وجود ندارد.

ورودی🔗

در ورودی یک عدد$2 \leq n \leq 100$ به عنوان تعداد کل ادارات پست یک ناحیه وارد می
‌شود. سپس درایه
‌های یک ماتریس n*n وارد می
شوند که هر یک از آن
ها ۰ یا ۱ اند. ۰ بودن عضو $v_{ij}$ نشان
‌دهنده‌ی نبود پل بین اداره i-اُم و j-اُم است و ۱ بودن آن نشانه‌
ی وجود پل بین این دو اداره می‌باشد. طبیعتاً ماتریس ورودی متقارن خواهد بود.

خروجی🔗

در خروجی تعداد دسته‌
ی ادارات پستی که با هم ارتباط دارند و با دیگر ادارات پست ارتباط ندارند را چاپ کنید.

نمونه ورودی🔗

4
0 0 1 0
0 0 0 1
1 0 0 0
0 1 0 0 

نمونه خروجی🔗

2

محمد حسین می خواهد یک دنباله‌ی معتبر از پرانتزها را وارد رایانه‌ی جدید خود کند، اما او که به دلیل حساسیت پوستی به هوای آلوده تهران، همواره مجبور است از دستکش استفاده کند، در هنگام استفاده از کیبورد و تایپ کردن این دنباله مشکل دارد و گاهاً پرانتزها را جابه‌جا و یا اشتباه وارد می‌کند. قرار است به او کمک کنید تا حداقل تعداد پرانتزهایی را که باید تغییر کنند تا دنباله دوباره معتبر شود بیابد.

منظور از تغییر یک پرانتز عوض کردن ( با ) یا برعکس است.

دنباله‌ی معتبر به دنباله‌ای گفته می‌شود که تعداد ( ها و )ها در آن برابر باشد. همچنین در هر پیشوند از این دنباله، تعداد )ها حداقل به اندازه‌ی تعداد (ها باشد.

ورودی🔗

یک رشته از پرانتزها به طول زوج، به طوری که طول آن حداکثر $10^5$ کاراکتر است.

خروجی🔗

در تنها سطر از خروجی، حاقل تعداد پرانتزهایی که باید تغییر کنند تا دنباله معتبر شود را چاپ کنید.

مثال🔗

ورودی نمونه ۱

())(

خروجی نمونه ۱

2

ورودی نمونه ۲

))()()((())(()))()()

خروجی نمونه ۲

1

سد $n$ طبقه‌ای دیمونا، بزرگترین سد بنا شده در سرزمین‌های اشغالی است. می‌دانیم در پشت طبقه $i$ام این سد، $W_i$ لیتر آب وجود دارد. هم‌چنین می‌دانیم طیقه $i$ام قادر به تحمل $L_i$ لیتر آب است و اگر میزان آب پشت آن بیشتر از این حد شود، آن طبقه تخریب شده و تمام آب‌های موجود پشت آن به طبقه‌ای که بلافاصله پایین‌تر قرار دارد منتقل می‌شود.

گروه های مبارز فلسطینی قصد دارند پایین‌ترین طبقه این سد (طبقه $n$ام) را تخریب کنند. می‌دانیم تخریب طبقه $i$ام سد با مواد منفجره، $P_i$ واحد هزینه دارد؛ از طرفی دوستان فلسطینی ما با محدودیت بودجه روبه‌رو هستند. شما برای کمک به گروه‌های مبارز فلسطینی به مناطق اشغالی اعزام شده‌اید. الگوریتمی (بهینه) ارائه دهید که حداقل هزینه ممکن برای تخریب پایین‌ترین طبقه سد را بیابد.

ورودی🔗

در خط اول، ورودی شامل $(n)$ تعداد طبقات این سد است.

در ادامه $n$ خط می‌آید که در هر خط ۳ عدد $W_i$ ،$L_i$ ‌و $P_i$ داده خواهد شد.

خروجی🔗

در تنها سطر خروجی، حداقل هزینه برای تخریب پایین‌ترین طبقه این سد را چاپ کنید.

محدودیت‌ها🔗

• $n \leq 1.5 \times 10^4$
• $0 \leq W_i, L_i, P_i \leq 10^6$

مثال🔗

ورودی نمونه

3
1000 1000 1
0 1000 2
2 10 100

خروجی نمونه

3