+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۳۲ مگابایت
----------
There is a promotional offer in a bookstore “Take 3, pay for the 2 more expensive ones”. So, each customer who picks 3 books gets the cheapest one for free. Of course, the customer can take even more books and, depending on the way the books are arranged into groups of three, get the cheapest in each group for free.
For example, let the prices of the books taken by the customer be: [10 3 2 4 6 4 9]. If he arranges them into groups (10, 3, 2), (4, 6, 4) and (9), he will get the books priced 2 from the first group for free and the book priced 4 from the second group. We can see that he won’t get anything for free from the third group because it contains only one book.
The lady working in the bookstore is well-intentioned and she always wants to lower the price for each customer as much as possible. For given book prices, help the lady arrange the books into groups in the best way possible, so that the total price the customer has to pay is minimal.
**Please note:** The lady doesn’t have to arrange the books into groups so that each group contains exactly 3 books, but the number of books in a group needs to be between 1 and 3, inclusively.
# Input
The first line of input contains the integer N, the number of books the customer bought.
The second line contains N integer $C_i$ , the price of each book.
# Output
The first and only line of output must contain the required minimal price.
# Constraints
* $1 \leq N \leq 10^5 $
* $1 \leq C_i \leq 10^5 $
# Sample test data
## input 1
```
4
4 2 3 1
```
## output 1
```
8
```
## input 2
```
6
4 5 4 3 4 2
```
## output 2
```
16
```
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۶۴ مگابایت
----------
You are given a tree of order k with n nodes, in other words, each node can have at most K children. The tree is constructed so it’s of the "lowest energy": the nodes are placed in a new depth of the tree only when all the places (from left to right) in the previous depth have been filled. This is also the order of enumerating the nodes, starting with 1. Image depicts an example of a tree of order 3 with 9 nodes.
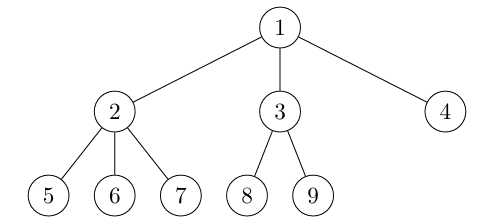
You need to output answers to Q queries in the form of x y, where the answer is the minimal number of steps needed to get from node x to node y.
# Input
The first line of input contains the integers n, k and Q from the task. Each of the following Q lines contains pairs x, y.
# Output
Output Q lines, each line containing the answer to a query from the task.
# Constraint
* $2 \leq n \leq 10^{15} $
* $1 \leq Q \leq 10^5 $
* $1 \leq k \leq 1000 $
# Sample Test Data
## input 1
```
7 2 3
1 4
4 3
5 6
```
## output 1
```
2
3
4
```
+ محدودیت زمان: ۲ ثانیه
+ محدودیت حافظه: ۶۴ مگابایت
----------
A long time ago in the University of Tehran, there were N buildings. There were also $N-1$ pathways that connected all the buildings (directly or indirectly). In other words, the network of buildings and paths formed a tree. Additionally, each path was enumerated with an integer that denoted the curiosity of the path.
A pair of buildings A, B is boring if the following holds:
* A and B are different buildings
* travelling between building A and B is possible using one or more pathways
* binary **XOR** of the curiosity of all the paths in that travel is equal to 0
Unfortunately, times have changed, and an evil dean named Zein is now ruling the department. He decided to use the Force to destroy all the pathways in a **certain order**. Determine the number of boring pairs of buildings before Zein started the destruction and after each destruction.
# Input
The first line of input contains the integer N.
Each of the following $N-1$ line contains three integers $a_i$, $b_i$, $z_i$, that denote that buildings $a_i$ and $b_i$ are directly connected with a path of curiosity $z_i$.
The following line of input contains the permutation of the first $N-1$ integers that denote the order in which Zein is destroying the paths. If the $i^{th}$ element of the permutation is j, then Zein destroyed the path between buildings $a_i$ and $b_i$ in the $i^{th}$ step.
# Output
The output must contain N lines, the $k^{th}$ line containing the number of boring pairs A, B from the task after Zein destroyed exactly $k-1$ paths.
# Constraints
* $1 \leq N \leq 10^5 $
* $1 \leq a_i,b_i \leq N $
* $0 \leq z_i \leq 10^9 $
# Sample Test Data
## input 1
```
3
1 2 5
2 3 5
2 1
```
## output 1
```
1
0
0
```
## input 2
```
4
1 2 0
2 3 0
2 4 0
3 1 2
```
## output 2
```
6
3
1
0
```
+ محدودیت زمان: ۲ ثانیه
+ محدودیت حافظه: ۱۲۸ مگابایت
----------
There are N balloons floating in the air in a large room, lined up from left to right. Young Parva likes to play with arrows and practice her hunting abilities. She shoots an arrow from the left to the right side of the room from an arbitrary height she chooses.
The arrow moves from left to right, at a chosen height $h$ until it finds a balloon. The moment when an arrow touches a balloon, the balloon pops and disappears and the arrow continues its way from left to right at a height decreased by 1. Therefore, if the arrow was moving at height $h$, after popping the balloon it travels on height $h-1$.
Our hero’s goal is to pop all the balloons using as little arrows as possible.
# Input
The first line of input contains the integer N.
The second line of input contains an array of N integers $h_i$
Each integer $h_i$ is the height at which the i-th balloon floats, respectively from left to right.
# Output
The first and only line of output must contain the minimal number of times Parva needs to shoot an arrow so that all balloons are popped.
# Constraints
* $1 \leq N,h_i \leq 10^6 $
# Sample Test Data
## input 1
```
5
2 1 5 4 3
```
## output 1
```
2
```
## input 2
```
5
4 5 2 1 4
```
## output 2
```
3
```
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۶۴ مگابایت
----------
A long, long time ago in a galaxy far, far away a big collision of integers is taking place right now. What happens when two integers collide? During collision, each digit of one number compares itself to the corresponding digit of the other number (the least significant digit with the other’s least significant digit, and so on). The **smaller digit** “falls out” of the number containing it. Additionally, if the digits are the same, **nothing** happens. If a number doesn’t consist of a corresponding digit, then we consider it to be **zero**. After all comparisons of corresponding digits, the leftover digits in the number come closer and create a **new number**. For example:

Write a program that will, for two given integers, determine their values \textbf{after collision}. If it
happens that all the digits of one number fell out, then for that number output the message “Zekiii!”.
# input
e first line of input contains the integer N, one of the integers from the task.
The second line of input contains the integer M, one of the integers from the task.
# Output
The two lines of output must contain the new value of the first and second given integer from the task.
# Constraints
* $1 \leq N,M \leq 10^9 $
# Sample Test Data
## input 1
```
65743
9651
```
## output 1
```
673
95
```
## input 2
```
3412
7586
```
## output 2
```
Zekiii!
7586
```
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۶۴ مگابایت
----------
On the football pitch of the University of Tehran, there is, if we are to believe the Guinness Book of Records, the longest stick in the world. On that stick of $L$ meters in length there are $N$ cheerful chameleons. Each chameleon is moving along the stick with constant speed of 1 m/s in one of two possible directions (left or right) and is colored in one of the possible $K$ colors.
It is known that the chameleons of the University of Tehran worship the ancient ant laws that dictate that the walk along the stick must be continued until the end of the stick is reached (which means getting off it), and when a collision with another chameleon takes place, you must turn 180 degrees and continue the walk in the opposite direction. Additionally, after a chameleon colored in a moving to the left collides with a chameleon colored in b moving to the right, the chameleon moving to the left before the collision takes the color of the chameleon moving to the right before the collision (so, color b), while the chameleon moving to the right before the collision takes a new color $(a + b) \hspace{2pt} mod \hspace{2pt} K$.
If you are given the initial positions, colors and directions of movement of all the chameleons, for each color determine the total trip taken by the chameleons in that color before getting off the stick.
# Input
The first line of input contains the integers $N$, $K$ and $L$ from the task.
he $i^{th}$ of the following $N$ lines contains the integer $d_i$ that denotes the distance between the $i^{th}$ chameleon and the left end of the stick, then the integer $b_i$ that denotes the color of the $i^{th}$ chameleon and the character ‘L’ (Left) or 'R' (Right) that denote the direction of movement of the $i^{th}$ chameleon. All integers $d_i$ will be unique and given in strictly ascending order.
# Output
The output must contain $K$ lines, the $i^{th}$ line containing the total trip taken by the chameleons in color $i$.
# Constraints
* $1 \leq N \leq 10^5 $
* $1 \leq K \leq 40 $
* $1 \leq L \leq 10^6 $
* $0 \leq d_i \leq L $
* $0 \leq b_i \leq K-1 $
## input 1
```
4 3 7
1 0 R
3 0 R
4 1 L
6 2 R
```
## output 1
```
10.0
4.0
1.0
```
## input 2
```
5 4 4
1 1 R
3 3 L
4 2 R
5 0 L
```
## output 2
```
2.5
4.0
2.5
4.0
```
+ محدودیت زمان: ۲ ثانیه
+ محدودیت حافظه: ۶۴ مگابایت
----------
Zeinab is a huge fan of chess and programming, but typical chess soon became boring for her, so she started having fun with rook pieces.
She found a chessboard with $N$ rows and $N$ columns and placed $K$ rooks on it. Zeinab’s game is made of the following rules:
* Each rook’s power is determined by an integer.
* A rook sees all the fields that are in his row or column **except** its own field.
* We say that a field is attacked if the binary **XOR** of all the powers of the rooks that see the field is greater than 0.
Notice that the field a rook is at can be attacked or not.
Initially, Zeinab placed the rooks in a certain layout on the board and will make P moves. After each move, determine how many fields are attacked. Every rook can be moved to any free field on the whole board (not only across column and row).
# Input
The first line of input contains integers N, K and P.
Each of the following K lines contains three integers R, C, X. which denote that initially there is a rook of power X on the field (R, C).
Each of the following P lines contains four integers $r_1$, $c_1$, $r_2$, $c_2$ which denote that the rook has moved from field $(r_1, c_1)$ to field $(r_2, c_2)$.
# Output
The output must consist of P lines, the $k^{th}$ line containing the total number of attacked fields after $k$ moves.
# Constraints
* $1 \leq N \leq 10^9 $
* $1 \leq P,K \leq 10^5 $
* $1 \leq R,C \leq N $
* $0 \leq X \leq 10^9 $
* $0 \leq r_1,c_1,r_2,c_2 \leq N $
# Sample Test Data
## input 1
```
2 2 2
1 1 1
2 2 2
2 2 2 1
1 1 1 2
```
## output 1
```
4
2
```
+ محدودیت زمان: ۵ ثانیه
+ محدودیت حافظه: ۱۲۸ مگابایت
----------
Super Mario, the mad plumber, was hired to construct a water supply network between two locations in a city. The city map can be represented as a R $\times$ S grid. Some cells are not suitable for placing water pipes. Locations Mario needs to connect are placed **directly above** the top left cell of the grid, and **directly below** the bottom right cell.
Each suitable cell Mario can either \textbf{leave empty} or use it for placing one of the following 6 pipe types:

Find the number of ways that pipes can be placed to connect the two locations with a continuous pipe
(water must not be spilled). All placed pipe parts **must be in use**.
Output the solution **modulo 10007**.
# Input
The first line of input contains the integers R and S, the number of rows and columns of the city grid, respectively. Each of the next R lines contains exactly S characters: ‘$\cdot$’ if the cell is suitable for placing pipes, and ‘$\#$’ if not.
# Output
The first and only line of output must contain the required number of ways modulo 10007.
# Constraints
* $2 \leq R,S \leq 10 $
# Sample Test Data
## input 1
```
3 3
...
...
...
```
## output 1
```
12
```
## input 2
```
3 2
...
.#.
```
## output 2
```
1
```
# Sample description
In the second sample, this is the only possible solution:
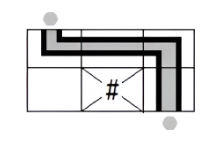
+ محدودیت زمان: ۲ ثانیه
+ محدودیت حافظه: ۶۴ مگابایت
----------
Saeed didn’t want to study solo so he invited his friend Pouya to come over. After an eventful evening that will be remembered for a record number of solved tasks from the field of electronics, Pouya went home. To his surprise, the police stopped him thinking he was drunk! It is known that in these
situations sobriety is proven by solving a series of carefully crafted tasks that test a man’s cognitive abilities. If we can trust Pouya, the conversation went something like this:
**Policeman:** Say the English alphabet in reverse.
**Pouya:** Trivial, zyxwvutsrqponmlkjihgfedcba
**Policeman:** You learned that by heart. Now imagine that all the letters of the English alphabet from 'a’ to ‘z’ are respectively written clockwise in a circle. Begin with the letter ‘a’ and say the letters clockwise. After each spoken letter, I can tell you to continue saying the alphabet in reverse order or
I can ask you how many times so far you’ve said a certain letter. Are you ready? 3, 2, 1, Go!
**Pouya:** Um... a, b, c ...
Write a program that solves Pouya’s problem.
# Input
The first line of input contains the integer Q, the number of policeman’s orders.
Each of the following Q lines contains one of the policeman’s order in the form of **“Change n”** or **“Query n x”**. The order in the form **“Change n”** means
that, after the n-th spoken letter, Pouya must start saying the alphabet in reverse, whereas the order in the form **“Query n x”** means that Pouya must say how many times so far he’s said the letter x in the first n spoken letters.
The policeman’s order will be given chronologically in the input, or, the numbers n from the orders will be strictly ascending. The character x from the order in the form of **“Query n x”** is a lowercase letter of the English alphabet.
# Output
For each order in the form of **“Query n x”**, output how many times Pouya has said the letter x in the first n spoken letters. The answer to each query needs to be written in a separate line, and the queries need to be answered in the order given in the input.
# Constraints
* $1 \leq Q \leq 10^5 $
* $1 \leq n \leq 10^9 $
# Sample Test Data
## input 1
```
5
Change 1
Change 2
Change 3
Query 5 a
Query 7 w
```
## output 1
```
1
```
## input 2
```
5
Query 100 a
Query 200 c
Query 300 a
Query 400 b
```
## output 2
```
4
8
12
16
```
+ محدودیت زمان: ۴ ثانیه
+ محدودیت حافظه: ۳۲ مگابایت
----------
In a two-dimensional coordinate plane, there are N distinct points given as input, specified by their coordinates $(x_i, y_i)$ for $i = 1, 2, ..., N$. Your task is to develop a program that computes the number of unique Orthogonal (right) triangles that can be formed by selecting any three of the provided points.
An Orthogonal triangle is a triangle in which one of the angles measures exactly 90 degrees.
# Input
The first line of input contains an integer N, the number of points.
Each of the following N lines contains the coordinates of one point, two integers $(x_i, y_i)$ separated by a space. No two points will be located at the same coordinates.
# Output
Output the number of Orthogonal triangles.
# Constrints
* $3 \leq N \leq 1500 $
* $-10^9 \leq x_i,y_i \leq 10^9 $
# Sample Test Data
## input 1
```
5
1 1
1 0
0 0
-1 0
-1 1
```
## input 2
```
7
```
+ محدودیت زمان: ۵ ثانیه
+ محدودیت حافظه: ۱۲۸ مگابایت
----------
Hadi is an art dealer. He has **N** clients and sells artistic paintings to each client. Each client can purchase either colored paintings or black and white paintings, but not both. The client denoted with **i** wants to purchase at most $a_i$ colored paintings and at most $b_i$ black and white paintings.
The client will always purchase \textbf{at least one} paintings. Hadi has an almost unlimited amount of paintings, so the number of paintings required from the clients is never a problem. Hadi doesn’t like selling black and white paintings and knows that if less than \textbf{C} people get colored paintings, it will make him feel sad.
His clients constantly keep changing their requests or, in other words, the number of paintings they want to purchase. Because of this, Hadi is often troubled by the question: “How many different purchases are there, so that at least **C** clients get at least one colored painting?” Help Hadi and save him from his worries.
# Input
The first line of input contains two integers N, C.
The second line of input contains N integers $a_i$.
The third line of input contains N integers $b_i$.
The fourth line of input contains the number of requirement changes Q.
Each of the following Q lines contains three integers, the label of the person changing the requirements P, the maximal number of colored paintings they want to purchase $a_p$ and the maximal number of black and white paintings they want to purchase $b_p$.
# Output
The output must consist of Q lines where each line contains the number of different purchases **modulo 10007**.
# Constraints
* $1 \leq N,Q \leq 10^5 $
* $1 \leq a_i,b_i,a_p,b_p \leq 10^9 $
* $1 \leq C \leq 20 $
# Sample Test Data
## input 1
```
2 2
1 2
2 3
2
1 2 2
2 2 2
```
## output 1
```
4
4
```
## input 2
```
4 2
1 2 3 4
1 2 3 4
1
4 1 1
```
## output 2
```
66
```