+ محدودیت زمان: ۲ ثانیه
+ محدودیت حافظه: ۵۱۲ مگابایت
*****

چند روز پیش و مصادف با روز بعد از اعلام نتایج امتحان هندسهی
میانترم، کاراکتر کمکی ۱ در
انباری خانهشان یک صفحه بازی پیدا کرده که متعلق به پدربزرگ مرحومش (خدا رفتگان
شما را هم بیامرزد) است. کاراکتر کمکی ۱ با پیداکردن این صفحهی بازی بسیار خوشحال میشود و تصمیم میگیرد با دوستش کاراکتر کمکی ۲ برای این صفحهی بازی، بازیای ابداع کنند که با انجام آن اندکی از ناراحتی و غم جانسوز اعلام نتایج امتحان هندسه فاصله بگیرند.
از آنجایی که قبل از اینکه قرار باشد بازی ابداع شود آنها حتما باید نسبت به صفحهی بازی شناخت پیدا کنند. پس به همین منظور راهنمای صفحهی بازی را مطالعه میکنند که اطلاعات مندرج در آن به شرح زیر است:
+ صفحهی بازی شامل $n$ دایره و $n - 1$ پاره خط است که هر سر هر پارهخط به یکی از دایرهها متصل است.
+ دایرههای صفحه با اعداد متمایز ۱ تا $n$ شمارهگذاری شدهاند.
+ دو دایره را در صفحهی بازی همسایه مینامیم اگر و فقط اگر یکی از پارهخطهای صفحه باشد که یک سر آن به یکی از این دو دایره و سر دیگرش به دایرهی دیگر متصل باشد.
+ منظور از **حرکت مهره** در این صفحهی بازی، حرکت دادن مهره از دایرهای که روی آن قرار دارد به یکی از همسایههای خالی از مهرهی آن است.
+ اگر فقط یک مهره بر روی یکی از دایرههای صفحه داشته باشیم (برخلاف شرایط بازی) تضمین میشود میتوان با چندبار حرکت دادن مهره، آن را به هر یک از دایرههای دیگر صفحه رساند.
بعد از مطالعهی کامل جزئیات دفترچهی راهنما که در بالا آمده بود، کاراکتر کمکی ۱ و کاراکتر کمکی ۲ توانستند یک بازی بسیار مهیج برای این صفحهی بازی ابداع کنند که مشخصات آن به شرح زیر است:
+ بازی دو نفره است.
+ هر بازیکن یک مهرهی مخصوص به خود دارد. (بازیکنها در حین بازی میتوانند وضعیت مهرهی حریف را ببینند)
+ هر یک از دو مهره در ابتدا و حین بازی روی یکی از دایرههای صفحه قرار میگیرند.
+ هیچگاه دو مهره در یک دایره قرار نمیگیرند.
+ با شروع از کاراکتر اصلی ۱، به نوبت هر بازیکن یکبار مهرهی خود را حرکت میدهد.
+ بازندهی بازی کسی است که نتواند حرکتی انجام بدهد. یعنی دایرهی همسایهی خالیای برای او وجود نداشته باشد که بتواند مهرهاش را به آن حرکت دهد.
دارندهی استراتژی برد، کسی است که با هر نوع بازی طرف مقابل، بتواند طوری بازی کند که در انتها، بازی حتما به نفع خودش تمام شود.
برنامهای بنویسید که دارندهی استراتژی برد در بازی را مشخص کند.
# ورودی
در خط اول ورودی عدد طبیعی $n$ داده میشود که نشان دهنده تعداد دایرههای صفحهی بازی است.
در $n -1 $ خط بعدی در هر خط شمارهی دو دایره آمدهاند که نشاندهندهی وصلبودن این دو دایره توسط یکی از پارهخطهای صفحه است.
در خط آخر دو عدد طبیعی $x$ و $y$ داده میشود که به ترتیب نشاندهندهی شماره دایرهی محل ابتدایی مهرهی کاراکتر کمکی ۱ و کاراکتر کمکی ۲ است.
$$2 \leq n \leq 100 \ 000$$
# خروجی
در تنها خط خروجی اگر کاراکتر کمکی ۱ دارندهی استراتژی برد است، `karakter e komaki_1` را چاپ کنید و اگر کاراکتر کمکی ۲ دارندهی استراتژی برد است، `karakter e komaki_2` را چاپ کنید.
# مثال
## ورودی نمونه ۱
```
3
1 2
1 3
1 2
```
## خروجی نمونه ۱
```
karakter e komaki_2
```
## ورودی نمونه ۲
```
4
1 2
1 3
1 4
3 1
```
## خروجی نمونه ۲
```
karakter e komaki_2
```
## ورودی نمونه ۳
```
7
1 2
1 6
2 3
2 4
2 5
6 7
3 7
```
## خروجی نمونه ۳
```
karakter e komaki_1
```
# توضیح
در مثال اول مهرههای کاراکتر کمکی ۱ و کاراکتر کمکی ۲ به ترتیب در دایرههای ۱ و ۲ قرار دارند. در حرکت اول کاراکتر کمکی ۱ تنها میتواند به دایرهی ۳ برود. در حرکت بعدی کاراکتر کمکی ۲ نیز تنها یک حرکت دارد و میتواند به دایرهی شمارهی ۱ برود. حرکت بعدی نوبت کاراکتر کمکی ۱ است که هیچ دایرهی همسایهی خالی ندارد، پس برندهی بازی کاراکتر کمکی ۲ است.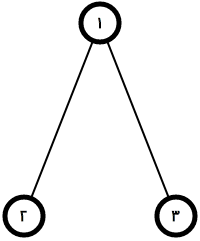
در مثال دوم مهرههای کاراکتر کمکی ۱ و کاراکتر کمکی ۲ به ترتیب در دایرههای ۳ و ۱ قرار دارند. در حرکت اول کاراکتر کمکی ۱ هیچ حرکتی نمیتواند انجام بدهد و در همین حرکت اول و بدون هیچ حرکت مهرهای کاراکتر کمکی ۲ برندهی بازی است.

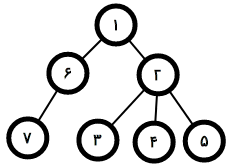
در مثال سوم مهرههای کاراکتر کمکی ۱ و کاراکتر کمکی ۲ به ترتیب در دایرههای ۳ و ۷ قرار دارند. در حرکت اول کاراکتر کمکی ۱ مجبور است مهرهاش را به دایرهی ۲ ببرد. در حرکت بعدی کاراکتر کمکی ۲ هم مجبور است مهرهاش را به دایرهی ۶ ببرد. از اینجا به بعد که برای هر یک از دو بازیکن چند حرکت ممکن وجود دارد، برای کاراکتر کمکی ۱ روش برد ارائه میدهیم. کاراکتر کمکی ۱ میتواند مهرهاش را به دایرهی ۱ ببرد تا کاراکتر کمکی ۲ را مجبور کند در مرحلهی بعد مهرهاش را به دایرهی ۷ ببرد و در حرکت آخر کاراکتر کمکی ۱ مهرهاش را به دایرهی ۶ میبرد تا کاراکتر کمکی ۲ حرکت ممکنی در نوبتش نداشته باشد و برندهی بازی کاراکتر کمکی ۱ شود.
میانترم هندسه
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
*****

پس از امتحان میانترم هندسه، اینبار کاراکتر اصلی که به تازگی خوی مبارزه با دانشآموز
گرفته است سعی دارد از طریق امتحان پایانترم هندسه دانشآموزان بیگناهش (که آنها را با نام کاراکترهای کمکی میشناسیم) را مورد آزار
قرار دهد.
کاراکتر کمکی ۱ و کاراکتر کمکی
۲ که هر دو به شدت امتحانشان را خراب کردند به فکر راهی برای انتقام افتادند.
انتقام از معلم هندسهی
نابکارشان ناشدنی بهنظر میرسد پس به این نتیجه رسیدند که لااقل از برگههای
امتحانی انتقام بگیرند تا گوشهای از عقدهی گوشهی دلشان باز شود. همانطور که میدانید
آنها تنها نیستند و با $n - 2$ دانشآموز فلک زدهی دیگر دست به یکی کردند تا
در روزی مشخص پس از مدرسه جمع شوند و $n$
برگهی امتحانیشان را در یک جمع دانشآموزی مورد محاکمه قرار بدهند. آنها در
دادگاه دانشآموزی بین خودشان حکمی برای این برگهها صادر کردند که کاراکتر کمکی ۱
و کاراکتر کمکی ۲ مامور اجرای این حکم هستند. برای هیجان انگیزتر شدن اجرای حکم
قضایی، کاراکتر کمکی ۱ و کاراکتر کمکی ۲ تصمیم گرفتند حکم را به یک بازی بین
خودشان تبدیل کنند.
هدف بازی مجازات همهی $n$ برگهی امتحانی است و قرار است به ترتیبی این مجازات توسط دو بازیکن بازی یعنی کاراکتر کمکی ۱ و کاراکتر کمکی ۲ انجام شود. قوانین انجام بازی به شرح زیر است:
+ در ابتدا $n$ برگهی
امتحانی باید در یک ردیف قرار بگیرند.
+ هر برگهی امتحانی با توجه به
مقدار سختگیری کاراکتر اصلی در تصحیح آن باید مجازات شود، مجازات به این ترتیب است
که یک نفر از بین کاراکتر کمکی ۱ و کاراکتر کمکی ۲ به سمت برگهی $i$ام با **_میزان نفرت_** $a_i$ شلیک میکند.
(دقت کنید ممکن است میزان نفرت مجازات منفی باشد)
+ بازی نوبتی است و چون کاراکتر کمکی ۱ از لحاظ سنی (و نه از لحاظ عقلی)
بزرگتر است، بازی را شروع میکند.
+ در هر مرحله بازیکنی که نوبتش
است مختار است یکی از برگهها
را به دلخواه به عنوان هدف انجام مجازات انتخاب کند، وقتی برگهای انتخاب شود تمام
برگههای با شمارهی کمتر از آن برگه خود بخود با دیدن مجازات برگهی مجازات شده،
مجازات میشوند، به عبارت دیگر اگر $i$امین برگه
برای مجازات انتخاب شود تمام برگههای مجازاتنشدهی با شمارهی کمتر از $i$ هم مجازات میشوند.
(هیچ برگهای دوبار مجازات نمیشود)
+ مجموع میزان نفرتهای **مفید** شلیکهای انجام
شده توسط هر فرد امتیاز فرد در بازی را مشخص میکند. مجموع میزان نفرتهای **مفید** شلیکها یعنی مجموع میزان نفرت لازم برای مجازات تمام برگههای انتخابشده توسط هر فرد __و نه تمام برگههای مجازات شده توسط فرد__.
همانطور که قبلا هم اشاره شد
در هوش کاراکتر کمکی ۱ و کاراکتر کمکی ۲ شکی نیست، پس یقین داریم بهترین انتخابها
را برای کسب بیشترین مجموع مجازات انجام خواهند داد.
در خروجی دو چیز از شما میخواهیم:
+ مشخص کنید چه کسی میبرد. (کسی که امتیاز بیشتری کسب کند برندهی بازی است)
+ اگر مطلوب علاوه بر بردن بازی،
با بیشینه اختلاف بردن باشد، شخصی که میبرد (در صورتی که بازی به مساوی کشیده نشود) حداکثر با چه اختلاف تضمینشدهای برندهی بازی میشود؟
# ورودی
در خط اول ورودی عدد طبیعی $n$ داده میشود.
در خط بعدی ورودی $n$ عدد طبیعی داده میشود که $i$امین عدد نشاندهنده میزان نفرت لازم برای مجازات برگهی $i$ام است.
$$1 \leq n \leq 1 \ 000 \ 000$$
$$|a_i| \leq 1 \ 000 \ 000 \ 000$$
# خروجی
در صورتی که بازی با بازی هوشمندانهی دوطرف به مساوی ختم شود، `mosavi` را چاپ کنید،
در صورتی که کاراکتر کمکی ۱ بازی را ببرد، `< اختلاف > :karakter e komaki_1` را در خروجی چاپ کنید و در صورتی که کاراکتر کمکی ۲ بازی را ببرد، `< اختلاف > :karakter e komaki_2` را در خروجی چاپ کنید.
# مثال
## ورودی نمونه ۱
```
6
1 2 100 4 5 99
```
## خروجی نمونه ۱
```
karakter e komaki_1: 99
```
## ورودی نمونه ۲
```
2
-10 -10
```
## خروجی نمونه ۲
```
mosavi
```
## ورودی نمونه ۳
```
1
-1
```
## خروجی نمونه ۳
```
karakter e komaki_2: 1
```
# توضیح
در مثال اول همان اولین مجازات برای کاراکتر کمکی ۱ کافی است تا بازی را با بیشترین اختلاف ببرد و با انتخاب برگهی ۶ام بازی را با ۹۹ امتیاز اختلاف، به نفع خودش پایان دهد.
در مثال دوم اگر در مجازات اول کاراکتر اصلی ۱ برگهی شمارهی ۲ را انتخاب کند بازی را با ۱۰ امتیاز اختلاف میبازد، پس برگهی شمارهی ۱ را انتخاب میکند و بازی مساوی میشود.
در مثال سوم تنها انتخاب کاراکتر کمکی ۱ برای انتخاب کردن برگهی شمارهی ۱ است، پس آن را انتخاب میکند و بازی به نفع کاراکتر کمکی ۲ با ۱ امتیاز اختلاف تمام میشود.
پایانترم هندسه
+ محدودیت زمان: ۲ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
*****

کاراکترهای کمکی در روز رسمی اعتراض به نمرات امتحان هندسهی پایانترم، هیئتی برای مذاکره با کاراکتر اصلی ۱ میفرستند. خوشبختانه کاراکتر اصلی ۱ اهل معامله است و حاضر است دو نوع معامله با هیئت مذاکرهکننده انجام دهند:
1. نمرهی هندسهی $k$ نفر از کاراکترهای کمکی را (به انتخاب هیئت مذاکرهکننده) از کارنامهشان حذف کند و در ازای اینکار $x \times k$ تومان پول دریافت کند، که $x$ یک عدد طبیعی مشخص و $k$ یک عدد طبیعی دلخواه هستند.
2. نمرهی هندسهی $k$ نفر از کاراکترهای کمکی را (به انتخاب هیئت مذاکرهکننده) یک نمره افزایش دهد و در ازای اینکار $y \times k$ تومان پول دریافت کند، که $y$ یک عدد طبیعی مشخص و $k$ یک عدد طبیعی دلخواه هستند.
توجه کنید هیئت مذاکرهکننده میتواند تنها یک بار از هر نوع معامله استفاده کند.
هدف هیئت مذاکرهکننده فقط یک چیز است و آن هم این است که لیست نمرات هندسهی کاراکترهای کمکی **شرمآور** نباشد.
لیست نمرات هندسهی کاراکترهای کمکی را **شرمآور** میدانیم در صورتی که تهی نباشد (یعنی حداقل نمرهی هندسهی یکی از کاراکترهای کمکی در کارنامهاش آمده باشد) و ب.م.م (بزرگترین مقسومعلیه مشترک) نمرات ۱ باشد.
در خروجی برنامهی خود چاپ کنید، حداقل میزان پولی که باید کاراکترهای کمکی پرداخت کنند تا لیست نمرات هندسه از **شرمآور**بودن خارج شود، چند تومان است.
# ورودی
در خط اول ورودی سه عدد طبیعی $n$، $x$ و $y$ به ترتیب نشاندهندهی تعداد نمرات لیست اولیهی نمرات هندسه، ضریب قیمت معاملهی اول و ضریب قیمت معاملهی دوم داده شدهاند.
در خط دوم و آخر ورودی، $n$ عدد طبیعی که نشاندهندهی لیست اولیهی نمرات هندسهی کاراکترهای کمکی هستند داده شدهاند. (بیشینه نمرهی قابل کسب در امتحان هندسه برای هر نفر $1 \ 000 \ 000 $ است.)
$$1 \leq n \leq 100 \ 000$$
$$1 \leq x,y \leq 1 \ 000\ 000 \ 000$$
# خروجی
در تنها خط خروجی کمترین هزینهی ممکن هیئت مذاکره کننده برای رسیدن به هدف را چاپ کنید.
# مثال
## نمونه ورودی ۱
```
1 5 1
1
```
## نمونه خروجی ۱
```
1
```
## نمونه ورودی ۲
```
1 4 3
8
```
## نمونه خروجی ۲
```
0
```
## نمونه ورودی ۳
```
5 7 12
1 2 4 8 16
```
## نمونه خروجی ۳
```
7
```
# توضیح
در مثال اول ب.م.م (۱) = ۱ در نتیجه یا باید یکی به ۱ اضافه کنیم یا آن را از لیست نمرات حذف کنیم که افزایش نمره در اینجا ارزانتر است.
در مثال دوم لیست اولیهی نمرات هندسه مطلوب است و هیئتمذاکرهکننده بدون پرداخت هزینهای هدف موردنظر را دارد و نیازی به معامله ندارد.
در مثال سوم هرکاری روی هر یک از اعداد لیست نمرات بکنیم ولی روی ۱ تغییری ایجاد نکنیم همچنان ب.م.م اعداد ۱ خواهد بود. پس با افزایش یا حذف روی ۱ در یک معامله میتوانیم ب.م.م نمرات را به ۲ تغییر بدهیم که در اینجا حذف ارزانتر است از افزایش.
نمرات شرمآور
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
*****

آخرین فرصت برای درس خواندن
کاراکترهای کمکی شهریورماه است. ماهی که کاراکتر اصلی ۱ به مدیر مدرسه قول داده درپایان
آن شمار دانش آموزان را به کمتر از نصف کاهش دهد. متاسفانه هندسهی کاراکترهای
کمکی بسیار ضعیف است درعوض سیستمهای اطلاعاتی بسیار قدرتمندی دارند که از طریق آنها به
تصمیمات شوم کاراکتر اصلی ۱ پی بردهاند. از اینرو برنامهریزی برای پایهریزی
انقلاب دانشآموزی در مدرسه را آغاز کردهاند.
با زحمات شبانهروزی تمام
کاراکترهای کمکی، سرانجام کاراکترهای کمکی موفق به ترسیم نقشهای از مدرسه شدند، کاراکتر کمکی ۱ با اولین نگاه به آن بدرستی متوجه شد که نقشهی مدرسهشان یک
درخت است که هر قسمت مدرسه در آن بصورت یک راس شمارهدار نشان داده شده است و شمارهی هر راس متفاوت از بقیه و عددی طبیعی از ۱ تا $n$ است (شامل خود ۱ و $n$). کاراکتر کمکی ۲ با توجه به حدس کاراکتر کمکی ۱ فکری کرد که به نظر
میتواند آنها را در رسیدن به هدفشان و اینبار، گرفتن انتقام از خود کاراکتر اصلی
۱ یاری کند. ایدهی او این بود که تعدادی از
کاراکترهای کمکی در تعدادی از
برگهای نقشه قرار گیرند (ممکن است تعدادی از برگها باشند که هیچیک از کاراکترهای کمکی در آن نباشند)
سپس یکی از کاراکترهای کمکی با گفتن رمز "هندسه خر عست" عملیات قطعی برق
را آغاز کند. پس از قطعی برق زمان فرار کاراکتر اصلی ۱ از مدرسه فرا میرسد. او که
در مدرسه تنها و بدون کمک هیچ کاراکتر اصلی دیگری گیر افتاده است در ابتدا در راس
۱ نقشهی مدرسه است و بدلیل قطعی برق حتی نمیداند که در حین فرار در هر مرحله به
کجا میرود.
کاراکتر اصلی ۱ به آخر خط رسیده
است و دانش آموزان امید دارند به محض رسیدن او به یکی از برگهایی از نقشهی مدرسه که
یکی از کاراکترهای کمکی در آن حضور داشته باشد زندگی نامبارک او را به پایان
رسانند.
اگر بدانیم در صورت رسیدن کاراکتر
اصلی ۱ به برگهایی که کاراکتری کمکی در آن کمین کرده است، حتما کاراکتر
اصلی ۱ خواهد مرد و در صورت رسیدن به برگی که کسی در آن کمین نکرده است، میتواند
از مدرسه فرار کند و حتما زنده خواهد ماند، بگویید احتمال زنده ماندن کاراکتر اصلی
چقدر است؟
*قطعی برق کاراکتر
اصلی ۱ را در هر مرحله ی جابجایی مجبور به انتخاب تصادفی یکی از رئوس مجاور راسِ
هر مرحله میکند.
*ترس شدید و عذاب
وجدان، کاراکتر اصلی ۱ را مجبور کرده مدام در حال جابجایی در مدرسه باشد تا بمیرد
یا به حالتی برسد که ترس از مرگ نداشته باشد.
# ورودی
در خط اول ورودی به ترتیب دو عدد طبیعی $n$ و $k$ داده میشوند.
در خط دوم ورودی $k$ عدد طبیعی که نشاندهندهی شمارهی رئوسی از درخت که کاراکترهای کمکی در آن کمین کردهاند، است، داده میشود. (تضمین میشود تمامی شماره راسهای داده شده در این خط نشاندهندهی برگهایی از درخت هستند.)
در $n - 1$ خط بعد در هر خط دو عدد طبیعی $u$ و $v$ داده میشوند که این دو راس $u$ و $v$ در درخت متصل هستند.
$$2 \leq n \leq 100 \ 000$$
$$1 \leq k \leq n$$
$$1 \leq v,u \leq n$$
# خروجی
در تنها خط خروجی احتمال زنده ماندن کاراکتر اصلی ۱ را با دقت دقیقا ۶ رقم اعشار چاپ کنید.
(برای مثال بجای `0.5`، `0.500000`را و بهجای `0.63710792`، `0.637108` را چاپ کنید.)
# مثال
## نمونه ورودی
```
3 1
2
1 2
1 3
```
## نمونه خروجی
```
0.500000
```
# توضیح
در متن صورت سوال آمده که کاراکتر اصلی ۱ ابتدائا در راس ۱ قرار دارد. از آنجایی که حتما باید حرکت بکند، پس یا به راس ۲ میرود یا به راس ۳. هر دوی این رئوس برگند. در راس ۲ زندگی کاراکتر اصلی ۱ پایان میپذیرد و در راس ۳ نجات پیدا میکند، پس به احتمال $\frac {1} {2} = 0.5 = 0.500000$ کاراکتر اصلی ۱ زنده میماند.

شهریور خونین
+ محدودیت زمان: ۲ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
*****

در پایان شهریور خونین بالاخره
تکلیف کاراکتر اصلی ۱ روشن شد و او چشم از جهان بست تا دیگر کسی نتواند کاراکترهای
کمکی بی گناه را اذیت کند. اما از آنجایی که داستان این کانتست بسیار غم انگیز میشود
اگر کاراکتر اصلی ۱ تنها و بیکس و در میان انبوهی از کاراکترهای کمکی بمیرد، پس
یک کاراکتر اصلی ۰ای پیدا میشود که از قضا در زمانی که کاراکتر اصلی ۱ خودش هم
کاراکتر کمکی بوده، معلمش بوده است. در این لحظات آخر زندگی برای کاراکتر اصلی ۱، کاراکتر
اصلی ۰ سر او را روی پاهایش میگذارد و میخواهد کاری کند که او در هنگام مرگش با
رضایت و شادکامی از دنیا برود، به همین دلیل در $q$ ثانیهی آخر زندگی کاراکتر اصلی ۱، $q$ سوال از او
میپرسد:
سوال او بیربط به فضای اطراف
آنها در این لحظات نیست، درختی در حیاط مدرسه وجود دارد که رئوسش شمارهگذاری شدهاند و ریشهدار است و ریشهی آن راس ۱ است. کاراکتر
اصلی ۰ در هر ثانیه شمارهی دوتا از رئوس این درخت را به کاراکتر اصلی ۱ میدهد و
چون در لحظات مرگ کمی از بنیهی علمی و توان کاراکتر اصلی ۱ کم شده است تضمین میکند
که راس دومی که داده است حتما در زیردرخت راس اول است. به عبارت دیگر $ v$ و $u$ را میدهد که $ u$ در زیردرخت $v$ است. چیزی که کاراکتر اصلی ۱ باید بگوید این
است که طول بزرگترین مسیر در زیردرخت $v$
با شروع از $u$ چقدر است به عبارت دیگر اگر بقیهی درخت به غیر از زیردرخت راس $v$ حذف شود، بلندترین مسیری که یک راس آن $u$ باشد چه طولی دارد.
کاراکتر اصلی ۱ دانا که تمام
این اتفاقات را از قبل پیش بینی میکرده است دستگاهی ساخته و با خود همراه دارد که
جواب تمام این سوالات کاراکتر اصلی ۰ را بدهد تا او فکر کند که کاراکتر اصلی ۱ با
شادی از دنیا رفته است.
برنامهای بنویسید که مانند
دستگاه کاراکتر اصلی ۱ عمل کند و به سوالات کاراکتر اصلی ۰ پاسخ دهد.
# ورودی
در خط اول ورودی دو عدد طبیعی $n$ و $q$ داده میشوند.
در خط بعدی $n - 1$ عدد که $i$امین عدد نشاندهندهی شمارهی راس پدر راس $i + 1$ است.
در $q$ خط بعدی $q$ پرسش مطرح میشوند، در هر خط دو عدد $v$ و $u$ را میدهد.
$$1 \leq n \leq 100 \ 000$$
$$1 \leq q \leq 100 \ 000$$
$$1 \leq v, u \leq n$$
# خروجی
در $q$ خط پاسخ $q$ پرسش مطرح شده را بدهید.
# مثال
## ورودی نمونه
```
7 3
1 1 2 2 3 3
1 5
2 5
7 7
```
## خروجی نمونه
```
4
2
0
```
# توضیح
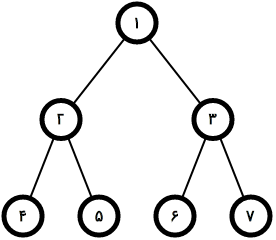
در ثانیهی اول، کاراکتر اصلی ۱ باید بلندترین مسیر با شروع از راس ۵ در کل درخت رو بگوید (زیردرخت ریشه، کل درخت را شامل میشود) که بلندترین مسیر با شروع از راس ۵، مسیر ۵ ۲ ۱ ۳ ۶ یا ۵ ۲ ۱ ۳ ۷ می باشند که طولشان ۴ است.
در ثانیهی دوم، کاراکتر اصلی ۱ باید بلندترین مسیر با شروع از راس ۵ در زیردرخت راس ۲ (شامل رئوس ۲، ۴ و ۵) را بگوید، که مسیر ۵ ۲ ۴ و به طول ۲ است.
در ثانیهی سوم، کاراکتر اصلی ۱ باید بلندترین مسیر با شروع از راس ۷ در زیردرخت خود راس ۷ را بگوید. چون راس ۷ برگ است و زیردرخت راس ۷ فقط شامل خودش است، پس طول بلندترین مسیر در آن ۰ است.
ثانیههای آخر
+ محدودیت زمان: ۲ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
*****

سالها از مرگ دردناک و مظلومانهی کاراکتر اصلی ۱ گذشت، در متن وصیتنامهی آن مرحوم آمده بود که دوست دارم پسرم هم کاراکتر اصلی بشود و نه یک کاراکتر کمکی.
پسرِ کاراکتر اصلی ۱ نیز مثل کاراکترهای کمکیِ شاگرد پدرش از هندسه متنفر بود اما بهشدت به درس شیمی علاقهمند بود، به همین علت مدرس درس شیمی در دانشگاه شد و کاراکتر اصلی ۲ نام گرفت. از قضا شاگردان پدرش نیز در دانشگاه، شدند شاگردان او در درس شیمی!
دانشگاهها بهتازگی آغاز به کار کردهاند و کاراکتر اصلی ۲ میخواهد در همین ترم اول دانشگاه انتقام پدرش را بگیرد و با کاراکترهای کمکی بیحساب بشود پس آنچنان سوال سختی برای امتحان شیمی آنها طرح کرده که روح پدرش به آرامش برسد! سوال این است:
تعداد $n$ اتم داریم (شمارهگذاری شده از ۱ تا $n$) که بعضی از آنها باهم پیوند دادهاند، میدانیم هر پیوند فقط بین ۲ اتم شکل میگیرد. همچنین دربارهی اتمهای داده شده میدانیم فقط ۲ نوع پیوند میان این اتمها ممکن است، پیوندهای شُل و پیوندهای سفت.
در ابتدا همهی پیوندها از نوع شُل هستند. وسیلهای داریم که قادر است نوع پیوند میان دو اتم را از شُل به سفت تغییر دهد. از دیگر قابلیتهای این وسیله، نمایشگری است که اندازهی بزرگترین **زیرمجموعهی خفن** از مجموعهای از اتمها که به آن دادیم را پس از هربار عمل سفتسازی (تغییر پیوند میان دو اتم از شل به سفت) نشان میدهد.
**زیرمجموعهی خفن** یعنی زیرمجموعهای از اتمها که بین هر دو اتم از این زیرمجموعه رابطهی **طلایی** وجود **نداشته** باشد.
همانطور که میدانید الکترونها میتوانند با استفاده از پیوند بین دو اتم بین این دو اتم جابجا شوند.
دو اتم رابطهی **طلایی** دارند اگر و تنها اگر یک الکترون بتواند با جابجایی بین اتمها با استفاده از پیوندهای بینشان از یکی به آنیکی برسد طوری که از هیچ پیوندی دوبار استفاده نکند و حداقل از یک پیوندِ سفت، استفاده کند. (دقت کنید ممکن است الکترون چند بار از یک اتم استفاده کند اما چندبار از یک پیوند استفاده نمیکند)
مدتی است نمایشگر وسیله خراب شده است به همین دلیل جزئیات اعمال سفتسازی (تغییر پیوند میان دو اتم از شل به سفت) انجام شده را در اختیار شما قرار میدهیم و شما باید اندازهی بزرگترین **زیرمجموعهی خفن** از مجموعهی داده شده اتم را پس از هربار عمل سفتسازی محاسبه کنید.
از آنجایی که هیچکدام از کاراکترهای کمکی در امتحان قادر به حل این سوال نیستند. کاراکتر اصلی ۲ در جهت آرامش بیشتر پدرش تصمیم گرفت این سوال را برای تیم طراحی سوالات این مسابقه ارسال کند تا ما آن را در بین سوالاتمان قرار دهیم. حال برنامهای بنویسید که با محاسبهی درست پاسخ آرامش را از روح کاراکتر اصلی ۱ بگیرد.
# ورودی
در خط اول ورودی سه عدد طبیعی $n$، $m$ و $q$ به ترتیب نشاندهندهی تعداد اتمها، تعداد پیوندها و تعداد دفعات انجام عمل سفتسازی، داده میشوند.
در $m$ خط بعدی و در هر خط دو عدد طبیعی $v$ و $u$ داده میشوند که شمارهی دوتا از اتمها هستند که میان آنها یک پیوند وجود دارد. (پیوندها به ترتیب داده شدن از ۱ تا $m$ شمارهگذاری شده اند.)
در $q$ خط بعدی و در هر خط یک عدد طبیعی داده میشود که شمارهی پیوندی است که دستگاه روی آن عمل سفتسازی انجام میدهد. تضمین میشود قبل از این هیچگاه روی این پیوند عمل سفتسازی انجام نشده است.
$$1 \leq n, m, q \leq 100 \ 000$$
$$1 \leq v, u \leq n$$
# خروجی
در $q$ خط اندازهی بزرگترین **زیرمجموعهی خفن** را پس از $q$ بار انجام عمل سفتسازی چاپ کنید.
# مثال
## ورودی نمونه
```
4 4 1
1 2
2 3
3 1
3 4
1
```
## خروجی نمونه
```
1
```
# توضیح
پس از آنکه پیوند بین دو اتم ۱ و ۲ سفت میشود، از بین چهار اتم ۱ و ۲ و ۳ و ۴، بین هر دوتایی رابطه طلایی یافت میشود؛ بنابراین از بین این چهار اتم حداکثر یک اتم میتواند در مجموعه خفن باشد.
