| اگر تا حالا توی کوئرا سوالی حل نکردی این ویدیو رو ببین! |
|:---:|
| %video.arvan_https://player.arvancloud.ir/index.html?config=https://qvideo.arvanvod.ir/Z7LYW3YQBA/7xQM9V4Vk9/origin_config.json% |
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
در این سوال به شما دو عدد صحیح مثل $a$ و $b$ داده میشود. از شما میخواهیم برنامهای بنویسید که مقدار $a$ و $b$ را دریافت کند و $a + b$ را چاپ کند.
# ورودی
در تنها سطر ورودی، دو عدد صحیح $a$ و $b$ که با یک فاصله از هم جدا شدهاند، داده میشود.
$$1 \leq a, b \leq 100$$
# خروجی
در تنها سطر خروجی، مقدار $a + b$ را چاپ کنید.
# مثالها
## ورودی نمونه ۱
```
3 5
```
## خروجی نمونه ۱
```
8
```
## ورودی نمونه ۲
```
1 1
```
## خروجی نمونه ۲
```
2
```
<details class="red">
<summary>
# **اشتباهات متداول**
</summary>
<details class="red">
<summary>
**چک کردن شرایط ورودی مسئله**
</summary>
نیازی نیست چک کنید شرایط گفته شده در ورودی برقرار است یا نه. توضیحات محدودیتها فقط برای آگاهی شما دربارهی تستها و محدودیتهای مسئله است و قطعاً در ورودیهای داده شده به برنامهی شما رعایت میشوند. پس نیازی نیست بنویسید:
```python
if 1 <= n <= 100:
# answer of problem
else:
# print('invalid input')
```
</details>
<details class="red">
<summary>
**ابتدا همهی ورودی را گرفتن و در نهایت همهی خروجی را چاپ کردن**
</summary>
شما میتوانید لابهلای دریافت ورودی، خروجی دهید. پس نیازی نیست ابتدا همهی ورودیها را دریافت کنید و در نهایت همهی خروجیها را چاپ کنید. مخصوصاً برای سوالاتی که باید به چندین سوال پاسخ دهید، میتوانید دو قسمت ورودی و خروجی را کاملاً مستقل در نظر بگیرید و مطمئن باشید تداخلی پیش نمیآید.
</details>
<details class="red">
<summary>
**چاپ کردن موارد اضافه برای دریافت ورودی**
</summary>
لطفاً از چاپ کردن موارد اضافه مثل `please enter a number` برای دریافت ورودی پرهیز کنید. برای مثال در زبان پایتون نباید بنویسید:
```python
input('please enter:')
```
</details>
<details class="red">
<summary>
**چند فایلی کد زدن**
</summary>
برای زبانهایی مثل جاوا نباید در بالای کد شما آدرس پکیج داده شود. برای مثال در بالای کد خود نباید بنویسید:
```java
package ir.quera.contest;
```
</details>
<details class="red">
<summary>
**استفاده از چند `Scanner` برای دریافت ورودی**
</summary>
در زبان جاوا، باید فقط یک شئ از جنس `Scanner` تعریف کنید و همهی ورودیها را با آن دریافت کنید.
</details>
<details class="red">
<summary>
**نحوهی دریافت ورودی و چاپ کردن خروجی**
</summary>
برای آشنایی بیشتر برای نحوهی دریافت ورودی و چاپ کردن خروجی این [لینک](https://quera.org/course/assignments/2693/problems/8774) را مطالعه کنید.
</details>
جمع دو عدد (آموزشی)
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
پس از تغییرات شدید جو و دما در کره زمین، محمد شروع به بررسی دما در کشور های مختلف کرد. در هر کشور، تعداد روزهای سال متفاوت است. اگر در یک کشور هر فصل $k$ روز داشته باشد.کل سال از
$4 \times k$
روز تشکیل شده. میدانیم هر کشور دمای روزهای کل سال به صورت چرخشی ثابت است. به این شکل که دمای یک روز با دما $4 \times k$ روز بعد یکسان است.
علی طی یک تحقیقات دما
$4 \times k$
روز متوالی را بررسی کرده و به شما میدهد. توجه کنید که او لزوما از روز سال بهار شروع به جمع آوری دادهها نکرده است.
فصل های هر کشور **به ترتیب** بهار، تابستان، پاییز و زمستان است.
علی به یک تابستان جهنمی میگوید اگر مجموع دما آن تابستان کمتر از مجموع دمای هیچ $k$ روز متوالی دیگری در سال نباشد.
او به یک زمستان یخبندان میگوید اگر مجموع دما در آن فصل بیشتر از مجموع دمای هر $k$ روز متوالی دیگری در سال نباشد.
از دید محمد کشوری چهار فصل است که تابستان آن جهنمی و زمستان آن یخبندان باشد. حال شما باید به ازای $T$ کشور دنبالهی دمای آن به ازای
$4 \times k$
دریافت کرده و بگویید که آیا ممکن است این لیست دمای روزهای متوالی یک کشور چهارفصل باشد یا خیر.
# ورودی
در خط اول ورودی عدد $T$ که نشان دهنده تعداد کشور ها است آمده است.
سپس به زای هر کشور دو خط ورودی داده میشود که در خط اول $k_i$ یا همان طول یک فصل کشور $i$م امده است. در خط بعدی $k_i * 4$ عدد
$a_j$
آمده که نشان دهنده $j$م عضو لیست دمای آن کشور است.
# خروجی
به ازای هر کشور اگر آن کشور میتوانست چهارفصل باشد Yes و در غیر اینطورت No چاپ کنید.
# محدودیتها
$$1 \leq T \leq 5*10^4$$
$$1 \leq k_i \leq 5*10^4$$
$$-10^9 \leq a_j \leq 10^9$$
$$1 \leq \sum k_i \leq 5*10^4$$
# مثالها
### ورودی نمونه اول
```
3
1
1 2 3 4
1
1 3 4 2
2
1 2 3 4 4 3 2 1
```
### خروجی نمونه اول
```
No
Yes
Yes
```
در کشور اول، دمای تابستان جهنمی ۴ و دمای زمستان یخبندان باید ۱ باشد. ولی روشی برای پیدا کردن تابستان جهنمی و زمستان یخبندان نداریم به طوری که بین آنها فاصله دقیقا $k$ روزی داشته باشیم که فصل پاییز و بهار را تشکیل دهد.
در کشور دوم، دمای تابستان جهنمی ۴ و دمای زمستان یخبندان ۱ است. اگر دمای دوم را شروع سال در نظر بگیریم مجموع دمای تابستان ۱ و مجموع دمای زمستان 4 میشود که به ترتیب جهنمی و یخبندان است.
در مثال سوم اگر دمای دوم را شروع فصل بگیریم، خواسته سوال برقرار میشود.
زمستان
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
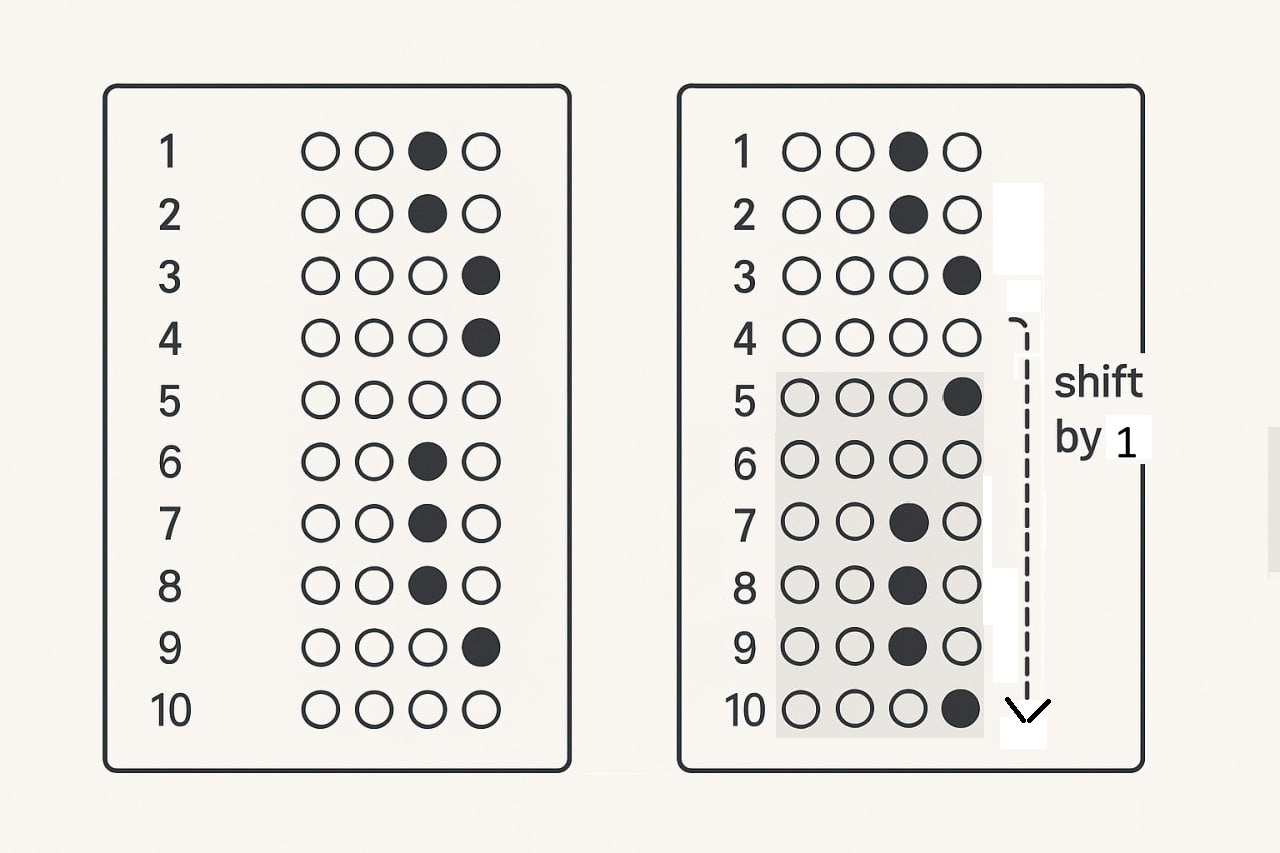
پارسا میخواهد در آزمون مرحله یک المپیاد شرکت کند. او در آزمونها به استراتژی ثابتی پایبند است: سؤالها را به ترتیب از $1$ تا $n$ بررسی میکند، هر سؤالی که حل شود را همانجا علامت میزند و به سؤال بعدی میرود. او هرگز به عقب برنمیگردد و هیچ سؤالی را دوبار پاسخ نمیدهد. در یک آزمون تمرینی، پارسا برخی سؤالها را نتوانسته حل کند و آنها را خالی گذاشته است.
او در کل به $m$ سوال در پاسخبرگ پاسخ داده است. $i$-امین سوالی که به آن پاسخ داده است، سوال $p_i$ است که برای آن گزینهی $c_i$ را در پاسخبرگ وارد کرده است.
پارسا گمان میکند **حداکثر یکبار در وارد کردن شماره سؤالها روی پاسخبرگ اشتباه کرده است**. تعریف دقیق یکبار اشتباه چنین است: در یک **بازه متوالی** از پاسخ ها برای سوالات، برای هر سوال شماره سؤالی که پارسا برای آن پاسخ را ثبت کرده به اندازه عدد صحیح غیرصفر $d$ جابهجا شده است؛ یعنی پاسخهای آن بازه بهجای سؤالهای $\{p_\ell,\dots,p_r\}$ روی سؤالهای $\{p_\ell+d,\dots,p_r+d\}$ ثبت شدهاند (یا برعکس، معادل با اینکه «سؤالات مقصود» او در آن بازه $\{p_i-d\}$ بودهاند). خارج از این بازه، هیچ جابهجایی رخ نداده است. این اشتباه بیش از یکبار رخ نداده یا ممکن است اصلاً رخ نداده باشد.
توجه کنید که پارسا پاسخها را **به ترتیب** و بدون تکرار وارد کرده است؛ بنابراین دنباله «سؤالات پاسخ داده شده» باید صعودی و در بازهٔ $[1..n]$ باشد و هیچ سؤالی دوبار پاسخ داده نشده باشد.
شما پاسخ برگ را دارید و معلوم نیست که کجا و به چه شکلی اشتباه انجام شده. هدف شما این است که با فرض امکان وقوع «حداکثر یکبار اشتباه» به شکل فوق، **بیشترین نمره ای که پارسا با درست وارد کردن سوالات میتوانست بدست بیاورد**(تعداد پاسخهای درست نسبت به کلید آزمون) را محاسبه کنید.
# ورودی
در خط اول ورودی عدد $T$ (تعداد تستها) آمده است. سپس برای هر تست:
- خط اول شامل دو عدد صحیح $n$ و $m$ است؛ بهترتیب تعداد کل سؤالها و تعداد سؤالهایی که پارسا پاسخی برای آنها وارد کرده است.
- خط دوم رشتهای $S$ با طول $n$ شامل حروف `A` تا `E` است که کلید صحیح آزمون را نشان میدهد؛ $S[i]$ پاسخ صحیح سؤال $i$ام است.
- سپس $m$ خط میآید؛ در هر خط یک عدد صحیح $p_i$ $(1 \le p_i \le n)$ و یک حرف $c_i \in \{A,B,C,D,E\}$ آمده است. اینها بیان میکنند پارسا روی پاسخبرگ برای سؤال $p_i$ گزینهٔ $c_i$ را علامت زده است.
- تضمین میشود $p_1 < p_2 < \dots < p_m\ $.
# خروجی
برای هر تست، یک خط شامل یک عدد چاپ کنید: بیشترین تعداد پاسخهای درست که میتوان برای پارسا فرض کرد.
# محدودیتها
$$
1 \le T \le 10^4
$$
$$
1 \le n \le 5000,\quad 0 \le m \le n
$$
$$
\sum n \le 5000
$$
# مثالها
## ورودی نمونه ۱
```
4
5 4
AECDB
1 A
2 A
4 C
5 B
7 2
AAACDAA
1 C
3 D
7 2
AAACDAA
1 C
2 D
10 5
ABECCDBAEA
3 B
4 E
6 C
8 A
10 E
````
## خروجی نمونه ۱
```
3
1
2
4
````
مرحله یکی گیج
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
---------
مسابقات گرند پردیس فرمول یک برگزار شده است. در این مسابقه
$n\ $
نفر شرکت کردهاند که هر کدام متعلق به یک تیمی هستند. رتبه بندی نهایی بازیکنان مشخص شده است. آشمز نمیداند در این لیست رتبهبندی هر بازیکن در کدام تیم است اما به ازای هر بازیکن با رتبه
$1 \le i \le n\ $
میداند تعداد بازیکنهایی که تیمشان با این بازیکن یکسان است و رتبه کمتری دارند
$a_i\ $
تاست و تعداد بازیکنهایی که تیمشان با این بازیکن یکسان است و رتبه بالاتری دارند
$b_i\ $
تاست. آشمز میخواهد بداند با توجه به اعداد گفته شده تیمبندی بازیکن ها چند حالت دارد. اما او که از شمردن خسته شده است، از شما میخواهد برنامهای بنویسید تا این مقدار را محاسبه کند.
شما باید تعداد دنبالههای
$c_1, c_2, \ldots, c_n\ $
را بشمارید که به ازای هر
$1 \le i \le n\ $
داشته باشیم
$1 \le c_i \le n\ $
و تعداد
$j\ $
هایی که
$1 \le j < i\ $
و
$c_i = c_j\ $
برقرار باشند،
$a_i\ $
تا باشد، و تعداد
$j\ $
هایی که
$i < j \le n\ $
و
$c_i = c_j\ $
برقرار باشند،
$b_i\ $
تا باشد. باقی ماندهی جواب را به پیمانهی
$998244353\ $
محاسبه کنید.
# ورودی
در خط اول ورودی عدد $T$ تعداد سناریو ها میآید.
در خط اول هر سناریو عدد
$n_i$
که نشاندهندهی تعداد بازیکنها در سناریو $i$ام است میآید.
در خط دوم هر سناریو دنبالهی
$a_1, a_2, \ldots, a_n\ $
و در خط سوم هر سناریو دنبالهی
$b_1, b_2, \ldots, b_n\ $
میآید.
تضمین میشود به ازای سناریو حداقل یک دنبالهی معتبر وجود دارد ( جواب 0 نمیشود )
$$1 \le T \le 10^4$$
$$1 \le n_i \le 2 \cdot 10^5$$
$$0 \le a_i, b_i < n$$
$$1 \leq \sum n_i \leq 2 \cdot 10^5$$
# خروجی
برای هر سناریو در یک خط تعداد حالات دنبالهی
$c_1, c_2, \ldots, c_n\ $
را به پیمانهی
$998244353\ $
خروجی دهید.
# مثال
## ورودی نمونه ۱
```
5
1
0
0
3
0 1 2
2 1 0
5
0 1 0 1 2
1 0 2 1 0
5
0 0 0 1 1
0 1 1 0 0
10
0 0 1 2 0 1 1 0 2 3
3 2 2 1 1 1 0 0 0 0
```
## خروجی نمونه ۱
```
1
3
20
120
5040
```
در سناریوی اول تنها دنبالهی معتبر
$[1]$
میباشد.
در سناریوی دوم تمام اعضای دنباله باید برابر یکی از اعداد 1 یا 2 یا 3 باشند که 3 حالت دارد.
در سناریوی سوم یکی در دنبالههای معتبر
$[1, 1, 2, 2, 2]$
میباشد.
گرند پردیس
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
پوریا در حال ساختن پایگاه خودش در بازی **Terraria** است. پایگاه او زیر زمین است و نقشهی زمین بالای پایگاه به شکل یک جدول با $n$ سطر و $m$ ستون داده شده که هر خانه یا خالی (`.`) است یا مانع (`#`).
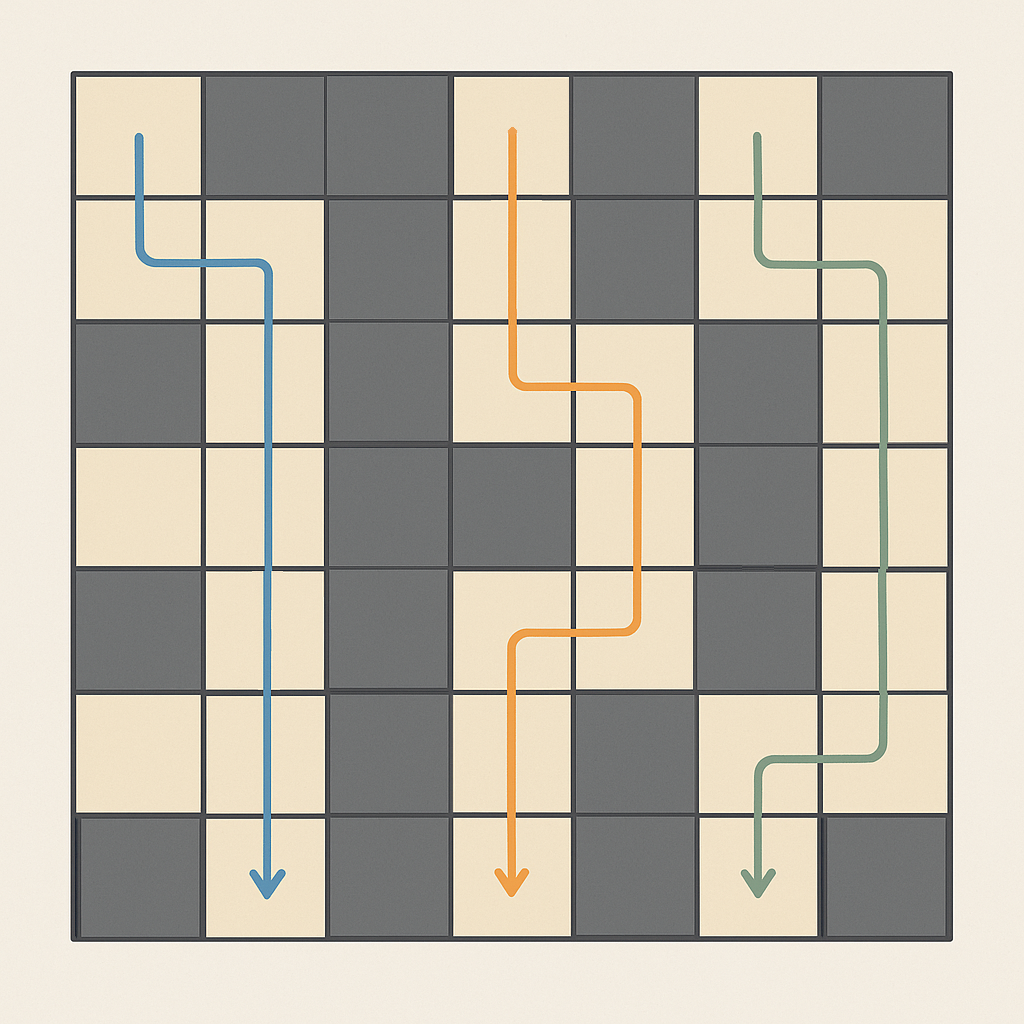
پوریا میخواهد از بالای نقشه به پایین آن یک مسیر بسازد. مسیر باید در یکی از خانههای خالی سطر اول شروع شود و در یکی از خانههای خالی سطر آخر تمام شود. با شروع از خانه ای در سطر اول در هر مرحله میتوان از یک خانه به یک خانهی مجاور ضلعی اش حرکت کرد در صورتی که حرکت به جهت **پایین**، **چپ** یا **راست** باشد و از جدول خارج نشویم. حرکت رو به بالا مجاز نیست چون پوریا بر این باور است که برای رسیدن به پایگاه اتلاف انرژیست. همچنین مسیر نمیتواند از داخل مانع (`#`) یا خانهای تکراری عبور کند.
به این ترتیب، ممکن است چند مسیر مختلف از بالا به پایین وجود داشته باشد. ما «پیچیدگی» نقشه را برابر با تعداد این مسیرها تعریف میکنیم. پوریا دوست دارد نقشهاش پیچیدگی دقیقاً برابر با **۱** داشته باشد: یعنی دقیقاً یک مسیر یکتا از بالا به پایین وجود داشته باشد.
وظیفهی شما این است که برای **هر خانه** بررسی کنید اگر مقدار آن خانه را برعکس کنیم (یعنی `.` را به `#` یا `#` را به `.` تغییر دهیم) آیا پیچیدگی جدول جدید دقیقاً برابر با ۱ میشود یا نه.
# ورودی
خط اوّل شامل یک عدد صحیح $t$ است — تعداد تستها.
$$ 1 \leq t \leq 10^5 $$
خط اول هر تست شامل دو عدد صحیح $n$ و $m$ است — تعداد سطرها و ستونهای جدول.
$$ 1 \le n, m \le 10^6,\; n \cdot m \le 10^6 $$
سپس \(n\) خط میآید که هرکدام دقیقاً شامل \(m\) کاراکتر `.` یا `#` است و وضعیت جدول را توصیف میکند.
تضمین میشود که مجموع \(n \cdot m\) روی تمام تستها از \(10^6\) بیشتر نمیشود.
# خروجی
برای هر تست یک جدول $n \times m$ چاپ کنید. در سطر $i$ از خروجی، باید دقیقاً $m$ کاراکتر بدون فاصله چاپ شود.
کاراکتر مربوط به خانهی $(i,\ j)$ باید `1` باشد اگر با تغییر همان خانه پیچیدگی دقیقاً برابر با ۱ میشود، و `0` در غیر این صورت.
# مثال
## ورودی نمونه ۱
```
3
4 4
##.#
...#
.#.#
.#.#
5 5
##.##
...##
.##..
..##.
#.###
3 1
.
#
.
````
## خروجی نمونه ۱
```
0000
1100
1010
1010
00001
00011
00111
00111
00011
0
1
0
````
تراریا
+ محدودیت زمان: ۲ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
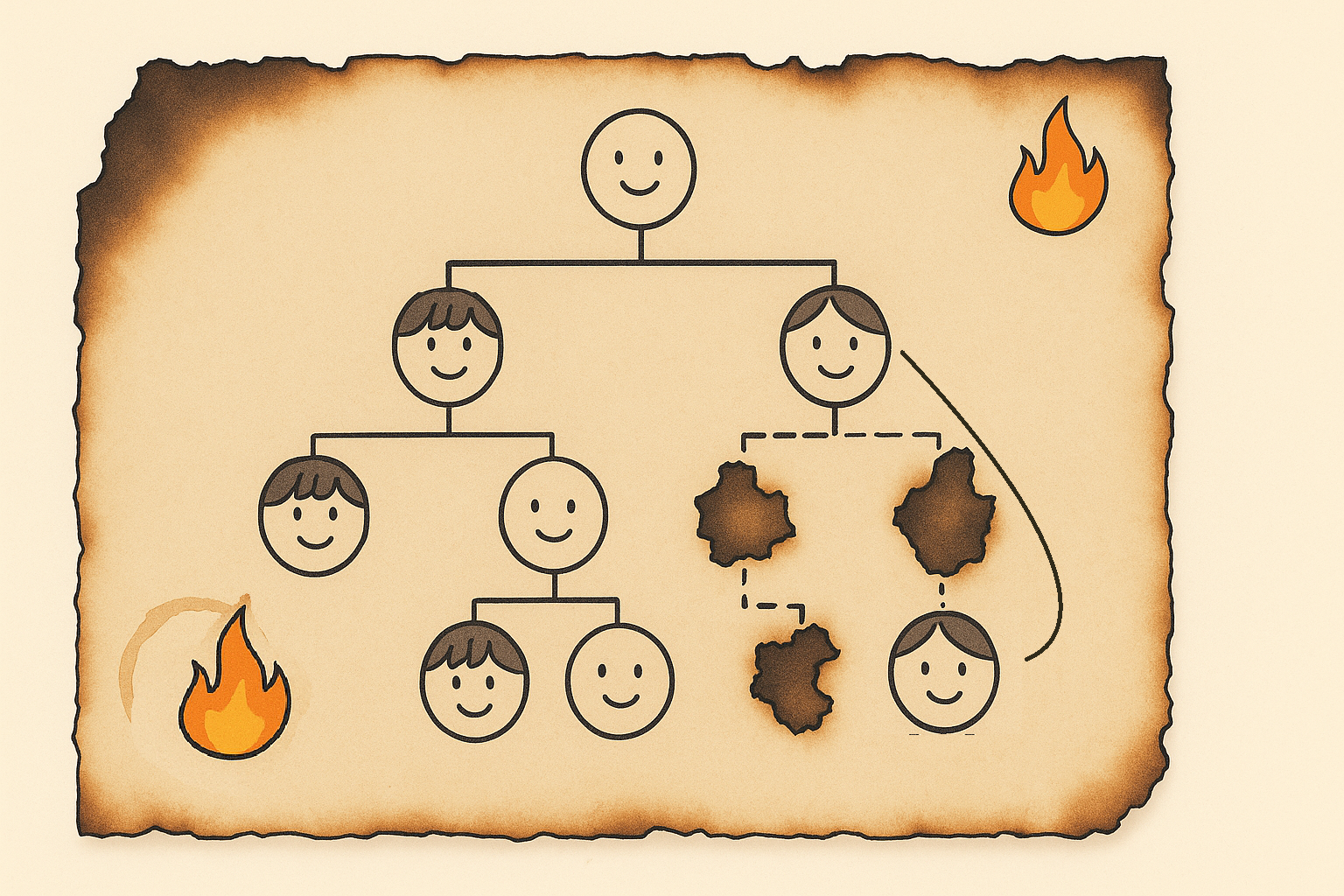
خانواده قدیمی پردیس شجرهنامه طویلی داشته که سوخته است. از آنجایی که این خانواده بسیار بزرگ بوده هیچکس ارتباطات را به طور کامل به یاد ندارد.
در یک مهمانی $n$ نفر از اعضای خانواده به منظور بازسازی شجره نامه دورهم گرد آمدهاند. هر نفر با دیدن افراد، مقداری از روابط بین افراد مهمانی در شجره را به یاد میآورد. هر گفته یکی از دو نوع زیر است
+ فرد $x$ پدر فرد $y$ است.
+ فرد $x$ پدربزرگ فرد $y$ است.
هر دو فرد $x$ و $y$ در مهمانی حضور دارند.
دقت کنید ممکن است همه افراد خانواده در مهمانی حضور نداشته ولی در اطلاعات بیانشده هر دو فرد در مهمانی حضور دارند.
اطلاعات ممکن است تکراری و یا بعضاً غیر کاربردی باشند. اما **همیشه درست** اند. و تضمین شده که حداقل یک درختِ ریشهدار (شجرهنامه) وجود دارد که همهٔ گفتهها در آن برقرارند.
همچنین دادهها بهگونهای هستند که از هر فردی در مهمانی با استفاده از ارتباطات گفتهشده میتوان به هر فرد دیگری در مهمانی رسید.
در آخر بعد از جمعآوری تمام داده ها، پیر پردیس وارد میشود. به خاطر ابهت او، هیچکسی نمیتواند قضیه سوختن شجرهنامه را لو بدهد. پیرِ پردیس چند سؤال میپرسد و اعضای پردیس باید به بهترین شکل پاسخ دهند. در هر سؤال نام دو نفر از اعضای مهمانی $s$ و $t$ را میدهد و میپرسد «فاصلهٔ این دو نفر در شجرهنامهٔ اصلی چقدر است؟»
از آنجا که شجرهنامهٔ اصلیِ دقیق معلوم نیست، شما باید با توجه به اطلاعات موجود، برای هر سؤال کمترین و بیشترین فاصلهای را که s و t **ممکن است** در بین همهٔ درختهای سازگار داشته باشند محاسبه کنید تا پردیسها از بین این دو عدد حدس درستی بزنند و به پیر پردیس بدهند.
# ورودی
در سطر اول عدد صحیح $n$ میآید که تعداد پردیسها در درخت شجرهنامه را نشان میدهد.
در سطر دوم $n$ رشته **متفاوت** میآیند که نام افراد در خانواده حاضر در مهمانی را نشان میدهند. (طول هر اسم ≤ `20`).
در سطر سوم عدد صحیح $m$ میآید که تعداد دادههای موجود که اعضای خانواده به یاد میآورند را نشان میدهد.
در هر یک از $m$ سطر بعدی، یک داده به یکی از دو صورت زیر میآید:
+ $x \text{ pedarbozorg } y$
+ $x \text{ pedar } y$
در سطر بعدی عدد صحیح $q$ میآید که تعداد سوالات پیر پردیس را نشان میدهد.
در هر یک از $q$ سطر بعدی دو رشته $s$ و $t$ میآید که سوالات پیر پردیس را نشان میدهند.
$$ 1 \le n, m, q \le 10^5$$
$$1 \leq |s|, |t| \le 20$$
تضمین میشود که گفتههای پردیسها و نامهای افراد معتبرند و حداقل یک درخت ریشهدار وجود دارد که شرایط همه گفتهها را داشتهباشد.
# خروجی
در $q$ سطر بهترتیب برای هر سوال پیر پردیس، دو عدد چاپ کنید که اولین عدد کمترین فاصلهای که این دو نفر میتوانند در بین درختهای ممکن داشته باشند و دومین عدد بیشترین فاصلهای که میتوانند داشته باشند است.
# مثالها
## ورودی نمونه ۱
```
3
eyd norooz baastaani
2
baastaani pedarbozorg norooz
baastaani pedarbozorg eyd
1
eyd norooz
````
## خروجی نمونه ۱
```
2 4
````
گفتهها میگویند `baastaani` پدر بزرگ هر دوِ `khame` و `shir` است. حال در ماکسیمم حالت پدر هیچ کدام از آنها در مهمانی حضور ندارد که با مسیر چهار در درخت خانوادگی میتوانند به هم برسد. یا با هم دیگر برادرند که در این صورت فاصله آنها دو است. در این مثال در هر صورت پدر این دو نفر نمیتواند در مهمانی حضور داشته باشد.
## ورودی نمونه ۲
```
10
ali sabze amin sib romina seke senjed mahi samanoo abol
9
amin pedar mahi
abol pedarbozorg mahi
romina pedar samanoo
romina pedarbozorg ali
sabze pedar ali
mahi pedarbozorg sib
seke pedarbozorg samanoo
romina pedar senjed
amin pedarbozorg seke
6
romina sib
seke sabze
ali amin
amin sib
seke sib
abol ali
````
## خروجی نمونه ۲
```
2 6
2 2
5 5
3 3
1 5
6 6
````