• محدودیت زمان: ۲ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

دو آرایه به طول $2n$ داریم که هر یک از اعداد $1$ تا $n$ دقیقاً دو بار در هر آرایه ظاهر شده‌اند. می‌خواهیم آرایه‌ی اول $a_1, a_2, \ldots , a_{2n}$ را به آرایه‌ی دوم $b_1, b_2, \ldots , b_{2n}$ تبدیل کنیم. در هر مرحله می‌توانیم یک بار عملیات $CopyPaste$ را انجام بدهیم.

$CopyPaste(i, j):\ a_i\ =\ a_j$

در این سوال شما باید دنباله‌ای از عملیات‌های $CopyPaste$ ارائه کنید که آرایه اول را به آرایه دوم تبدیل کند. نمره شما بر حسب تعداد عملیات‌هایتان مشخص می‌شود.

ورودی🔗

در خط اول عدد طبیعی $n$ آمده است.

در خط دوم $2n$ عدد طبیعی‌ ‌آمده است که آرایه‌ی $a$ را نشان می‌دهد.

در خط سوم $2n$ عدد طبیعی‌ ‌آمده است که آرایه‌ی $b$ را نشان می‌دهد.

$1 \le n \le 100\ 000$ $1 \le a_i, b_i \le n$

خروجی🔗

در اولین خط خروجی عدد $m$ را چاپ کنید که تعداد عملیات‌های $CopyPaste$ را نشان می‌دهد.

در هر یک از $m$ خط بعدی، به ترتیب دو عدد $i$ و $j$ را چاپ کنید که نشانگر یک عملیات $CopyPaste(i, j)$ است.

زیرمسئله‌ها🔗

الف) شما باید همه‌ی تست‌ها را با کمتر از $4n$ عملیات حل کنید. (۳۰ نمره)

ب) شما باید همه‌ی تست‌ها را با کمتر از $3n$ عملیات حل کنید. (۳۰ نمره)

ج) شما باید همه‌ی تست‌ها را با کمتر از $2n$ عملیات حل کنید. (۴۰ نمره)

مثال🔗

ورودی نمونه ۱🔗

2
1 2 2 1
2 2 1 1

خروجی نمونه ۱🔗

2
1 2
3 4

در این نمونه کمتر از $2n$ عملیات استفاده شده؛ پس این خروجی برای همه‌ی زیرمسئله‌های سوال صحیح است.

ورودی نمونه ۲🔗

2
1 1 2 2
2 2 1 1

خروجی نمونه ۲🔗

4
3 2
1 4
2 4
4 3

در این نمونه از $2n$ عملیات استفاده شده؛ پس این خروجی برای همه‌ی زیرمسئله‌های سوال صحیح است.

ورودی نمونه ۳🔗

4
4 4 3 3 2 2 1 1
1 1 2 2 3 3 4 4

خروجی نمونه ۳🔗

16
5 4
3 6
4 6
6 5
7 6
5 8
6 8
8 7
7 1
1 8
2 8
8 7
5 1
1 6
2 6
6 5

در این نمونه از $4n$ عملیات استفاده شده است، درنتیجه تنها برای زیرمسئله‌ی الف صحیح است.

• محدودیت زمان: ۲ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

دو آرایه به طول $2n$ داریم که هر یک از اعداد $1$ تا $n$ دقیقاً دو بار در هر آرایه ظاهر شده‌اند. می‌خواهیم آرایه‌ی اول $a_1, a_2, \ldots , a_{2n}$ را به آرایه‌ی دوم $b_1, b_2, \ldots , b_{2n}$ تبدیل کنیم. در هر مرحله می‌توانیم یک بار عملیات $CopyPaste$ را انجام بدهیم.

$CopyPaste(i, j):\ a_i\ =\ a_j$

در این سوال شما باید دنباله‌ای از عملیات‌های $CopyPaste$ ارائه کنید که آرایه اول را به آرایه دوم تبدیل کند. نمره شما بر حسب تعداد عملیات‌هایتان مشخص می‌شود.

ورودی🔗

در خط اول عدد طبیعی $n$ آمده است.

در خط دوم $2n$ عدد طبیعی‌ ‌آمده است که آرایه‌ی $a$ را نشان می‌دهد.

در خط سوم $2n$ عدد طبیعی‌ ‌آمده است که آرایه‌ی $b$ را نشان می‌دهد.

$1 \le n \le 100\ 000$ $1 \le a_i, b_i \le n$

خروجی🔗

در اولین خط خروجی عدد $m$ را چاپ کنید که تعداد عملیات‌های $CopyPaste$ را نشان می‌دهد.

در هر یک از $m$ خط بعدی، به ترتیب دو عدد $i$ و $j$ را چاپ کنید که نشانگر یک عملیات $CopyPaste(i, j)$ است.

زیرمسئله‌ها🔗

الف) شما باید همه‌ی تست‌ها را با کمتر از $4n$ عملیات حل کنید. (۳۰ نمره)

ب) شما باید همه‌ی تست‌ها را با کمتر از $3n$ عملیات حل کنید. (۳۰ نمره)

ج) شما باید همه‌ی تست‌ها را با کمتر از $2n$ عملیات حل کنید. (۴۰ نمره)

مثال🔗

ورودی نمونه ۱🔗

2
1 2 2 1
2 2 1 1

خروجی نمونه ۱🔗

2
1 2
3 4

در این نمونه کمتر از $2n$ عملیات استفاده شده؛ پس این خروجی برای همه‌ی زیرمسئله‌های سوال صحیح است.

ورودی نمونه ۲🔗

2
1 1 2 2
2 2 1 1

خروجی نمونه ۲🔗

4
3 2
1 4
2 4
4 3

در این نمونه از $2n$ عملیات استفاده شده؛ پس این خروجی برای همه‌ی زیرمسئله‌های سوال صحیح است.

ورودی نمونه ۳🔗

4
4 4 3 3 2 2 1 1
1 1 2 2 3 3 4 4

خروجی نمونه ۳🔗

16
5 4
3 6
4 6
6 5
7 6
5 8
6 8
8 7
7 1
1 8
2 8
8 7
5 1
1 6
2 6
6 5

در این نمونه از $4n$ عملیات استفاده شده است، درنتیجه تنها برای زیرمسئله‌ی الف صحیح است.

• محدودیت زمان: ۲ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

دو آرایه به طول $2n$ داریم که هر یک از اعداد $1$ تا $n$ دقیقاً دو بار در هر آرایه ظاهر شده‌اند. می‌خواهیم آرایه‌ی اول $a_1, a_2, \ldots , a_{2n}$ را به آرایه‌ی دوم $b_1, b_2, \ldots , b_{2n}$ تبدیل کنیم. در هر مرحله می‌توانیم یک بار عملیات $CopyPaste$ را انجام بدهیم.

$CopyPaste(i, j):\ a_i\ =\ a_j$

در این سوال شما باید دنباله‌ای از عملیات‌های $CopyPaste$ ارائه کنید که آرایه اول را به آرایه دوم تبدیل کند. نمره شما بر حسب تعداد عملیات‌هایتان مشخص می‌شود.

ورودی🔗

در خط اول عدد طبیعی $n$ آمده است.

در خط دوم $2n$ عدد طبیعی‌ ‌آمده است که آرایه‌ی $a$ را نشان می‌دهد.

در خط سوم $2n$ عدد طبیعی‌ ‌آمده است که آرایه‌ی $b$ را نشان می‌دهد.

$1 \le n \le 100\ 000$ $1 \le a_i, b_i \le n$

خروجی🔗

در اولین خط خروجی عدد $m$ را چاپ کنید که تعداد عملیات‌های $CopyPaste$ را نشان می‌دهد.

در هر یک از $m$ خط بعدی، به ترتیب دو عدد $i$ و $j$ را چاپ کنید که نشانگر یک عملیات $CopyPaste(i, j)$ است.

زیرمسئله‌ها🔗

الف) شما باید همه‌ی تست‌ها را با کمتر از $4n$ عملیات حل کنید. (۳۰ نمره)

ب) شما باید همه‌ی تست‌ها را با کمتر از $3n$ عملیات حل کنید. (۳۰ نمره)

ج) شما باید همه‌ی تست‌ها را با کمتر از $2n$ عملیات حل کنید. (۴۰ نمره)

مثال🔗

ورودی نمونه ۱🔗

2
1 2 2 1
2 2 1 1

خروجی نمونه ۱🔗

2
1 2
3 4

در این نمونه کمتر از $2n$ عملیات استفاده شده؛ پس این خروجی برای همه‌ی زیرمسئله‌های سوال صحیح است.

ورودی نمونه ۲🔗

2
1 1 2 2
2 2 1 1

خروجی نمونه ۲🔗

4
3 2
1 4
2 4
4 3

در این نمونه از $2n$ عملیات استفاده شده؛ پس این خروجی برای همه‌ی زیرمسئله‌های سوال صحیح است.

ورودی نمونه ۳🔗

4
4 4 3 3 2 2 1 1
1 1 2 2 3 3 4 4

خروجی نمونه ۳🔗

16
5 4
3 6
4 6
6 5
7 6
5 8
6 8
8 7
7 1
1 8
2 8
8 7
5 1
1 6
2 6
6 5

در این نمونه از $4n$ عملیات استفاده شده است، درنتیجه تنها برای زیرمسئله‌ی الف صحیح است.

• محدودیت زمان: ۲ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

توابع $f: \mathbb{N} \rightarrow \{-1, 1\}$ و $g: \mathbb{N} \rightarrow \mathbb{Z}$ به صورت زیر تعریف می‌شوند:

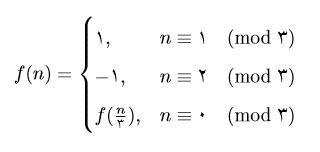
$g(n)=\sum_{i=1}^{n}f(i)$

در توضیحات بالا، منظور از $\mathbb{N}$ مجموعه‌ی اعداد طبیعی و منظور از $\mathbb{Z}$ مجموعه‌ی اعداد صحیح است.

برنامه‌ای بنویسید که $q$ پرسمان به صورت $(l,r)$ دریافت کند و به ازای هر پرسمان تعداد نابجایی‌های دنباله‌ی $g(l), g(l+1), \ldots, g(r)$ را محاسبه کند. با توجه به این‌که پاسخ پرسمان‌ها می‌تواند بزرگ باشد، باقی‌مانده‌ی آن بر $10^9 + 7$ را محاسبه کنید.

تعداد نابجایی‌های دنباله‌ی $a_1, a_2, \ldots, a_n$ برابر است با تعداد جفت $(i,j)$ هایی که $i < j$ و $a_i > a_j$ است.

ورودی🔗

در سطر اول ورودی عدد طبیعی $q$، تعداد پرسمان‌ها، آمده است.

در هر یک از $q$ سطر بعدی به ترتیب دو عدد طبیعی $l$ و $r$ آمده است.

$1\leq q\leq 5\times 10^4$ $1\leq l \leq r\leq 10^{18}$

خروجی🔗

خروجی شامل $q$ سطر است که در $i$ امین $(1\leq i\leq q)$ سطر از آن، پاسخ پرسمان $i$ ام آمده است.

زیرمسئله‌ها🔗

الف) $l,r \leq 10^6$ (۲۵ نمره)

ب) $r - l \leq 100, q \leq 10^4$ (۲۵ نمره)

ج) بدون محدودیت اضافی (۵۰ نمره)

مثال🔗

ورودی نمونه🔗

4
1 1
2 3
1 5
3 17

خروجی نمونه🔗

0
0
2
25

• محدودیت زمان: ۲ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

توابع $f: \mathbb{N} \rightarrow \{-1, 1\}$ و $g: \mathbb{N} \rightarrow \mathbb{Z}$ به صورت زیر تعریف می‌شوند:

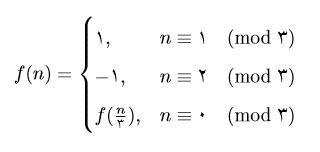
$g(n)=\sum_{i=1}^{n}f(i)$

در توضیحات بالا، منظور از $\mathbb{N}$ مجموعه‌ی اعداد طبیعی و منظور از $\mathbb{Z}$ مجموعه‌ی اعداد صحیح است.

برنامه‌ای بنویسید که $q$ پرسمان به صورت $(l,r)$ دریافت کند و به ازای هر پرسمان تعداد نابجایی‌های دنباله‌ی $g(l), g(l+1), \ldots, g(r)$ را محاسبه کند. با توجه به این‌که پاسخ پرسمان‌ها می‌تواند بزرگ باشد، باقی‌مانده‌ی آن بر $10^9 + 7$ را محاسبه کنید.

تعداد نابجایی‌های دنباله‌ی $a_1, a_2, \ldots, a_n$ برابر است با تعداد جفت $(i,j)$ هایی که $i < j$ و $a_i > a_j$ است.

ورودی🔗

در سطر اول ورودی عدد طبیعی $q$، تعداد پرسمان‌ها، آمده است.

در هر یک از $q$ سطر بعدی به ترتیب دو عدد طبیعی $l$ و $r$ آمده است.

$1\leq q\leq 5\times 10^4$ $1\leq l \leq r\leq 10^{18}$

خروجی🔗

خروجی شامل $q$ سطر است که در $i$ امین $(1\leq i\leq q)$ سطر از آن، پاسخ پرسمان $i$ ام آمده است.

زیرمسئله‌ها🔗

الف) $l,r \leq 10^6$ (۲۵ نمره)

ب) $r - l \leq 100, q \leq 10^4$ (۲۵ نمره)

ج) بدون محدودیت اضافی (۵۰ نمره)

مثال🔗

ورودی نمونه🔗

4
1 1
2 3
1 5
3 17

خروجی نمونه🔗

0
0
2
25

• محدودیت زمان: ۲ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

توابع $f: \mathbb{N} \rightarrow \{-1, 1\}$ و $g: \mathbb{N} \rightarrow \mathbb{Z}$ به صورت زیر تعریف می‌شوند:

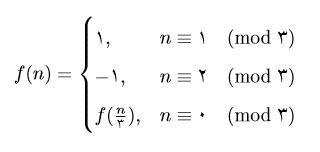
$g(n)=\sum_{i=1}^{n}f(i)$

در توضیحات بالا، منظور از $\mathbb{N}$ مجموعه‌ی اعداد طبیعی و منظور از $\mathbb{Z}$ مجموعه‌ی اعداد صحیح است.

برنامه‌ای بنویسید که $q$ پرسمان به صورت $(l,r)$ دریافت کند و به ازای هر پرسمان تعداد نابجایی‌های دنباله‌ی $g(l), g(l+1), \ldots, g(r)$ را محاسبه کند. با توجه به این‌که پاسخ پرسمان‌ها می‌تواند بزرگ باشد، باقی‌مانده‌ی آن بر $10^9 + 7$ را محاسبه کنید.

تعداد نابجایی‌های دنباله‌ی $a_1, a_2, \ldots, a_n$ برابر است با تعداد جفت $(i,j)$ هایی که $i < j$ و $a_i > a_j$ است.

ورودی🔗

در سطر اول ورودی عدد طبیعی $q$، تعداد پرسمان‌ها، آمده است.

در هر یک از $q$ سطر بعدی به ترتیب دو عدد طبیعی $l$ و $r$ آمده است.

$1\leq q\leq 5\times 10^4$ $1\leq l \leq r\leq 10^{18}$

خروجی🔗

خروجی شامل $q$ سطر است که در $i$ امین $(1\leq i\leq q)$ سطر از آن، پاسخ پرسمان $i$ ام آمده است.

زیرمسئله‌ها🔗

الف) $l,r \leq 10^6$ (۲۵ نمره)

ب) $r - l \leq 100, q \leq 10^4$ (۲۵ نمره)

ج) بدون محدودیت اضافی (۵۰ نمره)

مثال🔗

ورودی نمونه🔗

4
1 1
2 3
1 5
3 17

خروجی نمونه🔗

0
0
2
25

• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

باشگاه هکر‌‌های جوان، مدرسه‌ای برای تربیت هکر‌ها است. در مراسم فارغ‌التحصیلی باشگاه، که به کلاه‌گذاری معروف است، هکر‌ها در یک صف می‌ایستند و بر روی سر هر کدام از آن‌ها یک کلاه می‌گذارند که آینده‌ی آن‌ها را مشخص خواهد کرد. کلا‌ه‌ها سفید یا سیاه هستند. کلاه‌سفید‌ها هدف کمک به جامعه و کلاه‌سیاه‌ها هدف دیگری(؟) دارند.

تعداد فارغ‌التحصیلان امسال $n$ نفر است و در انبار $w$ کلاه سفید و $b$ کلاه سیاه وجود دارد. همه‌ی دانش‌آموختگان نیز از موجودی انبار باخبر هستند. در صف، هر فرد تنها از رنگ کلاه افراد جلویی‌اش با‌خبر است و حتی رنگ کلاه خودش را نمی‌داند. یعنی فردی که در ابتدای صف ایستاده، رنگ کلاه هیچ‌کس را نمی‌داند و فردی که در انتهای صف است، رنگ کلاه همه به جز خودش را می‌داند.

در انتهای مراسم کلاه‌گذاری، افراد یک به یک و از انتهای صف از مراسم خارج می‌شوند. هر فرد قبل از خارج شدنش اگر از رنگ کلاهش مطمئن باشد، رنگ کلاهش را اعلام می‌کند و به عنوان جایزه پیتزا می‌گیرد (گفتنی است که هکر‌ها، علاقه‌ی شدید به پیتزا دارند!). البته به خاطر کمبود بودجه باشگاه، فقط به اولین فردی که رنگ کلاهش را درست تشخیص بدهد، پیتزا می‌دهند. اگر فردی نیز از رنگ کلاهش مطمئن نباشد، بلند و با افتخار اعلام می‌کند که رنگ کلاهش را نمی‌داند تا افراد باقی‌مانده در مراسم (افرادی که در صف جلوی او قرار داشتند) را نیز از نگون‌بختی‌اش مطلع کند.

امیر نفر $i$ ام صف از انتها است. برای نمونه اگر امیر در انتهای صف باشد، $i=1$ است. در چند حالت از کلاه‌گذاری هکر‌ها، امیر صاحب پیتزا می‌شود؟ دو کلاه‌گذاری متفاوت هستند اگر هکری وجود داشته باشد که در یکی از آن‌ها، کلاه‌سفید و در دیگری کلاه‌سیاه باشد. با توجه به این‌که این مقدار می‌تواند بزرگ باشد، باقی‌مانده آن را بر $10^9 + 7$ حساب کنید.

به توضیحات ورودی و خروجی‌های نمونه توجه کنید!

ورودی🔗

در سطر اول ورودی به ترتیب چهار عدد صحیح و نامنفی $b$، تعداد کلاه‌های سیاه، $w$، تعداد کلاه‌های سفید، $n$، تعداد فارغ‌التحصیلان و $i$، مکان امیر نسبت به انتهای صف آمده است. $0\leq b, w, n\leq 2000$ $1\leq i\leq n\leq b + w$

خروجی🔗

در تنها سطر خروجی، پاسخ مسئله را چاپ کنید.

زیرمسئله‌ها🔗

الف) $b,w,n \leq 20$ (۳۰ نمره)

ب) بدون محدودیت اضافی (۷۰ نمره)

ورودی نمونه ۱🔗

1 1 2 1

خروجی نمونه ۱🔗

2

در این نمونه یک کلاه سفید و یک کلاه سیاه موجود است پس رنگ کلاه نفر اول و دوم متفاوت است. وقتی از نفر اول رنگ کلاهش را می‌پرسند با دیدن رنگ کلاه نفر بعد و دانستن اینکه از هر رنگ فقط یک کلاه وجود دارد می‌تواند رنگ کلاه خود را مشخص کند.

ورودی نمونه ۲🔗

1 1 2 2

خروجی نمونه ۲🔗

0

ورودی نمونه ۳🔗

2 1 2 1

خروجی نمونه ۳🔗

1

ورودی نمونه ۴🔗

2 2 3 2

خروجی نمونه ۴🔗

4

در این نمونه یکی از حالت‌های ممکن این است که رنگ کلاه نفر اول و سوم سفید و رنگ کلاه نفر دوم سیاه باشد. در این حالت ابتدا از نفر اول می‌خواهند تا رنگ کلاهش را بگوید. نفر اول در جلوی خودش یک کلاه سفید و یک کلاه سیاه می‌بیند و می‌داند در کل دو کلاه سفید و دو کلاه سیاه وجود دارد. پس از رنگ کلاه خود مطمئن نیست و با افتخار این موضوع را اعلام می‌کند. پس از آن از نفر دوم می‌خواهند تا رنگ کلاهش را بگوید. نفر دوم در جلوی خود یک کلاه سفید می‌بیند. از طرفی می‌داند که نفر اول نتوانسته رنگ کلاه خود را بگوید پس به این نتیجه می‌رسد که رنگ کلاهش سفید نیست چون اگر سفید می‌بود نفر قبلی با دیدن دو کلاه سفید به این نتیجه می‌رسید که رنگ کلاهش سیاه است. پس نفر دوم می‌گوید که رنگ کلاهش سیاه است و پیتزا را دریافت می‌کند.

• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

باشگاه هکر‌‌های جوان، مدرسه‌ای برای تربیت هکر‌ها است. در مراسم فارغ‌التحصیلی باشگاه، که به کلاه‌گذاری معروف است، هکر‌ها در یک صف می‌ایستند و بر روی سر هر کدام از آن‌ها یک کلاه می‌گذارند که آینده‌ی آن‌ها را مشخص خواهد کرد. کلا‌ه‌ها سفید یا سیاه هستند. کلاه‌سفید‌ها هدف کمک به جامعه و کلاه‌سیاه‌ها هدف دیگری(؟) دارند.

تعداد فارغ‌التحصیلان امسال $n$ نفر است و در انبار $w$ کلاه سفید و $b$ کلاه سیاه وجود دارد. همه‌ی دانش‌آموختگان نیز از موجودی انبار باخبر هستند. در صف، هر فرد تنها از رنگ کلاه افراد جلویی‌اش با‌خبر است و حتی رنگ کلاه خودش را نمی‌داند. یعنی فردی که در ابتدای صف ایستاده، رنگ کلاه هیچ‌کس را نمی‌داند و فردی که در انتهای صف است، رنگ کلاه همه به جز خودش را می‌داند.

در انتهای مراسم کلاه‌گذاری، افراد یک به یک و از انتهای صف از مراسم خارج می‌شوند. هر فرد قبل از خارج شدنش اگر از رنگ کلاهش مطمئن باشد، رنگ کلاهش را اعلام می‌کند و به عنوان جایزه پیتزا می‌گیرد (گفتنی است که هکر‌ها، علاقه‌ی شدید به پیتزا دارند!). البته به خاطر کمبود بودجه باشگاه، فقط به اولین فردی که رنگ کلاهش را درست تشخیص بدهد، پیتزا می‌دهند. اگر فردی نیز از رنگ کلاهش مطمئن نباشد، بلند و با افتخار اعلام می‌کند که رنگ کلاهش را نمی‌داند تا افراد باقی‌مانده در مراسم (افرادی که در صف جلوی او قرار داشتند) را نیز از نگون‌بختی‌اش مطلع کند.

امیر نفر $i$ ام صف از انتها است. برای نمونه اگر امیر در انتهای صف باشد، $i=1$ است. در چند حالت از کلاه‌گذاری هکر‌ها، امیر صاحب پیتزا می‌شود؟ دو کلاه‌گذاری متفاوت هستند اگر هکری وجود داشته باشد که در یکی از آن‌ها، کلاه‌سفید و در دیگری کلاه‌سیاه باشد. با توجه به این‌که این مقدار می‌تواند بزرگ باشد، باقی‌مانده آن را بر $10^9 + 7$ حساب کنید.

به توضیحات ورودی و خروجی‌های نمونه توجه کنید!

ورودی🔗

در سطر اول ورودی به ترتیب چهار عدد صحیح و نامنفی $b$، تعداد کلاه‌های سیاه، $w$، تعداد کلاه‌های سفید، $n$، تعداد فارغ‌التحصیلان و $i$، مکان امیر نسبت به انتهای صف آمده است. $0\leq b, w, n\leq 2000$ $1\leq i\leq n\leq b + w$

خروجی🔗

در تنها سطر خروجی، پاسخ مسئله را چاپ کنید.

زیرمسئله‌ها🔗

الف) $b,w,n \leq 20$ (۳۰ نمره)

ب) بدون محدودیت اضافی (۷۰ نمره)

ورودی نمونه ۱🔗

1 1 2 1

خروجی نمونه ۱🔗

2

در این نمونه یک کلاه سفید و یک کلاه سیاه موجود است پس رنگ کلاه نفر اول و دوم متفاوت است. وقتی از نفر اول رنگ کلاهش را می‌پرسند با دیدن رنگ کلاه نفر بعد و دانستن اینکه از هر رنگ فقط یک کلاه وجود دارد می‌تواند رنگ کلاه خود را مشخص کند.

ورودی نمونه ۲🔗

1 1 2 2

خروجی نمونه ۲🔗

0

ورودی نمونه ۳🔗

2 1 2 1

خروجی نمونه ۳🔗

1

ورودی نمونه ۴🔗

2 2 3 2

خروجی نمونه ۴🔗

4

در این نمونه یکی از حالت‌های ممکن این است که رنگ کلاه نفر اول و سوم سفید و رنگ کلاه نفر دوم سیاه باشد. در این حالت ابتدا از نفر اول می‌خواهند تا رنگ کلاهش را بگوید. نفر اول در جلوی خودش یک کلاه سفید و یک کلاه سیاه می‌بیند و می‌داند در کل دو کلاه سفید و دو کلاه سیاه وجود دارد. پس از رنگ کلاه خود مطمئن نیست و با افتخار این موضوع را اعلام می‌کند. پس از آن از نفر دوم می‌خواهند تا رنگ کلاهش را بگوید. نفر دوم در جلوی خود یک کلاه سفید می‌بیند. از طرفی می‌داند که نفر اول نتوانسته رنگ کلاه خود را بگوید پس به این نتیجه می‌رسد که رنگ کلاهش سفید نیست چون اگر سفید می‌بود نفر قبلی با دیدن دو کلاه سفید به این نتیجه می‌رسید که رنگ کلاهش سیاه است. پس نفر دوم می‌گوید که رنگ کلاهش سیاه است و پیتزا را دریافت می‌کند.