• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

فامیل دور که در کار در فعالیت دارد، به شعار‌های خود پایبند است. برای همین یک نمایش نامه طراحی کرده است که در آن غیر از کلمات شعار‌های او از کلمات دیگری استفاده نمی‌شود! در این نمایش نامه $n$ نقش با شماره‌های ۱ تا $n$ وجود دارد که نقش $i$ ام را شخصی به نام $s_i$ اجرا می‌کند. امکان دارد که یک نفر دو یا چند نقش را نیز بازی کند اما امکان ندارد که یک نفر دو نقش پشت سر هم را بازی کند؛ یعنی نمی‌شود یک نفر هم نقش $i$ را بازی کند و هم نقش $i+1$ را.

حالا نمایش نامه به این صورت اجرا می‌شود:

ابتدا نفری که نقش اول را بازی می‌کند به نفری که نقش دوم را بازی می‌کند می‌گوید:«که با این در اگر در بند در مانند، درمانند.» سپس نفر دوم به نفر اول می‌گوید:«درمانند؟» و نفر اول با خونسردی جواب می‌دهد:«درمانند.». سپس نفری که نقش دوم را بازی می‌کند، به نفری که نقش سوم را بازی می‌کند می‌گوید:«که با این در اگر در بند در مانند، درمانند.». سپس نفر سوم به دوم می‌گوید:«درمانند؟» و نفر دوم به نفر اول می‌گوید:«درمانند؟» و او دوباره با خونسردی جواب می‌دهد:«درمانند.» و نفر دوم به نفر سوم با خونسردی می‌گوید:«درمانند.». سپس نفر سوم به نفری که نقش چهارم را بازی می‌کند می‌گوید:«که با این در اگر در بند در مانند، درمانند.» و او می‌پرسد:«درمانند؟» و نفر سوم از دوم می‌پرسد:«درمانند؟» و نفر دوم از اول می‌پرسد:«در‌مانند؟» و او با خونسردی جواب می‌دهد:«درمانند.» و...

برای مثال اگر ما ۴ نقش داشته باشیم که به ترتیب نقش‌ها را مهدی، علی، کامران و علی بازی کنند، دیالوگ‌ها به صورت زیر می‌شوند:

مهدی به علی: که با این در اگر در بند در مانند، در مانند.

علی به مهدی: در مانند؟

مهدی به علی: در مانند.

علی به کامران: که با این در اگر در بند در مانند، در مانند.

کامران به علی: در مانند؟

علی به مهدی: در مانند؟

مهدی به علی: در مانند.

علی به کامران: در مانند.

کامران به علی: که با این در اگر در بند در مانند، در مانند.

علی به کامران: در مانند؟

کامران به علی: در مانند؟

علی به مهدی: در مانند؟

مهدی به علی: در مانند.

علی به کامران: در مانند.

کامران به علی: در مانند.

حالا فامیل دور می‌خواهد دیالوگ‌های نمایش‌نامه را بنویسد اما وقتی شما را دارد کی بهتر از شما؟

ورودی🔗

در سطر اول ورودی عدد $n$ آمده است که نمایانگر تعداد نقش‌ها می‌باشد. سپس در $n$ خط بعدی، در هر خط، یک اسم می‌آید که نمایانگر اسم شخصی است که نقش $i$‌ را بازی می‌کند. تمامی اسامی رشته‌هایی متشکل از حروف کوچک و بزرگ انگلیسی بوده و طول هر کدام حداکثر ۲۰ می‌باشد. $1 \le n \le 100$

خروجی🔗

خروجی شامل تعدادی سطر است که نمایانگر دیالوگ این نمایش‌نامه می‌باشد.

مثال🔗

ورودی نمونه ۱🔗

2
T
U

خروجی نمونه ۱🔗

T to U: ke ba in dar agar dar bande dar manand, dar manand.
U to T: dar manand?
T to U: dar manand.

ورودی نمونه ۲🔗

3
parsa
divar
parsa

خروجی نمونه ۲🔗

parsa to divar: ke ba in dar agar dar bande dar manand, dar manand.
divar to parsa: dar manand?
parsa to divar: dar manand.
divar to parsa: ke ba in dar agar dar bande dar manand, dar manand.
parsa to divar: dar manand?
divar to parsa: dar manand?
parsa to divar: dar manand.
divar to parsa: dar manand.

ورودی نمونه ۳🔗

4
mahdi
ali
kamran
mahdi

خروجی نمونه ۳🔗

mahdi to ali: ke ba in dar agar dar bande dar manand, dar manand.
ali to mahdi: dar manand?
mahdi to ali: dar manand.
ali to kamran: ke ba in dar agar dar bande dar manand, dar manand.
kamran to ali: dar manand?
ali to mahdi: dar manand?
mahdi to ali: dar manand.
ali to kamran: dar manand.
kamran to mahdi: ke ba in dar agar dar bande dar manand, dar manand.
mahdi to kamran: dar manand?
kamran to ali: dar manand?
ali to mahdi: dar manand?
mahdi to ali: dar manand.
ali to kamran: dar manand.
kamran to mahdi: dar manand.

• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

فامیل دور که در کار در فعالیت دارد، از دیبی خواهش کرده است که یک شب به جای آی مجری برای بچه‌ها کتاب قصه بخواند. دیبی هم برای اینکه یک کتاب قصه بردارد، مجبور شد که یک کتاب قصه برندارد و به صورت رندم از بین کتاب‌های غیر قصه کتاب CLRS را انتخاب کرد. او شب کتاب را از آخر باز کرد تا برای بچه‌ها آن را از اول خوانده باشد! شاید برایتان عجیب باشد که آخر کتاب CLRS مبحث مرج سرت باشد اما در قصه‌ی این سوال که اینگونه است؛ پس دیبی شروع به خواندن مبحث مرج سرت کرد. خواندن مرج‌سرت دیبی اینقدر محیرالعقول بود که باعث شد که فامیل دور ایده‌ای برای بهتر کردن زمان مرج‌سرت به ذهنش برسد!! جیگر هم که معتقد است روش فامیل دور غلط است، به او یک آرایه $n$ تایی از اعداد داد که مرتب کند. روش فامیل دور برای مرتب کردن آرایه به این صورت است:

او ابتدا قسمت‌های صعودی پشت سر هم آرایه را پیدا می‌کند و طول هر کدام را روی کاغذ می‌نویسد. برای مثال اگر آرایه $1, 3, 5, 4, 6$ باشد، قسمت‌های صعودی پشت سر هم آرایه دو تا است: $1, 3, 5$ و $4, 6$ که طول اولی ۳ و دومی ۲ می‌باشد. پس فامیل دور دو عدد ۳ و ۲ را روی کاغذ می‌نویسد. او $k$ عدد روی کاغذ می‌نویسد. سپس اینگونه شروع به مرتب کردن آرایه می‌کند که هر دفعه دو قسمت صعودی مجاور از آرایه را انتخاب می‌کند و آن‌ها را شبیه مرج سرت مرج می‌کند؛ یعنی اینکه بعد از این کار این دو قسمت صعودی تبدیل به یک قسمت صعودی می‌شوند. به عبارت دیگر او این دو قسمت را به یک قسمت مرتب شده تبدیل می‌کند. سپس دو عدد مربوط به این دو قسمت را از روی کاغذ پاک می‌کند و اندازه‌ی قسمت جدید را جای این دو عدد روی کاغذ می‌نویسد. همچنین او برای مرج کردن دو قسمت پشت سر هم به اندازه‌ی مجموع اندازه‌شان (یعنی مجموع اعدادی که روی کاغذ برای این دو قسمت نوشته بود) باید زمان صرف کند. حالا فامیل دور برای اینکه کَلِ جیگر را بخواباند می‌خواهد در سریعترین زمان ممکن آرایه را مرتب کرده و به جیگر تحویل دهد. چون او از قصه‌ی دیبی به شدت خوابش گرفته است، شما به او بگویید که این کمترین زمان چقدر است.

ورودی🔗

در سطر اول ورودی دو عدد $n$ و $k$‌ آمده است.

سپس در سطر بعدی $k$ عدد می‌آید که $i$ امین عدد نمایانگر $i$ امین عددی است که فامیل دور روی کاغذ نوشته است. $1 \le n \le 10^9$ $1 \le k \le 100$ تضمین می‌شود که جمع اعداد آمده در سطر دوم ورودی برابر $n$ می‌باشد و همچنین همه‌شان اعدادی طبیعی بین ۱ تا $n$ می‌باشند.

خروجی🔗

در تنها سطر خروجی کمترین زمان برای مرتب کردن آرایه را خروجی دهید.

مثال🔗

ورودی نمونه ۱🔗

10 3
1 3 6

خروجی نمونه ۱🔗

14

توضیح نمونه‌ی ۱: روش بهینه این است که ابتدا دو قسمت اول را با هم یکی کنیم و سپس دو قسمت به وجود آمده را با هم یک قسمت کنیم. هزینه‌ی مرج اول ۴ و هزینه‌ی مرج دوم ۱۰ می‌باشد که در مجموع ۱۴ می‌شود.

ورودی نمونه ۲🔗

7 4
1 1 1 4

خروجی نمونه ۲🔗

12

ورودی نمونه ۳🔗

2 2
1 1

خروجی نمونه ۳🔗

2

ورودی نمونه ۴🔗

4 3
1 2 1

خروجی نمونه ۴🔗

7

• محدودیت زمان: ۲ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

فامیل دور که در کار در فعالیت دارد، به تازگی مسئول در آزمایشگاه شده است. او می‌خواهد از کار‌های داخل آزمایشگاه سر در بیاورد. فامیل دور که خیلی به کارش حساس است، هرچیزی که از در رد می‌شود را یادداشت می‌کند. به همین دلیل او یک لیست از تمامی مواد داخل آزمایشگاه دارد. همچنین او با مشاهدات طولانی تمامی واکنش‌ها را هم به خاطر سپرده است. هر واکنش به شکل $a_1 + a_2 + a_3 ... + a_p \rightarrow b_1 + b_2 + b_3 + ... + b_q$ است. یعنی اگر در واکنشی همه‌ی $a_1$ تا $a_p$ وجود داشته باشد، همه‌ی $b_1$ تا $b_q$ به وجود می‌آیند. همه‌ی $a$ها متفاوت و همه‌ی $b$ها متفاوت اند ولی ممکن است $i$ و $j$ی وجود داشته باشد که $a_i = b_j$(مانند کاتالیزگرها). حالا فامیل می‌خواهد بداند با این واکنش‌ها چه موادی را می‌تواند داشته باشد. دقت کنید هر ماده‌ای را می‌توان به هر اندازه‌ای رقیق کرد(یعنی اگر از یک نوع ماده در یک زمان داشته باشیم، می‌توانیم برای همیشه از آن استفاده کنیم).

ورودی🔗

در سطر اول ورودی سه عدد طبیعی $n$ و $m$ و $k$ آمده‌است که به ترتیب نشان‌دهنده‌ی تعداد مواد شناخته شده، تعداد مواد موجود در آزمایشگاه و تعداد واکنش‌ها است.

در سطر بعد $m$ عدد آمده است که نشان‌دهنده‌ی مواد موجود در آزمایشگاه هستند. تضمین میشود این اعداد طبیعی، متفاوت و نابیشتر از $n$ هستند.

سپس $k$ واکنش می‌آید. هر واکنش دارای سه سطر ورودی است. سطر اول حاوی دو عدد طبیعی مانند $p$ و $q$ است.

در سطر دوم $p$ عدد متفاوت آمده‌است که نشان‌دهنده‌ی واکنش‌دهنده‌ها هستند.

و در سطر سوم $q$ عدد متفاوت آمده که نمایان‌گر فراورده‌های واکنش هستند.

$1 \le n, m, k \le 300\ 000$

مجموع همه‌ی $p$ و $q$ها حداکثر سیصدهزار است.

خروجی🔗

در سطر اول خروجی عدد $t$ را چاپ کنید که نمایانگر تعداد موادی است که می‌توان در آزمایشگاه داشت.(مواد اولیه هم باید حساب شوند)

در سطر بعدی $t$ عدد را چاپ کنید که نشان‌دهنده‌ی موادی‌ است که می‌توان آن‌ها را در آزمایشگاه داشت. اعداد باید متفاوت و صعودی باشند.

مثال🔗

ورودی نمونه ۱🔗

5 2 3
5 4
2 1
2 3
1
2 1
3 4
2
2 1
4 5
3

خروجی نمونه ۱🔗

5
1 2 3 4 5

ورودی نمونه ۲🔗

5 2 3
1 2
2 2
1 2
1 4
3 1
1 2 4
5
2 1
3 4
5

خروجی نمونه ۲🔗

4
1 2 4 5

ورودی نمونه ۳🔗

9 1 5
1
2 2
1 2
3 4
1 1
1
2
3 2
1 3 4
5 6
4 3
1 2 5 6
2 3 7
2 1
7 8
9

خروجی نمونه ۳🔗

7
1 2 3 4 5 6 7

• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

فامیل دور که در کار در فعالیت دارد، در یک جدول مربع شکل درگیر پیدا کردن بچه فامیل شده است. فامیل در خانه تقاطع سطر اول و ستون اول جدول قرار دارد، غافل از اینکه بچه فامیل به خانه تقاطع سطر آخر و ستون آخر جدول رفته است. بچه فامیل در مسیر خود تعدادی رد پا هم به جا گذاشته است. به طوری که در هر سطر و هر ستون دقیقا روی یک خانه ردپا دیده می‌شود. فامیل به دنبال بچه فامیل، در هر حرکت می‌تواند به یکی از چهار خانه مجاور ضلعی خانه فعلی اش برود. همچنین اگر در هشت خانه مجاور راسی اش ردپایی ببیند به امید پیدا کردن بچه فامیل می‌تواند در یک حرکت به آن خانه هم برود. فامیل که از پیدا کردن بچه فامیل ناامید شده با وجود شما افق های روشنی پیش روی خودش می‌بیند. برای اینکه فامیل را ناامید نکنید کمترین تعداد حرکتی که می‌تواند فامیل را به بچه فامیل برساند، به او اعلام کنید.

ورودی🔗

در سطر اول ورودی عدد $n$ می‌آید که برابر با تعداد سطر‌ها و ستون‌های جدول است.

در سطر بعدی $n$ عدد متفاوت بین ۱ تا $n$ می‌آید که $i$مین آن‌ها $p_i$ است و به معنای وجود ردپا در خانه تقاطع سطر $p_i$ و ستون $i$ است. $1 \le n \le 300\ 000$

$1 \le p_i \le n$

خروجی🔗

در تنها سطر خروجی کمترین تعداد حرکتی که می‌تواند فامیل را به بچه فامیل برساند باید چاپ شود.

مثال🔗

ورودی نمونه ۱🔗

5
4 3 2 5 1

خروجی نمونه ۱🔗

6

ورودی نمونه ۲🔗

4
4 2 1 3

خروجی نمونه ۲🔗

4

• محدودیت زمان: ۲ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

فامیل دور که در کار در فعالیت دارد، با دیدن سردر دانشگاه تهران تصمیم به شروع به تحصیلات در این دانشگاه گرفت. او به دانشکده‌ی هنرهای زیبای دانشگاه تهران رفت و تحصیل در رشته‌ی درها را شروع کرد. (متاسفانه حرف‌های نادرستی بین مردم در رابطه با این دانشکده وجود دارد؛ از جمله عدم وجود رشته‌ی درها در این دانشکده.)

موعد امتحان میان‌ترم درس "در کشی صنعتی" هفته‌ی آینده است و فامیل دور باید برای این امتحان تمرین کند. برای همین یک کاغذ A4 که داخل آن بصورت یک جدول شطرنجی با $n$ سطر و $m$ ستون مشخص شده‌است، تهیه کرد تا تعدادی در برای تمرین روی آن بکشد. سطرهای این جدول را از بالا به پایین و ستون‌های جدول را از چپ به راست شماره‌گذاری کرد و خانه‌ی شطرنجی در سطر شماره $i$ و ستون شماره‌ $j$ را با $(i, j)$ مشخص کرد. او در کشیدن نمای روبروی "در گاراژ" مشکل دارد و همه‌ی وقت برای تمرینش را به کشیدن چنین درهایی اختصاص داده است. شماتیک یک در گاراژ با مختصات $(a, b, c, d, e, f)$ در نقشه به شکل زیر است:

دقت کنید که باید شرایط $b < e < f < c$ و $a < d$ صادق باشند.

فامیل، $q$ درِ گاراژ در مختصات‌های مختلف صفحه‌ی شطرنجی‌اش رسم کرد. او حین رسم‌کردن این شکل‌ها بسیار محو ترسیم بود، بطوری که حتی فراموش کرد درهای قبلی را پاک کند! در نتیجه تعدادی از این درها روی هم افتادند. حال پس از اتمام تمرین، او با یک صفحه شامل $q$ "در گاراژ" درهم و برهم مواجه شد. فامیل دور پس از کمی تماشای این صحنه، به فکر این افتاد که حساب کند در مجموع، چند خانه از $n \times m$ خانه‌‌ی جدول شطرنجی در این صفحه رنگی هستند؟ (و این کار شماست!)

ورودی🔗

در سطر اول ورودی سه عدد $n$ و $m$ و $q$ آمده‌اند که به ترتیب نمایانگر تعداد سطرهای جدول شطرنجی، تعداد ستون‌های جدول شطرنجی و تعداد درهای گاراژ کشیده‌شده است.

سپس در هریک از $q$ سطر بعدی، مختصات یک در گاراژ کشیده‌شده توسط فامیل دور به شکل ۶ عدد آمده‌است که به ترتیب نمایانگر اعداد $a$ و $b$ و $c$ و $d$ و $e$ و $f$ هستند که در توصیف شماتیک یک در گاراژ از نمای روبرو (عکس داخل صورت سوال) آمده‌اند.

$1 \le n, m \le 4000$ $1 \le q \le 200\ 000$ $b < e < f < c$$a < d$

تضمین می‌شود که کل نماهای توصیف شده درون جدول شطرنجی قرار می‌گیرند.

خروجی🔗

در تنها سطر خروجی یک عدد چاپ کنید که برابر تعداد خانه‌های رنگی در جدول شطرنجی فامیل است.

مثال🔗

ورودی نمونه ۱🔗

14 17 1
8 3 15 12 5 13

خروجی نمونه ۱🔗

85

این مثال، شکل صورت سوال است.

ورودی نمونه ۲🔗

14 23 2
8 3 15 12 5 13
10 14 21 12 15 20

خروجی نمونه ۲🔗

108

شکل این مثال:

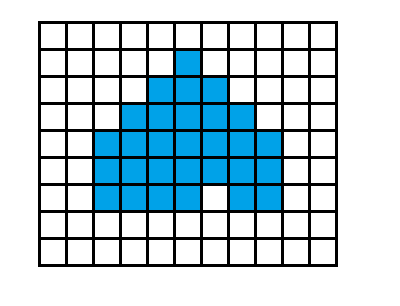
ورودی نمونه ۳🔗

9 11 1
5 3 9 7 6 8

خروجی نمونه ۳🔗

29

شکل این مثال:

• محدودیت زمان: ۶ ثانیه
• محدودیت حافظه: ۶۰۰ مگابایت

فامیل دور که در کار در فعالیت دارد، می‌خواهد به فامیل دورش سر بزند. اما متاسفانه فامیل دورش، خیلی دور است طوری که هنوز راه‌های بین خانه‌ی این دو نفر هنوز حتی ساخته هم نشده اند. روستایی که این دو فامیل در آن زندگی می‌کنند مانند یک جدول $n \times m$ است که فامیل دور در خانه‌ی (۱,۱) یعنی گوشه‌ی پایین و چپ جدول و خانه‌ی فامیل دور فامیل دور در خانه‌ی $(n,m)$ یعنی خانه‌ی راست و بالای جدول قرار دارد. در یک حرکت فامیل دور می‌تواند از خانه‌ای که هست یک خانه به بالا یا راست برود. در ابتدا تمام خانه‌ی های جدول(حتی خانه‌ی (۱,۱) و $(n,m)$ ) غیر قابل استفاده اند و فامیل دور نمی‌تواند از آن‌ها برای رفتن به خانه‌ی فامیلش استفاده کند.

به زودی انتخابات کدخدای روستا برگزار می‌شود. برای همین کدخدا (برای اینکه دور بعد انتخاب شود) تصمیم گرفته است که سریعا روستا را آسفالت کند. او در هر لحظه یک زیر مستطیل از روستا را انتخاب کرده و آسفالت می‌کند. هنگامی‌ که یک خانه آسفالت شود، فامیل دور می‌تواند از آن خانه برای رسیدن به خانه‌ی فامیلش استفاده کند. او به شما گزارش لحظه به لحظه‌ی آسفالت شدن خانه‌ها را می‌دهد و شما باید به ازای هر لحظه به او بگویید که با توجه به گزارش‌های تا پایان این لحظه آیا یک مسیر از خانه‌اش به خانه‌ی فامیلش وجود دارد که تمامی خانه‌های این مسیر آسفالت باشد یا خیر.

ورودی🔗

در سطر اول ورودی سه عدد $n$ و $m$‌ و $q$ آمده است که به ترتیب نمایانگر ابعاد جدول و تعداد لحظات آسفالت شدن خانه‌ها می‌باشد. سپس در $q$ سطر بعدی، در سطر $i$م، خانه‌هایی که در لحظه‌ی $i$ آسفالت شده اند به صورت زیر آمده است:

چهار عدد $x_1$، $y_1$، $x_2$ و $y_2$ آمده اند که به ترتیب دو عدد اول نمایانگر مختصات نقطه‌ی پایین و چپ و دو عدد دوم نمایانگر مختصات خانه‌ی بالا و راست از مستطیلی می‌باشند که در این لحظه تمامی خانه‌های آن آسفالت شده است. $1 \le n,m \le 10^{18}$ $1 \le q \le 1000$ $1 \le x_1 \le x_2 \le n$ $1 \le y_1 \le y_2 \le m$ دقت کنید که امکان دارد یک خانه دو یا چند بار آسفالت شود که این موضوع اصلا عجیب نیست!! (اگر هست به خیابان‌های دور و برتان نگاهی بیاندازید)

خروجی🔗

خروجی شامل $q$ سطر است که در سطر $i$م باید بگویید که آیا در لحظه‌ی $i$، با توجه به گزارش‌های تا پایان این لحظه، یک مسیر از خانه‌ی فامیل دور به خانه‌ی فامیل دور فامیل دور وجود دارد که تمامی خانه‌هایش آسفالت باشند یا خیر. اگر این مسیر وجود داشت عبارت "yes" و اگر وجود نداشت عبارت "no" را چاپ کنید.

مثال🔗

ورودی نمونه ۱🔗

5 5 3
1 1 3 3
1 1 4 4
1 1 5 5

خروجی نمونه ۱🔗

no
no
yes

ورودی نمونه ۲🔗

2 2 3
1 2 1 2
2 1 2 1
2 2 2 2

خروجی نمونه ۲🔗

no
no
no

ورودی نمونه ۳🔗

2 2 4
1 2 1 2
2 1 2 1
2 2 2 2
1 1 1 1

خروجی نمونه ۳🔗

no
no
no
yes

• محدودیت زمان: ۳ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

فامیل دور که در کار در فعالیت دارد، در انتها به شهرش دور بازگشته تا همانطور که از بچگی آرزو داشته به شهرش خدمت کند. دور، شهر بی دفاع، از تعدادی محله تشکیل شده که تعدادی خیابان بینشان وجود دارد. از ویژگی های ممتاز دور که اهالی دور به آن افتخار می‌کنند این است که اگر حداقل ۴ محله مختلف را دور یک دایره قرار دهیم به طوری که بین هر دو محله که دور دایره کنار هم قرار گرفته اند خیابانی وجود داشته باشد، حداقل یک خیابان وجود دارد که دو تا از این محله ها که دور دایره کنار هم قرار نگرفته اند را به هم وصل کند.

در اولین قدم مسئولیت ساماندهی مرکز شهر به فامیل محول شده است. مرکز شهر را تعدادی محله تشکیل می‌دهند که بین هر دوتایشان خیابان وجود داشته باشد و تعداد این محله ها بیشینه مقدار ممکن باشد. فامیل می‌خواهد تعداد محله های مرکز شهر را بفهمد تا پیش‌بینی های لازم را انجام دهد. او از شما کمک می‌خواهد تا بتواند از اولین ماموریت در خدمت به شهرش سربلند بیرون بیاید.

مثال🔗

ورودی🔗

در سطر اول ورودی دو عدد $n$ و $m$ می‌آید که نشان دهنده تعداد محله‌ها‌ و تعداد خیابان‌های شهر دور است. در ادامه $m$ سطر می‌آید که در $i$مین آن‌ها دو عدد $a_i$ و $b_i$ می‌آید که نشان دهنده وجود خیابان بین محله های $a_i$ و $b_i$ است. تضمین می‌شود که بین هر دو محله حداکثر یک خیابان وجود دارد. $1 \le n, m \le 1\ 000\ 000$ $1 \le m \le \frac {n (n - 1)} 2$ $1 \le a_i, b_i \le n$ $a_i \neq b_i$

خروجی🔗

در تنها سطر خروجی تعداد محله های مرکز شهر باید چاپ شود.

ورودی نمونه ۱🔗

5 8
1 2
2 3
3 4
4 5
5 1
1 3
1 4
3 5

خروجی نمونه ۱🔗

4

ورودی نمونه ۲🔗

6 7
1 2
2 3
2 4
2 5
5 1
5 4
5 6

خروجی نمونه ۲🔗

3