• محدودیت زمان: ۰.۵ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

دیجیکالا برای ارسال بسته‌های سنگین مانند یخچال و غیره نیاز به دقیقاً دو نفر دارد که بتوانند بسته را جابه‌جا کنند. از این رو دو نفر را به عنوان پیک استخدام کرده است. هر کدام از این دو نفر در بازه‌هایی از روز‌های ماه می‌توانند سر کار بروند. حالا مسئولین دیجیکالا می‌خواهند بدانند که در چند روز از ماه آنها می‌توانند بسته‌های سنگین را ارسال کنند.

ورودی🔗

در سطر اول ورودی دو عدد $n$ و $m$‌ می‌آید که به ترتیب نمایانگر تعداد بازه‌هایی است که پیک اول و دوم سر کار می‌آیند. سپس در $n$ خط بعدی در هر خط یک بازه‌‌ی کاری پیک اول می‌آید. بعد از آن در هر یک از $m$ خط بعدی یکی از بازه‌های کاری پیک دوم می‌آید. همچنین نحوه ورودی دادن بازه‌ها به این شکل است:

در یک خط دو عدد $l$ و $r$ می‌آید که اولی نمایانگر شروع بازه و دومی نمایانگر پایان بازه می‌باشد.$1 \le n,m \le 10$ $1 \le l \le r \le 30$

دقت کنید که هیچ کدام از دو بازه‌ی یک پیک با هم اشتراک ندارند. همچنین تمام بازه‌ها شامل نقطه‌ی شروع و پایان نیز می‌شوند. همچنین توجه کنید که در ورودی هیچ یک از بازه‌های کاری یک پیک دو بار نخواهد آمد.

خروجی🔗

در تنها خط خروجی تعداد روزهایی را که دیجیکالا می‌تواند بسته‌ی سنگین ارسال کند را خروجی دهید.

مثال🔗

ورودی نمونه ۱🔗

3 2
1 8
9 15
18 25
15 20
8 10

خروجی نمونه ۱🔗

7

توضیح: روزهایی که دیجیکالا می‌تواند بسته‌ی سنگین ارسال کند:

8 ، 9 ، 10 ، 15 ، 18 ، 19 ، 20

• محدودیت زمان: ۰.۵ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

تعداد $n$ آکواریم خالی از آب به طول و عرض‌های برابر و ارتفاع‌های متفاوت را به هم چسبانده‌ایم و آن‌ها را از چپ به راست با اعداد ۱ تا $n$ به ترتیب شماره‌گذاری کرده‌ایم؛ به طوری که ارتفاع آکواریم شماره‌ی $i$، $h_i$ می‌باشد. (شکل پایین) سپس $q$ عملیات روی آکواریم‌ها به این صورت انجام می‌دهیم:

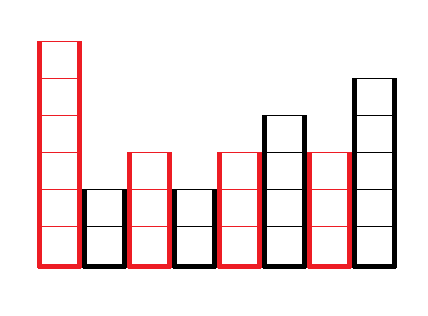
یکی از آکواریم‌ها را انتخاب کرده و اینقدر روی آن آب می‌ریزیم تا به اندازه‌ی یک واحد ارتفاعش زیاد شود. امکان دارد که در این بین از آکواریمی که ما انتخاب کرده‌ایم آب به آکواریم‌های بغلی و از آنها به دیگران سرریز کند اما دقت کنید که آب فقط از یک آکواریم به سمت آکواریم سمت راست و یا سمت چپ آن سرریز می‌کند و به بیرون از مجموعه آکواریم‌‌ها سر ریز نمی‌کند.

برای درک بهتر به مثال زیر دقت کنید:

فرض کنید که الان وضعیت آکواریم‌ها به صورت زیر باشد.

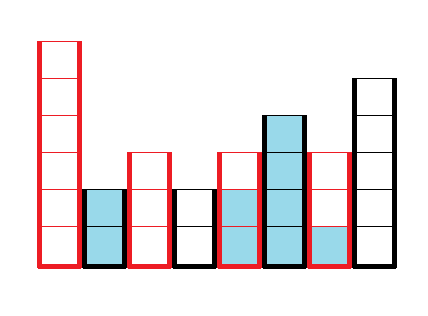
حالا اگر ما بخواهیم یک عملیات روی ششمین آکواریم از سمت چپ انجام بدهیم این اتفاق می‌افتد:

زمانی که روی آکواریم شماره‌ی ۶ آب می‌ریزیم، آب از آن داخل آکواریم شماره‌ی ۵ و ۷ سرریز می‌کند و در نتیجه آکواریم شماره‌ی ۵ و ۷ پر می‌شود و سرریز می‌کند داخل بقیه و همینطور که تا آخر پیش برویم، برای اینکه در نهایت ارتفاع آکواریم شماره‌ی ۶ یک واحد زیاد شود، نیازمندیم که اینقدر آب بریزیم تا وضعیت آکواریم‌ها به این صورت شود.

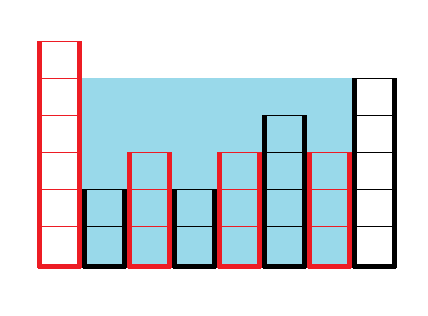
حالا وظیفه‌ی شما در این سوال این است که اولین جایی را که در این بین آبی به آکواریم شماره‌ی ۱ یا $n$ سرریز می‌کند، خروجی دهید. یعنی باید شماره‌ی اولین عملیاتی را خروجی دهید که در حین انجام آن آب به آکواریم شماره‌ی ۱ یا $n$ سرریز کند.

ورودی🔗

در سطر اول ورودی دو عدد $n$ و $q$ می‌آید که به ترتیب نمایانگر تعداد آکواریم‌ها و تعداد عملیات‌ها می‌باشد.

سپس در خط بعدی $n$ عدد می‌آید که با یک فاصله از هم جدا شده‌اند و عدد $i$ ام نمایانگر $h_i$ می‌باشد.

بعد از آن $q$ خط می‌آید که در خط $i$، $d_i$ می‌آید که نمایانگر آکواریم انتخابی برای عملیات $i$ است. دقت کنید که آکواریم انتخابی هیچ‌گاه آکواریم شماره‌ی ۱ و یا $n$ نخواهد بود. ورودی عملیات‌ها به ترتیب انجام آنها خواهد بود یعنی اولین ورودی مربوط به اولین عملیات می‌باشد و دومین ورودی مربوط به دومین عملیات می‌باشد و همینطور تا آخر. $3 \le n, q \le 100$ $1 \le h_i \le 20$ $2 \le d_i \le n-1$

خروجی🔗

در تنها سطر خروجی شماره‌ی اولین عملیاتی را که در حین انجام آن آب به آکواریم شماره‌ی ۱ یا $n$‌ می‌رسد خروجی دهید. اگر در حین انجام هیچکدام از این عملیات‌ها آب به آکواریم‌ شماره‌ی ۱ یا $n$‌ سرریز نکرد، عبارت "No Answer" را خروجی دهید.

مثال🔗

ورودی نمونه ۱🔗

5 8
5 2 1 3 4
2
2
4
4
4
4
3
2

خروجی نمونه ۱🔗

7

ورودی نمونه ۲🔗

4 3
3 4 2 3
3
3
2

خروجی نمونه ۲🔗

No Answer

ورودی نمونه ۳🔗

4 4
1 4 2 3
3
3
2
3

خروجی نمونه ۳🔗

No Answer

ورودی نمونه ۴🔗

4 8
3 4 2 1
3
3
2
2
2
2
2
2

خروجی نمونه ۴🔗

7

• محدودیت زمان: ۰.۵ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

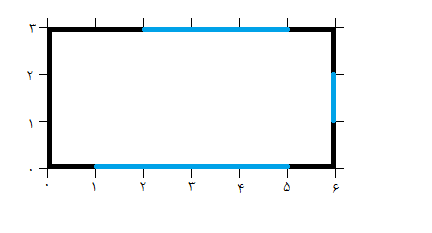
سوپرمن در یک اتاق گیر کرده است که اتاق پر است از آینه‌های قدی که ارتفاعشان به اندازه‌ی دیوار است؛ یعنی از بالا تا پایین دیوار را می‌پوشانند اما از نظر عرض، با دیوار یکسان نبوده و عرض متفاوتی دارند. همچنین اتاق چهار دیوار کناری دارد که اگر از بالا به آن نگاه کنیم، دیوار بالایی و دیوار پایینی $n$ متر و دیوار سمت چپ و سمت راست $m$ متر می‌باشند. حال روی دیوار بالایی و پایینی حرکت کرده و از چپ به راست به ازای هر یک متر یک علامت روی آن‌ها می‌گذاریم. همچنین روی دیوار‌های سمت چپ و سمت راست حرکت کرده و از پایین به بالا به ازای هر متر یک علامت می‌گذاریم. سپس علامت ‌های روی دیوار پایینی و بالایی را از چپ به راست با $0$ تا $n$ و دیوار‌ سمت چپ و سمت راست را از پایین به بالا با $0$ تا $m$ به صورت زیر شماره‌گذاری می‌کنیم. یعنی اینکه اگر مثلا $n=6$ و $m=3$ اتاق (اگر از بالا به آن نگاه کنیم) به همراه علامت‌ها و شماره‌گذاری‌ها به این صورت خواهد بود:

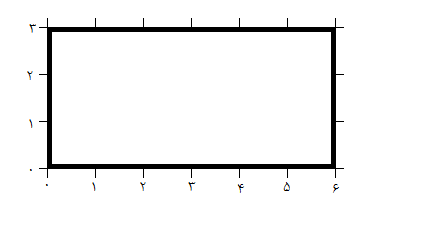
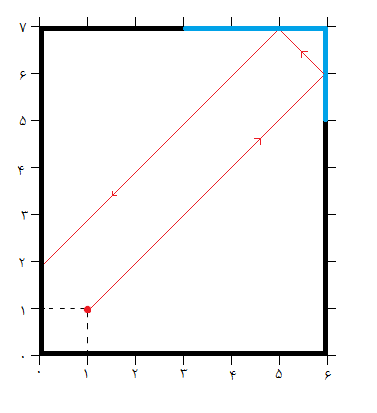
در این اتاق $k$ آینه وجود دارد که آینه‌ی شماره‌ی $i$، روی یکی از دیوارها قرار دارد و با توجه به شماره‌گذاری‌های روی دیوارها از شماره‌ی $l_i$ شروع می‌شود و تا $r_i$ ادامه می‌یابد. برای مثال اگر روی‌ همان مثال بالا یک آینه‌ روی دیوار سمت راست با $l=1$ و $r=2$ و همینطور یک آینه روی دیوار بالایی با $l=2$ و $r=5$ و یک آینه روی دیوار پایین با $l=1$ و $r=5$ قرار دهیم، شکل اتاق (اگر از بالا به آن نگاه کنیم) به این صورت خواهد شد:

طبق فیلم‌نامه سوپرمن باید با استفاده از لیزر گازی که گریمر فیلم در درون چشمش جاگذاری کرده است، دیوار را سوراخ کرده و از اتاق بیرون بیاید اما مشکلی که وجود دارد این است که سوپرمن باید لیزرش را به جهتی بفرستد که به دیوار برخورد کند چرا که امکان دارد لیزر به آینه‌ها خورده و همینطور تا بی‌نهایت بازتاب کند و هیچ‌گاه به دیوار برخورد ننماید. از این رو سوپرمن باید لیزر خود را در جهت درستی بتاباند. کارگردان فیلم به نظرش آمده است که اگر سوپرمن در مکان $(x,y)$ بایستد (یعنی جوری بایستد که فاصله‌‌اش از دیوار پایینی $y$ متر و از دیوار سمت چپ $x$ متر باشد) و لیزرش را در جهت $(mx, my, 0)$ (یعنی بدون مولفه‌ی $z$، درنتیجه ارتفاع فوتون‌های لیزر از زمین هیچگاه تغییر نخواهد کرد. البته این‌ها با فرض ذره‌ای بودن نور است که فرضی علمی نیست! ) بتاباند، از نظر فیلم برداری بسیار عالی خواهد بود اما مشکلی که وجود دارد این است که کارگردان نمی‌داند که آیا در این صورت لیزر به دیوار برخورد خواهد کرد یا نه و اگر برخورد می‌کند، بگویید که در چه مختصاتی برخورد می‌کند تا مقدمات انفجار در آن نقطه فراهم شود.

از آنجایی که سوپرمن یک فیلم است و به‌کار مسائل واقعی زندگی نمی‌آید، تهیه‌کننده‌ی فیلم تصمیم گرفت که در ازای ۱۲۵ امتیاز از شما جواب سوالش را بخواهد.

دیگر تصمیم خودتان است و شما مختارید‍!!

به نکات و محدودیت‌های گفته شده در بخش ورودی توجه کنید!

ورودی🔗

در سطر اول ورودی سه عدد صحیح $n$، $m$ و $k$‌ آمده است که به ترتیب نمایانگر طول دیوار بالا و پایین به متر، طول دیوار سمت چپ و راست به متر و تعداد آینه‌ها می‌باشند.

در سطر دوم ورودی چهار عدد صحیح $x$، $y$، $mx$ و $my$ می‌آید که دو عدد اول نمایانگر مکانی است که کارگردان می‌خواهد سوپرمن در آن‌جا بایستد و دو عدد دوم نمایانگر برداری است که کارگردان می‌خواهد سوپرمن لیزر را در آن جهت بتاباند.

سپس $k$‌ سطر در ورودی می‌آید که در $i$امین سطر آن، توضیح مربوط به آینه‌ی $i$ام به این صورت سه عدد $d_i$ و $l_i$ و $r_i$ می‌آید:

عددطبیعی $d_i$ نمایانگر این است که این آینه روی کدام دیوار قرار دارد:

• اگر این عدد برابر با 1 باشد به این معنی است که آینه روی دیوار بالایی قرار دارد.
• اگر این عدد برابر با 2 باشد به این معنی است که آینه روی دیوار پایینی قرار دارد.
• اگر این عدد برابر با 3 باشد به این معنی است که آینه روی دیوار سمت چپ قرار دارد.
• اگر این عدد برابر با 4 باشد به این معنی است که آینه روی دیوار سمت راست قرار دارد.

در آینه‌های روی دیواره‌های چپ و راست تضمین می‌شود که $0 \le l_i \le r_i \le m$.

در آینه‌های روی دیواره‌های بالا و پایین تضمین می‌شود که$0 \le l_i \le r_i \le n$

نکته: پرتو‌ نور در گوشه‌های هر آینه نیز بازتاب می‌شود. اگر پرتو لیزر به گوشه‌ی مستطیل اتاق رسید، می‌توانید فرض کنید که نور بازتاب نمی‌شود (حتی اگر آن نقطه گوشه‌ی آینه‌ای باشد) و همان‌جا با دیوار برخورد می‌کند.

همچنین تضمین می‌شود که آینه‌ها با هم تلاقی ندارند.$4 \le n, m\le 200$$0 \le k\le 200$ $1 \le x \le n-1$ $1 \le y \le m-1$ $0 \le mx,my \le 200$

تضمین می‌شود همیشه نقطه‌ی برخورد لیزر با آینه‌ها در دیوار مختصاتی صحیح خواهد بود.

خروجی🔗

در تنها سطر خروجی اگر لیزر به دیوار برخورد نمی‌کرد و تا بی‌نهایت بین آینه‌ها بازتاب می‌کرد عبارت "No" را خروجی دهید و اگر لیزر به دیوار برخورد می‌کرد مختصات نقطه‌ای از دیوار را خروجی دهید که لیزر به آن برخورد می‌کند. (مختصات را با فرض اینکه گوشه‌ی تلاقی دیوار چپ و پایین اتاق مرکز مختصات دکارتی است خروجی دهید.)

ورودی نمونه ۱🔗

6 7 2
1 1 7 7
4 5 7
1 3 6

خروجی نمونه ۱🔗

0 2

توضیح: در نمونه‌ی اول لیزر در نقطه‌ی (۶,۶) به آینه‌ی شماره‌ی ۱ برخورد می‌کند. سپس بعد از بازتاب در نقطه‌ی (۵,۷) به آینه‌ی دوم برخورد می‌کند و بعد از بازتاب در نقطه‌ی (۰,۲) به دیوار برخورد می‌نماید.

ورودی نمونه ۲🔗

6 7 4
1 1 7 7
1 0 6
2 0 6
3 0 7
4 0 7

خروجی نمونه ۲🔗

6 0

ورودی نمونه ۳🔗

4 4 2
3 2 1 0
4 1 3
3 1 3

خروجی نمونه ۳🔗

No

• محدودیت زمان: ۰.۵ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

برنامه‌ای بنویسید که با ورودی گرفتن $n$، $n$ امین شکل الگوی زیر را خروجی دهد. (به مثال‌ها دقت کنید)

خروجی شما در این سوال باید دقیقا برابر مثال داده شده باشد؛ فاصله (space) کم یا اضافه بعنوان اشتباه درنظر گرفته می‌شود.

ورودی🔗

در تنها سطر خروجی عدد $n$ آمده است.

خروجی🔗

در خروجی $n$ امین شکل الگوی زیر را خروجی دهید. $1 \le n \le 100$

مثال🔗

ورودی نمونه ۱🔗

1

خروجی نمونه ۱🔗

    *
   * *
  *   *
 *     *
*********

ورودی نمونه ۲🔗

2

خروجی نمونه ۲🔗

        *
       * *
      *   *
     *     *
    *********
   * *     * *
  *   *   *   *
 *     * *     *
*****************

ورودی نمونه ۳🔗

3

خروجی نمونه ۳🔗

            *
           * *
          *   *
         *     *
        *********
       * *     * *
      *   *   *   *
     *     * *     *
    *****************
   * *     * *     * *
  *   *   *   *   *   *
 *     * *     * *     *
*************************

• محدودیت زمان: ۳ ثانیه
• محدودیت حافظه: ۵۱۲ مگابایت

هم اکنون دیجیکالا می‌خواهد برای سرویس دهی به $n$ شهر، تعدادی دفتر در نقاط مختلف تاسیس کند. پس از این تاسیس‌ها، باید تعدادی سیستم ارسال بسته بین شهرها و دفترها تعریف شود. هر سیستم ارسال بسته می‌تواند از یک شهر یا دفتر شروع شده و در یک شهر یا دفتر به اتمام برسد. می‌توان شهرها را بصورت نقاطی داخل صفحه مختصات دکارتی در نظر گرفت که شهر $i$ در مختصات $(x_i, y_i)$ قرار دارد. تاسیس هر دفتر هزینه‌ی $D$ دارد و تعریف هر سیستم ارسال بسته به اندازه‌ی فاصله‌ی ابتدا و انتهای سیستم، هزینه خواهد داشت. هدف این است که با داشتن محل شهرها و مقدار $D$، روشی بهینه برای تاسیس دفترها و تعریف سیستم‌های ارسال بسته ارائه شود که:

1. بتوان به هر شهر از یک دفتر بسته ارسال کرد؛ یعنی هر شهر بوسیله‌ی سیستم‌های ارسال بسته بصورت مستقیم یا غیر مستقیم به حداقل یک دفتر مسیر داشته باشد. بصورت مستقیم یعنی یک سیستم ارسال بسته از این شهر به یک دفتر وجود داشته باشد و غیر مستقیم یعنی بتوان با دنباله‌ای از سیستم‌های ارسال بسته، بسته را از این شهر پس از گذراندن از تعدادی شهر دیگر به یک دفتر رساند.
2. میزان هزینه‌ی کلی کمینه شود.

برای مثال همیشه می‌توان با تاسیس $n$ دفتر که هریک در یکی از شهر‌ها قرار دارد، با هزینه‌ی برابر $n \times D$ به هدف گفته‌شده رسید. همچنین می‌توان با یافتن مرکز ثقل همه‌ی شهرها و تاسیس یک دفتر در آنجا، با هزینه‌ی برابر $D$ + (مجموع فاصله‌ی شهرها از مرکز ثقل) به هدف گفته‌شده رسید؛ اما معمولا هیچیک از این دو راه‌حل گفته‌شده کم‌خرج ترین راه‌حل نیستند!

در این سوال تعدادی تست وجود دارد که مختصات شهرها در آن برگرفته از مختصات تعدادی شهر در دنیای‌ واقعی است. برنامه‌ی شما هرچه با هزینه‌ی کمتری بتواند به هدف گفته شده برسد، امتیاز بیشتری کسب خواهد نمود.

در هر تستی که به برنامه‌ی شما داده می‌شود، مقدار پیش بینی شده برای هزینه یا $expected$ همراه نقشه به شما داده می‌شود و اگر شما بتوانید با هزینه‌ی کمتر یا مساوی $expected$ به هدف گفته شده برسید، نمره‌ی آن تست را دریافت می‌کنید. توجه کنید که راهکار شما لازم نیست بهترین راهکار باشد؛ کافیست از مقدار پیش بینی‌شده بهتر باشد تا خروجی شما درست در نظر گرفته شود.

۱۰ نقشه در تست‌ها وجود دارد که هریک ۳ بار آمده است که مقدار‌ $expected$ در آن‌ها متفاوت است. تعداد ارسال‌های شما در این سوال تاثیری روی رتبه‌ی شما ندارد.

ورودی🔗

در سطر اول ورودی سه عدد طبیعی $n$ و $D$ و $expected$ آمده‌است.

عدد $n$ نمایانگر تعداد شهر‌های داخل نقشه است، عدد $D$ نمایانگر هزینه‌ی تاسیس هر دفتر است و عدد $expected$ برابر هزینه‌ی پیش بینی شده برای پروژه است.

سپس در $n$ سطر بعدی مختصات $n$ شهر در نقشه آمده‌است. مختصات شهر $i$ بصورت $x_i\ y_i$ آمده‌است که: $-1000 \le x_i, y_i \le 1000$

$1 \le n \le 100$

خروجی🔗

در سطر اول خروجی دو عدد $k$ و $m$ چاپ کنید که به ترتیب نمایانگر تعداد دفاتری که می‌خواهید تاسیس کنید و تعداد سیستم‌های ارسال بسته هستند.

سپس در هریک از $k$ سطر بعدی مختصات یک دفتر را بصورت $x\ y$ خروجی دهید.

سپس در هریک از $m$ سطر بعدی دو مختصات خروجی دهید که نمایانگر دو سر یک سیستم ارسال بسته در نقشه‌ی مالی ارائه شده‌ی شما هستند.

امکان تاسیس یک دفتر روی مختصات شهرها وجود دارد؛ در این حالت نیازی به خروجی دادن سیستم ارسال بسته بین دفتر و شهر هم مختصات نیست.

مثال🔗

ورودی نمونه ۱🔗

4 10 40
1 0
0 1
-1 0
0 -1

خروجی نمونه ۱🔗

4 0
1 0
0 1
-1 0
0 -1

هزینه‌ی ساخت نقشه‌ی خروجی این نمونه برابر ۴۰ است.

ورودی نمونه ۲🔗

4 10 15
1 0
0 1
-1 0
0 -1

خروجی نمونه ۲🔗

1 4
0 0
0 0 1 0
0 0 0 1
0 0 -1 0
0 0 0 -1

هزینه‌ی ساخت نقشه‌ی خروجی این نمونه برابر ۱۴ است.