+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
There is an ancient saying that problem I is always one of the hardest problems in programming contests.
Colonel believes the above ancient saying, but what are the probabilities that you’re writing the last problem of the problem set, and there is only one problem slot left, and you contact the contest coordinator to see if they can place your problem on slot I, and they respond with “I is the only remaining slot”?
Lightning strike. Lightning strike indeed.
BUT THIS IS LAST YEAR’S STORY. This time Colonel put the dibs on writing problem I from day 1.
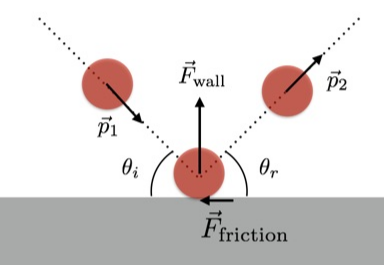
Colonel and Erfan were walking in TFB2DW (The Frictionless Bisected 2 Dimensional World), talking about this year’s hardest problem, each of them holding a 2d tennis ball. They suddenly thought whether or not the balls will collide at some point if they were to throw them. What makes the question a little harder though, is that there is an infinite wall in the TFB2DW (hence the name). If any of the 2d balls happen to touch the infinite wall, they will behave in the normal way that 2d balls behave when touching infinite walls. (Really. What else did you expect?)
And you know what? We’re asking you to give them the answer. What a surprise.
And here’s the “science” if you’re into that kind of stuff. There is no friction in our case, so $\theta_i$ will be equal to $\theta_r$.
# ورودی
There are multiple test cases in the input. The first line contains $T$, the number of test cases. $T$ test cases will then follow, Each of them contains real numbers defining the starting point of each of the balls, it’s moving direction, radius, and velocity(units/second), and two points which uniquely define the infinite wall. Here is the placeholder for one of the test cases in the input:
+ ball1StartX ball1StartY
+ ball1DirectionX ball1DirectionY
+ ball1Velocity ball1Radius
+ ball2StartX ball2StartY
+ ball2DirectionX ball2DirectionY
+ ball2Velocity ball2Radius
+ wallPoint1X wallPoint1Y
+ wallPoint2X wallPoint2Y
All of the numbers in the input are below $100$. Also it is guaranteed that balls won’t collide anytime after the $10^{12}$ th second, won’t share any point with the infinite wall or each other in the initial position, and won’t be immobile.
# خروجی
For each test case, if the two balls collide at some point, output a line containing `Lightning strike`, otherwise output `Not even a spark`.
# مثالها
## ورودی نمونه ۱
```
2
-20 4
1 -1
1 1
10 4
-1 -1
10 1
0 0
10 0
-20 4
1 -1
10 1
10 4
-1 -1
10 1
0 0
10 0
```
## خروجی نمونه ۱
```
Not even a spark
Lightning strike
```
In the first case, the second ball having a speed equal to ten times of that of the first ball will leave the scene in a blink of an eye. In the same setup but with equal velocities (second test case), the two balls will collide after hitting the wall.