+ محدودیت زمان: ۱ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- Minions have been on this planet far longer than we have. They're all different. But they all share the same goal. To serve the most despicable master they could find. After thousands of rough years, finally they found the most despicable master in the world, “Erfan.aa”. They are very happy so they’re having a celebration. After dancing, singing and all of those “heavy rejections”, the time for lunch has come. The great Minion “Sir Kevin” is very creative. He and $8$ other minions form a $3\times3$ grid waiting for Erfan to bring them bananas. The grid is shown in the following picture. Each circle indicates a cell.  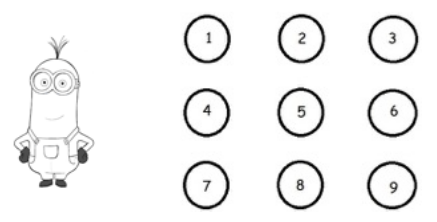Erfan has $N$ bananas. He will start from a cell on the grid and give a banana to the Minion on that cell and go to another cell, give another banana to the Minion on the new cell and so on... until he runs out of bananas. His movement among cells must obey the following rules: + The line connecting the current cell to the next cell should not pass through a cell with unfed Minion + Each Minion must be fed at most once. Example: If Erfan is on the cell $7$ and The minion on the cell $4$ is fed, he can move to the following cells: $1, 2, 5, 6, 8$ Erfan is very curious. He wants to know how many ways exist to do this task. He’s now busy in the celebration, Can you help him? # ورودی The first line of input shows the number of test cases $T$. $$1 \leq T \leq 100$$ Each of following $T$ lines contains two space separated integers $S$ and $N,$ indicating start cell and number of bananas respectively. $$ 1 \leq S, N \leq 9$$ # خروجی For each test case, print a single line `Case#<caseNumber> : <#PossibleWays>`. For more clarifications see Sample Output. # مثال‌ها ## ورودی نمونه ۱ ``` 4 1 2 5 2 2 1 3 3 ``` ## خروجی نمونه ۱ ``` Case#1 : 5 Case#2 : 8 Case#3 : 1 Case#4 : 31 ``` In the first test case: There are $5$ ways to do the task: $\{1 \to 2\},$ $\{1 \to 6\},$ $\{1 \to 5\},$ $\{1 \to 8\},$ $\{1 \to 4\}$.