+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
رئیس جمهور کشور کدکاپ میخواهد به هر استاندار تعدادی سکه جایزه بدهد. او میخواهد برای ایجاد رقابت بین استانها، به استاندارهایی که در دو استان همسایه قرار دارند تعداد سکه متفاوتی جایزه بدهد.

جادههای این کشور دو طرفهاند و بین دو استان کشیده شدهاند. میدانیم اگر از هر استان کشور کدکاپ شروع کنیم میتوانیم با رفتن به استانهای همسایه، به تمام استانهای کشور برسیم. همچنین تعداد جادهها بسیار کم است و به اندازه حداقل تعداد جاده برای رسیدن از تمام استانها به استانهای دیگر طراحی شده است. میتوان اثبات کرد که همیشه تعداد جادهها یکی کمتر از تعداد استانها است.
کمترین تعداد سکهای که رئیس جمهور برای جایزه دادن به استاندارها باید خرج کند به صورتی که استاندارهای هیچ دو استان مجاوری تعداد سکه برابر دریافت نکرده باشند، را محاسبه کنید.
# ورودی
در سطر اول ورودی، عدد صحیح و مثبت $t$ آمده که تعداد سناریوها را نشان میدهد. سپس در ادامه برای هر سناریو به ترتیب ورودیها داده میشوند.
$$1 \leq t \leq 300 \, 000$$
در سطر اول هر سناریو عدد صحیح و مثبت $n$ که نشانگر تعداد شهرها در سناریو $i$ام است ورودی داده میشود.
سپس در $n - 1$ خط بعدی جادههای کشور ورودی داده میشوند، در هر خط دو عدد صحیح و مثبت $v_i$ و $u_i$ داده میشود که دو استان مبدا و مقصد جاده را مشخص میکنند.
$$1 \leq n \leq 300 \, 000$$
$$1 \leq u_i, v_i \leq n$$
**تضمین میشود که مجموع $n$ روی همهی سناریوها حداکثر ۳۰۰،۰۰۰ باشد.**
# خروجی
خروجی $t$ سطر دارد که برای هر سناریو، در یک خط کمترین میزان سکه برای جایزه دادن به کل استانها را باید چاپ کنید.
# مثالها
## ورودی نمونه ۱
```
2
2
2 1
8
7 3
4 6
1 7
5 4
7 4
2 7
8 4
````
## خروجی نمونه ۱
```
3
11
````
<details class="green">
<summary>
**توضیح نمونه ۱**
</summary>
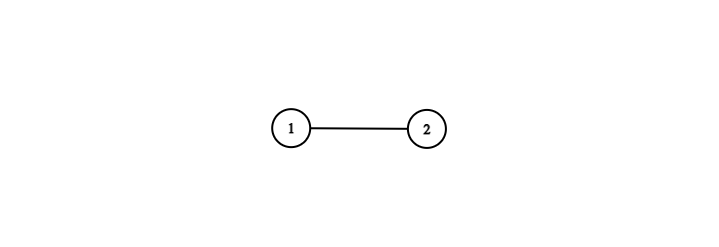
اگر به استان ۱، $1$ سکه و به استان ۲، $2$ سکه داده شود، هیچ دو استان مجاوری تعداد یکسانی سکه دریافت نمیکنند و این کمترین مجموع سکه ممکن را دارد. بنابراین پاسخ برابر $1 + 2 = 3$ است.
</details>
<details class="green">
<summary>
**توضیح نمونه ۲**
</summary>
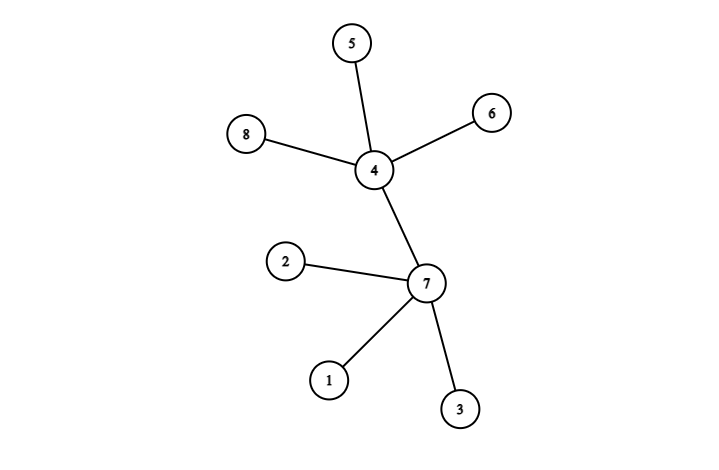
اگر به استان ۱، ۲، ۳، ۵، ۶ و ۸ $1$ سکه و به استان ۴، $2$ سکه و به استان ۷، $3$ سکه داده شود، هیچ دو استان مجاوری تعداد یکسانی سکه دریافت نمیکنند و این کمترین مجموع سکه ممکن را دارد. بنابراین پاسخ برابر $6 \times 1 + 2 + 3 = 11$ است.
</details>