+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
Hezardastan, a leading information technology group in Iran, has a huge data center containing $n$ servers and $m$ terminals (where $m \leq n$). A terminal is a pair of keyboard and monitor that can be connected to a server for administrative purposes. The servers are numbered $1$ through $n$ and the terminals are numbered $1$ through $m$. This data center has a network topology in which not every terminal is necessarily able to connect to every server. For example, the figure below depicts $3$ terminals and $6$ servers where a terminal can connect to a server if a line is drawn between them.
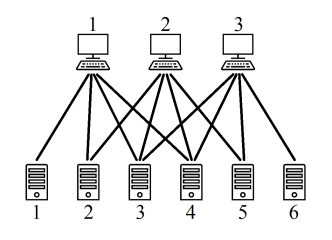
A subset $S$ of the servers with size $m$ is called *manageable* if its members are allowed by the network topology to be simultaneously managed by the terminals, i.e. each terminal can be connected to a distinct server in $S$. For example, the subset $\{2, 3, 6\}$ in the example above is manageable as its members can be respectively managed by the terminals $\{1, 2, 3\}$. A subset of the servers is called *unmanageable* if it has size $m$ and is not manageable. A network topology is called *totally manageable* when it causes no unmanageable subset of servers. For example, the network topology shown in the example above is totally manageable, but if the connection link between terminal $2$ and server $5$ is removed, then it will not be totally manageable anymore since the subsets $\{1, 5, 6\}$, $\{2, 5, 6\}$, $\{3, 5, 6\}$, and $\{4, 5, 6\}$ will become unmanageable. Given a network topology for the data center, you have to find if it is totally manageable or it makes an unmanageable subset.
# ورودی
The first line of input contains two integers $m$ and $n$ separated with a single space $(1 \leq m \leq 150, \, 1 \leq n \leq 400, \, m \leq n)$. The next $m$ lines describe the network topology by an $m \times n$ matrix. Each of these lines contains $n$ space-separated integers which are either $0$ or $1$. The $j$-th number (for $1 \leq j \leq n$) in the $(1 + i)$-th line of input (for $1 \leq i \leq m$) is $1$ if terminal $i$ can connect to server $j$, and it is $0$ otherwise.
# خروجی
If the given network topology is totally manageable, you only have to print $1$ in the first line of output. Otherwise, you should print $0$ in the first line of output and an unmanageable subset of servers in the second line in the form of $m$ space-separated integers (indicating the server numbers, in any arbitrary order). If there are multiple unmanageable subsets, you can print any one of them.
# مثالها
## ورودی نمونه ۱
```
3 6
1 1 1 1 0 0
0 1 1 1 1 0
0 0 1 1 1 1
````
## خروجی نمونه ۱
```
1
````
## ورودی نمونه ۲
```
3 6
1 1 1 1 0 0
0 1 1 1 0 0
0 0 1 1 1 1
````
## خروجی نمونه ۲
```
0
1 5 6
````
Network Topology in Hezardastan