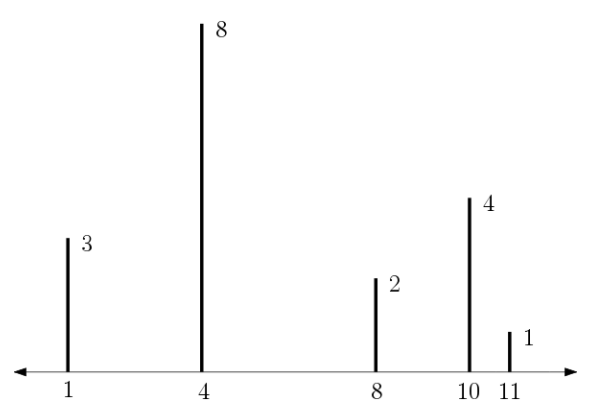
+ محدودیت زمان: ۲ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- There are $n$ wooden rods vertically placed over a horizontal line. The rods are numbered $1$ through $n$ from left to right. Each rod $i$ ($1 \leq i \leq n$) is placed at position $x_i$ and has a height $h_i$.  A termite wants to eat all the rods one by one. It starts eating from an arbitrary rod $s$ ($1 \leq s \leq n$). Then, after eating a rod $i$, the termite selects the next rod to eat based on the following method. Among the remaining rods $j$, the one with maximum $h_j - |x_i - x_j |$ is selected. If there are ties, the one with minimum $|x_i - x_j |$ is selected. If there are still ties, the left-most rod is selected. Your task is to calculate the total (horizontal) distance traveled by the termite to eat all the rods. # ورودی The first line of the input contains two space-separated integers $n$, the number of rods, and $s$, the starting rod number ($1 \leq s \leq n \leq 100\, 000$). The rods are described in the next $n$ lines. On the line $1 + i$ ($1 \leq i \leq n$), the $i$-th rod is specified with two space-separated integers $x_i$ ($|x_i | \leq 10^9$) and $h_i$ ($1 \leq h_i \leq 10^9$). Additionally, for each $i$ ($1 \leq i \leq n - 1$), $x_i \lt x_{i+1}$. # خروجی You should print a single integer denoting the total distance traveled by the termite. # مثال ## ورودی نمونه ۱ ``` 5 3 1 3 4 8 8 2 10 4 11 1 ``` ## خروجی نمونه ۱ ``` 17 ```