• محدودیت زمان: ۲ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

---

مارچلو در هنگام سپری کردن مسافرت رویایی خود بود که متوجه فقدانی در اوقات فراغت خود شد و آن چیزی نبود جز بازی بیلیارد! مارچلو که در این بازی تبحر خاصی داشت به سوی آلبرتو رفت تا توپ‌های بیلیارد را از او تحویل بگیرد. آلبرتو که به این راحتی‌ها به کسی توپ بیلیارد نمی‌داد، از او خواست که مسئله زیر را برایش حل کند!

آلبرتو در کل $\binom{n+1}{2}$ توپ بیلیارد دارد که در $n$ ردیف و در زیر هم چیده شده‌اند. به طور دقیق‌تر در ردیف $i$اُم، $i$ توپ بیلیارد طوری قرار گرفته‌اند که به جز توپ‌های ردیف پایین، هر توپ بر روی دو توپ دیگر قرار گرفته است.

اما از آنجایی که آلبرتو توپ‌های یک رنگ را دوست ندارد، برای همین تصمیم گرفته است که توپ‌های خود را رنگ کند. برای این کار، او توپ‌های ردیف پایین را با سیاه یا سفید رنگ می‌کند و سپس رنگ توپ‌های بالاتر را به صورت زیر بدست می‌آورد:

• اگر رنگ دو توپ موجود در زیر توپ مورد نظر برابر باشد، رنگ توپ بالایی سفید می‌شود.
• در غیر این صورت رنگ توپ مورد نظر سیاه خواهد شد.

برای مثال، شکل زیر مثالی برای $n = 4$ است که در ردیف پایین آن، سه توپ به رنگ سیاه درآمده‌اند:

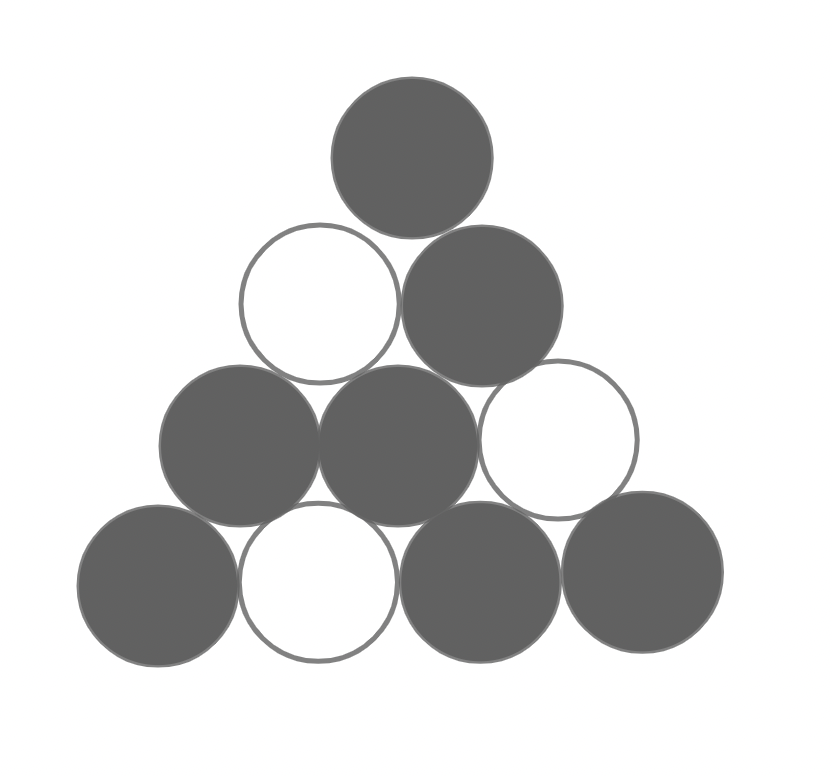
حال آلبرتو $p$ توپ از پایین‌ترین ردیف توپ‌های خود را به رنگ سیاه در می‌آورد. سپس در $k$ مرحله، در هر مرحله به احتمال برابری، دو توپ از $n$ توپ موجود در ردیف آخر را انتخاب می‌کند و جای آن‌ها را عوض می‌کند و پس از $k$ مرحله، رنگ توپ‌های دیگر را به دست می‌آورد. اکنون آلبرتو از مارچلو می‌خواهد تا احتمال این را محاسبه کند که پس از $k$ مرحله، توپ ردیف اول سیاه شود.

ورودی

ورودی شامل دو خط است که در خط اول به ترتیب اعداد $n$ و $k$ و $p$ با فاصله از هم آمده‌اند و در خط دوم $p$ عدد با فاصله از هم آمده است که عدد $i$اُم نشان‌دهنده‌ی $a_i$ است و به این معناست که توپ $a_i$اُم در ردیف آخر توپ‌های آلبرتو سیاه است. $$1 \le k \le 10^9$$ $$2 \le n \le 10^9$$ $$1 \le p \le 100$$ $$1 \le a_i \le n$$ تضمین می‌شود $a_i$ها متمایز و صعودی‌اند.

خروجی

در تنها خط خروجی احتمال خواسته شده را به پیمانه‌ی $10^9+7$ خروجی دهید. (می‌توان ثابت کرد احتمال این واقعه برابر با عبارت $\frac{P}{Q}$ است که در آن $P$ و $Q$ نسبت به هم اول هستند. شما باید مقدار $P \times Q^{-1}$ را به پیمانه‌ی $10^9 + 7$ خروجی دهید)

مثال

ورودی نمونه ۱

2 1 2
1 2

خروجی نمونه ۱

0

همواره دو توپ ردیف آخر سیاه‌اند پس توپ ردیف اول بعد از هر تعداد مرحله سفید است.

ورودی نمونه ۲

3 2 2
1 2

خروجی نمونه ۲

666666672

می‌توان محاسبه کرد که احتمال سیاه شدن توپ ردیف اول پس از دو مرحله $\frac{2}{3}$ است که به باقی مانده‌ی $10^9+7$ برابر با مقدار بالا می‌شود.