- محدودیت زمان: ۱ ثانیه
- محدودیت حافظه: ۶۴ مگابایت
امروز روز جهانیه ریاضیاته! و «آنالیز حقیقی» یکی از مباحث هیجان انگیز و دوست داشتنی اونه...
 %align_center_start%
%align_center_start%
دکتر مریم میرزاخانی
%align_end%
منظور از بازه $[a, b]$ (بخوانید بازه بسته $a$ و $b$) یعنی مجموعه تمام نقاط بین $a$ و $b$ (شامل $a$ و $b$) به عبارت دیگر یعنی:
$$[a, b] = { x \in \mathbb{R} | a \leq x \leq b }$$
منظور از بازه $(a, b)$ (بخوانید بازه باز $a$ و $b$) مجموعه تمام نقاط بین $a$ و $b$ (بدون $a$ و $b$) به عبارت دیگر یعنی:
$$(a, b) = { x \in \mathbb{R} | a < x < b }$$
محسن همه اعداد حقیقی بازه بسته $[1, 100]$ را یادداشت کرده است.
محسن $n$ بازه $[l_i, r_i]$ که ($1 \leq l_i \leq r_i \leq 100,$) در مجموعه اعداد خود را دوست دارد و اگر عددی از آن حذف شود، محسن ناراحت میشود. توجه کنید ممکن است این بازهها اشتراک داشتهباشند.
محسن در هر عملیات میتواند یک بازه باز مثل $(x, y)$ که ($1 \leq x < y \leq 100$) را انتخاب کند و همهی نقاط باقیمانده از مجموعه محسن را که در این بازه قرار دارد؛ از مجموعه محسن حذف کند.
محسن میخواهد با کمترین تعداد عملیات کاری کند که فقط بازههای مورد علاقه محسن در مجموعه او باقیبماند. (برای بهتر متوجه شدن سوال مثالها را مطالعه کنید.)
به محسن کمک کنید تا کمینه تعداد عملیات لازم را محاسبه کند. اگر انجام این کار با تعداد متناهی عملیات شدنی نیست این خبر بد را به محسن بگویید.
ورودی
در سطر اول ورودی عدد صحیح و مثبت $n$ آمده است که تعداد بازهها را نشان میدهد. $$1 \leq n \leq 100$$ در $n$ سطر بعدی در سطر$i$ دو عدد صحیح $l_i$ و $r_i$ آمده است. $$1 \leq l_i \leq r_i \leq 100$$
خروجی
در صورتی که با انجام عملیات فوق این کار شدنی است، کمینه تعداد عملیات لازم را چاپ کنید. در غیر این صورت -1 را چاپ کنید.
مثالها
ورودی نمونه ۱
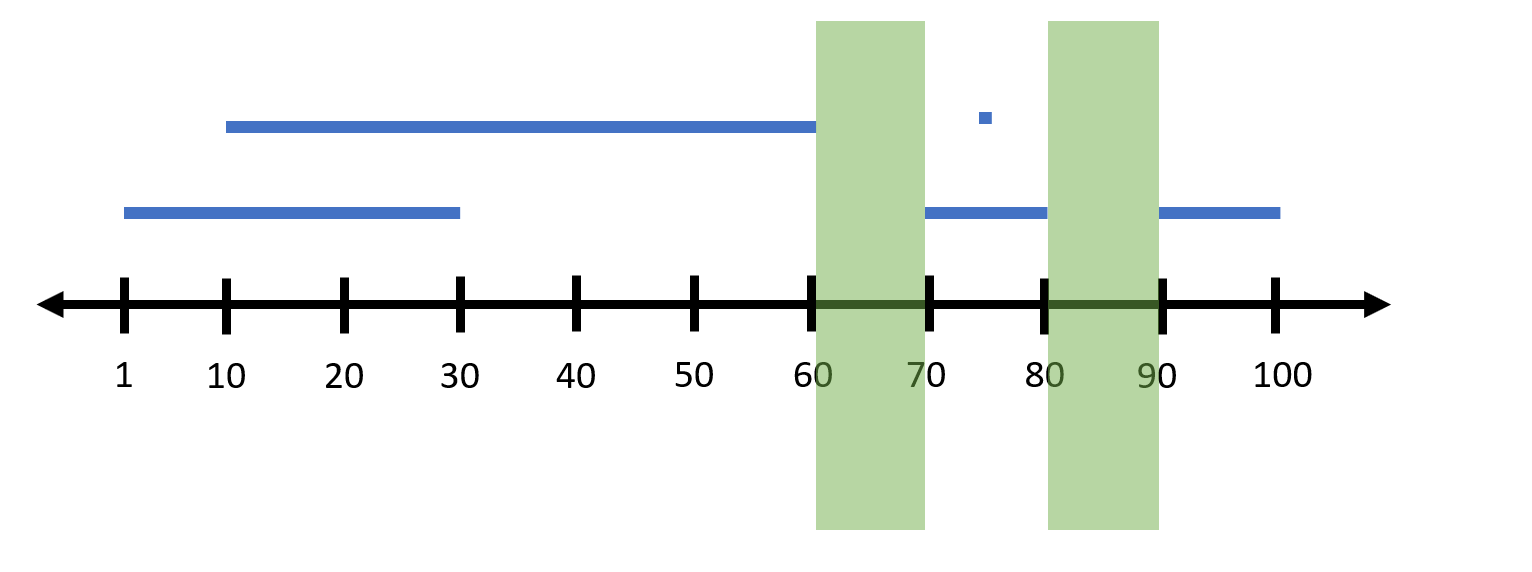
5
1 30
90 100
10 60
75 75
70 80
خروجی نمونه ۱
2
کافی است بازه $(60, 70)$ و بازه $(80, 90)$ حذف شود.
ورودی نمونه ۲
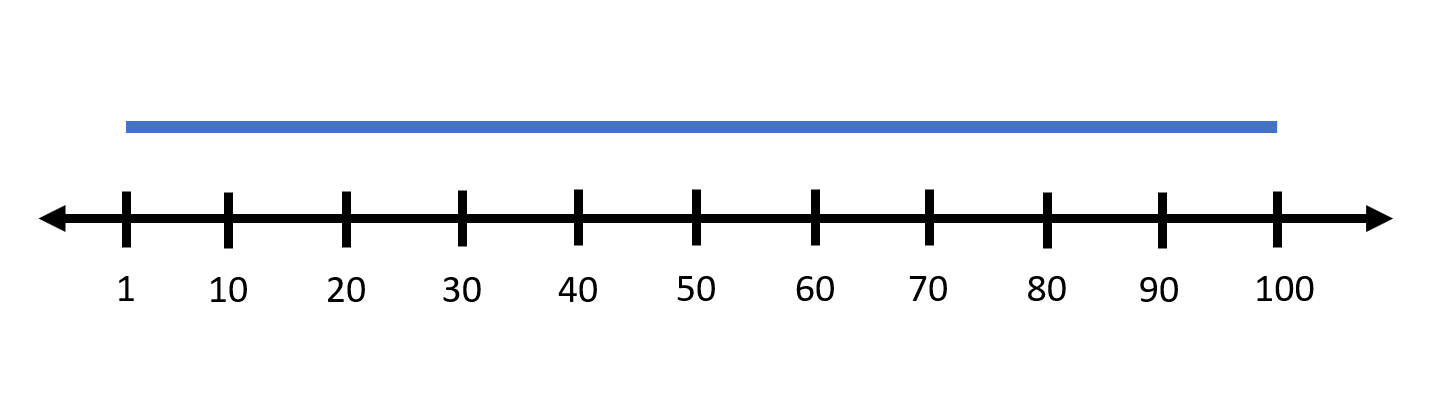
1
1 100
خروجی نمونه ۲
0
نیاز به حذف کردن هیچ بازهای نیست.
ورودی نمونه ۳
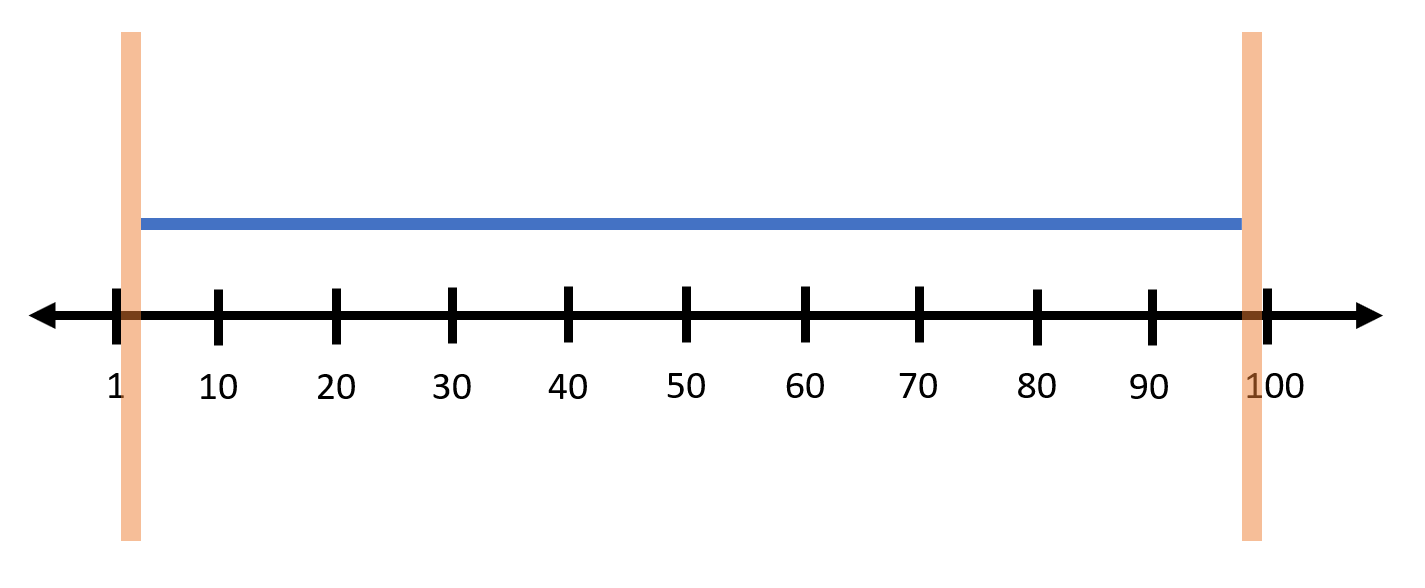
1
2 99
خروجی نمونه ۳
-1
بدون در نظر گرفتن بازههای مورد علاقه فقط بازه $[1, 2)$ و بازه $(99, 100]$ باقی میماند که نمی توان با تعداد متناهی بازه این دو بازه را پوشاند.
ارسال پاسخ برای این سؤال