• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۵۱۲ مگابایت
• منبع: JOI 2014

---

استاد مجتبی یک بازی جدید دانلود کرده است.

بازی شامل یک جدول \((m+2) \times n\) است که در آن توپی از یک خانه‌ای سطر اول به پایین پرت می‌شود و در نهایت به یک خانه از سطر \((m+2)\)ام می‌رسد.

در هریک از سطر‌های ۲ تا \((m+1)\)ام یک مانع سوراخ دار قرار دارد. مانع سوراخ دار سطر \(i\)ام را می‌توان با ۳ عدد \(A_{i}, B_{i}, C_{i}\) نشان داد (\(A_{i} \le C_{i} \le B_{i}\))، به این معنی که این مانع از خانه \((i,A_{i})\) تا خانه \((i,B_{i})\) را پوشش می‌دهد و در خانه \((i,C_{i})\) از آن یک سوراخ دارد. اگر توپ از بالا به این مانع برخورد کند، قل می‌خورد و از خانه ی دارای سوراخ خارج می‌شود و به مسیرش به سمت پایین ادامه می‌دهد.

برای قرار دادن مانع \(i\)ام، بازیکن باید \(D_{i}\) هزینه بپردازد. هدف بازی این است که بتوان با کمترین هزینه طوری مانع‌ها را قرار داد که توپ از هر یک از خانه‌های سطر اول شروع کند، به یک خانه یکسان از سطر آخر برسد (مثلا توپ از هرجا شروع کند به خانه‌ی دوم از سطر آخر برسد).

استاد که در بند سوراخ و خانه‌های خالی جدول نیست، از شما می‌خواهد که بازی را برای او انجام دهید.

ورودی

در سطر اول به ترتیب دو عدد \(m\) و \(n\) آمده اند. در سطر \(i\)ام از \(m\) سطر بعدی ورودی، ۴ عدد \(A_{i+1}\) ،\(B_{i+1}\) ،\(C_{i+1}\) و \(D_{i+1}\) آمده اند.

\[ 1 \le m \le 100\ 000 \] \[ 1 \le n \le 1\ 000\ 000\ 000\] \[ 1 \le A_{i+1}\le C_{i+1} \le B_{i+1} \le n\] \[ 1 \le D_{i+1} \le 1\ 000\ 000\ 000\]

خروجی

اگر کار خواسته شده در سوال امکان پذیر نیست عدد \(-1\)، و در غیر این صورت کمترین هزینه را چاپ کنید.

زیرمسئله‎ها

زیرمسئله	نمره	محدودیت
۱	۱۱	\( m \le 10, n \le 1\ 000 \)
۲	۱۸	\( m \le 200 \)
۳	۲۲	\( m \le 1\ 000 \)
۴	۴۹	بدون محدودیت اضافی

مثال

ورودی نمونه ۱

5 6
2 4 3 5
1 2 2 8
3 6 5 2
4 6 4 7
2 4 3 10

خروجی نمونه ۱

25

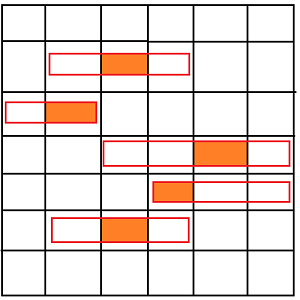
اگر از مانع‌های سطر سوم، پنجم و ششم استفاده کنیم، توپ با شروع از هر خانه سطر اول، به خانه سوم از سطر آخر می‌رسد.