- محدودیت زمان: ۱ ثانیه
- محدودیت حافظه: ۲۵۶ مگابایت
در شهر کدکاپآباد تنها یک خط مترو وجود دارد که هر روز تنها یک بار از ایستگاه ۱ شروع کرده و تا ایستگاه آخر میرود. $n$ ساکن این شهر هر روز صبح برای رفتن به سر کار از این خط مترو استفاده میکنند.
شهروند $i$ام اول صبح میخواهد از ایستگاه $s_i$ به ایستگاه $e_i$ برود. قطار شهر کدکاپآباد بسیار قدیمی است و حداکثر $L$ نفر میتوانند سوار آن شوند. هر فرد میتواند در ایستگاه $s_i$ سوار قطار شود و در یکی از ایستگاههای ادامهی مسیر پیاده شود و باقی مسیر را پیاده برود.
اگر شهروند $i$ام در ایستگاه $m_i$ از قطار پیاده شود باید $\mid m_i-e_i \mid$ واحد پیاده برود. زمان پیاده شدن هر شهروند از قطار طوری تعیین کنید که مجموع میزان پیاده روی شهروندان کمینه شود. (توجه کنید که $m_i$ میتواند برابر با $s_i$ باشد. یعنی شما میتوانید یکی از شهروندان را اصلاً سوار قطار نکنید.)
ورودی
در سطر اول ورودی، دو عدد صحیح و مثبت $n$ و $L$ آمده است که $n$ نشان دهندهی شهروندان شهر کدکاپآباد و $L$ نشان دهندهی حداکثر تعداد مسافر سوار بر قطار است.
$$1 \leq n, L \leq 100 , 000$$
در هر کدام از $n$ سطر بعدی، در سطر $i$ام $s_i$ و $e_i$ آمده است که نشان دهندهی مبدا و مقصد شهروند $i$ ام است. $$1 \leq s_i \lt e_i \leq 300 , 000$$
خروجی
کمینهی مجموع خستگی شهروندان را چاپ کنید.
مثالها
ورودی نمونه ۱
2 1
1 2
2 3
خروجی نمونه ۱
0
توضیح نمونه ۱
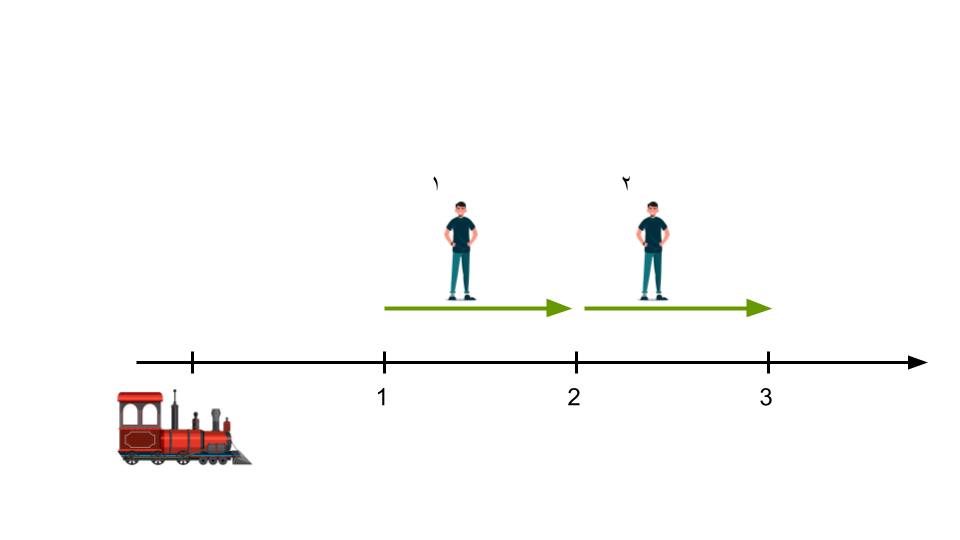
- در ایستگاه ۱ مسافر ۱ را سوار میکند.
- در ایستگاه ۲ مسافر ۱ را پیاده میکند و مسافر ۲ را سوار میکند.
- در ایستگاه ۳ مسافر ۲ را پیاده میکند.
به این ترتیب هر دو مسافرها در مقصدی که میخواهند پیاده میشوند. پس مجموع خستگیها $0 + 0 = 0$ میشود.
ورودی نمونه ۲
4 1
1 3
2 4
3 5
5 7
خروجی نمونه ۲
2
توضیح نمونه ۲
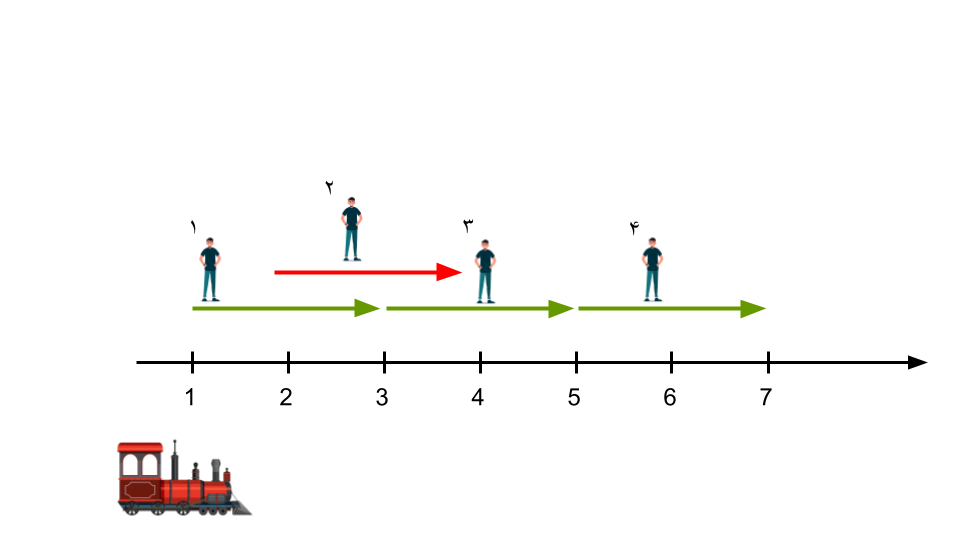
- در ایستگاه ۱ مسافر ۱ را سوار میکند.
- در ایستگاه ۳ مسافر ۱ را پیاده میکند و مسافر ۳ را سوار میکند.
- در ایستگاه ۵ مسافر ۳ را پیاده میکند و مسافر ۴ را سوار میکند.
- در ایستگاه ۷ مسافر ۴ را پیاده میکند.
به این ترتیب مسافرهای ۱، ۳ و ۴ در مقصدی که میخواهند پیاده میشوند ولی مسافر ۲ اصلاً سوار نشده و باید پیاده به مقصدش برود و بهاندازهی $\mid 4 - 2 \mid = 2$ خسته میشود. پس مجموع خستگیها $0 + 2 + 0 + 0 = 2$ میشود.
ورودی نمونه ۳
4 2
4 9
1 7
2 10
3 6
خروجی نمونه ۳
6
توضیح نمونه ۳
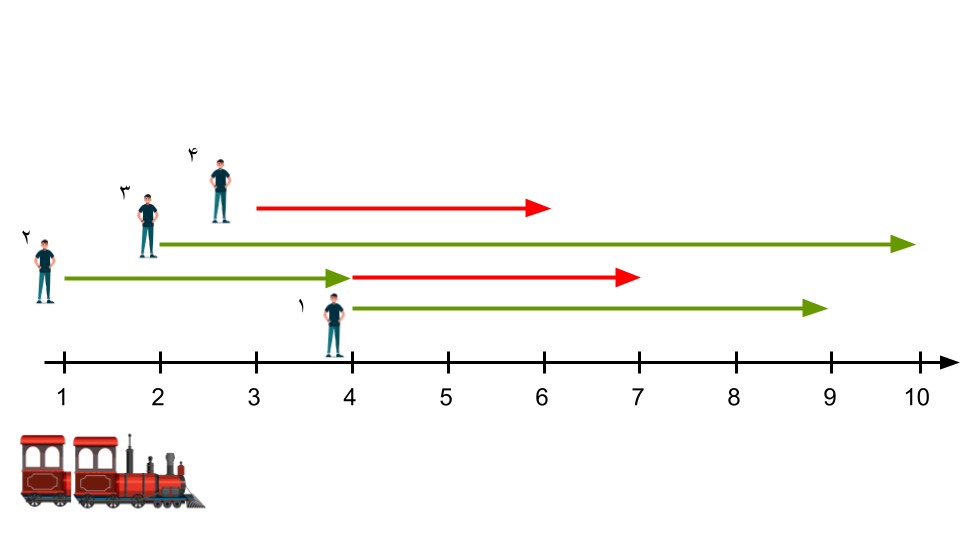
- در ایستگاه ۱ مسافر ۲ را سوار میکند.
- در ایستگاه ۲ مسافر ۳ را سوار میکند. (توجه کنید اینبار ۲ نفر ظرفیت دارد.)
- در ایستگاه ۴ مسافر ۲ را پیاده میکند و مسافر ۱ را سوار میکند.
- در ایستگاه ۹ مسافر ۱ را پیاده میکند.
- در ایستگاه ۱۰ مسافر ۳ را پیاده میکند.
به این ترتیب مسافرهای ۱ و ۳ در مقصدی که میخواهند پیاده میشوند ولی مسافر ۴ اصلاً سوار نشده و باید پیاده به مقصدش برود و بهاندازهی $\mid 6 - 3 \mid = 3$ خسته میشود. همچنین مسافر ۲ در ایستگاه ۴ پیاده شده ولی میخواست به ایستگاه ۷ برود و بهاندازهی $\mid 7 - 4 \mid = 3$ خسته میشود.
پس مجموع خستگیها $0 + 3 + 0 + 3 = 6$ میشود.
ارسال پاسخ برای این سؤال