• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

---

یک زنجیر مانند شکل زیر داریم:

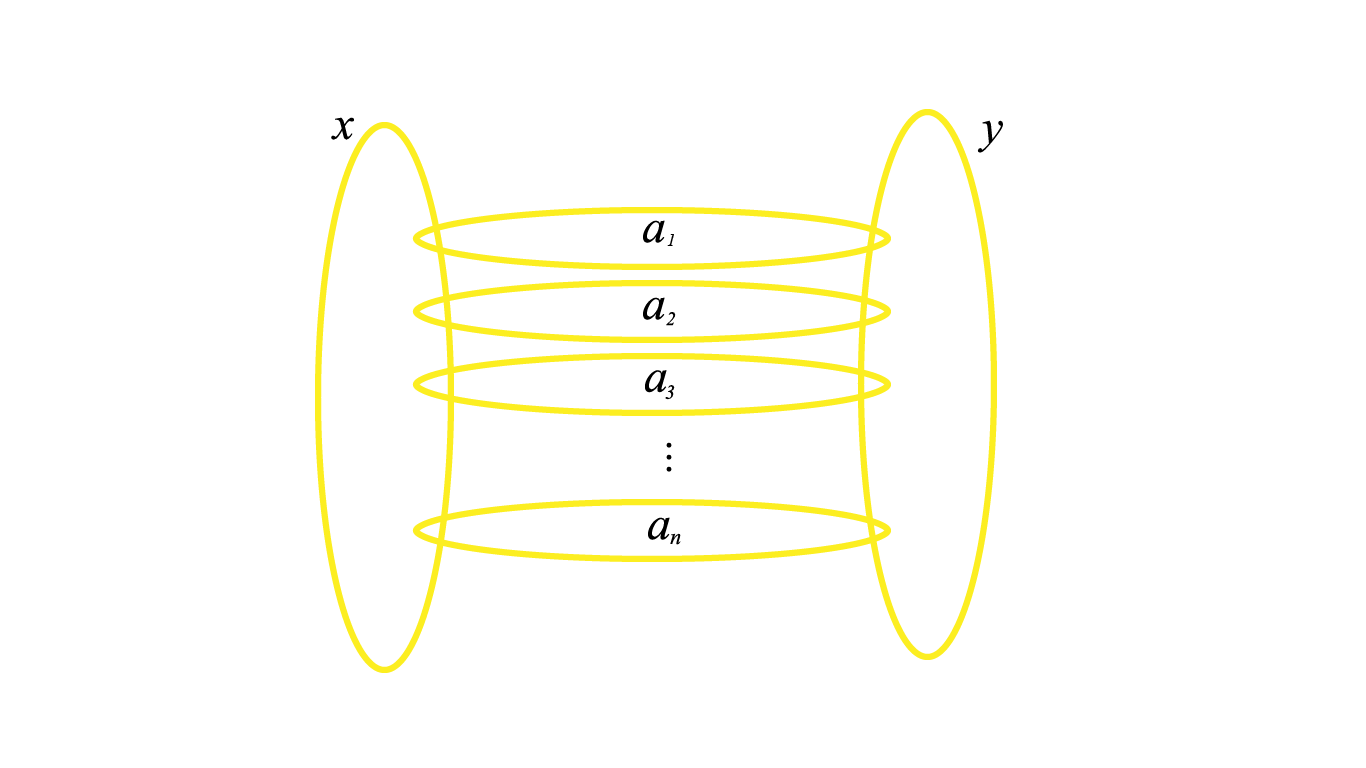
این زنجیر دو حلقه جدا از هم به ارزش $x$ و $y$ تومان دارد که با $n$ زنجیر کوچک‌تر و دو به دو جدا از هم به یکدیگر متصل شده‌اند. ارزش حلقه‌ی کوچک‌ها به ترتیب $a_1, a_2, \dots, a_n,$ تومان است.

می‌خواهیم مقدارهای $x$ و $y$‌ و $a_1, a_2, \dots, a_n,$ را طوری تعیین کنیم که بتوانیم همه‌ی مبالغ $1$ تا $x + y + a_1 + \dots + a_n$ را پرداخت کنیم.

برای پرداخت اگر تصمیم بگیریم تعدادی از حلقه‌ها را بدهیم فرض کنید بقیه‌ی حلقه‌ها ناپدید می‌شوند و ما می‌توانیم حلقه‌های باقی‌مانده را پرداخت کنیم.

همچنین می‌خواهیم حلقه‌هایی که به یک نفر می‌دهیم باید همبند باشد یعنی به دو قسمت تبدیل نشود و حلقه‌ها تو در توی هم باشند. فرض کنید شکستن یا داخل هم کردن حلقه‌ها ممکن نیست.

از شما می‌خوهیم طوری عدد گذاری کنید که حداکثر مبلغ ممکن را پرداخت کنیم.

برای بهتر فهمیدن خواسته‌ی سوال، مثال‌ها را ببیند.

ورودی

در تنها سطر ورودی، عدد صحیح و مثبت $n$ داده می‌شود. $$2 \leq n \leq 50 $$

خروجی

در سطر اول خروجی، دو مقدار طبیعی $x$ و $y$ را چاپ کنید. در سطر دوم خروجی، $n$ عدد طبیعی $a_1, a_2, \dots, a_n,$ با فاصله از هم چاپ کنید.

$$1 \leq x, y, a_1, a_2, \dots, a_n \leq 10^{18}$$

اگر چند جواب مختلف وجود دارد یکی را به دلخواه چاپ کنید.

مثال‌ها

ورودی نمونه ۱

2

خروجی نمونه ۱

1 2
3 7

اگر عددگذاری را مانند شکل زیر انجام دهیم همه‌ی مبالغ از ۱ تا ۱۳ تومان قابل پرداخت با تعدادی حلقه‌ی متصل به‌هم است.

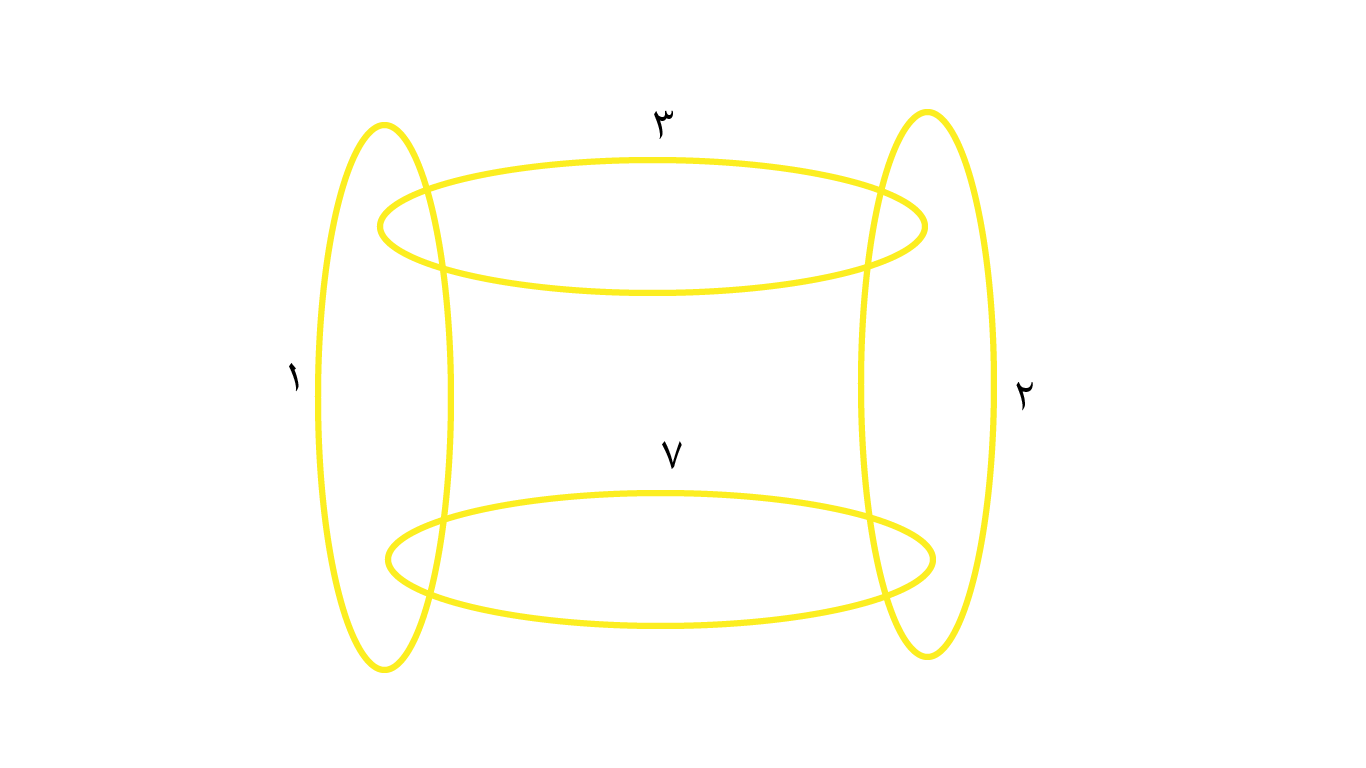
• برای پرداخت ۱ تومان حلقه‌ی ۱ را می‌دهیم.
• برای پرداخت ۲ تومان حلقه‌ی ۲ را می‌دهیم.
• برای پرداخت ۳ تومان حلقه‌ی ۳ را می‌دهیم.
• برای پرداخت ۴ تومان حلقه‌های ۱ و ۳ را می‌دهیم.
• برای پرداخت ۵ تومان حلقه‌های ۲ و ۳ را می‌دهیم.
• برای پرداخت ۶ تومان حلقه‌های ۱، ۲ و ۳ را می‌دهیم.
• برای پرداخت ۷ تومان حلقه‌ی ۷ را می‌دهیم.
• برای پرداخت ۸ تومان حلقه‌های ۱ و ۷ را می‌دهیم.
• برای پرداخت ۹ تومان حلقه‌های ۲ و ۷ را می‌دهیم.
• برای پرداخت ۱۰ تومان حلقه‌های ۱، ۲ و ۷ را می‌دهیم.
• برای پرداخت ۱۱ تومان حلقه‌های ۱، ۳ و ۷ را می‌دهیم.
• برای پرداخت ۱۲ تومان حلقه‌های ۲، ۳ و ۷ را می‌دهیم.
• برای پرداخت ۱۳ تومان حلقه‌های ۱، ۲، ۳ و ۷ را می‌دهیم

همچنین ۱۳ بیشترین عددی است که می‌توانیم پرداخت کنیم.

توجه کنید برای پرداخت ۳ تومان نمی‌توانستیم حلقه‌ی ۱ و ۲ را بدهیم چون دو تکه می‌شود و شرط همبندی را ندارد.